一种深层过程神经网络及其在信号分类中的应用
2020-05-28刘晓宇武鲁许少华
刘晓宇 武鲁 许少华


摘 要:針对时变信号小样本集建模分类问题,提出一种深层多尺度径向基过程神经网络(DLMS-RBFPNN)。该模型由时变信号输入层、多尺度径向基核变换层、全连接层和感知机分类器构成。兼顾时变信号的频谱特征和分布形态的多样性,基于径向基过程神经网络,通过将不同宽度参数的Gauss核函数进行线性叠加,构成多尺度核,完成不同尺度上对过程信号形态特征的提取、辨识和相似性度量。通过在径向基核函数层之上叠加全连接层和分类器,实现时变信号不同尺度特征的融合和分类。DLMS-RBFPNN具有较少的模型参数,适用于小样本集建模,在机制上可提高对时变信号过程细节特征和趋势特征的辨识及记忆能力。在分析DLMS-RBFPNN性质的基础上,建立一种基于动态聚类算法的核中心函数确定方法以及基于PSO的模型参数优化求解算法。以旋转机械基于示功图信号的故障诊断为例进行实验,结果验证了模型和算法的有效性。
关键词:动态模式识别; 多尺度核函数; 径向基过程神经网络; 深层结构; 优化算法
DOI:10. 11907/rjdk. 192486
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2020)003-0060-05
A Deep Layer Process Neural Network and Its Application in Signal Classification
LIU Xiao-yu1, WU Lu1,2, XU Shao-hua1
(1.School of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China;
2.Shandong Computing Center, Jinan 250014, China)
Abstract: Aiming at the modeling classification problem of small sample set of time-varying signals, this paper proposes a model based on deep layer multi-scale radial basis function process neural network (DLMS-RBFPNN). The model consists of a time-varying signal input layer, a multi-scale radial basis function kernel transform layer, a fully connected layer and a perceptron classifier. Taking into account the diversity of the spectral characteristics and distribution patterns of time-varying signals, the radial basis process neural network and the Gauss kernel function with different width parameters are linearly superposed to form a multi-scale kernel and complete the identification and similarity measure of process signal morphological features at different scales. The model realizes the fusion and classification of different scale features of time-varying signals, by superposing fully connected layers and classifiers on the radial basis kernel function layer. DLMS-RBFPNN has fewer model parameters and is suitable for small sample set modeling. It can improve the recognition and memory ability of time-varying signal process features. This paper analyzes the nature of the DLMS-RBFPNN model, proposes the center determination method of kernel function based on dynamic clustering, and constructs the model parameter optimization algorithm based on PSO. The fault diagnosis of rotating machinery based on dynamometer diagram is taken as an example. The actual data processing results show the effectiveness of the model and algorithm.
Key Words: dynamic pattern recognition; multi-scale kernel function; radial basis function process neural network; deep structure; optimization algorithm
0 引言
非线性时变信号是一种频率和幅值随时间变化的多成分信号,具有非线性、非平稳等特性,往往呈现多峰、伸缩、漂移、含噪声等特征,对时间变化依赖程度高,特别是多变量系统多个信号的组合过程特征呈现出高度的复杂性[1],其分类处理一直是信号分析与人工智能研究领域的一个重要课题[2]。
人工神经网络是目前信号处理和分析中一种常用而有效的方法[3]。随着深度学习理论的发展,一些新的可用于时变信号分析的神经网络模型不断被提出,例如,深度卷积神经网络[4-6]、深度递归网络[7]、深度循环网络[8-9]、Markov链[10]等,在机制上可有效实现对时间序列信号的分类分析,并取得了良好的应用效果。
在实际中,由于一些动态系统的过程事件不可重复、一些案例事件发生较少、样本采样代价高昂等因素,难以获得大规模完备的数据集,这给信号系统的建模分析带来许多困难[11]。针对小样本集建模问题,许多学者展开了相关研究,目前主要方法有基于泊松分布模型的朴素贝叶斯分类方法[12]、鲁棒单隐层前馈神经网络(SLFN)与极限学习理论相结合的分类方法[13]、数据增强与迁移训练结合的小样本数据处理方法[14]、支持向量机分类方法[15]、全局特征及弱尺度融合策略[16]等。但以上方法都面向特定问题,普适性较差。
基于核函数方法的信号分析和数据特征的多尺度表示是目前信号处理的一种有效方法[17-18]。由于模型参数少,因此在机制上适用于小样本集的建模分析。2006年,Roland Opfer19]提出了多尺度核函数的概念,并采用小波和移位变量技术构造新的核函数类;2014年,Zhang等[20]提出应用于短时说话识别的多尺度核函数,构造一系列不同尺度的内核,通过多核学习(MKL)优化方法组合,增强了模型的鲁棒性和可扩展性;2016年,胡站伟等[21]提出基于多尺度的类指数分布核函数(ELK),对局部特征有很好的捕捉优势;2017年,RABIN N等[22]提出一种用于数据嵌入和扩展的高阶核,这些核构成尺度高斯函数的线性组合,对特征捕获更加精确。
径向基过程神经网络(Radial Basis Function Process Neural Network,RBFPNN)[23]是近几年提出的一种新型动态神经网络模型,与传统径向基神经网络的不同之处在于其输入可以是连续时间函数,通过自适应提取时间输入函数的过程形态特征,并将多个特征加以组合,形成类别输出。将RBFPNN模型用于时变信号分类问题,可以直接输入连续信号而无需预先提取信号的形态和幅值特征,并且能够通过典型样本的学习直接获得信号与模式类别之间的对应关系,同时,RBFPNN模型参数少,因此,在机制上对于小样本集建模分类问题具有良好的适应性。
在实际工程中,非线性系统动态样本的模式特征变化相比数值向量样本要复杂得多,时变采样信号常常受随机因素、噪声信号以及一些不确知因素的影响[24],模态特征多变且不规则,包含的特征信息容量大。径向基神经网络的核函数形式及其核参数选取对于動态信号分类或预测结果有着十分重要的影响,在目前研究中,RBFPNN的核函数一般取为Gauss函数,其性质参数为核宽度。虽然在理论上可由大数定律证明Gauss函数对于各类数据的分析问题具有普适性[25],但对于一些复杂的信号处理问题,在一个尺度上难以区分时间输入信号细节特征与核中心函数的差异,致使分类结果出现偏差,特别是在不同类时间采样信号之间具有较强的相似性和多峰情况[26]。因此,需要改进RBFPNN模型对细节特征的辨识能力,以及对不同尺度特征的融合分析能力。在模型中引入不同尺度参数并增加网络深度,为问题的解决提供了一种有效方法。
笔者提出了一种深层多尺度径向基过程神经网络(Deep Layer Multi Scale RBFPNN,DLMS-RBFPNN)模型。通过将不同宽度参数的Gauss核进行线性叠加,以构成具有多尺度性质的核函数,提高对输入时变信号过程特征的表征和度量能力,使对时间信号细节特征的刻画在尺度选择上具有更好的完整性和灵活性,从而获取分类模型对过程信号特征的多分辨能力。通过在核函数层之上增加一个全连接层,则可实现对时变信号不同尺度特征的融合。DLMS-RBFPNN模型对于解决过程信号具有较强异构性、同类样本呈多模态变化的复杂时间信号分类问题,在信息处理机制上具有很好的适应性。文中分析了DLMS-RBFPNN的信息处理机制,给出了基于带动态惯性因子粒子群算法的模型参数优化学习方法。将其应用于基于振动检测信号的旋转机械故障诊断问题,取得了良好的应用效果。
1 径向基过程神经网络模型
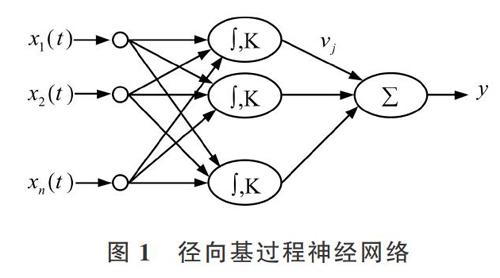
径向基过程神经网络[23]为三层结构模型,输入层有[n]个节点单元,完成时间过程信号向网络输入;中间径向基核函数层有[m]个节点单元;网络输出为隐层节点输出信号的线性加权和,其拓扑结构如图1所示。
图1中,[vj(j=1,2,?,m)]为输出层权系数,“∫”为时间聚合算子,[K(?,?)]为径向基核函数。
设时间信号输入区间为[[0,T]],[X(t)=(x1(t),][x2(t),?,][xn(t))]([t∈[0,T]])为网络输入函数, [Zj(t)]为第[j]个径向基过程神经元的核中心函数。若“∫”取为[[0,T]]上的积分,则RBFPNN输入输出之间的关系为:
式(1)中,[||?·||]为[(C[0,T])n]空间中的某一距离范数。
若径向基核取为Gauss函数:
[K(v)=exp(-v22σ2)],则式(1)可写为:
其中,[σ]为核宽度参数,描述样本的统计分布性质。径向基核具有数据结构的保持特性,即在特征映射空间中可保持原有数据体的结构和信息关联关系。
2 多尺度径向基过程神经网络
2.1 多尺度径向基核函数
Gauss核函数是目前广泛使用的一种核函数,其性质和映射关系由核中心函数及核宽度参数确定。对应第[j]个隐层单元,考虑[Lj]个宽度参数及核中心函数不同的Gauss函数。
其中,核宽度参数满足[σj1>?>σjL],[zjLj(t)]为第[j]个径向基核中对应[σjLj]细分类的核中心函数。
将上述核函数进行线性叠加,第[j]个隐层单元的多尺度核函数定义为:
式(3)中,[βl]([l=1,2,?,L])为加权系数,由训练集样本学习确定;[zj(t)=(zj1(t),zj2(t),?,zjLj(t))]。
核的本质是按照某种方式去度量数据体与数据体之间的特征相似性,时间信号样本[X(t)]与核中心函数[zj(t)]之间的过程特征相似度越高,即[x(t)-zj(t)]越小,则核函数输出值越大,对分类决策的作用就越显著。式(3)定义的关于核宽度参数的多尺度形式仍保留了径向基核函数的性质,使对时间信号细节特征的刻画在尺度选择上具有更好的完整性和灵活性,在机制上可改善RBFPNN对时变信号的辨识性质。
2.2 深层多尺度径向基过程神经网络
深层多尺度径向基过程神经网络(DLMS-RBFPNN)由时变信号输入层、多尺度径向基核函数层、全连接层和输出层构成。其结构如图2所示。图2中,[wij]为核函数层各节点与全连接层节点的连接权,[vj]为全连接层与输出层节点的连接权。以式(3)为第[j]个隐层单元的核函数,由图2可知,DLMS-RBFPNN输入输出之间的映射关系为:
式(4)中, [m]为径向基核函数隐层节点数,[K]为全连接层节点数。
对尺度不同的核函数进行线性加权组合,本质上是将过程信号特征细化,在多个不同宽度参数条件下,综合度量时变过程信号之间模态细节特征的相似性,降低机器模型的结构风险。同时,全连接层在同类样本细分特征组合的基础上,又进行了更高层次组合的特征组合,可提高对信号样本的抗噪声能力,实现对输入信号与核中心函数在细节特征上更为完整的相似性度量。
3 DLMS-RBFPNN优化求解
DLMS-RBFPNN的学习采用有监督的参数调整算法,可将训练集的样本标签数作为径向基隐层节点数,再利用动态聚类算法进行相同标签样本子集的细分类,以分类数和细分类中心函数作为多尺度核的[Lj]及细分核中心函数[zjl(t)],宽度参数[σjl]可由细分类样本广义方差或通过DLMS-RBFPNN整体参数调整确定。在式(4)表示的网络模型中,连接权系数[wij]、[vj] ([i=1,2,?,m;j=1,2,?,][K])和[βil]([l=1,2,?,L])通过PSO算法进行优化求解。
3.1 核中心函数及隐层节点数确定
采用广义欧式距离进行时间信号样本之间过程特征相似性度量,利用动态聚类算法确定DLMS-RBFPNN各隐层节点中细分类数[Lj]及细分核中心函数[zjl(t)]。
设函数[X(t)],[Y(t)][∈(C[0,T])n],定义[X(t)]、[Y(t)]在[[0,T]]上的相似系数:
其中,[
设第[j]类标签子集包含[Kj]个时间函数样本:{[X1j(t),X2j(t),?,XKjj(t)];[Xkj(t)∈][(C[0,T])n]}。设置3个聚类参数:初始分类数[H0]、样本相似系数阈值[θ]和类间距离阈值[R]。用式(5)定义的相似系数的倒数度量两个输入函数样本间的距离,以两类中两两输入函数样本间距离的最小值为类间距离,动态聚类算法步骤如下:
Step1:在样本集中,选取[H0]([H0][][K])个样本作为[H0]个模式类的代表,构成初始[H0]个类。
Step2:将样本集中其余函数样本依次计算与每个已有模式类代表之间的相似系数。若其中最大相似系数小于[θ],则以该样本为成员形成一个新类,并以其为该新类的代表,[H0]+1→[H0];若其中最大相似系数大于[θ],则将该函数归于相似系數最大的一类,并以该样本与原类代表样本的均值作为合并后新类的代表。
Step3:计算[H0]个类两两之间的类距离。若两个类的类间距离小于[R],则将这两个类合并,以两类类代表函数样本的均值作为新类的代表;若类间距离大于[R],则两个函数样本类不作改变。
Step4:执行上述步骤后,分类数可能改变,以新的分类个数替代[H0]。如果分类结果(包括分类个数和函数样本的具体分类)改变,则返回Step2继续执行;如果分类结果不再变化,则分类完成。
此时,得到的分类个数[H0]即可作为RBFPNN第[j]个隐层单元的细分节点数[Lj],子类聚类中心函数作为细分核中心函数[zjl(t)]。
3.2 基于PSO算法网络参数确定
考虑对DLMS-RBFPNN参数搜索范围的约束和全局优化性质,采用带动态惯性因子的 PSO 算法[27],实现核函数宽度参数[σ2jl]和权系数[wij] 、[vj]、[βjl][(j=1,2,?,L,][i=1,2,?,m;l=1,2,?,L)]的整体优化求解。
设在[n]维空间中,由[m]个粒子组成一个种群,其中第[i]个粒子的位置[Xi]、速度[Vi]、自身最优位置[Pi]及全局最优位置[Pg]分别为:[Xi=(xi1,xi2,?,xin)],[Vi=(vi1,vi2,?,vin)],[Pi=(pi1,pi2,?,pin)]和[Pg=(pg1,][pg2,?,][pgn)]。粒子状态更新策略为:
其中,[w(s)]是动态惯性因子,采用线性递减权重策略进行设置:[w(s)=wmax-(wmax-wmin)Tmax?s],[s]为迭代次数,[Tmax]为最大迭代次数,[wmax]和[wmin]分别为最大惯性权重及最小惯性权重;[c1]、[c2]是常数;[r1]、[r2]为[[0,1]]之间的随机数。对种群中每个粒子用式(6)、式(7)进行循环迭代,实现整个种群向全局最优解的逐步逼近。PSO算法具体实施步骤如下:
Step1:确定种群规模[N],随机生成初始种群[G],采用十进制数对染色体进行编码,每条染色体上基因数为待优化的变量个数;设置最大迭代代数,误差精度[ε]。
Step2:构造适应度函数。由于训练为目标函数极小值优化问题,适应度函数取为[fit=e-E]。
Step3:PSO初始化, [w(s)]计算式中的[wmin]取0.4, [wmax]取0.9。
Step4:按照式(6)和式(7)进行循环迭代,若满足终止条件,则保存最优解停机。
4 实验分析
旋转机械是以转子及其它回转部件作为工作主体的机械设备,运行中的常见故障主要包括:由转子质量偏心和转子部件缺损引起的转子不平衡,转子之间的轴线由于安装误差、承载后变形等造成的转子不对中,以及转子与静止部件之间的摩擦而引发的转子碰磨等。利用机械振动检测信号进行旋转设备故障诊断,由于不同故障类型对应不同的时域波形信号,因此可通过对采样区间内连续信号波形的识别实现故障诊断。旋转机械运动呈周期性,故可将机械的一个旋转周期作为采样区间,将一个周期内的信号连续变化过程作为一个样本。旋转机械工作状态主要分为正常运转、转子不平衡、转子不对中和转子碰磨共4种模式,典型信号曲线如图3所示。
从某机械装备质量检测中心获取旋转机械检测样本350个,其中3类故障样本各100,运行正常样本50个。按比例分别选取70条转子不平衡、75条转子不对中、70条转子碰磨和35条正常共250条信号曲线组成训练样本集,测试集由其余100个样本组成。由于设备检测信号为离散采样数据,采用Legendre多项式函数系进行函数拟合,基函数个数[L]为5时满足精度0.05的拟合要求。以式(4)定义的深层多尺度RBFPNN作為故障自动诊断器,以一个周期内的连续变化信号作为网络输入,输出为机械工作状态。DLMS-BRFPNN网络结构参数选择如下:1个时间信号输入节点,20个径向基核隐层节点,40个全连接层节点,1个故障模式输出节点。转子不平衡情况输出对应0.25,转子不对中情况对应0.50,转子碰磨情况对应0.75,正常工作状态对应1.0。考虑同类故障信号样本模态特征的差异性,采用动态聚类算法分别对3种故障样本集进行类内聚类,相似性阈值[θ]取0.75。聚类结果为转子不平衡细分类数[L1]=6,转子不对中细分类数[L2=]6,转子碰磨[L3=5],正常情况为[L4=]3。以各细分类中心函数为[zjl(t)]([l=Lj;j=1,2,3,4]),细分类宽度参数采用广义方差计算。
其中,[Kjl]为细分类中的样本数,[xjlk(t)]为细分类中第[k]个信号样本。
采用PSO算法对模型参数[wij,vj,βjt]([l=Lj;j=1,2,][3,4])进行整体优化求解。设置种群规模[G]=20,最大迭代次数[M]=1 000,学习精度[ε]=0.05。PSO算法参数取[c1=0.3],[c2=0.8];[r1=0.45],[r2=0.83]。作为对比,分别采用可直接输入时间信号进行判别的基于函数正交基展开的双隐层过程神经网络模型[28],网络结构为1-10-20-1,正交基取为5项Legendre多项式函数基;RBFPNN模型[23],网络结构为1-20-1。3种模型采用相同的训练集、测试集进行训练和测试,以准确率、召回率、精确率和F1等4项指标对模型性质进行评价,结果见表1。本文方法具体分类正确率如表2所示(混淆矩阵)。
实验结果表明,本文建立的深层多尺度径向基过程神经网络诊断模型相比于PNN和RBFPNN诊断模型,在旋转机械故障辨识性能指标上有较大提高。这是由于在核函数构造中,多尺度核及全连接层的特征融合改善了诊断模型对复杂时间信号过程特征的辨识和记忆性质;在类特征组合的基础上,又进行了更高层次组合的特征组合,可实现对输入信号与核中心函数在细节特征上的相似性度量,达到了比较理想的诊断结果。
5 结语
本文提出了适用于小样本集建模分类的一种深层多尺度径向基过程神经网络模型和算法。模型从结构上改善了对时变信号形态特征之间的相似性度量和记忆性质,可提高RBFPNN对动态样本复杂模态特征多样性和复杂性的辨识能力,以及分类模型对时变信号过程细节特征的捕获能力。但由于多尺度组合的核函数较大增加了尺度等相关参数,全连接层增加了连接权参数,使得网络计算复杂度提高。因此,研究效率更高、更优化的学习算法,是需要进一步研究的重要课题。
参考文献:
[1]奥本海姆,谢弗,巴克,等. 离散时间信号处理[M]. 第2版. 西安:西安交通大学出版社, 2001.
[2]祁才君. 数字信号处理技术的算法分析与应用[M]. 第1版. 北京:机械工业出版社,2005.
[3]徐百家,王亚清. 人工神经网络用于时域信号识别[J]. 信息与控制,1996,25(3):187-192.
[4]唐志川,张克俊. 基于深度卷积神经网络的运动想象分类及其在脑控外骨骼中的应用[J]. 计算机学报,2017,40(6):1367-1378.
[5]袁文浩,孙文珠. 利用深度卷积神经网络提高未知噪声下的语音增强性能[J]. 自动化学报,2018,44(4):751-759.
[6]ACHARYA U,RAJENDRA F. Application of deep convolutional neural network for automated detection of myocardial infarction using ECG signals[J]. Information Sciences,2017,415-416:190-198.
[7]TAI Y,YANG J,LIU X M,et al. Image Super-Resolution via deep recursive residual network[C]. Honolulu:IEEE Conference on Computer Vision and Pattern Recognition,2017:1-24.
[8]SHI J,WEN H,ZHANG Y Z,et al. Deep recurrent neural network reveals a hierarchy of process memory during dynamic natural vision[J]. Human Brain Mapping,2018,39(5):2269-2282.
[9]VIDYARATNE L,GLANDON A,ALAM M,et al. Deep recurrent neural network for seizure detection[C]. Vancouver:2016 International Joint Conference on Neural Networks (IJCNN),2016.
[10]朱勇剛,李永贵. 噪声功率时变的瑞利慢衰落信道有限状态Markov模型[J]. 信号处理,2013,29(1):135-141.
[11]杨智勇,许爱强. 基于多信号模型的系统测试性建模与分析[J]. 工程设计学报,2007,14(5):364-368.
[12]邸若海,高晓光. 小数据集BN建模方法及其在威胁评估中的应用[J]. 电子学报,2016,6(44):1504-1511.
[13]张荣,邓赵红. 针对小样本数据集的鲁棒单隐层前馈网络建模方法[J]. 控制与决策,2012,27(9):1308-1319.
[14]段萌,王功鹏. 基于卷积神经网络的小样本图像识别方法[J]. 计算机工程与设计,2018,39(1):224-229.
[15]刘占生,窦唯. 基于主元-双谱支持向量机的旋转机械故障诊断方法[J]振动与冲击,2007,26(12):23-27.
[16]黄永明,章国宝. 全局特征及弱尺度融合策略的小样本语音情感识别[J]. 声学学报,2012,37(3):330-338.
[17]满瑞君,梁雪春. 基于多尺度小波支持向量机的交通流预测[J]. 计算机仿真,2013,30(11):156-159.
[18]李秀梅,杨国青. 几种时频分析方法的性能比较[J]. 计算机仿真,2015,32(3):220-224.
[19]ROLAND O. Multiscale kernels[J]. Advances in Computational Mathematics, 2006.
[20]ZHANG W,ZHAO J,ZHANG W L,et al. Multi-scale kernels for short utterance speaker recognition[C].9th International Symposium,Singapore,Chinese Spoken Language Processing,2014:414-417.
[21]胡站伟,焦立国. 基于多尺度重采样思想的类指数核函数构造[J]. 电子与信息学报,2016,38(7):1689-1695.
[22]RABIN N,FISHELOV D.Multi-scale kernels for Nystr?m based extension schemes[J]. Applied Mathematics and Computation,2018,319:165-177.
[23]许少华,何新贵. 径向基过程神经元网络及其应用研究[J]. 北京航空航天大学学报,2004,30(1):14-17.
[24]WANG J,XU G,ZHANG Q,et al. Application of improved morphological filter to the extraction of impulsive attenuation signals[J]. Mechanical Systems and Signal Processing, 2009, 23(2): 236-245.
[25]GU D B,HU H S. Spatial Gaussian process regression with mobile sensor networks[J]. IEEE Transactions on Neural Networks and Learning Systems,2012(23):1279-1290.
[26]汪洪桥,孙富春. 多核学习方法[J]. 自动化学报,2010,36(8):1037-1050.
[27]EBERHART R C,SHI Y.Comparing inertia weights and constriction factors in particle swarm optimization[C]. 2000 Congress on Evolutionary Computation,2000:84-88.
[28]许少华,何新贵. 基于基函数展开的双隐层过程神经元网络及其应用[J]. 控制与决策,2004,19(1):36-39.
(责任编辑:孙 娟)
收稿日期:2019-11-14
作者简介:刘晓宇(1994-),女,山东科技大学计算机科学与工程学院硕士研究生,研究方向为大数据分析、人工智能;武鲁(1982-),男,山东科技大学计算机科学与工程学院博士研究生,山东省计算中心研究员,研究方向为大数据分析、人工智能;许少华(1962-),男,博士,山东科技大学计算机科学与工程学院教授、博士生导师,研究方向为大数据分析、智能信息处理。本文通讯作者:许少华。
