考虑电池能效的电网侧电化学储能电站最优功率控制策略研究

冯力勇，张云

（长园深瑞继保自动化有限公司，广东深圳518057）

0 引言

随着可再生能源发电量占整个电力系统发电量的比重不断提高，尤其是风电、光伏所具有的波动性、随机性、难预测等特点，给电力系统稳定运行与控制带来巨大挑战。储能系统既可作为电源又可作为负荷，灵活的双向互动性能将使其在可再生能源发电消纳中发挥重要作用［1-3］。另外，随着国内特高压的建设，在特高压直流紧急闭锁的情况下，会在短时间内造成区域电网频率波动，需要地区电网具有紧急切负荷以及调频的能力［4-10］。储能系统在调频和紧急响应方面具有重要价值，特别是电化学储能，其变流器具有响应速度快，精度高的特点，相比其他电源和负荷，具有更优良的调节控制性能。

近年来，我国电网侧储能发展迅速，其中江苏、河南、湖南、浙江等地陆续投资建设了一批电网侧电化学储能电站，这些电站可以为电网运行提供调峰、调频、备用、黑启动、需求侧响应等多种服务，提升电网运行效率，缓解地区供电负荷压力［11-19］。

目前电网侧电化学储能电站主要受调度机构控制，运行过程中，储能电站与调度系统通过最大可充放电进行功率约束，调度系统下发自动发电控制（AGC）目标值给储能电站站端能量管理系统（EMS），由其进行全站功率分配和下发。站端EMS在统计全站最大可充放电功率时，需要考虑各电池组和变流器的故障和告警信息，但是目前不考虑电池组的能效特性。由于电化学储能电站电池数量多，电池必然存在一致性偏差，导致在长期统一充放电过程中，各部分电池荷电状态（SOC）和能效发生较大偏差，部分运行工况下会出现全站损耗较大、效率较低的情况，既降低了电化学储能电站的经济效益，也降低了电池寿命和可运行时间。

为了提升电化学储能电站的运行效率和经济性，本文针对目前采用的磷酸铁锂电池的电网侧储能不同应用场景进行分析，建立储能电站优化运行控制模型并求解，模型以全站输出功率以及综合能效为目标，以储能电池、电池管理系统（BMS）、储能变流器（PCS）、站端设备及大电网运行工况为约束。

1 考虑电池能效的储能电站运行模型

1.1 磷酸铁锂电池的动态能效特性

电化学储能的能效特性相比其他储能有所不同，不同材质的电化学储能能效特性也不同。本文以目前电网侧储能电站采用的主流电化学储能介质磷酸铁锂为例。

放电环节中，磷酸铁锂电池在合理放电深度范围内电压基本不变，效率随着充放电电流增大会有不同程度地下降。根据文献［20］的研究结果，磷酸铁锂电池电压与SOC的关系，能效与充放电电流及SOC的关系，可以得出磷酸铁锂电池的放电效率曲线，如图1所示。由图1可知，磷酸铁锂电池的放电效率近似线性下降。本文将其近似线性化处理。充电阶段与放电阶段原理相同，可以统一处理。

1.2 电化学储能电站运行目标

电网侧电化学储能电站优化运行的目标为全站能效最大，经济性最高，这是优化目标，可以等效为站端储能充放电损耗最小，即Ploss最小。

假定储能电站有i台PCS，每台PCS的充放电功率为Pi，PCS在该充放电功率下对应的能效为ηi，则该台PCS的充放电功率损耗为。

综上所述，构造电网侧电化学储能电站运行的目标函数F。

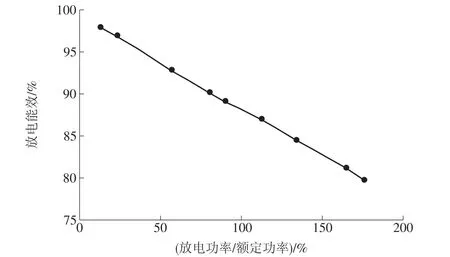
图1 磷酸铁锂电池放电能效与放电功率/额定功率比值的关系曲线Fig.1 Relationship between LiFePO4battery discharge efficiency and the ratio of discharge efficiency to rated power

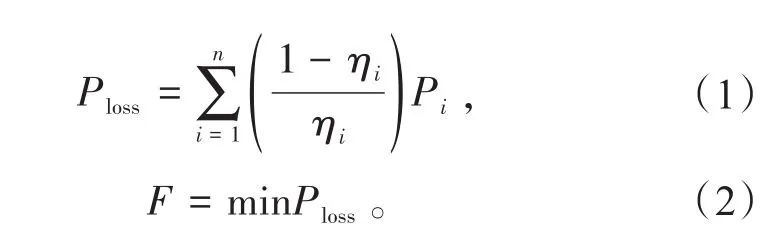
将1.1节中磷酸铁锂电池的能效曲线近似线性化，构造能效与充放电功率的关系为

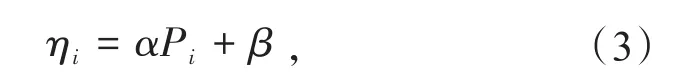
式中：α，β为磷酸铁锂电池的自特性，与储能电站运行方式无关，可以认为是一个常数，其中能效范围ηi∈ (0，1)。将式（3）代入式（1），可以得到：

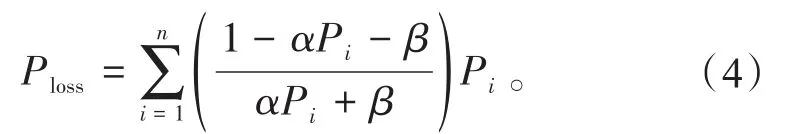
1.3 储能电站运行需求和约束

（1）满足调度功率指令需求，包括调度系统下发的实时AGC指令或计划曲线，这是主要优化目标。功率目标为

（2）满足每台PCS的运行工况和最大可充放电功率约束。

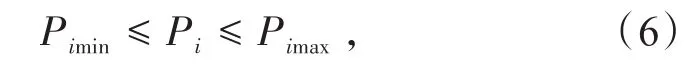
式中：Pimin和Pimax由PCS运行状态以及BMS运行状态综合评估得出，该数据一般由PCS上送站端EMS。

结合式（4）和式（5），可以得出

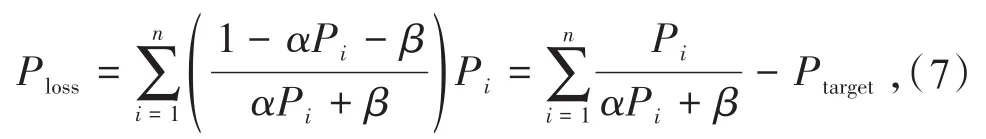
由于Ptarget是常数，因此目标函数可以转化为

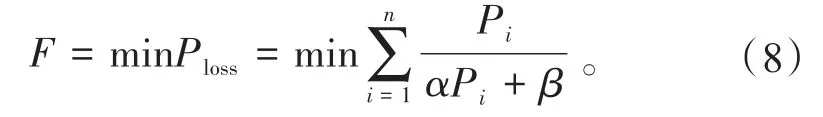
上述模型约束条件已线性化，目标函数为功率变量定义域上的凸函数，变量为连续型变量，对于非线性最优化问题，可以采用凸规划进行求解。对于正常运行工况下，储能单元没有限制功率运行，可以采用Jensen不等式进行简化计算。

若f（x）是区间（a，b）上的凸函数，则对任意的x1，x2，x3，…，xn∈ (a，b)，有不等式

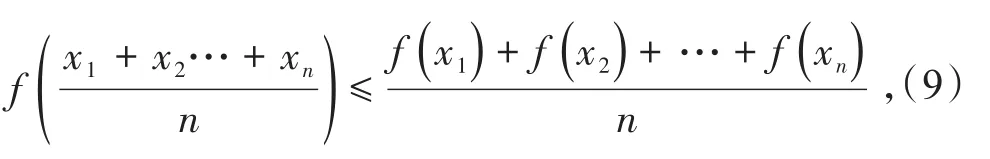
当且仅当x1=x2=x3=…=xn时等号成立。

由式（8）和（9）可以推导出

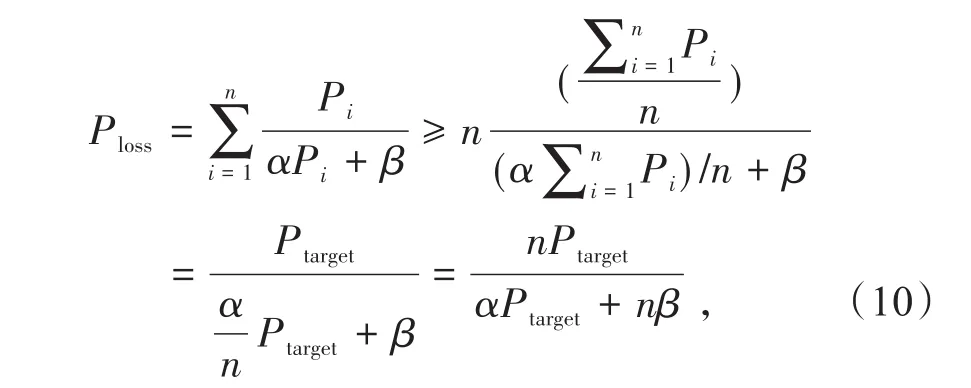
此时，P1=P2=…=Pn，即全站功率平均分配。

对于功率限制的工况，比如部分PCS告警或者BMS告警，平均分配越过了功率允许值，则需要采用凸规划进行求解。下文将基于算例仿真计算，对比多种运行场景下，常数能效和动态能效对储能电站功率控制的影响。

2 算例

以某5 MW/10 MW·h（即额定功率PN为5 MW，额定电池容量为10 MW·h）电网侧储能电站为例，该电站共配置10台PCS，每台PCS容量500 kW，假设充放电SOC区间为［10，90］。目前电网侧储能电站的充放电策略主要有2种，一种是根据每台PCS当前最大可充放电功率进行等比例分配（以下简称最大可充放电功率等比例算法），另一种是根据每台PCS关联的电池单元SOC进行SOC比例分配（以下简称SOC比例分配算法）。这2种方式均没有考虑到电池能效问题。

下面将对不同运行工况及不同功率目标值情况下，本文及上述2种方式的特点进行对比分析。

2.1 SOC不一致充放电工况

正常工况下，如果每台PCS的运行状态均一样，不管采用哪种分配方法，功率控制结果均一致。在电池堆SOC不一致，并且最大可充放电功率一致的情况下，对每种策略进行求解分析，结果见表1。

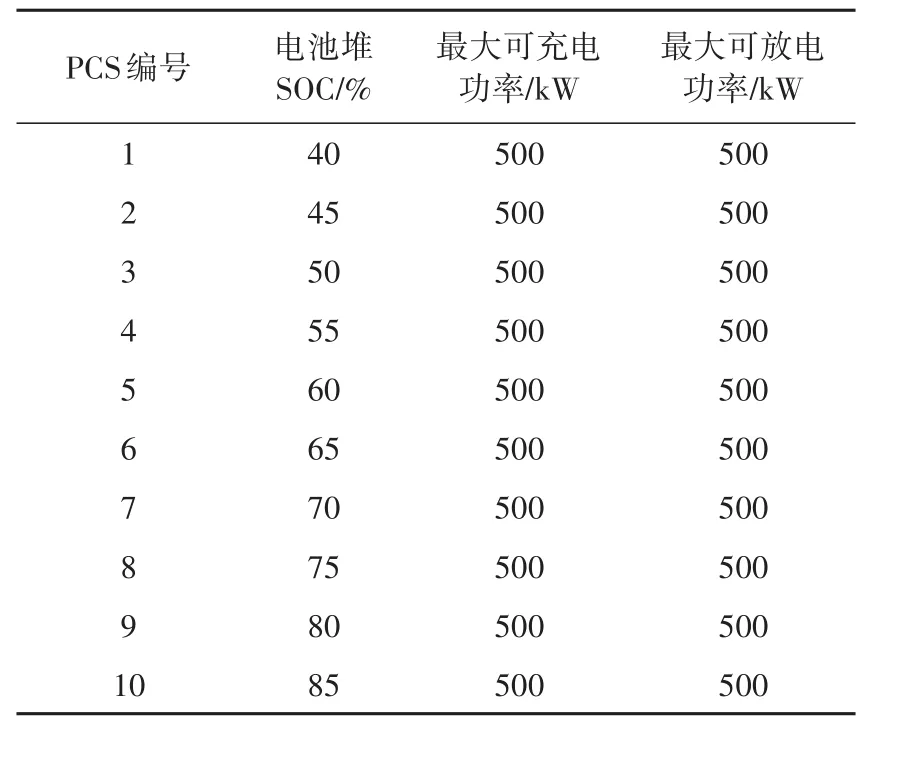
表1 仅电池堆SOC不一致的工况Tab.1 Working conditions with different SOC

根据上述工况，分别对 0.2PN，0.5PN，0.8PN，PN放电进行计算，得出相应指标见表2（修改前）。

由仿真计算结果可以看出，在电池堆SOC有偏差的情况下，基于SOC的比例分配方法能效偏低，但是策略可持续时间相比其他2种方法会增加很多。在接近额定功率充放电的情况下，各种算法形成的策略性能偏差较小。任何工况下，本文所提的方法均是能效最优的算法。

2.2 SOC不一致且功率限制工况

在电池堆SOC不一致且功率限制的情况下，对每种策略进行求解分析，结果见表3。

表2 3种算法的综合特性比较Tab.2 Comparison of three calculation methods

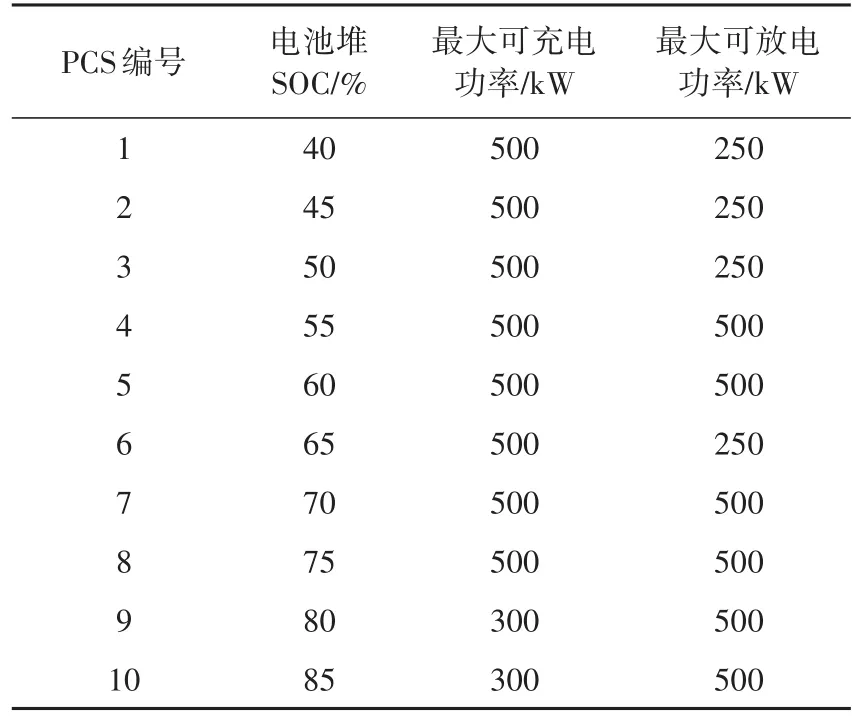
表3 SOC不一致且功率限制工况Tab.3 Working conditions with different SOC and power limit

对于限制功率输出的情况，电化学储能电站上送调度系统的最大可充放电功率会作相应调整。对于表3中的工况，最大可放电功率为0.8PN。此时电化学储能电站不具备PN输出能力，将测试用例修改为 0.7PN。分别对 0.2PN，0.5PN，0.8PN，0.7PN放电进行计算，得出相应的指标见表2（修改后）。

由表2仿真计算结果可以看出，在有PCS功率限制的情况下，采用SOC比例分配方法在能效方面比最大功率比例分配方法更好，持续时间最长。本文方法在能效方面最优，但是持续时间最短。因此目前储能电站的实时控制算法各有特点，没有哪一种方法在各方面均是最优。这就需要针对不同的应用场景，进行分析考虑。

3 多场景下储能电站运行控制策略分析

对于电网侧储能电站，响应调度指令作为主要目标，在满足该目标的基础上，针对不同的应用场景，还有不同的次要目标，对目前电网侧储能电站主要工作的几类场景进行分析。

3.1 调峰

对于调峰场景的应用需求，主要需要功率稳定输出和放电时间满足要求，因此，在功率满足调度需求时，应尽可能使功率稳定时间最长。根据本文分析，宜采用SOC比例分配的运行控制方式。

3.2 调频

储能电站参与调频，需要频繁进行浅充浅放操作，对于功率的持续时间要求不高，但是要求最大可充放电功率较大，从而提升调频的性能指标。在功率满足调频需求的情况下，次要优化目标是使全站的SOC维持在中间区域。根据本文分析，宜采用SOC比例分配的运行控制方式。

3.3 源网荷紧急响应

源网荷紧急响应需求，要求每台PCS按照最大功率进行放电，这时不需要EMS进行控制，因此这里不予分析。

3.4 源网荷经济运行

源网荷紧急响应后转经济运行时，需要按照储能电站本身能力进行功率输出，这时需要EMS执行最优经济运行策略。此时需要考虑电站经济效益指标，从而最大化电站运行效益。根据本文算法对比，宜采用最优能效的运行控制方式。

4 结论

对于电网侧储能电站的运行控制，本文重点分析了基于磷酸铁锂电池能效特性的电网侧电化学储能电站的最优充放电策略，并且对比现有的充放电策略，针对不同的工况和应用场景进行分析，得出结论，电网侧储能电站的最优运行控制方式应该随着场景变化而改变，单一策略不能满足所有的场景需求。目前电网侧储能电站运行考核评价指标尚未明确，各项标准尚不健全，电网侧储能电站的运行控制，尚有很多值得挖掘提升的空间。