基于多楔现象的微孔端面机械密封泄漏率分析及孔形设计

2020-05-28陈胡炜吉华冯东林李倩陈志

化工学报 2020年4期

陈胡炜，吉华，冯东林，李倩，陈志

（四川大学化学工程学院，四川成都610065）

引言

在机械密封端面加工微孔，能够减小摩擦和泄漏，提高液膜承载力[1-2]。微孔的形状对密封性能有较大的影响，早期的研究主要集中在圆形微孔[3-6]，近年来，椭圆形、菱形、矩形、三角形等规则方向性微孔[7-12]以及一些非规则形状的微孔[13-16]也得到了一定的研究。目前微孔形状的设计多基于试错法[7,17]和基于优化算法的设计法[13-16]，较少涉及密封机理。

对表面织构工作机理的理解是表面织构设计的基础，为了能够设计有效的表面织构，需要根据应用场合对表面织构的工作机理进行研究，利用机理来指导表面织构的设计[18-19]。因此，为了设计出能够改善密封泄漏性能的微孔形状，一些关于密封泄漏机理的研究得到了开展。彭旭东团队[8,20]对椭圆形、菱形、矩形、等腰三角形等方向性微孔进行了研究，对方向性微孔的泄漏机理进行了解释，认为反向泵送是方向性微孔减少密封泄漏率的主要原因，并将反向泵送的机理概括为“低压区的吸收，方向性微孔的导流，高压区的阻碍与释放”。吉华等[21-22]对椭圆形微孔的回吸现象进行了研究，由于低压区压力低于密封间隙流体出口截面处压力，形成的压差产生了回吸现象，可以利用微孔的回吸现象来控制密封的泄漏率。张科等[23]利用椭圆沿速度方向的几何收敛点建立了椭圆形微孔几何特性与泄漏率的联系，通过几何收敛点可以近似确定高低压区的分布，当高压区靠近泄漏出口时，泄漏率大；当高压区远离泄漏出口时，泄漏率小。

在流体动压润滑领域，1886 年楔形结构对压力分布的影响被首次提出[24-26]，当流体流经收敛性楔时将产生正压力，而流体流经发散性楔时将产生负压力。正是这两种楔的差异，微孔能够改变机械密封的性能。因此，吉华等[27]结合楔效应理论与压力分布云图分析了等边三角形微孔各楔的性质，提出了多楔现象，即等边三角形微孔沿流体流动方向会产生三个性质不同的楔，各楔的性质与强度随方向角的变化而变化，多楔现象改变了压力分布，并进一步影响到泄漏性能。

本文针对微孔端面液膜机械密封，在等边三角形微孔多楔现象研究的基础上，将多楔现象的分析方法拓展到椭圆形、菱形、矩形、等腰三角形四种方向性微孔，通过多楔现象解释了四种方向性微孔的几何特性与泄漏率的关系；将对多楔现象的理解，应用到微孔的形状设计中，以此来减小机械密封的泄漏率。

1 计算模型

1.1 几何模型

图1（a）为微孔分布示意图，其中密封环内半径ri=24 mm，外半径ro=34 mm。微孔沿径向呈放射状、周期性均匀分布，图1（b）为其中任意一个周期，每个周期均匀分布10 个微孔单元，共150 个周期。图1（c）白色部分表示任意一个微孔端面法向的间隙流体，h0表示液膜厚度，hp表示微孔深度。图1（d）为不同形状的方向性微孔的长轴、短轴和方向角的示意图，微孔长轴的长度为2a，短轴的长度为2b，不同形状的微孔之间长轴相等。方向角α为长轴与密封环旋转线速度u的逆时针夹角，α∈[0°,360°]。其中E表示椭圆形微孔，T 表示等腰三角形微孔，D 表示菱形微孔，R 表示矩形微孔。图1 中微孔位于静环表面，动环转速为n。

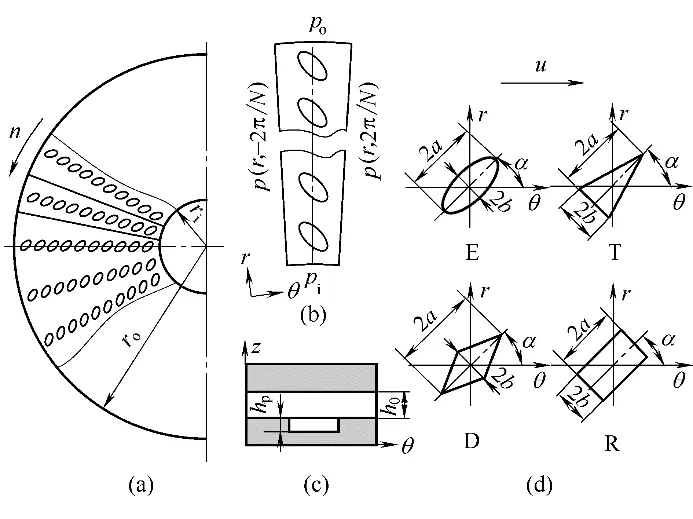
图1 微孔分布和计算域Fig.1 Micro-dimples distribution and calculation domain

采用UG 软件建立了一个周期的密封间隙流体的三维模型，使用Gambit 软件进行网格划分，在Fluent 软件中进行数值计算，其收敛判断准则为：各个方向的速度残差小于10-3，进出口质量流量误差小于1%。

计算参数如表1 所示。微孔面积比Sp是所有微孔的总面积与密封端面的面积的比值。在本研究中，密封端面上所有微孔的面积和长轴2a 均相等，在设计过程中利用微孔的面积和长轴2a 倒推计算微孔的短轴2b，短轴2b 保留小数点后四位数字，最终椭圆形、菱形、矩形和等腰三角形微孔的面积比分别为19.998%、20.001%、20.001%和20.001%，均在20%左右。

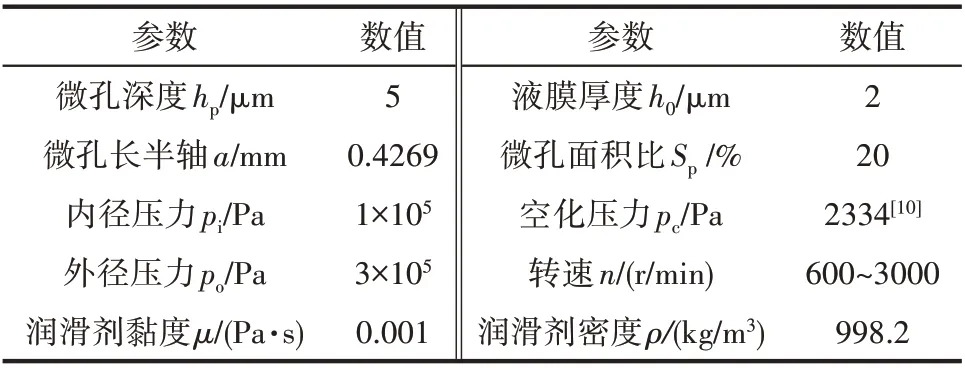
表1 计算参数Table 1 Calculation parameters

1.2 Fluent求解器设置

计算假设：（1）忽略温度、体积力和惯性力的影响；（2）密封间隙流体为牛顿流体，且黏度保持不变；（3）流体各相之间无相对滑动，流体与密封端面之间也无相对滑动；（4）流体流动为层流。

流动因子计算公式如下[28]

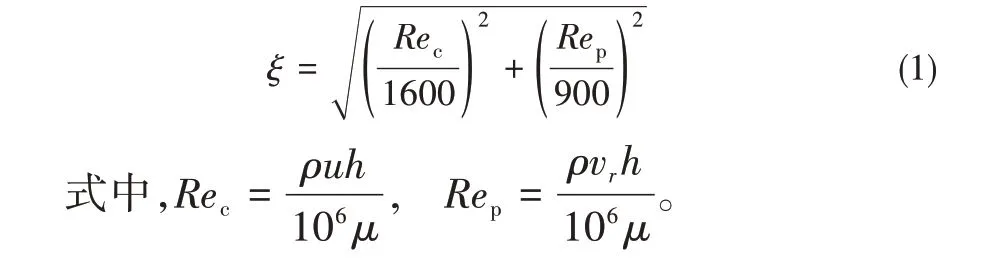
经过计算可知流动因子ξ＜1，流体流动状态为层流，故流动假设是正确的。

如图1（b）所示，周向两面设置为周期性边界；静环和动环表面均定义为壁面；外径处设置为压力进口，内径处设置为压力出口。

采用Mixture 多相流模型作为微孔端面密封间隙流体流动的计算模型，空化模型采用Zwart-Gerber-Belamri，因为其与实验结果最为接近[29]。压力与速度耦合算法采用SIMPLEC，动量离散方法采用Second order upwind，压力离散方法采用PRESTO，体积分数离散方法采用First order upwind。

密封间隙流体模型r-θ 平面尺寸为毫米级，z 向尺寸为微米级，有网格跨尺度无关性问题[30]。经过和文献[27]相同的网格无关性分析，网格全局尺寸取0.01 mm，微孔深度hp网格层数取8，液膜厚度h0网格层数取12。计算模型的正确性验证结果见文献[27]，计算结果与文献[31]的数据的平均相对误差为4.5%，平均绝对误差为0.0048 MPa。

1.3 泄漏性能的研究参数

泄漏率Q 是密封的主要性能参数之一，其计算公式如下

式中，dA 是泄漏截面微元面积，ρ 为流体密度，v为流体径向速度。

方向性微孔减少泄漏的主要原因有：（1）低压区对泄漏出口面（密封环内径）的流体的回吸[21-22]；（2）高压区对流体入口面（密封环外径）的流体的阻碍[8]。以上两点均使一部分流体往泄漏反方向流动，因此泄漏出口面和流体入口面的径向速度有正有负，正径向速度方向为泄漏反方向，负径向速度方向为泄漏方向。利用式（2）分别以正、负径向速度计算泄漏出口面和流体入口面的质量流量。泄漏出口面得到的质量流量为回吸率和外泄率，两者之和是泄漏出口面的净流率，即泄漏率。流体入口面得到的质量流量为回送率和流入率，两者之和为流体入口的净流率，其数值与泄漏率相等，符号相反。

基于以上分析，选择回吸率、回送率和泄漏率作为研究的参数。采用Fluent软件计算得到的回吸率为正值；回送率为负值；泄漏率为正值时表示负泄漏，泄漏率为负值时表示泄漏。

2 四种方向性微孔的多楔现象及对泄漏性能的影响

如图2 所示，在密封间隙端面法向（θ-z 平面）上，流体流进微孔，液膜厚度增大，形成发散性楔；流体流出微孔，液膜厚度减小，形成收敛性楔。如图3 所示，在端面切向（r-θ 平面）上，流体流经不同形状和方向角的微孔时，会产生不同的楔效应。整个密封间隙的楔效应受端面法向和切向两个平面的楔性结构的共同影响，本节将针对端面切向的楔效应进行研究。

在等边三角形的多楔现象[27]的研究中，为了建立方向角与多楔效应的联系，引入了“收敛角”，收敛角β 是楔与微孔中心的连线和线速度u 的夹角，其可以表征相同形状的微孔中楔的性质和强度。将收敛角β 的定义应用到椭圆形、菱形、矩形、等腰三角形微孔，各楔的收敛角β 如图3 所示。当β∈[0°,90°)，楔为收敛性楔，用▲表示，β 越小收敛性越强；当β=90°，楔为过渡性楔；当β∈(90°,180°]，楔为发散性楔，用▼表示，β越大发散性越强。

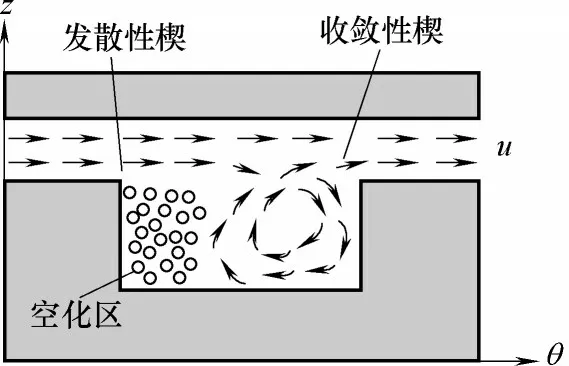
图2 端面法向的楔形结构Fig.2 Wedges structure of θ-z plane

2.1 四种方向性微孔的多楔现象

对于椭圆形微孔，如图3（a）所示，椭圆具有两个楔形结构A 和B，其形状结构完全一样，收敛角βA=α，βB=180°-α。由于βA和βB不同，所以两个楔产生的楔效应不一样。结合椭圆形微孔的压力分布，如图4 所示，与等边三角形微孔压力分布[27]不同，椭圆形微孔只有两个关于微孔中心点中心对称的楔形结构，其高低压区关于微孔中心近似中心对称分布，不存在明显的次级压力区域。由于本研究中涉及的中心对称均是关于微孔中心点的中心对称，所以后文将其简称为中心对称。

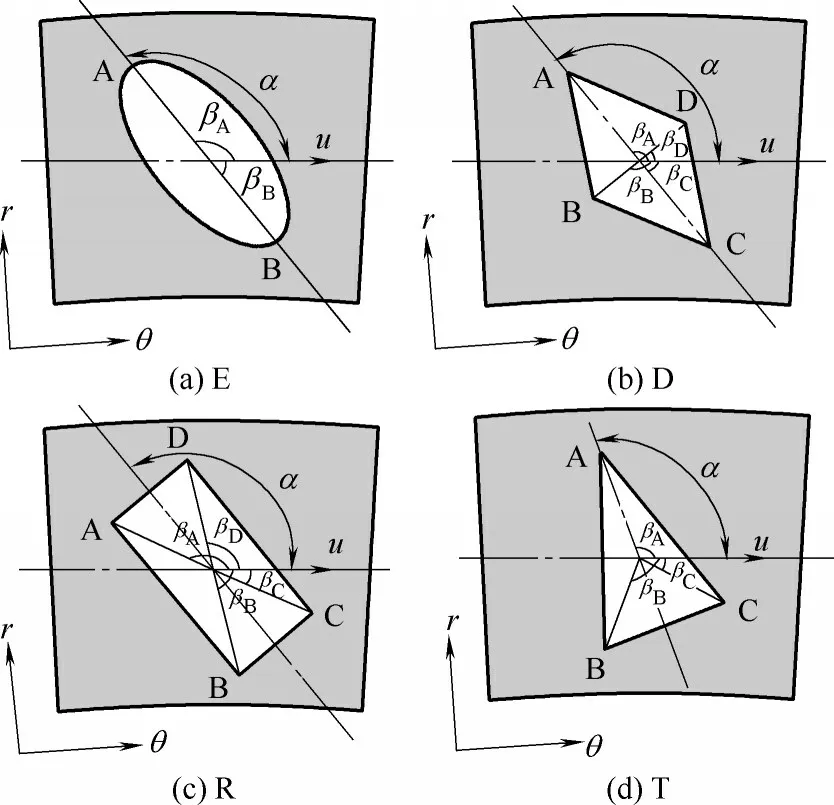
图3 四种方向性微孔的收敛角示意图Fig.3 Diagram of β of different dimples

对于菱形微孔，如图3（b）所示，其具有四个楔形结构A、B、C 和D，其中A、C 结构形状完全一样，B、D 结构形状完全一样，收敛角βA+βC=180°，βB+βD=180°。结合压力分布，如图5 所示，当α=0°，此时的楔形结构为（▲A▼C），B 和D 为过渡性楔；当α 由0°→90°时，A、D 两个楔组成一个大收敛性楔，B、C组成一个大发散性楔，即（▲AD▼BC）。大楔AD 和大楔BC 结构形状完全相同，可以当作两个中心对称的楔形结构，由压力分布图中高低压区近似中心对称分布也可以看出；在α=90°时，A、C 变成过渡性楔，楔形结构从（▲AD▼BC）变成（▲D▼B）；当α 由90°→180°时，楔形结构为（▲DC▼BA），与α∈（0,90°)一样，也可以当作两个中心对称的楔形结构；当α=180°，B 和D 变成过渡性楔，楔形结构为（▲C▼A）。由以上分析可知菱形微孔在任一方向角下都具有中心对称两楔结构。

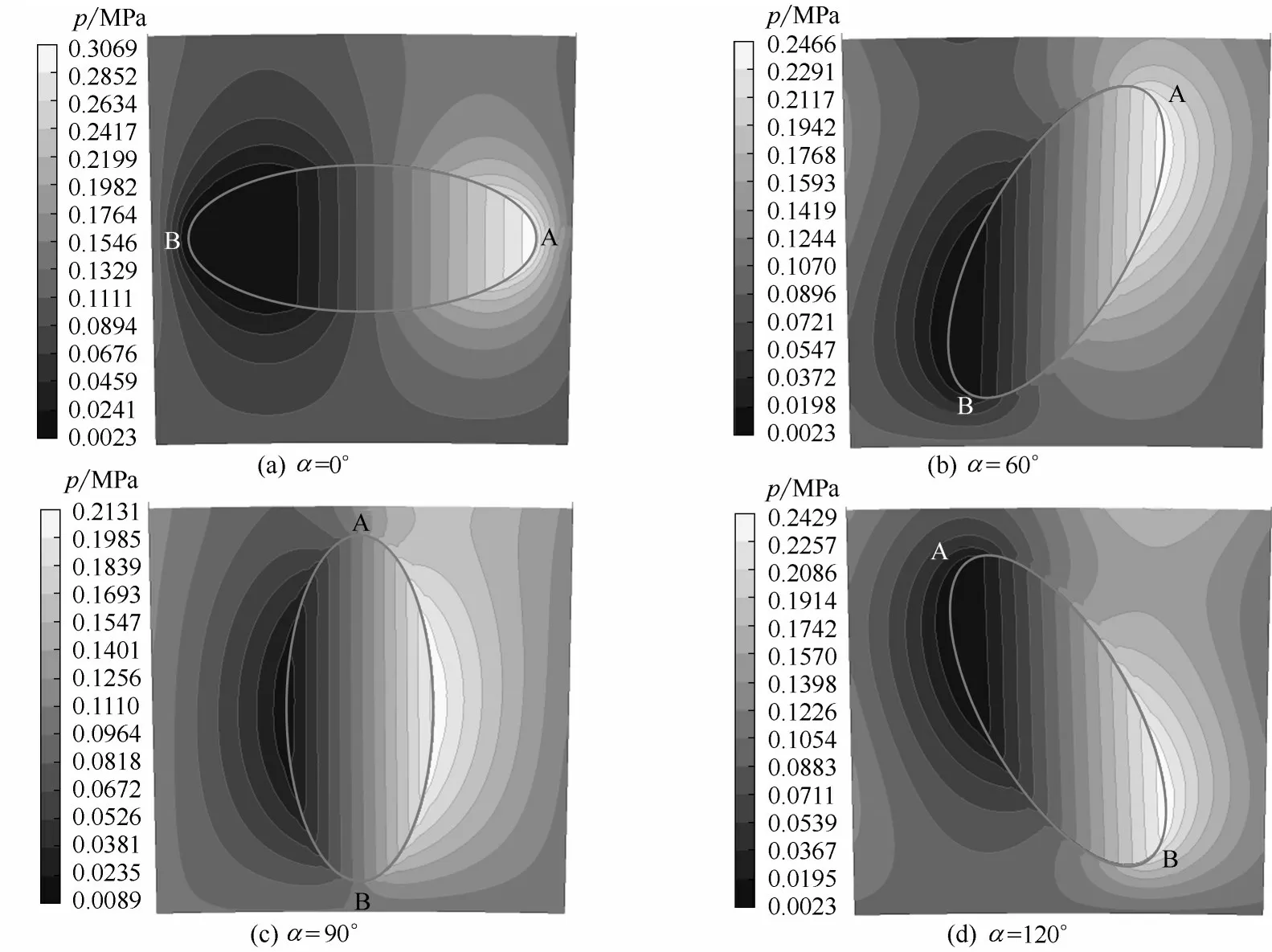
图4 靠近内径的微孔单元压力分布(E,n=2400 r/min)Fig.4 Pressure distribution of dimple unit close to ri(E,n=2400 r/min)

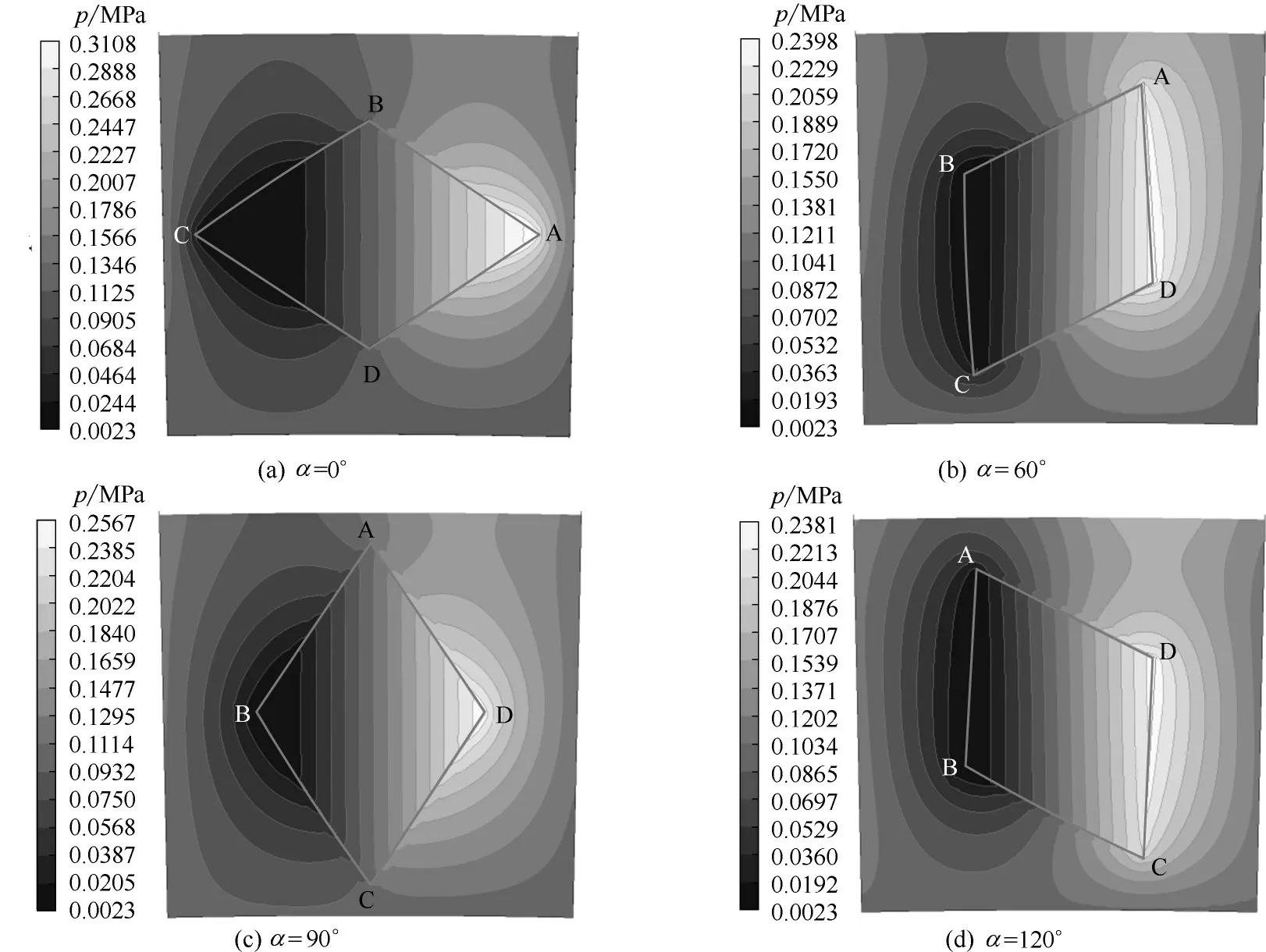
图5 靠近内径的微孔单元压力分布(D,n=2400 r/min)Fig.5 Pressure distribution of dimple unit close to ri(D,n=2400 r/min)

如图3（c）所示，与菱形微孔一样，矩形微孔也有四个楔形结构A、B、C 和D，并且形状结构完全一样，收敛角βA+βC=180°，βB+βD=180°。结合压力分布，如图6 所示，类比菱形微孔的分析，当α 由0°→90°时，楔形结构变化分为两段，先从（▲AD▼BC）逐渐变成（▲D▼B），再从（▲D▼B）逐渐变成（▲DC▼AB）；当α 由90°→180°时，楔形结构变化也分为两段，先从（▲DC▼AB）逐渐变成（▲C▼A），再从（▲C▼A）逐渐变成（▲BC▼AD）。结合压力分布图中高低压区近似中心对称也可以看出，矩形微孔在任一方向角下都具有中心对称的两楔结构。

对于等腰三角形微孔，如图3（d）所示，与等边三角形一样，也有三个楔形结构A、B 和C。不同的是，等边三角形的三个楔形结构形状完全相同，各楔之间的距离也相同，等腰三角形的三个楔形结构中B 和C 完全相同，而A 与B、C 不同。结合压力分布，如图7 所示，与等边三角形微孔[27]相比，等腰三角形微孔所产生的高低压区之间的距离较前者大，高低压区之间的相互影响较小，且等腰三角形底边处两楔形结构之间相隔很近，这两个楔的性质和强度很相近。

2.2 多楔现象对泄漏性能的影响

由于各转速下α 对密封泄漏性能的影响相似，限于篇幅原因，此节中仅展示了n=2400 r/min 时四种方向性微孔的回吸率Qs、回送率Qrf和泄漏率Q 随α 变化的曲线，如图8 所示。由于椭圆形、矩形、菱形微孔是中心对称形微孔，α 的变化周期为180°，所以分析Qs、Qrf和Q 在α∈[0,180°]内的变化即可，而等腰三角形不是中心对称形微孔，α 的变化周期是360°，所以需要分析Qs、Qrf和Q 在α∈[0,360°]内的变化。由图8 可知，椭圆形、菱形和矩形微孔的Qs、Qrf和Q 随着α 的变化规律是一致的，这是因为这三种孔型都具有中心对称性两楔结构，所以多楔现象对Qs、Qrf和Q 的影响规律是一致的。等腰三角形微孔的Qs、Qrf和Q 随α 的变化规律与前三种孔型稍有差异，这与等腰三角形楔形结构的非中心对称性有关。因此，选择椭圆形微孔和等腰三角形微孔的多楔现象对Qs、Qrf和Q的影响进行具体分析。

图6 靠近内径的微孔单元压力分布(R,n=2400 r/min)Fig.6 Pressure distribution of dimple unit close to ri(R,n=2400 r/min)

对于椭圆形微孔的回吸率Qs，由图8（a）和图4可知，当α 由0°→45°时，βA由0°→45°，βB由180°→135°，楔形结构为(▲A▼B)。▼B 的发散性减弱，由其产生的低压区压力逐渐减小，但由于低压区内压力保持为空化压力，故减小的幅度较小，同时低压区与泄漏出口之间的距离逐渐减小，两者综合，导致回吸率逐渐增大。空化与回吸率的影响关系，详见文献[21-22]。

当α由45°→135°时，βA由45°→135°，βB由135°→45°，楔形结构由(▲A▼B)→(▼A▲B)。由压力分布（图4）可以看出，此时低压区逐渐由▼B转换为▼A，导致低压区与泄漏出口之间的距离大幅增加，回吸压力梯度大幅减小，故回吸率大幅减小直至不再产生回吸现象，同时由于▼A 的发散性逐渐增强，由其形成的低压区压力逐渐降低，因此回吸率减小的趋势逐渐放缓。

当α 由135°→180°时，收敛角βA由135°→180°，收敛角βB由45°→0°，楔形结构为(▼A▲B)。此时▼A 所产生的低压区压力已经接近最低值，且低压区的位置与泄漏出口之间的距离也逐步减小，故此时回吸率小幅增大。

对于等腰三角形微孔的回吸率Qs，如图8（a）所示，在α∈[0°,180°]内，其回吸率随α 的变化趋势与中心对称两楔结构微孔基本一致，但回吸率的变化更加缓慢；在α∈[180°,360°]内，其变化趋势与中心对称两楔结构微孔完全一致。结合图7 来看，当α 由0°→180°时，发散性楔形结构由(▼B▼C)逐渐向▼A 转变。在这一区间内，(▼B▼C)是主要的发散性楔形结构。由于(▼B▼C)两楔形结构距离较近，故两者之间互相叠加，实质上增强了发散性楔形结构的强度，减缓了低压区压力升高的幅度，低压区的压力变化较为缓慢，因此回吸率的变化也较为缓慢。当α 由180°→360°时，发散性楔形结构由▼A 逐渐向(▼B▼C）转变。在这一区间内，▼A是主要的发散性楔形结构，此时等腰三角形微孔高压区与椭圆形微孔的情况相同，都只由一个楔形结构产生，因此其变化趋势与中心对称两楔结构微孔是一致的。

由以上分析可以知道，回吸率的主要控制因素为低压区，形成低压区的发散性楔形结构与泄漏出口之间形成的回吸负压压力梯度越大，则回吸率越大。

图7 靠近内径的微孔单元压力分布(T,n=2400 r/min)Fig.7 Pressure distribution of dimple unit close to ri(T,n=2400 r/min)

对于椭圆形微孔的回送率Qrf，需分析椭圆形微孔模型靠近外径的微孔单元的压力分布，由于各微孔单元压力分布规律相似，可以参考靠近内径处的微孔单元的压力分布，如图4 所示。结合图4 和图8（b），当α 由0°→45°时，βA由0°→45°，βB由180°→135°，楔形结构为(▲A▼B)，高压区与流体入口之间的距离逐步缩小，产生回送的正压压力梯度逐渐增大，回送率逐渐增大。同时由于▲A 的收敛性逐渐减弱，高压区压力逐渐降低，故回送率增大的趋势逐渐减缓。

当α由45°→135°时，βA由45°→135°，βB由135°→45°，楔形结构由(▲A▼B)→(▼A▲B)。收敛性楔形结构逐渐由▲A 转变为▲B，相较于前者，后者与流体入口之间的距离大幅增大，故回送率大幅减小。同时，当α 由90°→135°时，▲B 的收敛性逐渐增强，所以回送率减小的幅度逐渐减缓。

当α 由135°→180°时，收敛角βA由135°→180°，收敛角βB由45°→0°，楔形结构为(▼A▲B)。▲B 的收敛性逐渐增强，高压区压力逐渐升高，同时高压区与流体入口之间的距离逐渐缩小，在两者的共同作用下，回送率逐渐增大。

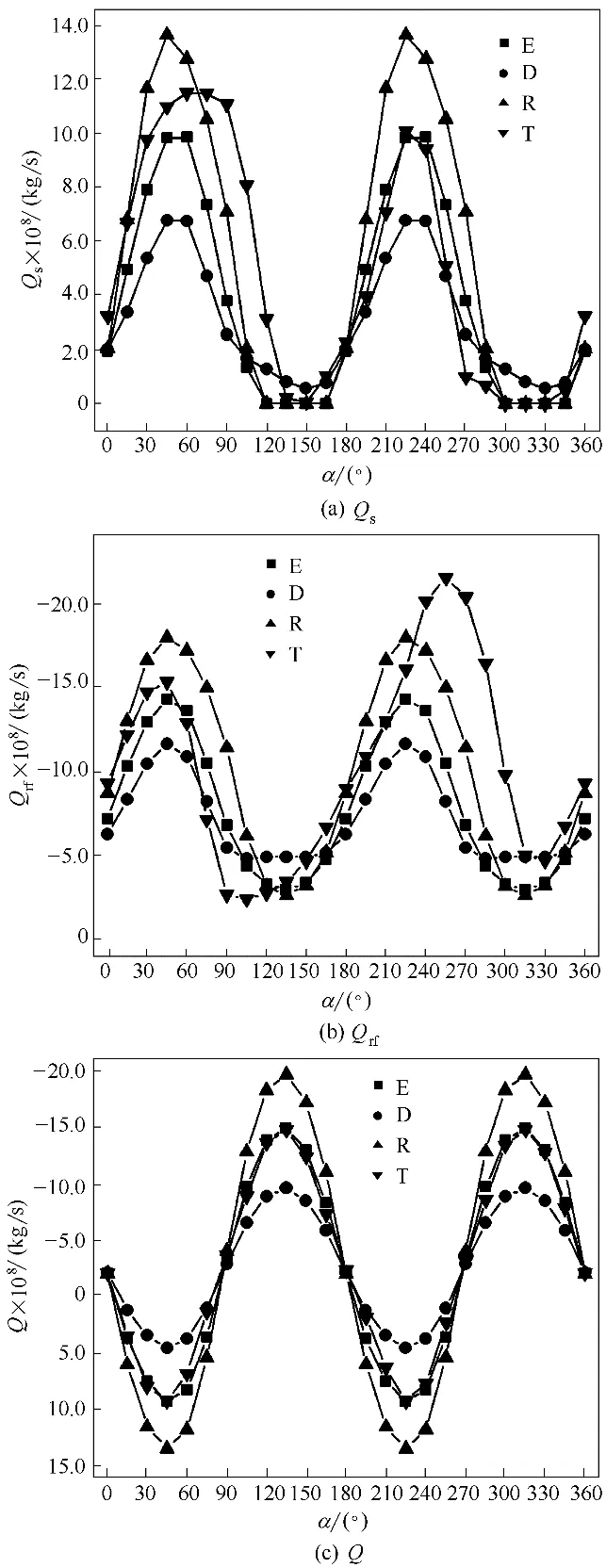
图8 α对Qs、Qrf和Q的影响(n=2400 r/min)Fig.8 Effect of α on Qs,Qrf and Q(n=2400 r/min)

对于等腰三角形，如图8（b）所示，在α∈[0°,180°]内，其回送率Qrf随α 的变化趋势与中心对称两楔结构微孔完全一致；在α∈[180°,360°]内，其变化趋势与中心对称两楔结构微孔基本一致，但回送率的变化更加缓慢。与椭圆形微孔一样，靠近外径处的微孔单元的压力分布规律可以参考靠近内径处的微孔单元的压力分布，如图7 所示。当α 由0°→180°时，收敛性楔形结构由▲A 逐渐向(▲B▲C)转变。在这一区间内，▲A是主要的收敛性楔形结构，此时等腰三角形微孔高压区与椭圆形微孔的情况相同，都只由一个楔形结构产生，因此其变化趋势与椭圆形微孔是一致的。在α∈[180°,360°]内，收敛性楔形结构由(▲B▲C)逐渐向▲A 转变。在这一区间内，(▲B▲C)成为了主要的收敛性楔形结构。由于(▲B▲C)两楔形结构距离较近，故两者之间互相叠加，实质上增强了收敛性楔形结构的强度，减缓了高压区压力降低的幅度，高压区的压力变化较为缓慢，因此回送率的变化也较为缓慢。

由以上分析可知，回送率的主要控制因素为高压区，形成高压区的收敛性楔形结构与流体入口之间形成的回送正压压力梯度越大，则回送率越大。

对于椭圆形微孔的泄漏率Q，如图8（c）所示，当α 由0°→45°时，βA由0°→45°，βB由180°→135°，楔形结构为(▲A▼B)。▲A收敛性减弱，但▲A形成的高压区与流体入口之间的距离逐渐减小，所以回送率增大。并且此时回吸率增大。两种因素都使泄漏率减小，故在该方向角区间内泄漏率减小。

当α由45°→135°时，βA由45°→135°，βB由135°→45°，楔形结构由(▲A▼B)→(▼A▲B)。此时回吸率大幅减小，并且相较于▲A 形成的高压区，由▲B 形成的高压区与流体入口之间的距离大幅增大，使回送率减小。两种因素都使泄漏率增大，故在该方向角区间内泄漏率大幅增大。

当α 由135°→180°时，βA由135°→180°，βB由45°→0°，楔形结构为(▼A▲B)。▲B 收敛性增强，高压区与流体入口之间距离减小，回送率增大。同时▼A 形成的低压区与泄漏出口间距离减小，所以回吸率增大，故泄漏率减小。

相比于前面的中心对称两楔结构微孔，等腰三角形微孔在α∈[0°,180°]内，回吸率随α 的变化更加缓慢，在α∈[180°,360°]内，回送率随α 的变化更加缓慢，但是趋势基本一致。如图8（c）所示，综合两者的影响后，其泄漏率的变化趋势在α∈[0°,180°]和α∈[180°,360°]内均与中心对称两楔结构微孔的变化趋势一致。

由以上分析可知，泄漏率受回吸率和回送率的综合影响，即受高低压区的综合影响。

3 基于楔结构组合的孔型设计

经过以上分析，得到了微孔形状对泄漏率的影响关系。具有较小泄漏率的微孔应该具有较强的回吸能力和回送能力，其几何特征应为：发散性楔形结构具有较强的发散性，使低压区与泄漏出口之间产生负压压力梯度，同时该楔形结构与泄漏出口之间的距离小；收敛性楔形结构具有较强的收敛性，使高压区与流体入口之间产生正压压力梯度，同时该楔形结构与流体入口之间的距离小。下面将根据上述几何特征，以菱形、椭圆形、矩形、等腰三角形四种方向性微孔为基础，通过楔形结构组合的方式，设计一个泄漏率更小的新孔型。

在设计过程中，保持长轴2a 和微孔面积比Sp不变，以保证新的微孔与四种方向性微孔的性能更具可比性，组合过程如图9所示，具体步骤如下。（1）选择两个楔形结构用来组合。以上四种孔型中，矩形微孔在α=45°时，其发散性楔形结构表现出最强的回吸能力，故选取该楔形结构进行组合，命名为▼R(α=45°)，如图9（a）所示。等腰三角形微孔在α=255°时，其收敛性楔形结构表现出最强的回送能力，故选取该楔形结构进行组合，命名为▲T(α=255°)，如图9（b）所示。（2）将两个楔形结构所属的微孔放置于同一平面上，并让▼R(α=45°)在泄漏出口侧，▲T(α=255°)在流体入口侧。（3）调整等腰三角形微孔的位置，使▼R(α=45°)的最远端与▲T(α=255°)的最远端的距离等于2a。（4）调整矩形微孔的短轴，使两个楔边界曲线围成的闭合图形的面积等于四种方向性微孔的面积。步骤（2）～步骤（4）如图9（c）所示。最终的几何形状如图9（d）所示，其中几何尺寸：c=0.4970，d=0.7900，e=0.2062。将组合设计成的新孔型命名为N 形孔，在图表中用N表示。

为了适应高压差或绝对不能泄漏的情况，所以期望泄漏率为正值，即发生负泄漏，并且该正值越大越好。由第2节可知，椭圆形、菱形、矩形、等腰三角形微孔在α=45°时的泄漏率与α=225°时的泄漏率相等，两个角度均为各方向性微孔泄漏率最小的角度，故仅将这四种方向性微孔在α=45°时的泄漏率与N 形孔的泄漏率进行对比，如图10 所示。可以看到，在实验工况下，五种孔型大部分实现了负泄漏，其中N 形孔的泄漏率最小，在n=3000 r/min 时，N 形孔的泄漏率相比于矩形、等腰三角形、椭圆和菱形改善了10%、50%、64%和222%。这是因为N 形孔由产生回吸率最大的发散性楔形结构与产生回送率最大的收敛性楔形结构组成，使影响泄漏的回吸能力和回送能力均得到了提升，故相比于其他四种方向性微孔，其泄漏率最小。

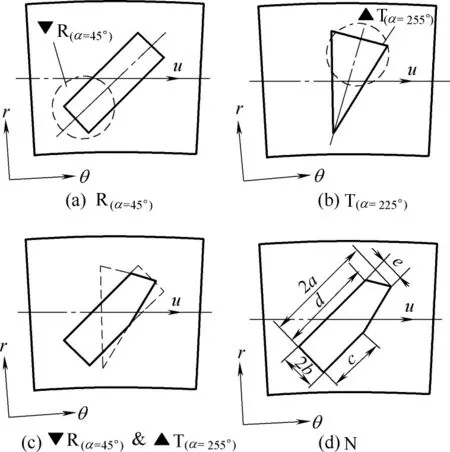
图9 N形孔的设计过程及几何模型Fig.9 Design process and geometric model of N dimple

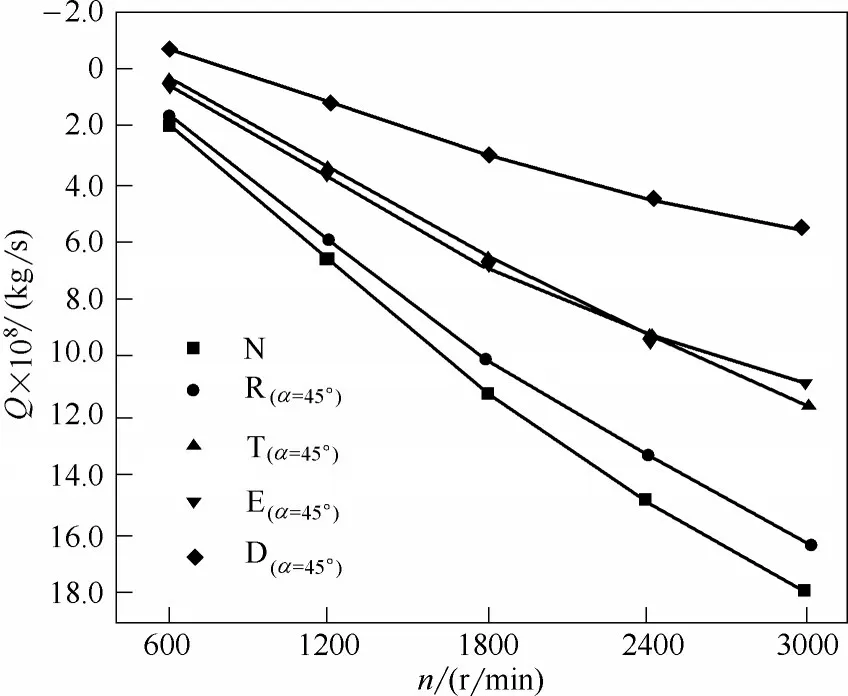
图10 E(α=45°)，D(α=45°)，R(α=45°)，T(α=45°)，N型微孔的泄漏率Fig.10 Leakage rate of E(α=45°)，D(α=45°)，R(α=45°)，T(α=45°)and N

4 结论

（1）应用等边三角形多楔现象的研究方法，对椭圆形、菱形、矩形和等腰三角形四种方向性微孔的多楔现象进行了分析。其中椭圆形、菱形和矩形微孔都表现为中心对称两楔性质的微孔，方向角对回吸率、回送率和泄漏率的影响规律都是一致的。等腰三角形微孔表现为非中心对称两楔性质的微孔，是介于中心对称两楔和三楔之间的孔型，虽然回吸率、回送率和泄漏率随方向角的变化与中心对称两楔性质的微孔稍有区别，但变化规律大致相同。

（2）影响微孔端面机械密封泄漏率的主要因素有回吸率和回送率。回吸率的主要控制因素为低压区，形成低压区的发散性楔形结构与泄漏出口之间形成的回吸负压压力梯度越大，则回吸率越大；回送率的主要控制因素为高压区，形成高压区的收敛性楔形结构与流体入口之间形成的回送正压压力梯度越强，则回送率越大。

（3）基于对多楔现象的理解，将四种方向性微孔中回吸能力最强与回送能力最强的楔形结构进行组合，设计出一种新的微孔，相比于原来的四种方向性微孔，其泄漏率最小。

符号说明

a——微孔长半轴，mm

b——微孔短半轴，mm

hp——微孔深度，μm

h0——液膜厚度，μm

pc——空化压力，Pa

pi——内径压力，Pa

po——外径压力，Pa

Re——Reynolds数

ri——密封环内半径，mm