三段管式非圆形域喷头驱动系统的结构设计及优化

齐 浩，朱华娟，弋景刚，任振辉，王泽河

(河北农业大学，河北 保定 071001)

0 引 言

喷灌技术是节水灌溉的主要手段之一[1]。为解决喷灌装备在工程应用中由于与目标地域的几何不相容性而产生的重喷、超喷等问题，国内外学者针对可自动调节射程和喷洒强度，实现非圆形域喷灌的喷灌装置开展了相关研究[2-8]，其中，实现喷头及射流阻挡装置运动的传动机构多采用仿形圆盘、齿轮、连杆装置等传统传动方案，从而容易造成重量、体积较大、传动精度不高、传动效率较低等常规问题。

精密钢丝绳传动以挠性传动为基本原理，通过钢丝绳与从动轮之间的静态摩擦力实现主、从动轮之间的力矩传递，该传动方式传动平稳、高效、维护简单、可适应不同复杂环境，美国公司最先提出了一种的精密钢丝绳传动机构，美国佛罗里达大学提出了一种双绕绳轮的精密钢丝绳传动机构，提出了一种正交精密钢丝绳传动机构，雅典国立科技大学机械工程学院也设计了一种钢丝绳系传动机构[9-12]。

本文通过研究三段管式非圆形域喷头的运动规律及运动学控制原理，将三段管式非圆形域喷头的喷射角度变化分解成控制旋转速率和仰角大小变化的旋转和偏转角度变化，研制了一套针对三段管式非圆形域喷头的“葫芦”型缠绕精密钢丝绳驱动系统，并期望通过拓扑优化、正交实验分析、参数优化的复合优化方法，提高三段管式非圆形域喷头驱动系统的综合性能。

1 三段管式非圆形域喷头的运动规律

如图1所示，三段管式非圆形域喷头的结构由三段管体和安装基座通过轴承依次连接构成，三段管体的端面均为圆形。由于三段管体的旋转轴线和喷头轴线之间存在夹角，通过喷头三段管体相对旋转使相邻两段喷头轴线夹角发生改变，实现喷射仰角的偏转。

喷头运动学控制规律为：

(1)

式中：Ω1、Ω2、Ω3分别为喷头三段管体的偏转角度大小；δN、δNy分别为喷头横、纵向偏转角度大小。

根据逆运动学规律，当喷头为最大喷射偏转角时：

Ω2=π,Ω3=-π

(2)

此时δN=4θ，本装置安装方案以竖直状态为0°偏转基准，至水平线的夹角为90°，因此选取θ=22.5°。

2 三段管式非圆形域喷头驱动系统的结构设计

2.1 三段管式非圆形域喷头旋转驱动系统设计

传动力矩作衡量传动能力的重要指标，其含义为：作为传动介质的钢丝绳在主动轮上全滑移临界条件下的负载力矩。在忽略钢丝绳的抗弯刚度、弹性伸长等因素的理想状态时，基于线性摩擦假设式的钢丝绳传动张力比满足[13]：

(3)

传动力矩为：

(4)

图2 三段管式非圆形域喷头旋转驱动系统原理图Fig.2 Schematic diagram of three-section tubular non-circular nozzle rotary drive system

由上式可知，传动包角θ越大，钢丝绳传动的传动能力越好，在传动包角θ，输入轮半径r1，摩擦系数确定的情况下，传动力矩仅与预紧力相关Tpreload。因此传统精密钢丝绳传动机构多采用“8”字缠绕，一方面可以实现使作用在轮轴上的径向力之间的互消，另一方面也可以增大传动包角，提高传动能力[14]。

但是由于“8”字缠绕方式钢丝绳交错部位会产生相互干涉，导致钢丝绳易产生错位和偏斜，当多组缠绕时，钢丝绳在主动及从动两轮上的缠绕过渡过程存在偏斜角,因此对钢丝绳导向槽的设计要求较高，根据“8”字形多组数缠绕角度及投影关系推得：随着螺旋槽的螺旋升角及传动比的增大，钢丝绳从螺旋槽中脱槽的概率也越大。

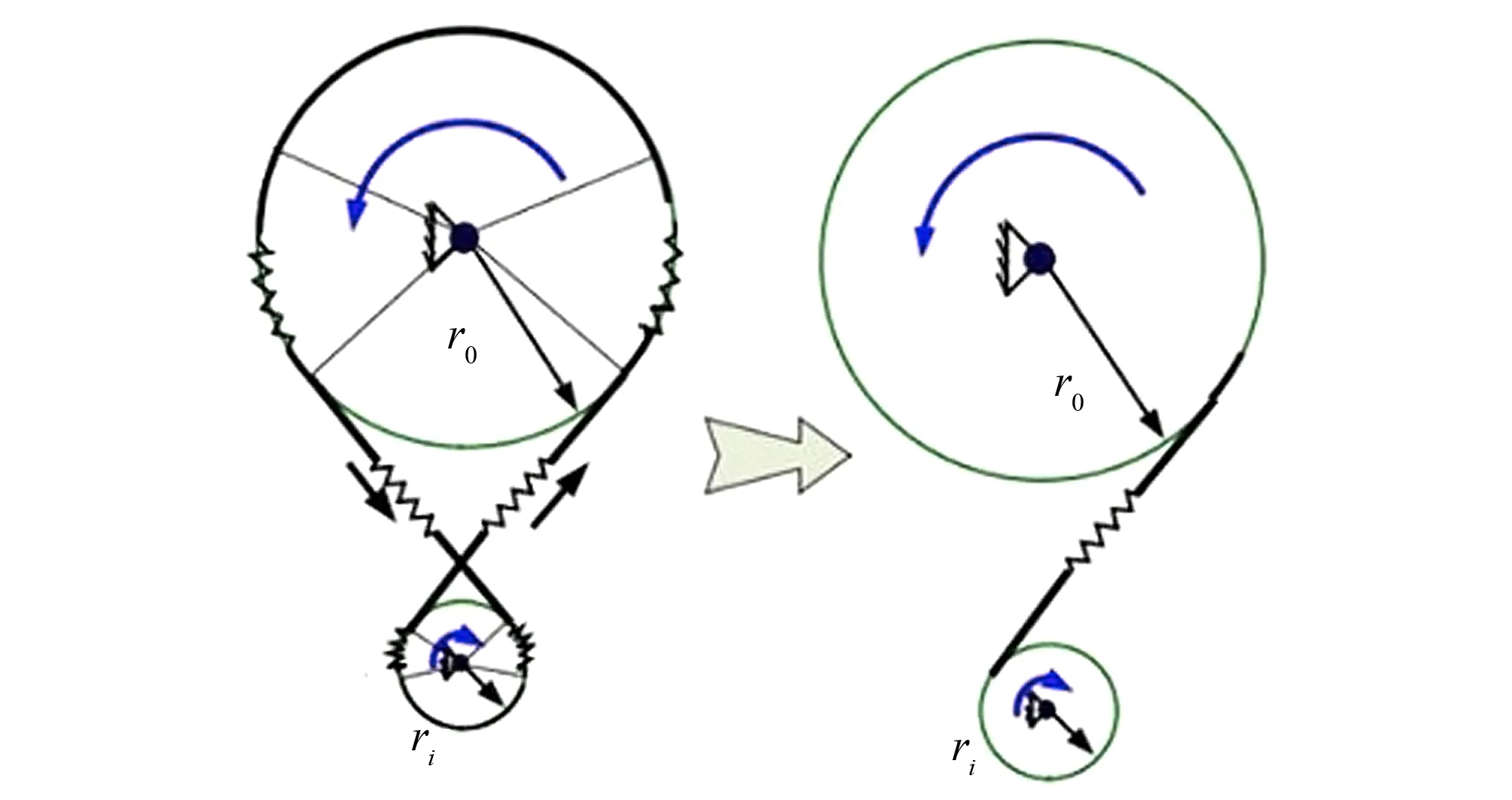
图3 钢丝绳“8” 字形缠绕方式等效模型Fig.3 Equivalent model of wire rope “8” word type winding method

本文根据“8”字形缠绕方式等效模型提出了如图4所示的一种“葫芦”型缠绕方式。“葫芦”型缠绕方式在传统开口式钢丝绳传动构型上，通过导向轮的限位作用，既保证了传动高负载要求中的大传动包角，同时提供了高效率的预紧力，又避免了钢丝绳缠绕时的干涉以及多圈缠绕时的绳槽偏斜角。

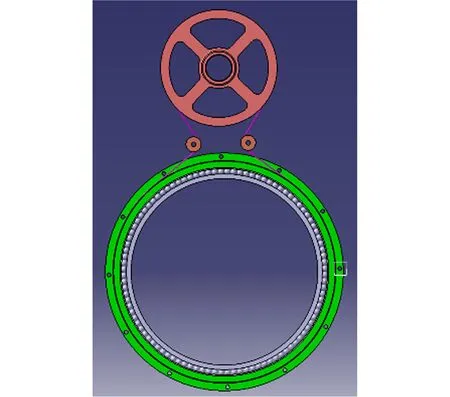
图4 “葫芦”型缠绕方式喷头旋转驱动系统示意图Fig.4 Schematic diagram of “Gourd type” winding mode nozzle rotation drive system

2.2 三段管式非圆形域喷头偏转驱动系统设计

三段管式非圆形域喷头的喷射角度通过3段管体的相对旋转实现偏转，由喷头运动学控制规律可知，喷头喷射角度变化时第一段管体与第三段管体的偏转速率相同，偏转角度相反，因此可通过一个驱动源驱动两段管体同步反向运动。

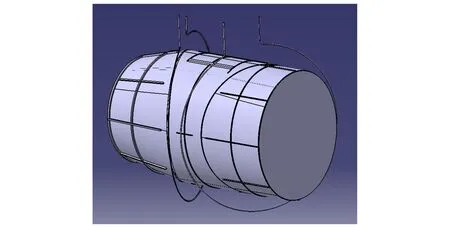
图5 “葫芦”型缠绕方式喷头偏转驱动系统原理图Fig.5 Schematic of “Gourd type” winding mode nozzle deflection drive system

本文所述三段管式非圆形域喷头偏转驱动系统包括3段喷头管体、1个驱动电机、1个钢丝绳换向机构、转向轮组和1根钢丝绳,钢丝绳通过依次绕过钢丝绳换向机构及转向轮组改变方向并对三段喷头管体进行“葫芦”型缠绕，通过驱动电机带动钢丝绳两端同步收放实现喷头三段管体之间大小相等、方向相反的相对转动。

图6 喷头偏转驱动系统原理图Fig.6 Sprinkler deflection drive system schematic

2.3 钢丝绳的设计与选择

钢丝绳在传动过程中，由于与传动轮啮合段入绳端与出绳端存在的拉力差，会产生相应的弹性滑移。同时由于钢丝绳与传动轮间静态摩擦力的存在，主动轮入绳端拉力由F0增大到F1，出绳端拉力F0则由降到F2。设拉力变化量为ΔF[15]，则：

(5)

设Mc为从动轮输出力矩，力矩平衡关系为：

(6)

可按下式来确定预紧力F0。

(7)

式中：Mf为负载力矩，N·m；μs为绳、轮当量摩擦系数；θ1为绳与主动轮传动包角，rad；K为钢丝绳组数；D2为从动轮直径，mm。

式中：S为最大静拉力(S=F1)，N；C为选择系数。

综上所述，本文选择直径0.8 mm的同向捻制钢丝绳。

3 三段管式非圆形域喷头驱动系统的性能测试

由于外力主要经钢丝绳通过导向轮作用于三段管式非圆形域喷头旋转驱动系统安装支架上，故着重对安装支架进行性能分析。利用Ansys-Workbench软件进行静力分析，采用四面体-六面体混合网格的方法进行划分，模型中共包含有162 761个节点，96 925个单元。模型材料均采用2A12T4。

图7 静应力Fig.7 Static stress

图8 静变形Fig.8 Static deformation

计算得出安装支架的质量为422 g，安装支架的静应力和静变形如图7和图8所示。可知其最大静应力为76.065 MPa，最大静变形为0.023 mm。

机械结构通常是低阶振动最先产生，低阶振动也是结构的主要振动形式，所以分析前两阶固有频率和振型。

根据图9，可知安装支架的第一阶固有频率为383.25 Hz，安装支架沿着Y轴方向振动；模型的第二阶固有频率为1 059 Hz，模型沿着X轴方向振动。

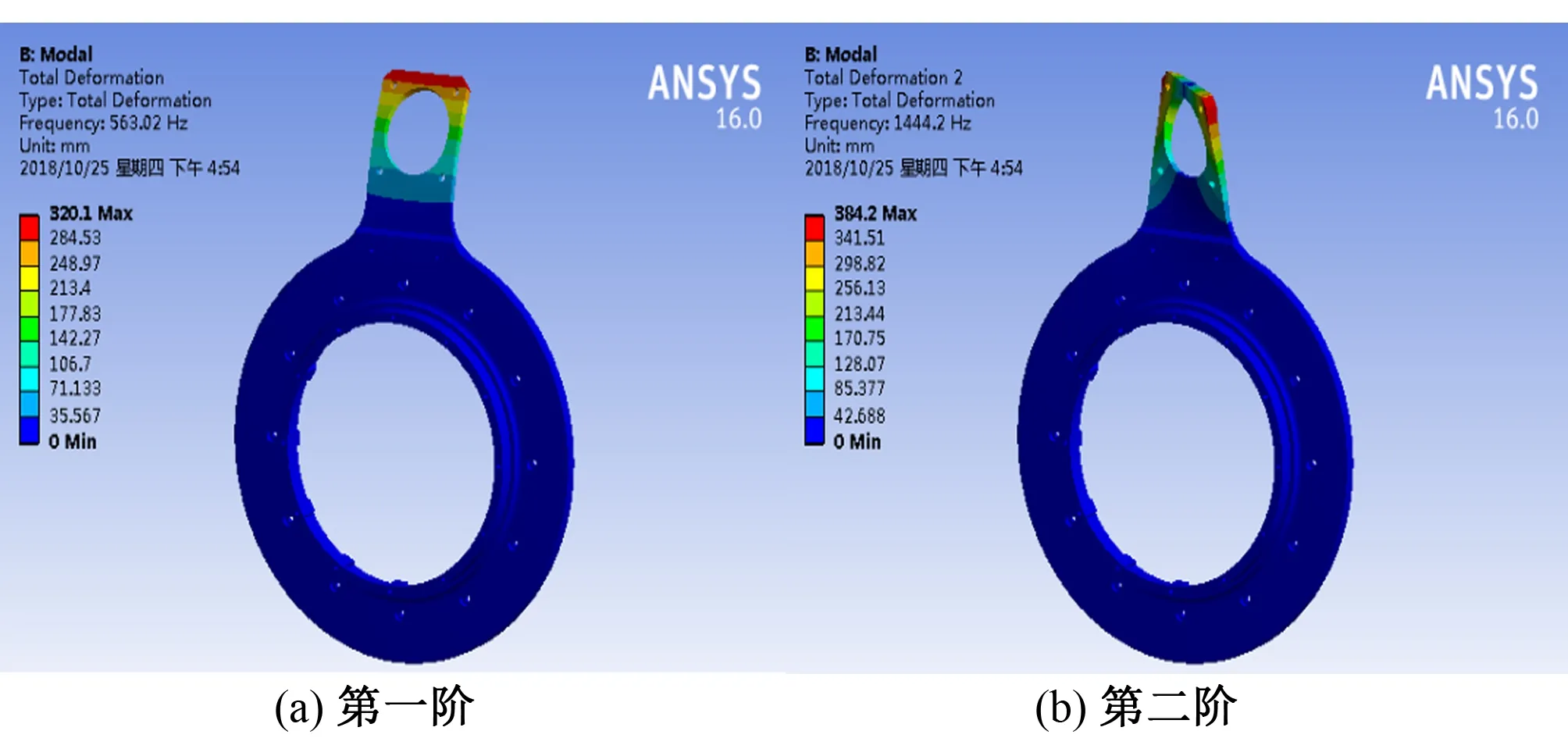
图9 振型云图Fig.9 Vibration pattern

根据模态分析的结果可知安装支架的主要振型为X和Y轴方向振动。安装支架的振动特性直接影响钢丝绳与主、从动轮之间的相对位置，进而影响喷头的旋转精度，因此谐响应分析时以舵机转子插口平面中心节点的频响特性为研究对象。分析结果如图10所示，模型轴Y最大振幅0.048 19 mm，Y轴最大振幅0.014 493 mm。

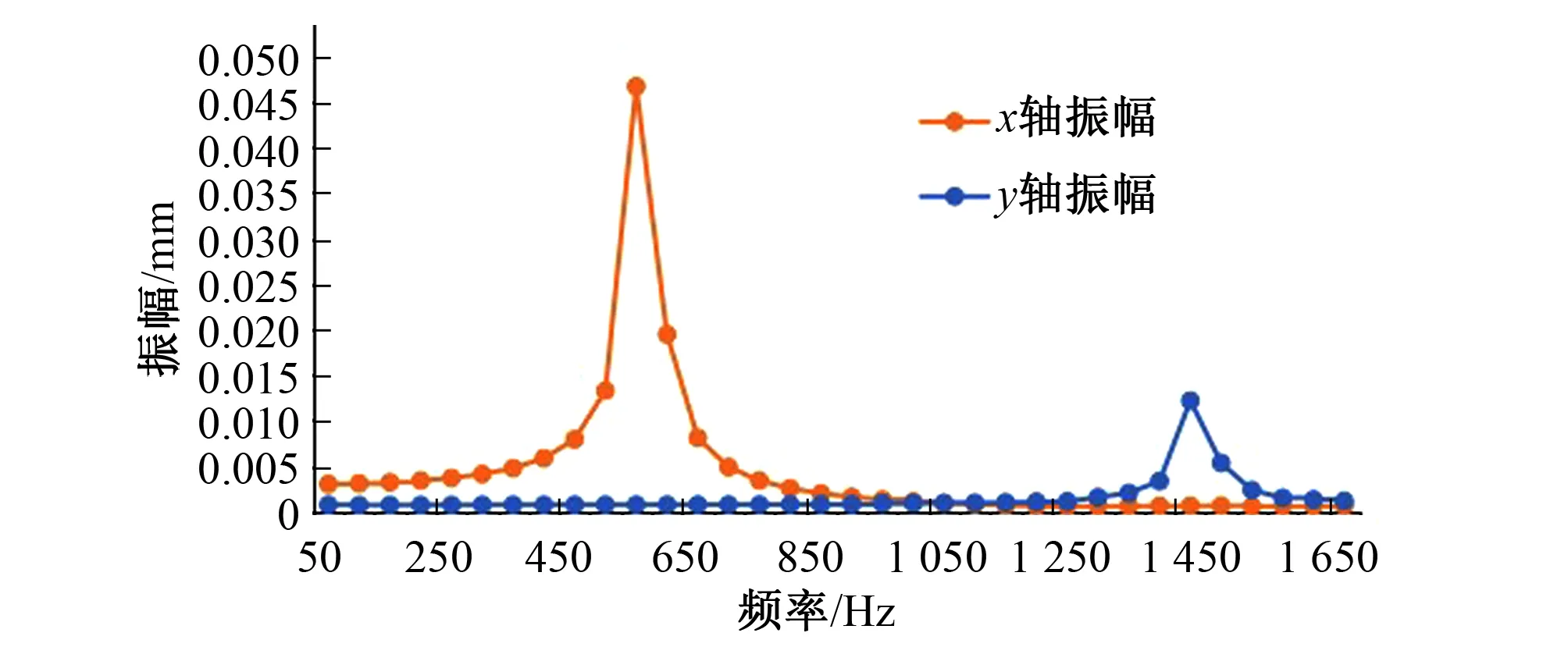
图10 安装支架频响曲线Fig.10 Mounting bracket frequency response curve

同理，针对三段管式非圆形域喷头偏转驱动系统的主要承载部件安装支架采用相同方法进行性能分析，计算得到三段管式非圆形域喷头偏转驱动系统的安装支架的质量为282 g，最大静应力为117.75 MPa，最大静变形为0.056 mm，第一阶固有频率为487.63 Hz，安装支架沿着Y轴方向振动；模型的第二阶固有频率为1 249.77 Hz，模型沿着X轴方向振动，Y轴最大振幅0.064 894 mm，X轴最大振幅0.025 764 mm。

精密钢丝绳传动中的精度主要衡量指标为主、从动轮之间的扭转角度偏差α[16]，可用下式求解：

(8)

根据驱动系统负载与精度试验，得到传动精度与负载关系如图12所示。

图11 驱动系统负载力测试试验装置Fig.11 Drive system load force test experimental device

图12 传动精度与负载关系Fig 12 Transmission accuracy and load relationship

4 三段管式喷头驱动系统的结构优化

为最大限度提高三段管式非圆形域喷头驱动系统的动态性能，对上述原型安装支架进行多目标拓扑优化设计。为了得到最优的拓扑结果，需要将拓扑优化初始模型的内部填实。

通常结构在共振点的振幅与结构固有频率呈反比，因此拓扑优化时以原型安装支架的前两阶固有频率最高为拓扑优化目标，同时为使优化结果具有轻质性且满足工程属性要求，优化时以安装支架的质量最小、静变形和静应力不超过原型结构、静应力和静应变均不大于2A12T4材料的屈服应力和应变为拓扑优化目标。

本文采用Shape Optimization(Beta)模块结合变密度法对三段管式非圆形域喷头旋转驱动系统安装支架进行拓扑优化设计，得到的拓扑优化结果如图13所示。

图13 拓扑优化结果Fig.13 Topology optimization result

根据图13可知，优化后的模型中存在许多不规则的边缘，使其加工困难，结合现有制造工艺和2A12T4材料的加工特性对拓扑优化结果进行结构重构，使其便于加工制造，如图14所示。

图14 重构安装支架模型Fig.14 Reconstructed mounting bracket model

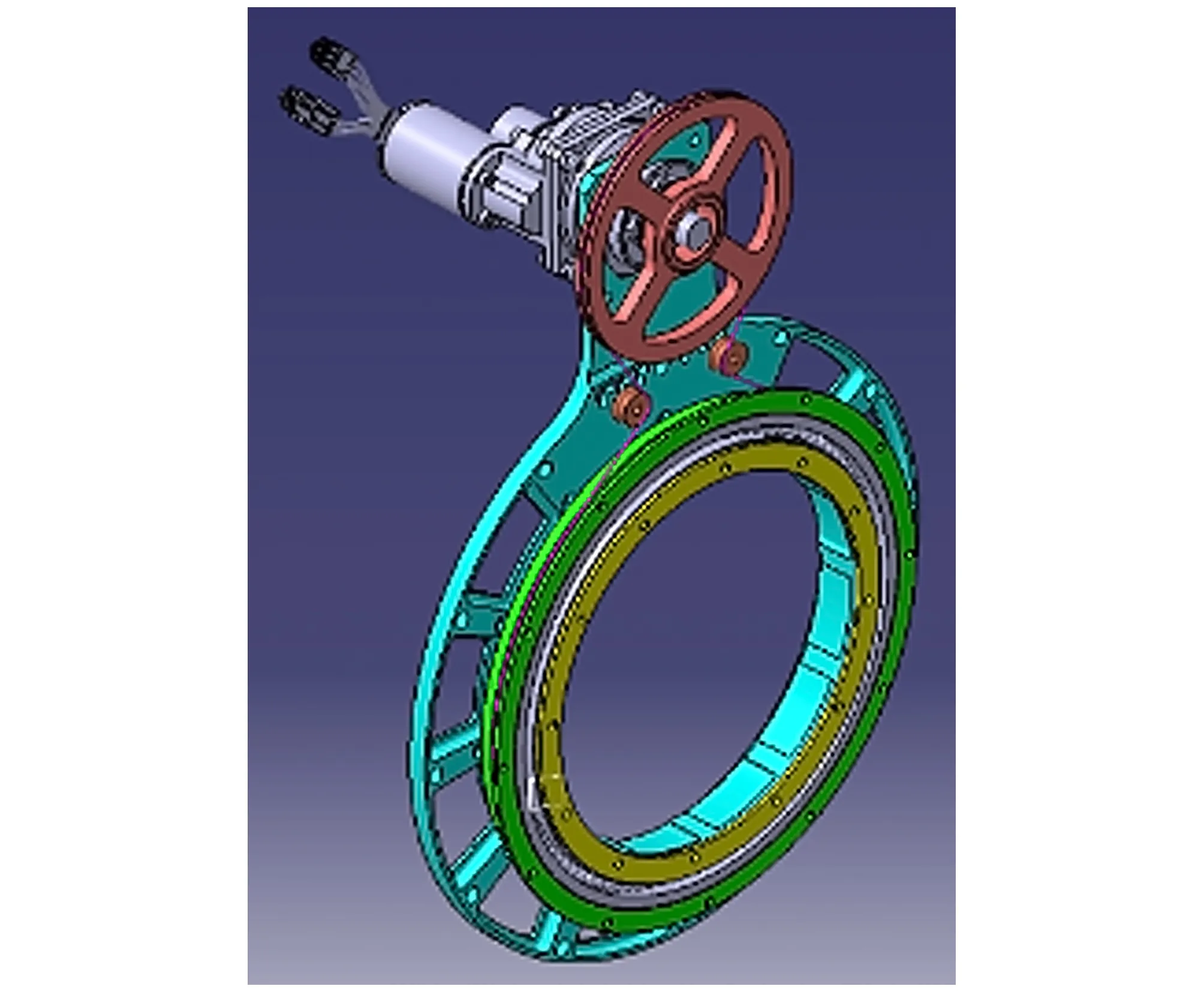
图15 优化后的喷头旋转驱动系统Fig.15 Optimized nozzle rotary drive system

采用同样的方法对三段管式非圆形域喷头偏转驱动系统安装进行优化，由于传动过程中钢丝绳不仅沿绳轮径向进行缠绕运动，同时，钢丝绳沿绳轮轴向方向也发生位移。若钢丝绳在主、从动轮上的轴向位移不同步，不等大，钢丝绳将发生脱槽，最终导致卡死现象。

传统钢丝绳传动系统为避免卡死现象，需对主、从动轮增加主、从动轮螺距比等于传动比、两轮绳槽的螺旋升角等大等设计限制条件，以保证钢丝绳传动系统在传动过程中主、从动轮产生同等大小的轴向位移。

本文所研制的三段管式非圆形域喷头偏转驱动系统中，通过钢丝绳换向机构上的螺纹运动补偿装置在喷头偏转过程中通过抵消钢丝绳在偏转过程中产生的轴向位移，既保证了大传动比，又减免了复杂的钢丝绳槽设计，同时对钢丝绳传动系统轴向位移的运动补偿，保证了钢丝绳缠绕过程中的扭转角度偏差。

优化后结果如图16所示。

图16 重构安装支架模型Fig.16 Reconstructed mounting bracket model

图17 优化后的喷头偏转驱动系统Fig.17 Optimized nozzle deflection drive system

因为拓扑优化结果只是对结构布局的优化，而上述优化结果都掺杂了经验设计方法，并未达到最优尺寸，所以重构模型时还应重点关注各重构结构尺寸参数。针对三段式非圆形域喷头偏转驱动系统安装支架初选20个结构尺寸作为研究因素，如图18所示。每个因素取3个水平，通过正交实验方法判定各因素对安装支架的前两阶频率和X、Y、Z轴方向振幅及质量的影响因数。

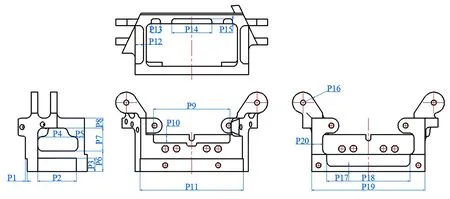
图18 设计因素Fig.18 Design factor

正交实验中极差的大小表明因素对研究目标的影响，由图19可知，影响第一阶频率最高的两个因素为P5和P20；影响第二阶频率最高的两个因素为P11和P16；影响质量最大的两个因素为P11和P20。

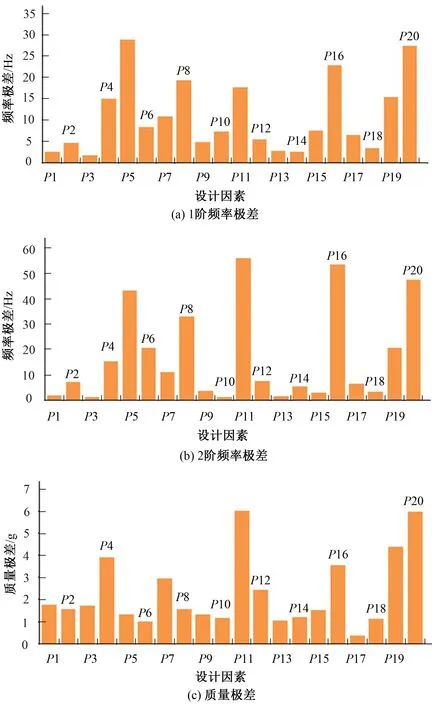
图19 极差分析Fig.19 Range analysis

综上分析可知影响安装支架性能的关键因素为P5、P11、P16、P20，将其作为参数优化的设计变量。根据正交实验各因素中水平计算结果确定非关键因素大小。

在CATIA软件中对零部件标注时加入DS_，使得Ansys-Workbench软件的parameters可编辑，利用Design Modeler模块建立安装支架的参数化模型，并通过Response Surface模块研究各设计变量对重构模型性能的响应。

在响应曲面分析结果上，对各设计变量进行多目标参数优化设计。优化时以P5、P11、P16、P20为设计变量，其范围与正交实验时各因素的水平范围相同；以重构模型的静变形和静应力不大于原型结构的30%为约束条件，以重构模型的最大应力和应变不大于2A12T4材料的屈服应力和应变为约束条件；以重构模型沿3个轴向振幅及模型质量分别最小为目标函数，该优化问题的数学模型为:

minF(ρ)=[f1(P),f2(p),f3(P),f4(p)]T

(9)

式中：f1(P)、f2(p)、f3(P)、f4(p)分别为安装支架谐响应振幅和质量；σ′(ρ)、σ′(ρ)、D′(ρ)、ε′(ρ)分别为安装支架的静应力、静变形、静屈服应力及静应变。采用screening法进行优化，设置样本点数为100。

根据优化后的参数大小建立安装支架模型，计算得出优化后的安装支架质量为79 g与原型282 g相比减轻了72%，对优化后的安装支架进行静力学分析，最大应力为109.73 MPa，最大静变形为0.057 mm。分别比原型安装支架减小9.32%和增加1.79%；前两阶固有频率分别为521.76 Hz和1 307.19 Hz，相比原型提高了7%和4.59%；对优化后的安装支架进行相同节点位置、激振力大小的相同约束条件下的谐响应分析，得到，Y轴最大振幅0.048 67 mm，比原型减小了25.1%；X轴的最大振幅0.016 056 mm，比原型减小了34.1%。同理，对三段式非圆形域喷头旋转驱动系统安装支架进行相同方法优化。

5 结 论

本文针对一种新型三段管式非圆形域喷头，研制了控制喷头非圆形域喷灌、实现自动调节射程和喷洒强度的喷头驱动系统，并根据其运动规律及控制原理将控制驱动系统分为旋转驱动及偏转驱动两套子系统以分别实现旋转速率和仰角大小变化，得到如下结论。

(1)新型三段管式非圆形域喷头驱动系统采用精密钢丝绳传动方式，效率高、无需润滑、环境适应性强，维护方便、在保证高精度传动的同时较传统传动方式结构更为简单、紧凑且极大地降低了系统重量，为喷灌装备的驱动系统设计应用提供了新的思路和方法。

(2)通过“8”字形缠绕等效模型提出的“葫芦”型缠绕方式，可以在保证高负载传动大传动包角要求的同时，避免钢丝绳缠绕时的干涉以及多圈缠绕时的绳槽偏斜角等诸多问题，同时合理的结构设计可以在进行钢丝绳缠绕限位的同时提供高效率的预紧力。

(3)针对三段管式非圆形域喷头驱动系统，通过高集成的结构设计减少了一个驱动源的需求，降低了经济成本、安装空间及复杂程度，并采用拓扑优化设计、正交实验、参数优化设计相结合的方法设计并得到了最优参数，结果表明，优化后的喷头驱动系统部件在满足强度、刚度等前提下质量得到大幅减轻，且静、动态等性能均有不同程度的提高。