带经济器补气的单螺杆压缩机空气源热泵系统模拟分析

刘闪威，鹿院卫，吴玉庭, 雷 标, 温强宇，智瑞平, 马重芳

(1.北京工业大学环境与能源工程学院，北京 100124；2.传热强化与过程节能教育部重点实验室，北京 100124)

热泵(heat pump)是一种消耗一定的机械能，将低温位热能送到高温位来供应热量需求的设备[1]. 空气源热泵是消耗一部分电能，从环境中获取低品位热能，具有高效节能、绿色环保、使用便利、操作简单等优点，因此空气源热泵应用极其普遍，是实现国家节能减排目标，改善环境污染的重要技术途径之一. 在环境温度相对较高时，空气源热泵能得到良好的运行效果，而在室外环境温度较低时，存在压缩机压比大、压缩机排气温度过高、其制热量和能效比衰减严重等问题，制约着空气源热泵在寒冷地区的大规模应用[2]. 为解决该问题，目前应用了多种措施，如复叠式循环系统、双级压缩循环系统、控制除霜、新型工质替代和经济器补气等措施，其中具有压缩机经济器补气技术的空气源热泵系统是空气源热泵性能能够得到提高的一个较好的解决方案[3].

补气型压缩机是热泵机组经济器补气系统的关键设备之一. 近年来，国内外众多学者针对补气型压缩机开展了大量的理论与试验研究，并取得了阶段性成果. 其中，林镝等[4]把补气型活塞压缩机应用于冰箱，获得了2种蒸发温度，分析并得到了良好的效果. Yan等[5]研发了一款空气源热泵用补气型双转子压缩机，补气口开设在气缸上，气缸内转子可周期性覆盖补气孔口，补气口也因此定期开启、封闭，从而实现压缩过程中补气. 补气以后，制热量提高5.6%～14.4%，系统能效比(coefficient of performance，COP)最大提升3.5%. Wang等[6]和Liu等[7]把补气口设在滑片上，并采用补气单向阀来避免补气回流. 试验结果表明：制热量和COP分别增加12.9%～15.7%和1.5%～4.1%. 胡文举等[8]在涡旋压缩机的基础上，分析了补气压力损失系数与一级压比对补气增焓空气源热泵系统性能的影响. Dardenne等[9]和Cho等[10]建立基于涡旋压缩机补气过程模型，并对补气回流的特性进行了分析. 在试验层面，戴源德等[11]、Wang等[12]、Navarro等[13]、张剑飞等[14]和高飞等[15]通过补气均使制热量和COP得到一定提升. 值得一提的是Qin等[16]加设了补气单向阀，在-20℃环境温度下通过补气使制热量提升了31%.

目前关于补气型涡旋压缩机的研究取得了显著的成果，并且产品在小型空气源热泵应用方面也取得了显著的效果. 然而在大中型空气源热泵应用方面，多采用模块机组，增加了系统的复杂程度. 吴华根等[17-18]通过在阴转子中埋入传感器，实际测量了补气型双螺杆压缩机的p-V图. 近年来，孙超等[19]、杨丽等[20]和赵华[21]对双螺杆压缩机补气过程进行了研究，得到的基本结论为：如果以最大制热量为目标，则补气应在进气封闭以后立即开始，如果以最大COP为目标，则补气压力存在某个最佳值. 和双螺杆压缩机一样，单螺杆压缩机也具有单向吸气、单向排气特性，可以方便地进行补气. 公开文献[22-25]中有研究者对单螺杆压缩机的磨损、泄漏、型线和传热等问题进行了细致的研究，但关于补气的研究公开文献较少. 李闯等[26]对闪发器热泵单螺杆压缩机的补气位置进行了模拟，计算表明单螺杆压缩机的补气位置应在压缩机螺槽刚封闭时开设补气孔，但并未进行试验验证.

综合以上文献，其中理论分析大都建立在2个基本假设上. 一是认为补气过程进行得异常迅速，因而将补气过程视为容积不变的绝热等容过程,但实际上，补气是一个相对较长的过程，在补气的过程中，基元容积有较大的变化，因此补气过程被假定为等容过程，得到的计算结果显然会带来较大的偏差. 二是一部分文献将理想气体状态方程引入到中间补气过程的能量方程中，实际气体状态参数与理想气体状态参数也相差较大，尤其是对制冷剂而言，因此用理想气体状态参数计算得到的补气分析结果，并不能很好地指导实际.

本文以补气型单螺杆压缩机几何关系为基础，以非稳定流动开口系能量方程、质量守恒方程以及实际气体状态方程等为基本方程，尝试建立更接近于实际补气状态的数学计算模型，利用四阶龙格- 库塔法对该数学模型进行分析求解，以求得到空气源热泵系统机组性能以及补气型单螺杆压缩机工作腔内部的相关热力参数，并与常规单级热泵系统进行对比分析.

1 单螺杆压缩机经济器补气系统

经济器补气循环系统中，经济器形式主要分为闪发式和换热器式，本文以闪发式经济器形式为基础对循环系统进行分析. 经济器循环系统原理如图1所示，压缩机采用的是单螺杆压缩机. 图中，1为压缩机进气状态，2为一级内压缩终了后的状态，3为压缩机排气状态，4为蒸发器出口的工质状态，4′为膨胀阀a出口状态，5为经济器内饱和液状态，m为经济器内饱和气状态，5′为膨胀阀b出口状态。pk、pm和po分别表示压缩机的排气压力、补气压力和进气压力. 图1中冷凝器出来的制冷剂液体经过膨胀阀a的一次节流，进入经济器，此时经济器内的制冷剂为饱和态，闪发出的饱和制冷剂蒸气进入单螺杆压缩机补气口，液体制冷剂则经主回路的膨胀阀b进入蒸发器，制冷剂从蒸发器吸收热量变成相应的低压气体，进入单螺杆压缩机，在单螺杆压缩机内部，吸入的制冷剂气体经过一定的压缩后和补气管路中的气体混合，经过边压缩边混合的过程之后，一起被压缩至排气压力，再进入冷凝器冷凝成液体，完成整个循环.

2 热力学工作模型的建立

带补气的单螺杆压缩机的工作过程可分为4个阶段：

1) 一级内压缩过程. 这一过程，补气没有介入，压缩腔内的工质被压缩是由于受螺杆和星轮的旋转啮合作用，其状态是从蒸发器吸入的过热蒸汽压缩到补气口打开前的状态.

2) 经济器补气过程. 从经济器出来的制冷剂气体经过补气管路，从补气孔口补入压缩腔内，与原有的制冷剂气体混合，随着星轮与螺杆的啮合转动，进行边补气边混合压缩，直至压缩腔与补气口分离.

3) 准二级压缩过程. 压缩腔与补气口分离后，混合后的制冷剂随基元容积的减小而继续被压缩，直到压缩腔与排气口连通.

4) 排气过程. 当压缩腔与排气口连通之后，压缩机开始排气，由于实际运行中，压缩机总会出现过压缩或欠压缩，因此排气过程大多会是一个等容压缩或膨胀过程，排出的气体进入冷凝器冷凝.

为了建立更接近于实际的数学模型，本文分两部分进行模型的建立与分析，着重建立经济器补气过程的数学模型并进行分析.

2.1 带补气的基元容积内压缩过程模型的建立与分析

本文以单螺杆压缩机的一个螺槽为基准，将压缩腔内进行的补气- 压缩过程抽象为如图2所示的非稳定流动的热力过程. 假定在单位时间dτ内，通过轴传动给螺杆的功为dW，进而使得螺杆工作腔内的介质被压缩，由螺杆旋转引起的压缩腔容积的变化为dV，经补气口进入压缩腔的制冷剂参数分别为质量dms、焓hs、温度Ts，由相邻高压腔内泄漏流入控制容积内部的制冷剂参数分别为质量dmi、焓hi、温度Ti，由控制容积内泄漏流向低压腔的制冷剂参数分别为质量dmo、焓ho、温度To. 控制容积内的质量增量为dmsys.

为了将复杂的过程更好地用数学模型表述，对压缩过程提出以下假设:

1) 压缩机吸入的制冷剂全部为制冷剂气体.

2) 忽略流动过程中的动能、势能以及流动损失的变化，并假定任意时刻，基元容积在相同的转子转角位置时，其内的工质状态参数相同.

3) 将基元容积中的制冷剂气体和润滑油分别视为2个相互独立的系统，系统间没有能量交换.

4) 吸排气腔中无压力脉动，气相和液相的压力始终相等，吸排气压力等于名义吸排气压力.

5) 介质通过泄漏通道的流动均为绝热流动，且服从无摩擦喷管流动规律.

6) 中间补气过程，进入的基元容积的制冷剂为不含润滑油的纯气体.

对控制容积应用质量守恒定律有

dmsys=dms+dmi-dmo

(1)

在模型假设条件下，由于控制容积压缩过程中气体流出的速度较小，因此忽略了动能、势能的变化，由能量守恒定律可得

d(mu)=∑dmihi-∑dmoho-dQ+dW

(2)

式中：m为控制容积内工质的质量；u为控制容积内工质的内能；Q为控制容积与外界所交换的热量.

由气体热力学状态方程关系式可得到与螺杆转角的变化关系：

(3)

(4)

经过以上方程的联立推导可得到，压缩腔内介质状态参数随螺杆转角变化的基本关系式为

(5)

控制容积内温度随螺杆转角的变化为

(6)

式中：h表示控制容积内工质的焓；v为控制容积内工质比体积；p为控制容积内工质的压力；θ1为螺杆转角；T为控制容积内工质温度；Vc为螺杆单个螺槽的最大控制容积.

以上模型的建立，压缩腔内的制冷剂包含了经济器补入的制冷剂气体，因此以上状态方程能够有效地表述补气过程的螺槽内的工质热力学状态参数.

2.2 经济器补气过程模型的建立与分析

由于经济器补气过程是一个边混合边压缩的过程，过程复杂，分析比较困难，因此本文以单螺杆压缩机几何型线以及常规圆形补气孔口为基础，采用喷管模型进行分析计算. 压缩机补气过程可假定服从一维流动的等熵压缩.

(7)

(8)

式中：p(θ1)表示压缩腔内压力随螺杆转角的变化；k为绝热指数；C为速度系数；AT(θ1)为补气孔口面积随螺杆转角的变化；pm为补气压力.

为了计算有效补气面积随螺杆转角的变化，可根据单螺杆螺槽型线与补气孔口结构进行分析. 单螺杆螺槽型线与圆形补气口位置关系如图3所示. 由于补气过程中补气的主流方向与补气孔的有效补气面积垂直，因此有效补气面积的计算应在补气主要流向的投影面上计算. 图3中齿前侧螺旋线VL在补气主流方向垂直的投影面上的方程为

(9)

齿后侧螺旋线VR在补气主流方向垂直的投影面上的方程为

(10)

补气孔口方程可以表述为

fc:(s-a1)2+(y-b1)2=r2

(11)

式中：yp1(θ2)表示齿前侧螺旋线在投影面上的y坐标，其方向与图3中y轴方向一致；xp1(θ1)表示齿前侧螺旋线在投影面上的x坐标；yp2(θ2)表示齿后侧螺旋线在投影面上的y坐标，其方向与图3中y轴方向一致；xp2(θ1)表示齿后侧螺旋线在投影面上的x坐标；θ1、θ2分别表示螺杆转角和星轮转角，且有θ1/θ2=11/6；R为螺杆和星轮半径；a为螺杆外边界到星轮中心的距离；b为星轮齿宽；r为补气孔口半径；a1、b1为补气口在投影面上的原点坐标.

齿前后侧螺旋线投影方程与补气口相切及相交时的交点可用表1表示.

随着螺杆转角的变化，齿前侧螺旋线投影方程与补气口的面积变化可用格林公式进行求解：

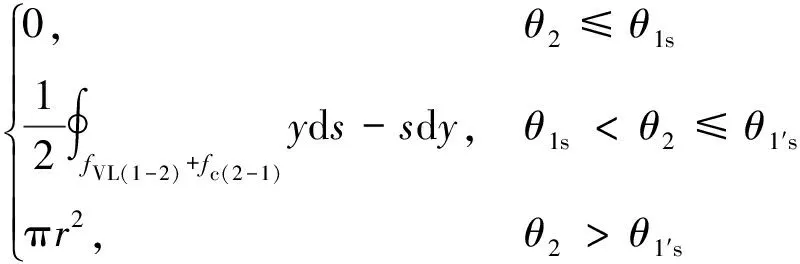
(12)

式中：θ1s为VL线与补气口开始相切时螺杆转角；θ1′s为VL线与补气口脱离时的螺杆转角.

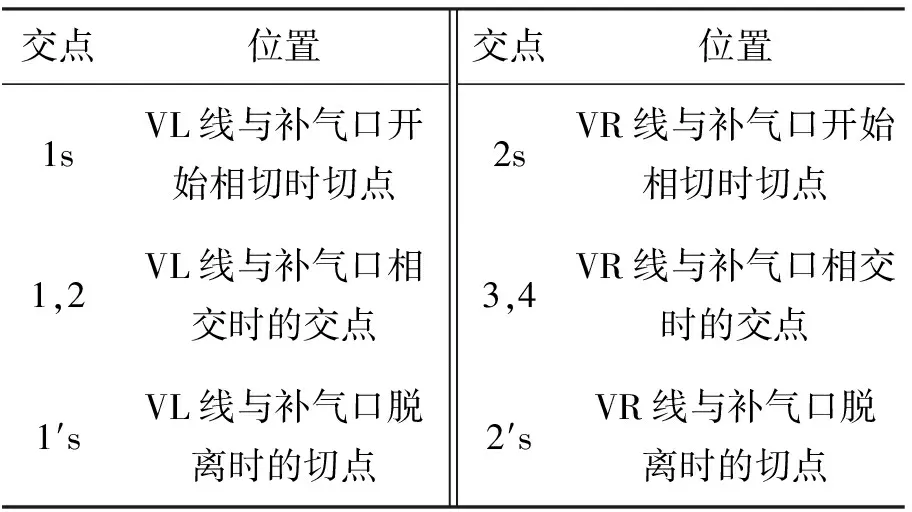
表1 螺旋线投影方程与补气口相切时交点

同样齿后侧螺旋线投影方程与补气口的面积变化可用以下方程求解：

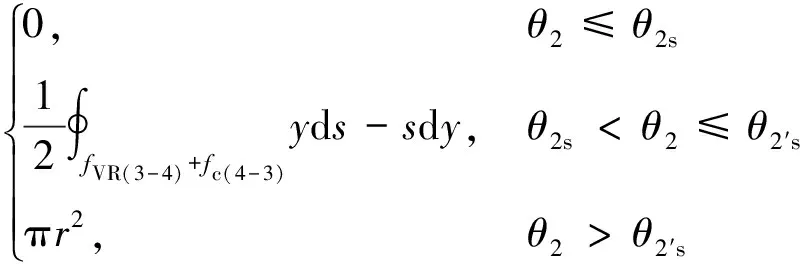
(13)

式中：θ2s为VR线与补气口开始相切时螺杆转角；θ2′s为VL线与补气口脱离时的螺杆转角.

有效补气面积随螺杆转角的变化可用如下方程表示：

(14)

冷凝器出口工质的质量流量qmd，流过经济器后分为两部分：一部分经过补气管路，再经补气口进入压缩腔的补气流量为qms；另一部分制冷剂流量qmk，通过主回路进入蒸发器再进入压缩机. 则补进压缩机的补气量可用相对补气量表示为

(15)

补气过程的压焓图如图1(b)所示，经济器采用的是闪发器，根据闪发器的能量平衡方程，可以得出闪发器能够供给的相对补气量即循环相对闪发量为

(16)

式中：h4表示冷凝器后工质的焓；h5表示膨胀阀b前工质的焓；hs表示闪发器出来的工质的焓.

由以上分析可知，当系统运行时只有当a1和a2相等时，系统才能达到稳定平衡状态，此时的中间补气压力为平衡态补气压力，即图1(b)中m点所对应的补气压力pm，本文采用二分法计算中间补气压力，计算开始时，可假定补气压力pm为进排气压力平均值，而后根据补气- 压缩过程的计算模型和闪发器的能量平衡方程式分别计算出a1、a2. 其主要逻辑关系流程图如图4所示.

由于在不同一级内压缩比下，其补气状态参数会有很大变化，一级内压缩比可表示为

(17)

式中：Vθ为单螺杆压缩机的最大基元容积；Vθn为开始补气时螺槽的基元容积.

机组的主要性能指标制热量可表示为

Qd=qmd(h3-h4)

(18)

压缩功的表示方程为

W=qmd(h3-hn)+qmk(h2-h1)+(qmk+qms)w2-n

(19)

其中边混合边压缩的补气过程的压缩功为技术功，可通过以下方程积分求得：

(20)

制热COP为

(21)

式中：h1表示压缩机进口工质的焓；h3表示压缩机出口工质的焓；hn表示补气结束后控制容积内工质的焓；W表示压缩过程所耗的总功.

3 计算结果及其分析

本文补气开始的一级内压缩比为1. 单螺杆压缩机的主要设计参数如表2所示.

表2 单螺杆压缩机主要设计参数

在计算各蒸发温度下，取定压缩机进气过热度为10 ℃；冷凝温度为46 ℃，选取制冷剂为R22为工质，其热力性质采用道宁拟合的马丁- 侯方程进行计算[27]. 计算暂不考虑螺槽之间的泄漏.

图5为压缩机单个螺槽内的质量随螺杆转角的变化，因为补气是从螺槽封闭就开始补气，所以从图中可以看出螺槽封闭时，补气介入，此时螺槽内的质量迅速增加，当容积在2.7×10-5m3时，此时也即是补气结束时，螺槽内的质量不再随容积的减小而变化，并且随着蒸发温度的增加，螺槽内的质量也在增加，这是因为蒸发温度增加时，进气密度增加，导致螺槽内制冷剂质量流量增加.

图6为螺槽内压力随容积的变化，图中可以看出随着压缩过程其压力逐渐增加，并且显示补气前后压力的变化率明显不同，说明补气过程对螺槽内压力变化影响较大. 蒸发温度越高，螺槽内气体越先达到排气压力，此时压缩机若没有滑阀调节以便及时排气，则压缩机会出现明显的过压缩损失.

图7为螺槽内制冷剂温度随压缩过程的变化，图中可以看出，温度的变化率在补气前后明显不同，不同蒸发温度下达到排气温度的数值和对应的螺槽容积也不同，蒸发温度越高，其达到的排气温度越小，分析认为蒸发温度高，此时的压比减小，因此排气温度减小.

由图8～10可以看出，随着蒸发温度的增加，常规无补气系统和经济器补气系统的制热量、压缩机功耗和系统COP都在逐渐增加. 但与常规空气源热泵系统相比，经济器补气系统的制热量、压缩机功耗以及系统COP均明显增加. 在假定条件下，蒸发温度在-30 ℃～0 ℃时，补气以后制热量相应地可提高19.3%～39.6%，其中蒸发温度越低，可提高的制热量越高，分析认为是因为蒸发温度越低，进气压力越低，其相对补气量越多. 此时功耗相对增加17.3%～32.1%，COP最高可增加19.7%.

由图9可以看出，常规热泵系统和经济器补气热泵系统的压缩机功耗随着蒸发温度的增加，其增加的趋势在逐渐变缓，分析认为随着蒸发温度的增加，达到同样的排气压力，其压比减小，因此其功耗的变化率减小.

4 结论

本文以闪发器为经济器补气形式，以单螺杆压缩机几何型线为基础，建立了能够更为全面的描述热泵系统补气过程的数学模型. 在假定条件下，计算了不同蒸发温度下螺槽内压力、质量以及温度随螺槽容积的变化规律，并与常规热泵进行了对比.

1) 在经济器补气条件下，补气结束时，螺槽内的内容积比为1.51，整个补气过程中，螺槽内的压力、温度和质量都迅速增加，当补气口封闭，即补气结束时螺槽内的质量趋于稳定，而后螺槽内的压力和温度随着压缩的进行继续升高，直到达到排气压力. 补气前后螺槽内的温度和压力的变化率明显不同，说明补气对螺槽内的热力参数影响较大.

2) 不同蒸发温度下，螺槽内制冷剂的热力参数明显不同，但其变化趋势具有较好的一致性. 并且蒸发温度越高，螺槽内制冷剂热力状态参数会越早达到排气状态.

3) 与常规热泵系统相比，经济器补气空气源热泵系统的制热量、压缩机功耗以及系统COP都会有明显的升高，蒸发温度在-30℃～0℃时，补气后制热量相应的可提高19.3%～39.6%，其中蒸发温度越低，可提高的制热量越高，此时功耗的增加量为17.3%～32.1%，在计算条件下，COP最高可增加19.7%.