基于粗糙集赋权的山区公路土石边坡可拓稳定性评价模型

乔建刚，孙希涛

(1.河北工业大学土木与交通学院，天津 300401； 2.天津市交通工程绿色材料技术工程中心，天津 300401)

近年来,边坡安全问题日益突出,尤其在山区,滑坡、泥石流等地质灾害频繁发生, 造成生命财产的损失，阻碍了交通建设的发展. 目前，国内外专家学者对边坡稳定性研究成果主要有，徐文杰等[1]在总结各研究成果的基础上，首次介绍了土石混合体；油新华等[2-3]以实验为基础，得出了边坡的含石量对边坡稳定性影响重大；孔德刚[4]的研究结果表明地形和边坡土体组成是破坏边坡稳定性的主要影响因素，而降雨则导致了边坡稳定性的破坏；Gray[5]的研究表明坡面形态对边坡的稳定性有很大的影响；Li[6]建立了边坡稳定性分析的模糊评价模型；Luo等[7]建立了边坡评价的支持向量机(support vector machine,SVM)模型；Zhou等[8]基于影响边坡稳定性因素的不确定性，提出基于模糊神经网络的边坡稳定性评价方法； 彭东黎等[9]、张士伦等[10]利用模糊分析方法，建立了边坡稳定性评价模型；冯晓等[11]首次把植被列入边坡稳定性的评价体系中去，并对边坡进行了稳定性评价；丁丽宏等[12]考虑到边坡稳定性影响因素的复杂性和影响因子的难确定性，以模糊物元理论为基础，评价了边坡的稳定性；文献[13-18]采用组合赋权模糊云理论对高边坡稳定性进行了评价. 综上所述，对边坡的稳定性研究成果较多，但是对山区土石边坡稳定性评价较少，且评价方法中指标权重值的确定多较为主观、不准确. 本文在实地调研山西山区公路土石边坡稳定性影响因素的基础上，建立山区公路土石边坡稳定性评价指标体系，采用粗糙集理论确定各指标权重，权重值的确定客观合理. 最后，采用可拓学评价模型来评估土石边坡稳定性. 以实际边坡进行验证，结果证明此评价方法科学、有效、合理.

1 边坡评价指标的选取及体系建立

在总结了现有国内外边坡稳定性研究成果的基础上,实地调研了山西省山区国省干线公路沿线土石边坡失稳破坏的特点，发现边坡失稳破坏是由降雨等原因造成的，因此评价指标未考虑地震等原因. 最终选取了影响边坡稳定性的4个一级指标和12个二级指标，如图1所示.

一级指标：水文气象A1；坡体状况A2；岩土体特征A3;植被状况A4.

二级指标：降雨量C1、渗流C2、地下水位C3；边坡坡度C4、边坡高度C5、边坡形态C6；基岩岩性C7、岩石占比C8、块石级配C9；植被类型C10、根系发育状态C11、植被覆盖率C12.

2 指标权重的确定

为使对边坡稳定性评价的结果准确，必须准确地确定各评价指标的权重值. 粗糙集理论以原始数据为依据，克服了人为主观确定权重的缺点，能真实地发掘出评价指标对边坡稳定性影响的重要程度，故选用粗糙集理论对指标权重进行确定.

利用粗糙集理论计算各评价指标的权重前，需要建立决策信息表. 决策表的形式为S=(U,C,D,V). 其中，U表示论域，是一个非空的有限集合；C是条件属性的合集，D是决策属性的集合. 其中C∩D=∅,D≠∅;V=C∪D表示属性值集合.

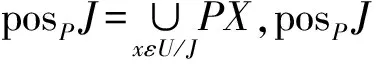
在粗糙集中，决策信息表S是这个信息系统所有的数据的集合，在决策信息决策表中，不同评价指标C的重要性是不一样的. 粗糙集理论可以判断某一个属性Ci被移除之后决策属性表S分类的变化情况. 如果一个属性Ci被移除之后，信息表分类发生了较大变化，就说明该属性Ci是个比较重要的属性；相反，则说明属性的重要性较低.

考虑不同指标原始数据值差别较大，为了便于数据处理，根据各评价指标的评价标准，赋予相应的分值区间，根据国家相关标准、行业规范以及现有研究成果，并结合山西省山区公路地质气候特点，对单因素指标进行量化，指标量化情况如表1所示.

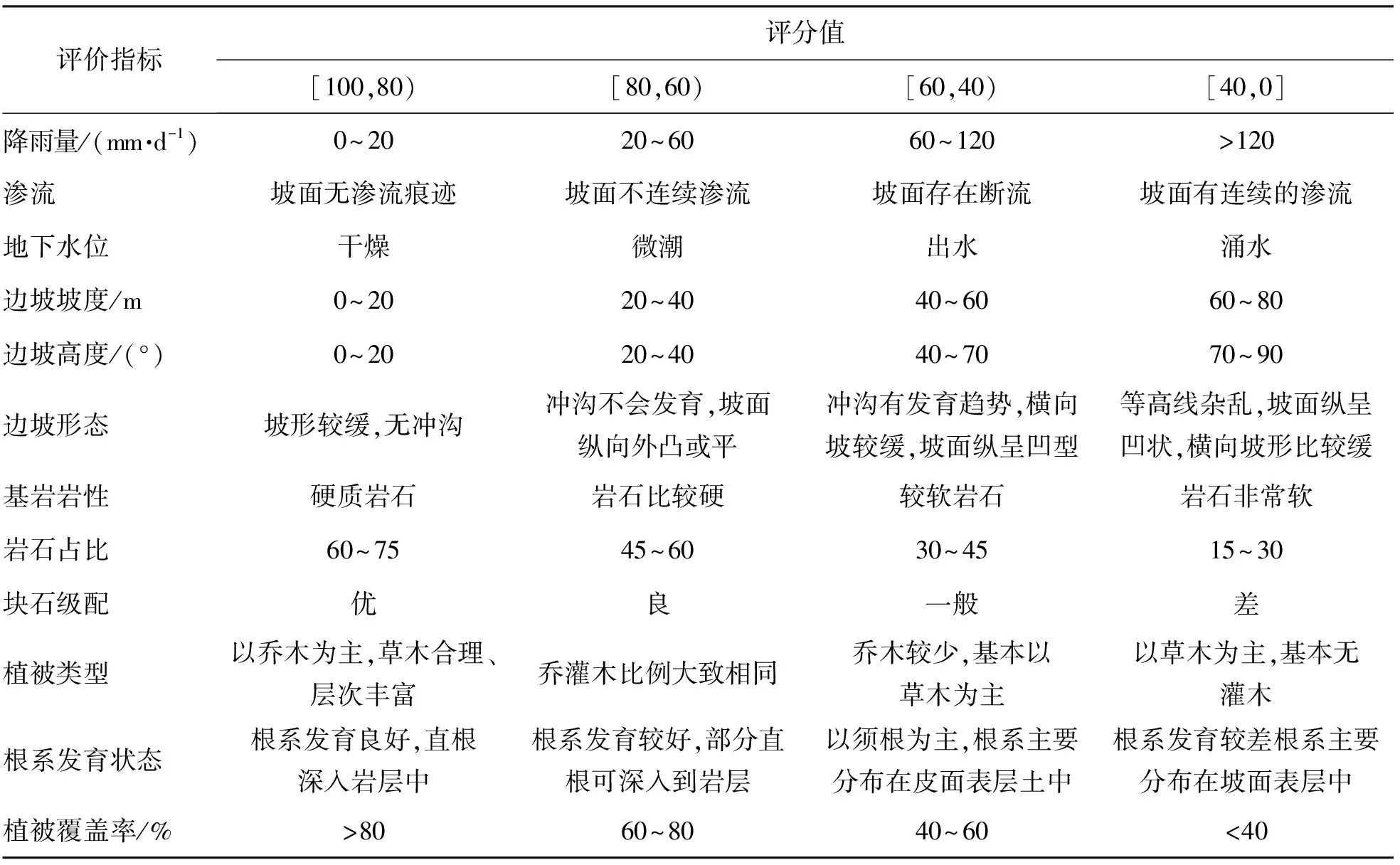
表1 指标及量化值

利用粗糙集理论，在计算评价指标权重时，需对指标数据进行离散化处理. 根据表1把边坡现状数据离散化处理，条件属性集{C}分为{Ⅰ，Ⅱ，Ⅲ，Ⅳ}4个等级，对应的分值范围为[100,80)，[80,60)，[60,40)，[40,0]. 根据边坡稳定性状况等级把决策属性集{D}划分为{Ⅰ，Ⅱ，Ⅲ，Ⅳ}4个等级，代表边坡稳定性状况的“一级、二级、三级、四级”.

二级指标条件属性集{降雨量C1、渗流C2、地下水位C3；边坡坡度C4、边坡高度C5、边坡形态C6；基岩岩性C7、岩石占比C8、块石级配C9；植被类型C10、根系发育状态C11、植被覆盖率C12)用C={C1,C2,C3,C4,C5,C6,C7,C8,C9,C10,C11,C12}表示. 对调查的山西15处边坡数据进行离散化处理，得到的结果如表2所示.

根据粗糙集理论，各指标对应的等价类及正域为

表2 边坡稳定性等级二级指标评级决策表

U/D={{u1,u3,u9,u14},{u2,u10,u12},

{u4,u5,u8,u11,u13,u15},{u6,u7}}

U/C={{u1,u2,u3,u4,u5,u6,u7,u8,u9,

u10,u11,u12,u13,u14,u15}}

U/C1={{u1,u2,u4,u5,u6,u7,u9,u11,u12,u13,u15},

{u3,u14},{u8,u10}}

其余类似不再赘述.

U/{C-C1}={{u1,u2,u3,u4,u5,u6,u7,
u8,u9,u10,u11,u12,u13,u14,u15}}

其余类似不再赘述.

posCD={{u1,u2,u3,u4,u5,u6,u7,u8,u9,
u10,u11,u12,u13,u14,u15}}
posC-C1D={{u1,u2,u3,u4,u5,u6,u7,u8,
u9,u10,u11,u12,u13,u14,u15}}

其余类似不再赘述.

各个指标的重要度计算公式为

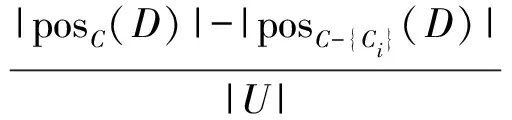
(1)

sig(Ci,C;D)代表了条件属性Ci在条件属性C集中的重要性，但是不能体现系统中条件属性Ci自身的重要性，而条件熵法可弥补这一缺点，因此用定义条件熵的方法来解决这一问题，条件属性C相对于决策属性D的条件熵为

(2)

则每个二级指标的权重计算公式为

(3)

通过式(1)～(3)求出边坡各评价指标的权重，C1，C2，C3，C4，C5，C6，C7，C8，C9，C10，C11，C12的权重值分别为0.164、0.108、0.046、0.101、0.093、0.221、0.057、0.047、0.010、0.042、0.029、0.082.

指标权重的合理性检验：

为检验评价指标的权重分配是否合理，需要计算出评价指标的权重熵. 权重熵值计算公式为

(4)

计算得出评价指标体系的指标权重熵值H=0.972，在(0.5，1)内，因此，说明指标体系权重分配是合理的.

3 山区土石边坡可拓稳定性评价模型

3.1 可拓学理论简介

可拓学理论，最初是由中国广东工业大学的蔡文等教授在1983年创立的学科，可解决多种参数混合但是没有相容的矛盾系统问题. 目前，已被推广应用到各大学科[19].

可拓学理论是以物元为基本元素的，假设P是需要被评价的系统，其中有n各物元存在这系统中，分别用R1,R2,…,Rn表示. 用三元组R=(N,C,V)来表示物元，其中N是需要评价的事物，C则是被评事物的评价指标，V代表指标等级值. 一个事物N中，如果有n个评价指标，每个评价指标的取值为V1,V2,…,Vn，则把R叫作n维物元，山区土石边坡可拓稳定性评价模型计算流程如图2所示.

3.2 山区土石边坡可拓稳定等级

本文将山区土石边坡稳定性状况等级划分为稳定、较稳定、稳定性一般、不稳定4个等级，具体划分如表3所示.

表3 边坡稳定性等级划分

根据可拓物元的理论，分别用N={N1，N2，N3，N4}表示.

1) 根据表1、山区土石边坡稳定性评价等级的建议值以及

(5)

可确定土石边坡评价的经典域. 式中：RI表示一个物元；NI表示第I个评价类别；CI为第I个评价指标；VI则表示第I个评价指标的取值范围，用VI=〈aI1,bI1〉来表示. 经典域就是评价等级相对应的评价指标的取值范围.

2) 确定待评价系统的节域,表达式为

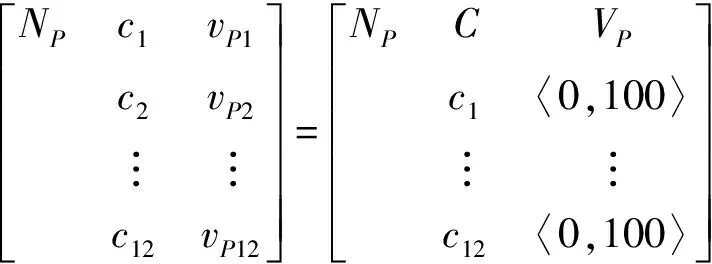
(6)

式中：RP为需要评价系统的节域；NP为评价等级；vpi为第i个指标Ci在RP中的取值范围，vpi=〈api,bpi〉. 节域表示需要评价事物指标总的取值范围.

3) 确定待测物元

(7)

式中：Ri为需要评价的物元；Ni为需要评价事物；Xi则表示为需要评价事物的在第i个评价指标内的具体数值.

4) 利用关联函数，得出各评价指标的关联度

根据可拓学原理，关联函数表示物元属于某其中一个等级程度的量化指标，这体现了物元量变以及质变的过程. 评价指标对于评价等级的关联度为

(8)

其中，

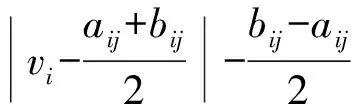
(9)

5) 确定综合关联度，确定评价等级

用Kj(vi)表示二级评价指标计算得到的关联度，结合计算得到的评价指标的权重wi，待评价土石边坡的综合关联度Kj(q)为

(10)

根据得到的各评价评价指标的综合关联度Kj(q)，如果KS(q)=maxKj(q)，评价结果为S级.

3.3 可拓安全评价模型的建立

根据上面评价指标权重的确定，运用可拓学理论以及可拓学评价方法，本文建立了山区公路土石边坡可拓稳定性评价模型，如图3所示.

4 模型应用

某山区国道沿线LK0+375，土性为土石复合型边坡，坡面为东北西南走向，地层岩性为较硬岩，垂直高度为42 m，平均坡度为34°，坡面有不连续渗流，边坡表面潮湿，边坡含石量45%，所在地区温带大陆性季风气候区，历史日降雨量为90 mm. 植物种类仅有2种小灌木，且根系发育一般，根系分布于表层稀土中，植被覆盖率为35%，坡面为东北西南走向，边坡长度为340 m.

将以上边坡数据进行整理，并根据式(6)用物元模型把待评价系统的指标数据表示出来. 然后按式(5)～(9)计算得到各二级评价指标的关联度，如表4所示.

根据式(10)可以计算得到边坡的综合关联度，N1，N2，N3，N4的关联度分别为-0.350 99、-0.068 72、0.091 68、-0.237 57.

可以得到，综合关联度最大为0.091 68，因此，土石边坡稳定性等级为Ⅲ级，应对其采取适当的加固技术护坡. 利用文献[20]的方法，求得此边坡的稳定性等级也为Ⅲ级，均与实际边坡相符，验证了该评价模型的合理性.

表4 指标关联度

5 结论

1) 本文综合考虑了影响土石边坡稳定性的各个因素，构建山区公路土石边坡稳定性评价指标体系，利用粗糙集确定了各评价指标权重.

2) 用可拓学评价模型对山区公路土石边坡稳定性进行了评价，并以实际边坡进行验证，结果表明该模型评价结果科学、合理、实用性强. 为以后山区土石边坡稳定性的评价提供了参考.