车辐式索桁架温度响应试验及可靠性评估

刘占省，王竞超，韩泽斌，薛素铎，王泽强，张维廉

(1.北京工业大学建筑工程学院，北京 100124； 2.北京市建筑工程研究院有限责任公司，北京 100036)

车辐式索桁架结构是一个由索桁架、环索和刚性受压环梁组成的自平衡体系. 根据已建工程的测试结果[1]，考虑温差±25 ℃时有30～50 MPa的预应力变化，因此，研究温度变化对结构的影响对结构安全使用至关重要. 张爱林等[2]以鄂尔多斯索穹顶结构为研究对象，分析了其在温度和预应力一起作用下结构的力学性能；范重等[3]对温度变化导致的国家体育场结构的内力变化进行了分析，并提出相关措施；郭妍[4]研究了不同温度对某大跨钢结构的影响效应；Arezki等[5]研究了温度变化对索桁架桥体系的影响；Liu等[6]研究了弦支穹顶结构施工过程中温度变化对结构的影响，并提出了一个新的施工预应力控制简化计算公式；郭彦林等[7]研究了施工环境温度对车辐式张拉结构成型后索力的影响，提出了3种消除温度影响的措施. 上述关于温度作用对索穹顶、弦支穹顶等张拉结构的影响做了一些研究，但是考虑温度变化对服役期间的车辐式索桁架影响的研究较少.

本文以一跨度为6 m的车辐式索桁架结构模型为研究对象，当结构张拉成型后进行三维扫描，获取修正理论有限元分析模型，将修正理论有限元模型的结果定义为修正值. 通过试验值、理论值与修正值的对比，分析车辐式索桁架的温度响应. 最后，基于可靠性理论进行可靠性分析，研究温度变化对本结构可靠性的影响规律.

1 模型设计

本试验以某车辐式索桁架结构工程为背景，几何缩尺比例为1∶10，应力比为1∶1. 具体缩尺情况可参考文献[8-11].

此结构试验模型由10榀径向索、上下环索、外环梁和柱子组成，试验模型如图1所示. 试验模型构件规格可参考文献[12-13].

拉索索力的测点位置为上、下径向索的1、3、5、7、9榀，有10个测点，上、下环索各布置1个测点，索力测点共12个. 测点布置情况如图2、3所示.

2 获取修正模型

将加工完毕的结构构件及节点进行组装，通过调节拉索的长度进行结构预应力的施加，进而将结构张拉成型，张拉完毕后的结构如图4所示.

当结构张拉成型之后对结构进行三维激光扫描，利用点云模型、建筑信息模型(building information modelling，BIM)将有限元分析模型进行修正，试验中所用三维扫描仪器如图5所示，点云模型如图6所示.

如图7所示，根据点云模型建立修正的BIM，在修正BIM中提取新的关键节点坐标，利用新的关键点坐标将Ansys分析模型的关键点坐标进行更新，得到修正有限元分析模型.

3 温度响应分析

考虑温差的影响，取构件温度变化范围为-50～50 ℃，活荷载取0.167 kN/m2，与正常使用荷载为同一个量级. 通过调节各个构件的调节套筒来模拟温度对本结构的影响，试验调节拉索长度可参考文献[11].

3.1 位移分析

将试验模拟的不同温度下、结构下节点位移的理论值、修正值的计算结果进行对比分析.

如图8～10所示，A-A轴对应1榀与6榀温度上升时，节点位移下降，当温度为50 ℃时位移下降最大. 当温度下降时，节点位移上升，当温度为-50 ℃时位移上升最大. 升温引起的结构位移比降温明显. 当温度变化时，受温度影响较大的节点为外撑杆节点与中撑杆节点.

3.2 索力分析

温度变化时结构索力变化如图11～20所示.

1) 上径向索索力变化量

由图11～14可知，上径向索索力变化量随温度的变化成线性关系，温度上升时上径向索索力下降. 当温度为50 ℃时，索力降低幅度最大，约为40%. 理论值、修正值与实测值的相差较小.

2) 下径向索索力增量

由图15～18可知，下径向索索力变化量随温度成线性变化，温度下降时下径向索索力下降. 当温度为50 ℃时，索力降低最大，约为30%.

3) 环索索力变化量

由图20、21可知，同上、下径向索相同，环索索力随温度线性变化，温度下降使环索索力下降. 当温度为50 ℃时，索力降低最大，其中上环索索力下降约为40%，下环索索力下降约为30%.

4 温度变化可靠性分析

4.1 可靠度分析

假设此结构的材料为理想弹塑性，荷载工况取1.0恒荷载+1.0活荷载，考虑不同温度变化对结构的影响.

构造本结构以位移控制的功能函数

g=[u]-umax

(1)

式中：umax为结构中竖向位移绝对值的最大值；[u]为规定的位移变形限值. 不同标准下的最大位移输出变量如表1所示，其中L为车辐式索桁架跨度. 本文具体可靠度分析方法以及随机变量可参考文献[14-17].

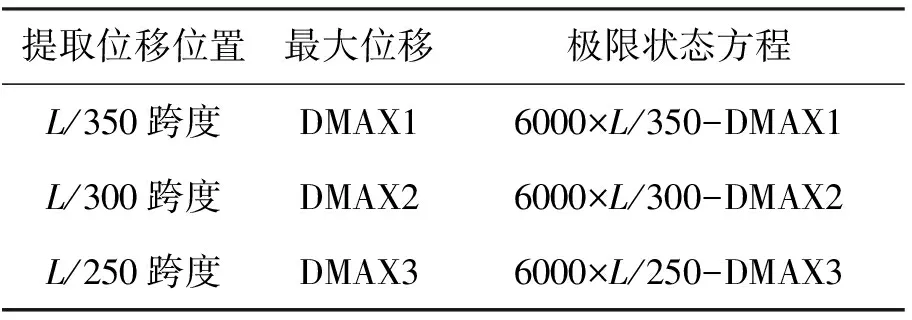
表1 不同标准下的最大位移输出变量

通过分析得到不同位移限值控制下的可靠指标，由图21可知，随着温度升高，结构位移限值DMAX1、DMAX2、DMAX3的可靠指标逐渐减小，并且大致成线性变化，温度越高，结构安全性越低. 由于DMAX1、DMAX2、DMAX3只是定义不同的极限状态方程的输出变量，不影响结构本身性能，所以可靠性指标随温度变化较为一致. 结构可靠度在不同位移限值下，其可靠性指标为0～3.7，满足结构正常使用极限状态下可靠度指标.

针对以上数据，拟合出不同位移限值下可靠指标方程.

DMAX1位移限值下温度- 可靠度指标拟合方程为

y=-0.020 7x+1.017 4

(2)

DMAX2位移限值下温度- 可靠度指标拟合方程为

y=-0.023 0x+1.604 4

(3)

DMAX3位移限值下温度- 可靠度指标拟合方程为

y=-0.025 5x+2.472 6

(4)

式中：y为可靠度指标；x为上径向索温度变化值.

4.2 灵敏度分析

分析随机输入的变量对DMAX2的灵敏度，提取出的具体灵敏度数值如表2所示. 由表可知，下径向索预应力(PREJ1)与活荷载(D2)的灵敏度数值较大，表明当结构受温度影响时下径向索预应力对结构位移的影响较大.

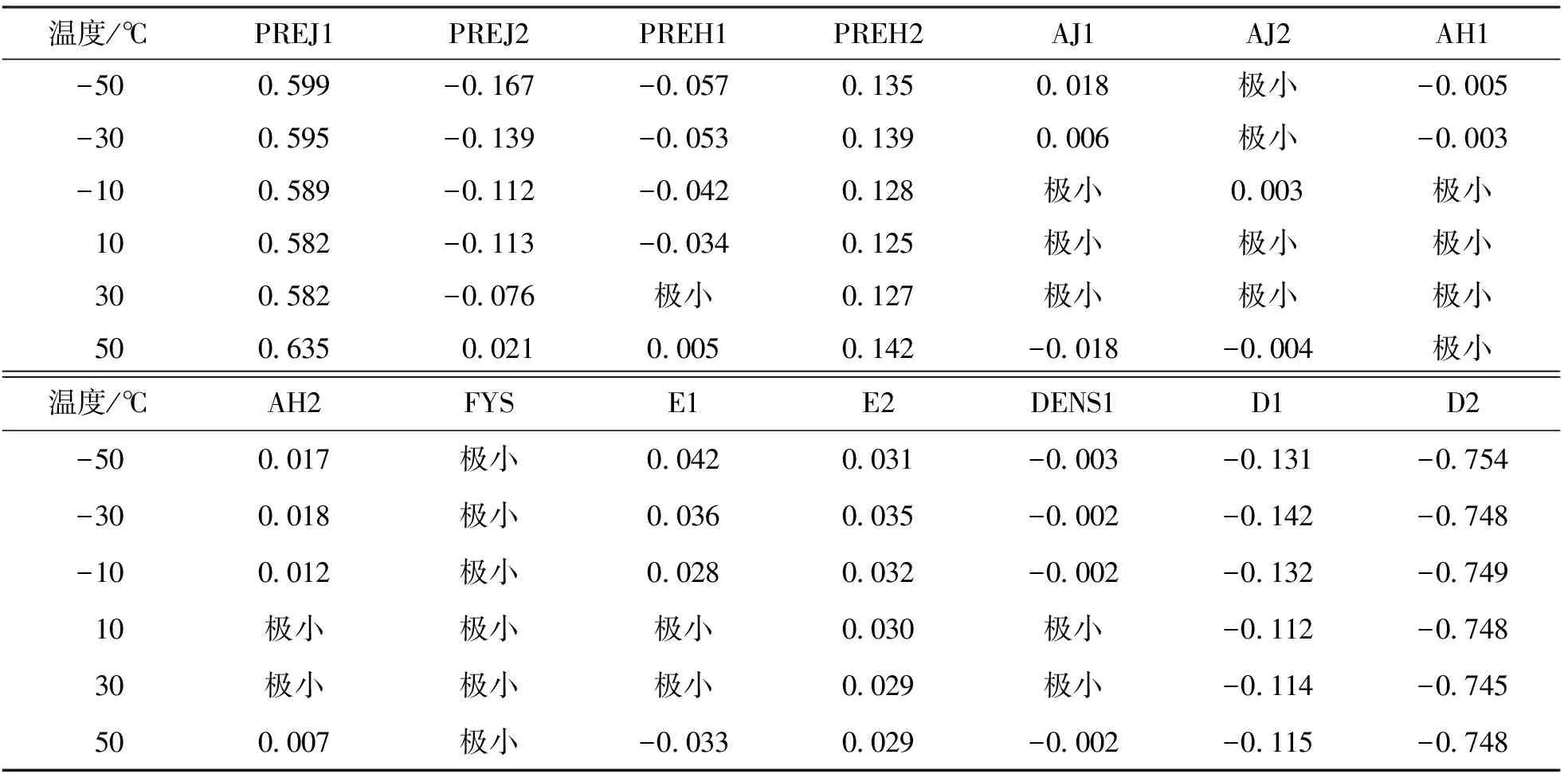
表2 温度影响下随机输入变量的灵敏度

注：PREJ1、PREJ2分别为上、下径向索预应力；PREH1、PREH2分别为上、下环索预应力；AJ1、AJ2分别为上、下径向索截面积；AH1、AH2分别为上、下环索截面积；FYS为拉索强度平均值；E1为撑杆的弹性模量；E2为拉索的弹性模量；DENS1为拉索密度；D1为恒荷载；D2为活荷载.

4.3 可靠度分析验证

将缩尺模型等比放大100倍，得到与实际工程的相似模型，验证缩尺模型可靠性分析的正确性.

1) 可靠度验证

对实际模型进行不同温度下的可靠性分析，得到实际模型不同温度下的最大位移限值1/300可靠度，并将其与缩尺模型可靠度进行对比，如图22、表3所示.

由图22可知，缩尺模型与实际模型随温度变化的可靠指标变化趋势相同，变化率基本一致. 由表3

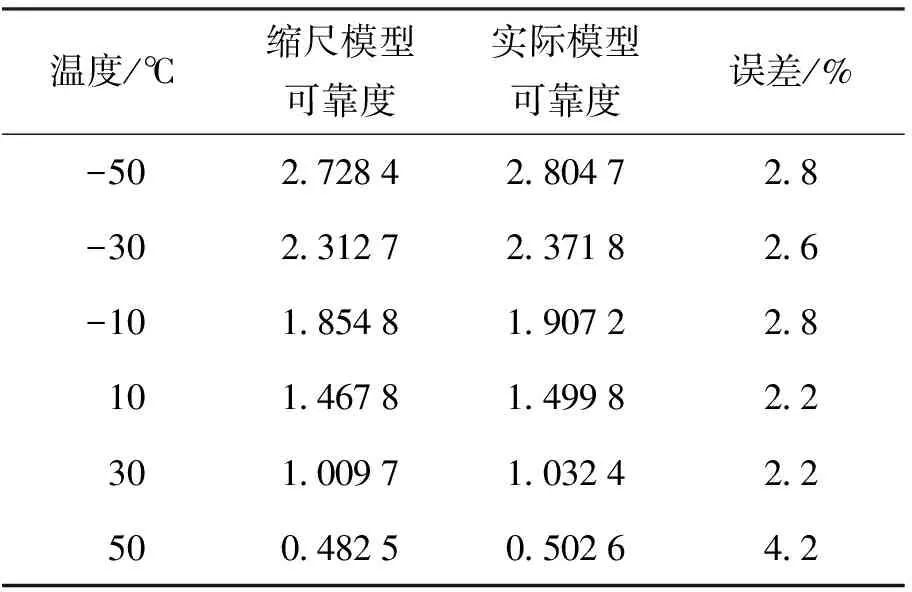
表3 可靠指标误差

可知，由实际模型得到的可靠度略大于缩尺模型可靠度，最大误差为4.2%. 因此，对缩尺模型进行的可靠性分析对实际工程具有参考性.

2) 灵敏度验证

取30 ℃的工况，对扩大之后的结构模型进行灵敏度分析，得到扩大之后的模型在不同温度下的最大位移限值l/300灵敏度，与缩尺模型的灵敏度对比结果见图23.

由图23可知，在温度30 ℃时，PREJ1和D2对结构位移影响较大. 当考虑实际模型时，位移限值的影响因素会增多，但影响都很小.

5 结论

1) 以0 ℃作为结构服役期间基准温度，当温度达到50 ℃时，节点最大竖向位移可达-10 mm，当温度达到-50 ℃时，节点最大竖向位移可达5 mm，车辐式索桁架结构节点位移对温度升高更为敏感.

2) 温度作用对车辐式索桁架结构拉索内力的影响不可忽略，在温度影响下，上环索与上径向索、下环索与下径向索索力的变化量基本相同，且上部索力变化较大，对温度变化更敏感.

3) 本结构的可靠度随温度的上升而不断下降，下径索施加的预应力和活荷载的线性相关系数最大.