基于变异粒子群算法的局部阴影光伏阵列MPPT 研究
2020-05-27沈攀,付波
沈 攀,付 波
(湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室 电气与电子工程学院,湖北 武汉 430068)
0 引言
随着化石能源的日渐枯竭,太阳能作为一种清洁可再生能源越来越受到广泛关注。在局部阴影情况下,光伏阵列的P-U特性曲线有多个极值点,此时传统的MPPT 算法就会失效[1]。
针对这个问题,国内外许多学者做了大量的研究。文献[2-4]利用神经网络来进行MPPT 控制,神经网络具有很强的学习能力,经过一定的学习之后,可以直接根据环境参数预测出光伏阵列的最佳工作电压。文献[5-6]利用粒子群算法来进行最大功率点跟踪,避免了算法陷入局部极值寻优。
考虑到多极值光伏阵列的复杂性,本文提出一种基于变异粒子群算法的MPPT 控制策略,通过引入变异机制来增强算法的全局寻优能力,避免算法陷入局部极值。与传统的MPPT 算法相比,本方法跟踪精度更高,过程更平稳,提高了局部阴影情况下光伏阵列的能量利用效率。
1 光伏电池模型及输出特性
1.1 光伏电池数学模型
为研究光伏电池的输出特性,通常将光伏电池用一个由电流源、二极管、并联电阻、串联电阻组成等效电路来模拟,如图1 所示。
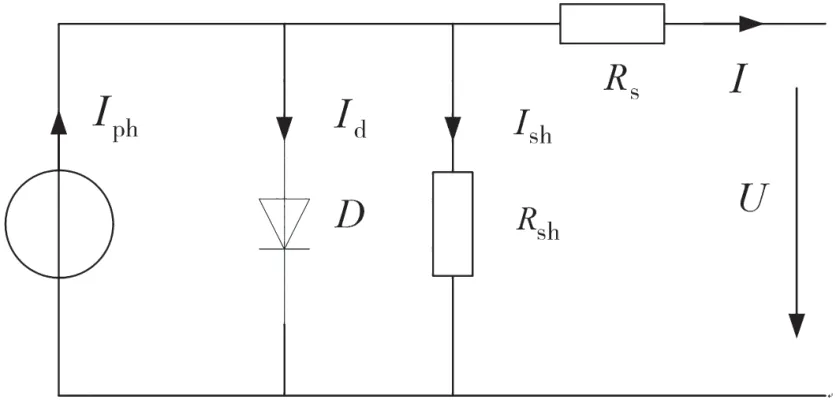
图1 光伏电池等效电路
其中,Iph表示电流源电流,D 为反并联二极管,Rs和Rph分别表示光伏电池的串联电阻和并联电阻。光伏电池输出电流的数学方程为:
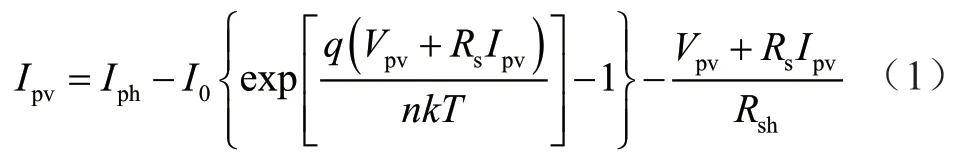
其中,I0为二极管反向饱和电流,Iph为光伏感应电流,k为玻尔兹曼常数,n为二极管理想因子,T为光伏电池温度,q为电子荷电常数。
1.2 阴影情况下光伏阵列输出特性
由于单块光伏电池输出功率较小,为满足需要通常将光伏电池通过串联以及并联构成光伏阵列。当光伏阵列所受光照强度均匀时,光伏阵列的P-U特性曲线为只有一个极值的单峰曲线。当处于阴影情况时,光伏阵列所受光照不均匀,此时光伏阵列的P-U特性曲线呈现出多个极值点,其中只有一个极值点为全局最大功率点,其余极值点为局部极值点。
图2 表示的是一个由3 块光伏电池串联组成的光伏阵列在不同光照情况下的P-U特性曲线。无阴影情况下,光伏阵列所受光照强度均为1 000 W/m2,局部阴影情况PSC1:光照强度依次为[1000、600、200]W/m2,局部阴影情况PSC2:光照强度依次为[1000、500、500]W/m2。
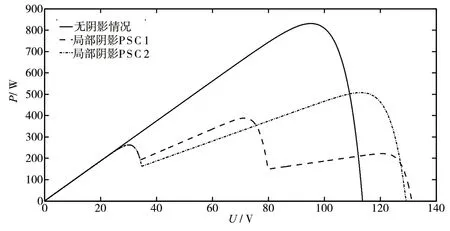
图2 不同光照情况光伏阵列P-U 特性曲线
2 光伏阵列MPPT 算法
2.1 扰动观测法
扰动观测法是一种传统的MPPT 算法,具有原理简单、易于实现等优点,其基本流程如下。
步骤一,测量光伏阵列当前时刻的工作电压U0和输出功率P0。
步骤二,对当前工作电压施加一个扰动量ΔU,使其工作在Ut,输出功率为Pt。
步骤三,判断扰动后的输出功率Pt与扰动前的输出功率P0的大小。
步骤四,若Pt大于P0,则继续往相同方向施加扰动,否则往反方向施加扰动。
虽然扰动观测法简单易实现,但其最大功率点跟踪性能受步长影响很大。当步长较大时,光伏系统输出功率会产生很大的波动。当步长较小时,算法跟踪速度慢且容易陷入局部极值点,不能准确跟踪到全局最大功率点。
2.2 粒子群算法
粒子群算法(PSO)是一种经典的智能优化算法,它能通过粒子的不断迭代实现全局寻优。PSO 中的粒子具有位置和速度两个属性,在迭代的过程中,粒子的位置由当前粒子的历史最优位置Pi和种群的历史最优位置Pg实现更新。第t+1 次迭代时,粒子i的速度和位置根据如下公式更新:
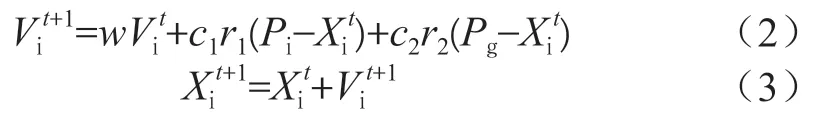
其中,w为惯性权重,c1、c2为学习因子,r1、r2为(0,1)的随机数。
2.3 变异粒子群算法
本文将变异机制引入粒子群算法中,提出一种变异粒子群算法。当粒子按式(3)更新其位置后,对更新后的位置进行变异,若粒子变异后的位置优于,则粒子位置更新为变异后的位置,否则不变异。粒子位置按式(4)进行变异:

本文通过对粒子群算法进行变异,显著增强其跟踪全局最大功率点的能力,提高了算法的全局寻优性能。变异粒子群算法的流程如图3 所示。
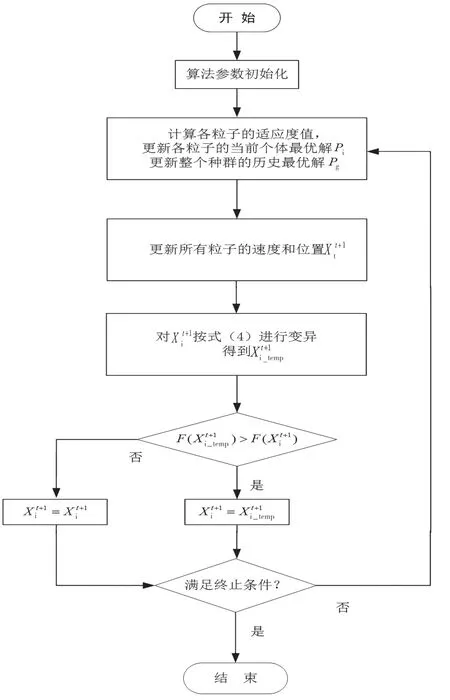
图3 变异粒子群算法流程图
3 仿真及结果分析
为验证本文所提变异粒子群算法的有效性,在理论分析的基础上进行Matlab/Simulink 仿真,光伏MPPT系统基于Boost 电路,如图4 所示。Boost 电路的主要参数为:C1=10 μF,滤波电感L=1 mH,母线电容C2=100 μF,负载电阻R=20 Ω,开关频率fs=10 kHz。
光伏阵列采用3 块光伏组件串联而成,在光照强度为局部阴影PSC1 时,光伏阵列的P-U特性曲线呈现出三个极值点的情况,如图2 所示。其中,全局最大功率点为:388.5 W,其余两个局部极值点分别为263 W 和221.6 W。在局部阴影PSC1 下,对基于Boost电路的光伏MPPT 系统分别采用变异粒子群算法和扰动观测法进行仿真对比,算法中粒子数目为6,粒子初始位置在解空间中均匀分布,初始变异步长为1/2 的解空间长度,其结果如图5、图6 所示。
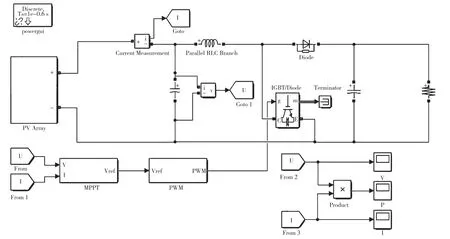
图4 基于Boost 电路的光伏MPPT 系统
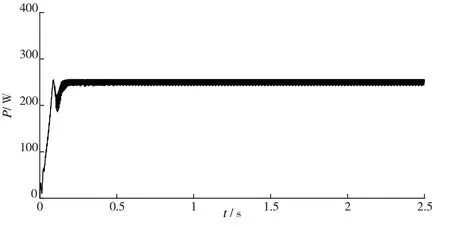
图6 局部阴影PSC1 情况下扰动观测法功率跟踪曲线
由仿真结果可以看出,变异粒子群算法在1.1 s 时准确地跟踪到了全局最大功率点388.3 W,功率输出波动较小,与最大功率点真实值388.5 W 相比,相对误差为0.05%。扰动观测法控制下,在0.21 s 时跟踪到的功率为262.8 W 并且存在较大的波动,对比图2 可知扰动观测法陷入了第一个局部极值点。与扰动观测法相比,本文提出的变异粒子群算法在光伏阵列局部阴影情况下输出功率波动小,跟踪精度更高。
4 结论
局部阴影情况下,传统的MPPT 算法不能准确地跟踪到全局最大功率点。为了减小能量损失,本文在粒子群算法的基础上引入变异机制,提出一种变异粒子群算法并用于光伏阵列的MPPT 控制。通过仿真分析可以得出如下结论。
(1)本文提出的算法在局部阴影情况下具有良好的全局寻优性能,并且跟踪过程更加稳定,功率波动更小。
(2)局部阴影情况下,传统的MPPT 算法不能准确地跟踪到全局最大功率点,本文提出的算法比传统的MPPT 算法具有更好的控制效果。
