基于粒子群-支持向量机(PSO-SVM)的苯储罐泄漏事故风险预测
2020-05-26程云芳
程云芳,邱 榕
(中国科学技术大学火灾科学国家重点实验室,合肥,230026)
0 引言
苯是种常见的有毒危险化学品,被广泛应用于各种工业场所[1]。一旦苯储罐发生泄漏事故,若未采取对应预防应急措施,会对人们的生命、财产、环境等带来严重伤害。有必要在事故发生前,对苯储罐泄漏事故进行风险预测减少苯储罐泄漏事故的发生。
目前众多学者已对苯储罐泄漏事故的风险预测进行了大量研究,并提出多种评价方法[2],如事故树分析法、层次分析法、灰色理论法、模糊综合评价法、事故后果模拟等,这些方法主要通过定性、定量相结合的方式,找到苯储罐泄漏事故中潜在的致险因素。但由于苯储罐泄漏事故风险评价是一个动态过程,当其中某些潜在危险因素变化时,这些评价方法不能迅速调整,难以在事发前预测苯储罐泄漏事故的风险程度,极大影响评价效率。而支持向量机SVM是种机器学习算法,能进行快速计算,并且在处理非线性、小样本等问题具有独特优势[3]。因此,我们提出将SVM模型运用于事故前苯储罐泄漏事故风险预测。为使其模型性能最优,我们采用全局优化算法粒子群(PSO)优化SVM模型参数,建立PSO-SVM风险预测模型。在进行风险预测过程中,首先通过建立预测指标体系、确定指标权重获取预测样本数据。为验证PSO-SVM模型风险预测性能,我们分别采用遗传算法(GA)和网格搜索法(GS)优化SVM参数,并比较测试集与PSO-SVM、GA-SVM、GS-SVM三种模型预测结果的均方误差及相关系数,然后进一步探讨了PSO-SVM中权重调整方式、种群规模对模型预测性能的影响。研究发现权重线性递减所建PSO-SVM模型预测值与测试集相关系数更高、均方误差更小、预测效果更好。
1 获取风险预测样本数据
1.1 建立风险预测指标体系
引发苯储罐泄漏事故的危险源是各不同系统的危险因素所组成的复杂系统,为合理有针对性地预测苯储罐泄漏事故的各潜在风险,建立的苯储罐泄漏事故风险预测指标体系必须科学地、全面地分析各指标和系统之间的关系、及各指标内在的相互关系。因此所有指标选取,必须严格遵循独立性、科学性、可操作性和动态性原则[4]。
通过调研目前国内外的苯储罐泄漏事故,结合事故致因理论、危险源理论,可从人机环管四方面将苯储罐泄漏事故风险预测指标体系,划分为4个一级指标和14个二级指标,如图1所示。

图1 苯储罐泄漏风险预测指标体系
1.2 明确指标权重
本文采用层次分析法确定上述14个苯储罐泄漏事故二级指标的权重值,层次分析法是一种可将复杂因素定性判断问题转化为定量计算各因素权重值的方法,最早在上世纪70年代由Saaty[5]提出,可有效决策、判断各种复杂问题的主要影响因素。
层次分析法通过构造判断矩阵,然后对判断矩阵进行一致性检验,来明确各指标的权重值。此次苯储罐泄漏事故风险预测指标体系构造的判断矩阵,是通过问卷调查形式,由5位专家结合自身经验和专业能力,采用数字1~9为标度,对所有指标进行两两比较,再进行打分而确定。其中标度1~9所对应的各含义,如表1所示。

表1 标度含义
采用MATLAB软件对各指标因素的最大特征值λmax、一致性比率、权重值分别进行计算,然后进行判断矩阵一致性检验,计算结果分别如表2~表6和图2、图3所示。

表2 一级指标判断矩阵和一致性检验

表3 人员因素的判断矩阵和一致性检验

表4 设备因素的判断矩阵和一致性检验

表5 管理因素的判断矩阵和一致性检验

表6 环境因素的判断矩阵和一致性检验

图2 苯储罐风险预测指标体系一级指标权重值

图3 苯储罐风险预测指标体系二级指标权重值
1.3 计算样本数据
为形成苯储罐泄漏事故样本数据,本文将上述苯储罐泄漏事故风险预测体系中所有指标的参数值,根据不同风险程度,采用满分制将其依次划分成5个级别,依次为:危险性非常高(0,20],危险性比较高(20,40],危险性一般(40,60],危险性比较低(60,80],危险性非常低(80,100]。并利用软件 MATLAB在5个不同风险等级区间内各随机生成4组数据,共随机生成20组不同风险程度的评语集数据。根据1.2,可知预测指标体系所有指标权重值wi,再结合公式(1),可得出20组不同随机数据依次所对应的苯泄漏事故风险程度值,计算如(1)所示。
(1)
式中,Si为第i组数据得到的苯泄漏事故风险程度值;wi为第i个指标权重值;aji表示j组数据第i个指标的风险程度值。
为进一步预估苯储罐泄漏事故风险值,我们将上述20组随机数据和其一一对应的苯泄漏事故的风险程度值,作为风险预测模型样本数据,如表7所示。同时将样本数据按3∶1原则,依次划分为训练集数据、测试集数据。则样本数据前面15组为训练集数据,主要用于训练PSO-SVM模型;样本数据后面5组为测试集数据,用于检验PSO-SVM模型性能。最后将PSO-SVM预测模型所需要的样本数据存入EXCEL中,在进行PSO-SVM模型训练时,利用MATLAB依次读取EXCEL所存入的样本数据。

表7 苯储罐泄漏事故风险预测模型的样本数据
2 建立苯储罐泄漏风险预测模型
2.1 建立粒子群-支持向量机(PSO-SVM)模型
支持向量机作为机器学习算法,在处理非线性关系方面拥有独特的优势。通过非线性映射可将复杂非线性问题转化成高维空间中的线性回归问题,能够快速地对多因素间复杂关系进行学习分析[6]。支持向量机(SVM)回归预测模型的本质就是根据有限的样本数据,考虑每个输入和输出样本之间复杂交叉关系,寻找到它们之间的最优关系,并对测试集中的输入样本给出合理的输出,其结构示意图如图4所示。

图4 SVM结构示意图
SVM回归函数可表示如下:
Y=w.φ(Ai)+b
(2)
式(2)中w为权值向量,b为偏差,A是输入样本数据集,Y为预测值。其中A={x1,x2,…,xi;y1,y2,…,i=1,2,3,…},x1,x2,…xi和y1,y2,…,均为样本输入量。
对非线性问题,引入核函数K(z,zi),通过非线性映射φ(Ai),将输入空间转化为高维空间,非线性问题变为线性问题,则优化的目标函数表示为:
(3)
利用拉格朗日乘子和对偶原理求解上式的ω,则有:
(4)
得到最终的回归函数为:
(5)

为使SVM模型预测性能最优,我们需要对其内部参数惩罚因子C、核函数参数g进行优化[7]。粒子群(PSO)种全局优化算法,主要通过种群粒子之间的竞争、合作共同实现种群进化[8]。我们采用PSO对SVM模型的惩罚因子C和核参数g进行参数寻优,构建PSO-SVM模型示意图如图5所示,主要步骤如下:
(1) 将样本数据分为训练、测试两大类,然后归一化处理所有样本数据;
(2) 使用粒子群算法优化种群参数,同时设置种群规模、惯性权重因子、迭代次数等各项参数;
(3) 计算粒子适应度值,然后更新粒子速度、位置等参数。粒子适应度值越小,代表此时粒子位置最优;
(4) 判断最优参数的结束条件,主要看迭代次数能否满足设定值或适应度值是否达到设定数值,若达到,优化算法结束;否则,参数优化继续;
(5) 将寻找到的最优参数C、g分别代回SVM回归模型,然后训练样本数据;
(6) 通过测试集数据测试PSO-SVM回归预测性能,如果预测值符合设定要求,输出预测数值;否则,持续优化参数C、g,至预测数值符合设定值。

图5 PSO-SVM模型示意图
2.2 确定苯储罐泄漏风险预测模型的输入与输出
我们将模型的输入变量确定为上述苯储罐泄漏的主要风险因素,并将各随机数据所对应的风险数值确定为模型输出量,建立PSO-SVM苯泄漏风险预测模型,如图6所示。在计算前,我们归一化处理预测模型的样本数据,同时将样本数据限制在[0,1]之间。

图6 苯储罐泄漏风险预测模型的输入与输出
2.3 寻优过程参数设置
在采用PSO-SVM模型进行风险预测时,选用默认的RBF核函数,并依次设置算法参数值。终止迭代次数设置为200,种群规模数量设置为20,学习因子c1设置为1.5,c2设置为1.7,惩罚因子C设置为区间(2-8,28),权重值w设置为1,核函数参数g∈(2-8,28),其他设置为默认值。为验证基于PSO-SVM的苯储罐泄漏事故风险预测模型性能,分别建立GS-SVM、GA-SVM风险预测模型,依次采用网格搜索法GS、遗传算法GA优化SVM模型参数。GS-SVM模型参数寻优中,最小步长设为0.8,其余参数和PSO-SVM模型一致。GA-SVM模型参数寻优中,参数和PSO-SVM模型参数设置一致。
3 分析预测结果
依次采用PSO-SVM、GS-SVM、GA-SVM三种风险预测模型,在MATLAB平台上训练20组苯储罐泄漏事故样本数据。种群粒子通过迭代进化得到最优粒子,最优粒子所对应的最佳适应度值即为所寻最佳参数C、g的数值。在种群粒子迭代进化中,设置最佳适应度值为样本数据交叉验证均方差值。三种风险预测模型的参数优化结果,分别如图7~图9所示。

图7 PSO-SVM参数优化结果
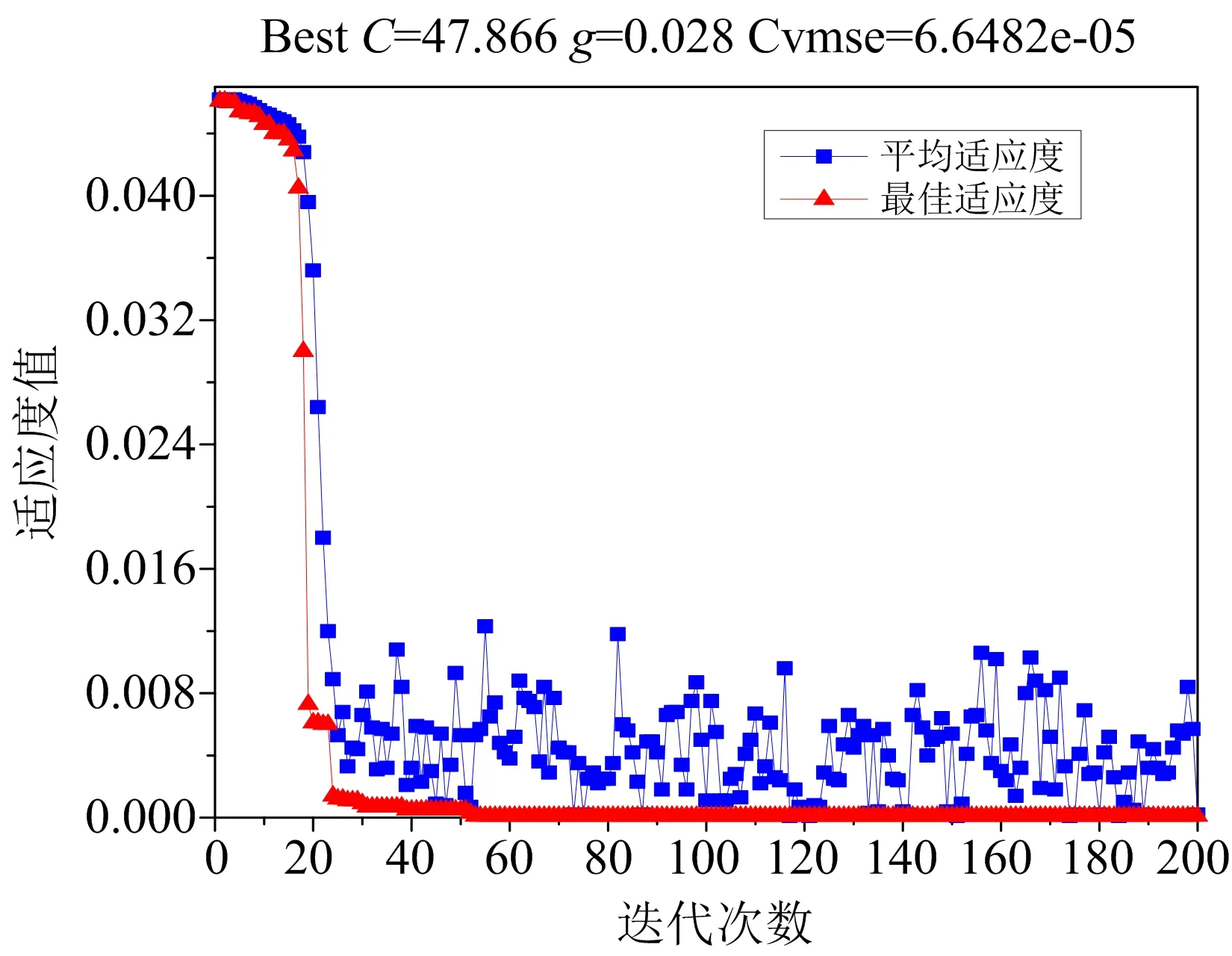
图8 GA-SVM参数优化结果

图9 GS-SVM参数优化结果
从图7~图9可知,PSO-SVM模型参数优化过程中,粒子迅速迭代得到最佳适应度值,并长时间稳定,此时寻找到最佳参数C、g值依次为5.271、0.01,最小交叉验证均方差值7.0796E-05。GS-SVM风险预测模型进行参数优化过程时,得到最小交叉验证均方差值5.4434e-05,此时的最佳位置BestC=0.125,Bestg=256。GA-SVM模型参数优化过程中,种群粒子经过53次迭代后,得到最佳适应度值,此时相对应的最佳参数C、g数值依次为47.866、0.028。比较三种预测模型的适应能力,可知PSO-SVM预测模型的适应度值最小,则适应能力最好。三种预测模型优化得到的最优参数C、g数值,依次代入各模型进行风险预测。预测过程中,三种模型分别训练前15组样本数据,通过训练形成回归预测模型,然后对后5组(编号16~编号20)样本数据进行预测。三种模型的回归预测结果如表8所示,三种模型预测结果效果图如图10所示。

表8 三种模型预测风险值与计算值对比

图10 三种预测模型风险预测效果图
由表8、图10可以得知:
PSO-SVM模型预测效果最好,回归预测的风险值与测试样本数据最吻合;GA-SVM模型回归预测的风险值趋势和测试样本数据基本一致,但预测风险值偏差要高于PSO-SVM模型;GS-SVM模型回归预测的风险值趋势完全不同于测试样本数据,预测效果最差。
GS-SVM模型中,预测的4组风险值基本一致,且存在较大偏差,说明GS-SVM模型具备较差泛化能力,不能根据测试样本数据的输入给出合理输出,主要原因可能为:网格搜索法最优参数寻找过程中,没有搜索到种群最佳位置,寻找到的参数并非最佳解,从而构建的GS-SVM风险预测模型存在一定偏差。
为进一步表征PSO-SVM风险预测模型的性能,依次计算了三种模型的均方误差MSE值、线性相关系数R2,计算结果如表9所示。
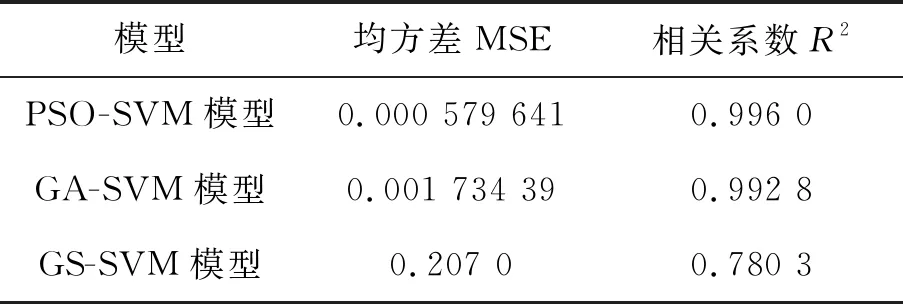
表9 三种预测模型MSE和R2对比
由表9可知:三种模型中,PSO-SVM模型预测的风险值与样本数据的相关系数达到0.996 0,相关性最高,同时PSO-SVM模型的最小MSE值为0.000 579 641,说明PSO-SVM风险预测模型的性能最好。
4 预测结果讨论
由上述预测结果,可知PSO-SVM风险预测模型性能最优,可适用于苯储罐泄漏事故的风险预测。但其他参数如权重值、种群规模也可能会影响 PSO-SVM模型的风险预测值,下面将重点进行讨论。
4.1 权重值对PSO-SVM预测结果的影响
权重值会影响粒子群PSO算法的优化性能,常用的权重调整方式为权重线性递减、权重随机分布和权重自适应这三种[9]。为验证权重值的影响,依次建立三种权重调整方式的PSO-SVM风险预测模型,计算中将最小权重值设置为0.4,最大权重值设置为0.9。三种权重调整方式和权重为常数所建PSO-SVM模型的风险预测效果,如图11所示。

图11 不同权重调整方式对预测结果影响
由图11可知:四种模型所预测的风险值趋势和测试样本数据基本相同,但权重线性递减所建PSO-SVM模型预测效果更好,所预测的4组风险值和样本数据最吻合。因此,建立PSO-SVM风险预测模型时,优先将权重值设置为线性递减方式,以实现预测效果最优。
4.2 种群规模对PSO-SVM预测结果的影响
种群规模会影响粒子群算法的优化效率[10],因此分别讨论了1~20的种群规模对PSO-SVM风险预测模型的影响,计算结果分别如表10、图12所示。

表10 不同种群数量预测风险值的MSE、R2对比

图12 不同种群数量的时间消耗
由表10、图12可知:不同种群规模的PSO-SVM模型不影响最终所预测的风险值,所预测的风险值的相关系数、均方差完全一致;然而,种群规模会影响PSO-SVM风险预测模型的计算时间。种群规模为1时,计算时间较种群规模为2~4之间所用时间多;种群规模为2~20时,随着种群规模变大,计算时间也明显增多。这说明种群规模过大计算用时会增多,种群规模较小计算用时也会较长,可能是由于种群规模较小,参数寻优过程不易搜索到种群最优解,从而使得计算用时较久。因此采用PSO-SVM模型进行风险预测时,需要进行多次计算,选择最佳种群规模,以达预测模型效果最优。
5 结论
采用粒子群-支持向量机(PSO-SVM)模型进行苯储罐泄漏事故的风险预测。首先通过建立预测指标体系、确定指标权重获取预测样本数据。其次通过确定苯储罐泄漏事故风险预测的输入、输出量,建立了基于粒子群-支持向量机(PSO-SVM)的风险预测模型。
为验证PSO-SVM模型风险预测性能,分别对比了PSO-SVM、GS-SVM、GA-SVM三种预测模型的风险预测值、相关系数及均方误差,发现PSO-SVM预测模型的相关系数最高、均方差最小,说明PSO-SVM风险预测模型效果最好,这为苯储罐泄漏事故的风险预测提供了新的方法。
最后进一步探讨了PSO-SVM风险预测模型中权重调整方式、种群规模对模型预测性能的影响。发现权重线性递减所建PSO-SVM预测值与测试样本数据最吻合,预测效果最好;种群规模不会影响PSO-SVM风险预测模型预测值,然而会影响预测过程的计算时间,种群规模过大或者过小都会影响计算时间,需要经过多次计算选择恰当种群规模数量。
