考虑双向群组运动特征的场域模型研究

杨潘云，傅丽碧，方 捷，刘宇星

(福州大学土木工程学院，福州，350116)

0 引言

随着经济增长，各类娱乐场所数量逐年攀升，大型综合性商场琳琅满目，吸引大量行人聚集。行人聚集使安全问题突出，行人动力学的研究可为火灾等紧急情况下的安全疏散研究提供理论支撑。群组作为行人流中重要的组成部分[1,2]，在行人动力学研究中不可忽略。与独立行人相比群组行人的运动特征更为复杂，群组行人不仅需考虑与周围环境的相互作用，还需考虑同组成员之间的相互牵绊。属于同一组的成员总是寻求以相同的速度和偏移角度移动[3,4]，以确保行走的舒适性和连贯性，其存在对速度、流量有明显的负面影响[3,5,6]。

不同规模群组在行走过程中呈现不同的构型。对于双人组而言，行走构型主要为肩并肩并列行走，该构型在单向及双向流的可控实验中进一步得到证实[7,8]，在双向流中双人组行人为减少与对向行人的摩擦会出现拉链效应，呈现错位行走的构型[7]，成员之间的距离则随着密度的增加逐渐减小。三人组的构型主要为“V”字形[2,9]，该构型及前后行人之间的距离不会随密度的变化而发生改变[9]。四人组在行走时呈现“U”字构型[2]。在高密度情况下，为减小与对向行人的冲突，三个或三个以上的群组会分裂单独的个体或双人组等小群体[2]。

已有学者将群组的运动特征考虑进行人模型中，构建了介观模型、微观模型[6,10-13]等。从这些模型中学者总结了一些现象，如合适的领导和稳定的团队组成有助于减少疏散时间，减少与办公室内障碍物的碰撞[6]，疏散过程中的行人横向移动可能会被垂直分组阻塞[13]等。在考虑群组运动特征的微观模型中，Wang等[14]考虑了行人在运动过程中的转向、避障、惯性等因素来构建群组场模型，以再现群组运动特征。部分学者将群组成员划分为领导者及跟随者[6,10]，领导者有绝对的领导权，仅考虑周围环境及行人的影响，跟随者服从于领导者的决策。但对于大群组而言，与群组中某一位成员维持较近距离较为困难。领导者的概念在模拟双人组行走特性时效果较好，但在模拟三人组、四人组等较大群组时存在一定的局限性。由此可见，涉及群组行人的动力学研究具有现实意义，仍需要深入探究。本文基于前人对群组行人运动特征研究的基础上，对群组场进行拓展，并引入预测场进行双向行人流研究。

1 模型构建

1.1 原始场域模型

场域模型[15]由蚁群行为特征启发而来，模型中介绍了静态场、动态场两种基本势场。静态场与周围环境相关，反应的是行人寻找最短路径到达目的地的期望，在模拟过程中始终不变。动态场与周围行人运动轨迹相关，反应的是行人的跟随作用，会随着时间的推移进行扩散和衰退。除此之外为避免与周围行人或障碍物发生碰撞，该模型还考虑了格子是否被行人占据及是否存在障碍物的问题。Kirchner和Schadschneider[15]依据以上假设制定的行人转移概率公式见公式(1)：

pij=Nexp(kDDij)exp(kSSij)(1-nij)ζij

(1)

式中：N：归一化参数，N=[∑exp(kDDij)·exp(kSSij)(1-nij)ζij)]-1；kD：动态场敏感性参数；kS：静态场敏感性参数；Sij：与距离相关的静态场；Dij：与周围行人运动轨迹相关的动态场；ζij：障碍物参数，若为障碍物则取0，否则为1；nij：行人占据参数，若该位置被行人占据则为1，否则为0。

静态场可以使用欧式距离计算：

(2)

其中(iTs，jTs)为目的地元胞坐标，(il，jl)为测量区域内所有的元胞坐标，(i，j)为计算时的元胞坐标。

动态场Dij是一个随时间变化的参数，如蚂蚁留下的化学轨迹那般会随时间的推移而向周围扩散及自身产生衰退，Nishinari等[16]将公式进行量化：

(3)

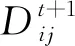
1.2 模型改进

1.2.1 考虑群组凝聚力

场域模型中一个分支即为考虑群组运动特征的研究[10,11,17,18]，如Müller等[18]将群组行人分为领导者及跟随者，领导者遗留下来的波尔粒子m>1，作用于同组行人，领导者不受其他领导者的影响，而跟随者受到领导者的影响。Qiu和Hu[19]在建立群组行人模型时，将群组凝聚方式分为两种，分别模拟了行人并列行走及跟随领导者行走的构型。魏晓鸽[20]定义群组成员倾向于向群组重心靠拢或跟随群组中走在最前方的行人，依此提出了群组中心生成法、群组领导者生成法。由此可见，在群组重心或领导者位置处存在的凝聚力点，能使群组成员凝聚在一起。

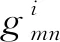
(4)

(5)

式中xmn和ymn分别代表格点(m，n)的X坐标和Y坐标。xi-sourcecell、yi-sourcecell为i群组重心的X坐标和Y坐标。

使用上述方法的模拟场景中，无法保障群组在运动过程中构型的稳定性，特别是对于四人组来说，受同组行人影响而处于不稳定状态情形较多。例如，图1(a)中为三人组，该构型无法满足1号行人往正前方行走的空间需求，虽然是与群组保持较近的距离，但不是稳定的构型。图1(b)、图1(c)中为四人组，该构型能够满足成员维持联系及移动所需空间，往重心方向靠近的行为反而会增加同组成员之间的冲突，因此4号、8号行人会选择往正前方行走而不是为了要走在群组在重心位置而选择往重心方向靠近。

按照日常生活经验及学者的理论研究[2,20,21]，在行人运动过程中，群组构型会有一定的震荡现象，而非严格的肩并肩行走，当该形态足以维持群组交流等需求时，会以该形态行走，图2～图4为结合前人研究结果[2,20,21]总结出的群组部分稳定构型示意图。

(a)图为不稳定构型，(b)、(c)为稳定构型

图2 双人组部分稳定构型

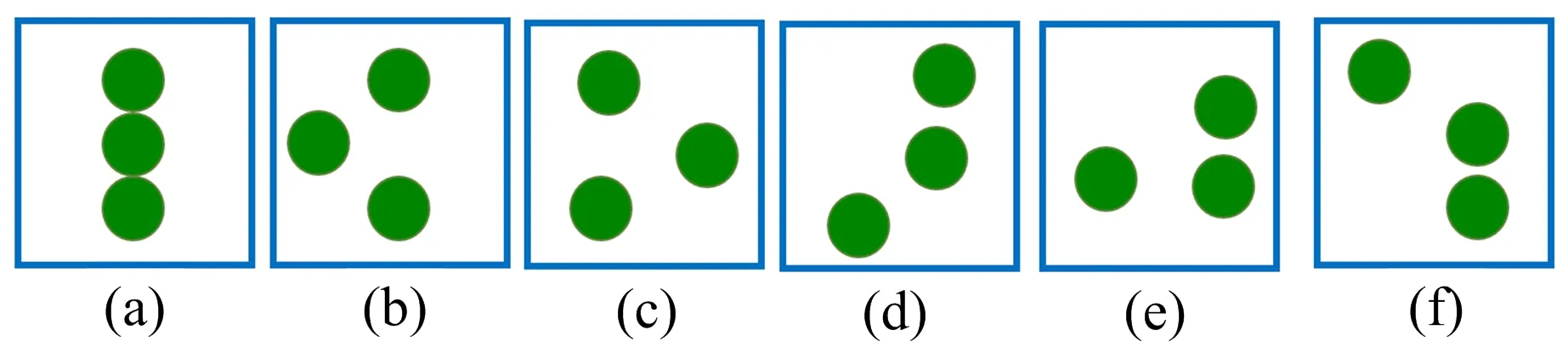
图3 三人组部分稳定构型

图4 四人组部分稳定构型

由此可见，群组成员不会无限地向群组重心靠近，因此本文引入预判距离阈值，改进成员无限靠近群组重心的机械性问题，使行人能以维持较近距离的相对稳定构型行走。我们给定预判距离阈值，当距离小于该阈值时则不再考虑群组场。

大群组在行走过程中比较容易分成小群组[17]，因此本文将四人组的群组重心进行偏移，在行走方向上向左向右移动0.5格，划分为两个小重心，靠近原群组重心右方的行人使用右方偏移的重心，靠近左方的行人使用左方偏移的重心。以图5(a)为例，上方两个行人在原群组重心位置的上方则使用向上偏移的群组重心，下方两个行人则使用向下偏移的群组重心。

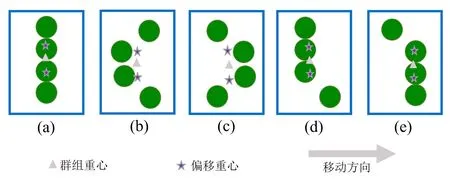
图5 重心偏移示意图

1.2.2 考虑群组避让行为

(6)

式中：Np：预测区域内反向行人总人数；Npg：预测区域内反向行人中不同规模群组总人数，下标g表示群组的规模，取1时为单人组，2为双人组以此类推；ε：群组规模影响权重值(见表1)；Sp：距离阻力影响权重值(见图6、图7)。

群组规模的大小影响着行人的避让决策，在有足够空间避让行人时，独立行人倾向于主动避让群组行人。群组规模越大，较小的群组避让大群组的意识也越强。基于以上假设本文依据群组的规模赋予群组不同的权重值。

表1 群组规模影响权重值

存在冲突的行人之间的距离是行人避让决策的考虑因素，发生冲突的行人之间距离越近压迫感就越明显，本文依据对向行人到预判位置的距离来确定距离阻力影响权重值。图6、图7为非后退及后退情况下距离阻力影响权重值的取值情况示意图，行人运动方向为从左往右，其中虚线圆为t时刻行人位置，实线圆为t+1时刻行人预判位置，浅灰色的区域为预判区域，预判区域为3×5元胞。

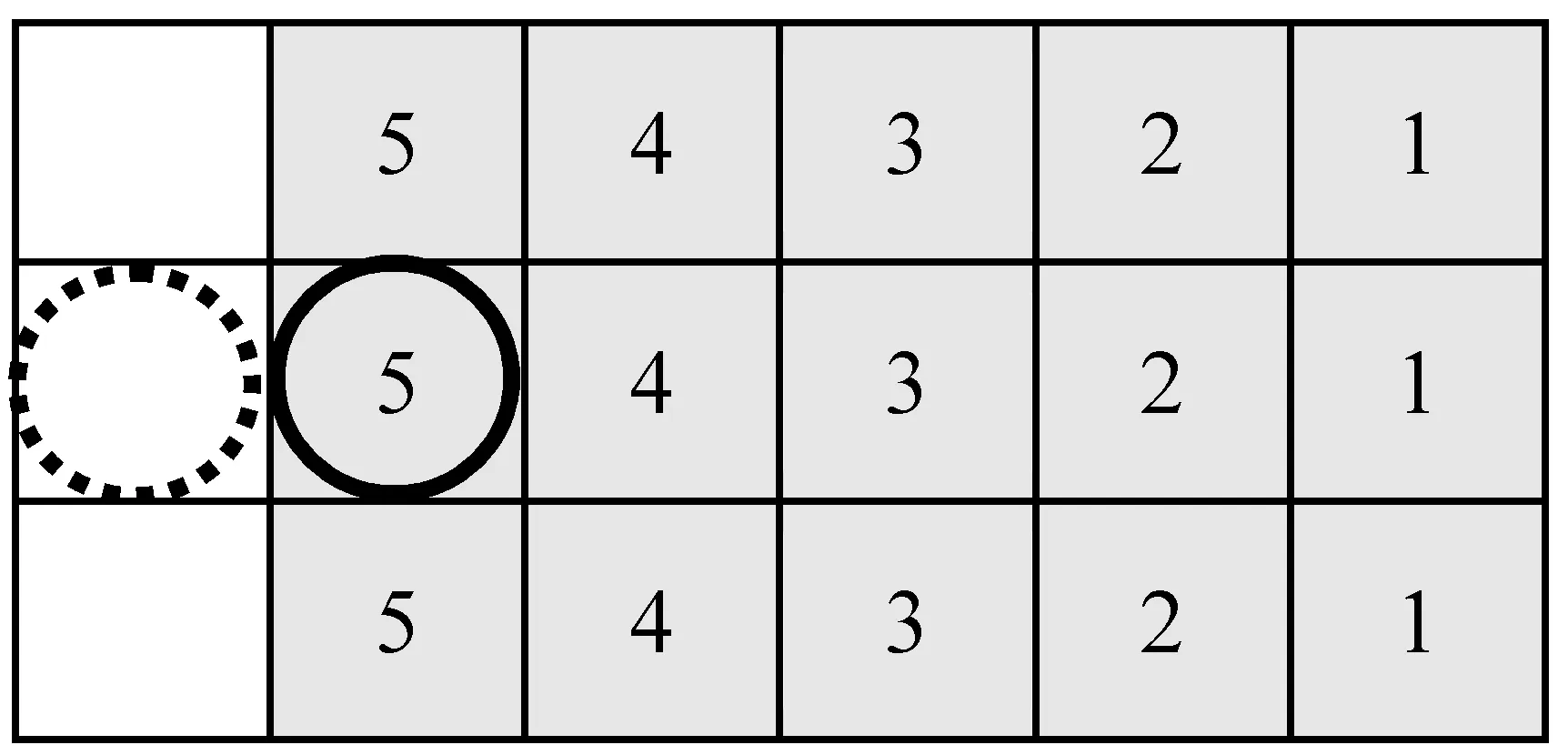
图6 非后退情况下距离阻力影响权重值

图7 后退情况下距离阻力影响权重值

1.2.3 拓展的群组模型

本文使用有后退的摩尔邻居，行人可往8个方向运动或维持原位不动，具体见图8。行人在行走过程中一般不会选择往斜对角行走及后退，因此本文将5、6、7、8方向的静态场进行削弱处理，并采用不会连续后退两步的后退模式。经过多次试验，当5、6、7、8方向的静态场值为1、2、3、4方向的0.5倍时，能减少同组成员之间的冲突，维持稳定的行走方向，因此本文5、6、7、8方向的静态场为1、2、3、4方向的0.5倍。

将预测场与群组场考虑进原始场域模型中构建概率转移公式(7)：

qij=Nexp(kSSij+kDDij+

(7)

其余参数含义与基本场域模型相同，具体见公式1。

图8 对行人周围9个位置进行编号，0为行人占据位置

模型的框架如图9所示，行人每一时间步的转移概率均由静态场、动态场、预测场、群组场共同决定。由转移概率预先判断移动的方向。在无冲突或竞争成功，且不是连续后退两步时往预判方向移动，否则保持原位不动。依此循环至模拟结束。

2 模拟结果与分析

2.1 模拟场景

为寻找符合行人运动特性的模型参数，对上述模型进行双向流通道场景下的情景模拟。通道长为L，宽为W，每个格子采用0.4 m×0.4 m的大小。密度为通道内行人总数除以通道面积。四人组、三人组、双人组、单人组是行人流中的主要组成部分[1,2]，因此本文仅研究这几类群组，如图10所示，初始时行人在通道两端随机产生。

2.2 参数选取

图11为在静态场及群组的协调作用下模拟得到的平均速度。模拟场景为6×24个格子的循环通道，通道中设置有双向行人，两端行人均为等比例的单人组、双人组、三人组、四人组，总共有80人，每个场景模拟十次，每次实验模拟5 000个时间步。模拟发现静态场对速度具有积极的影响，而群组场则为消极影响。当速度在0.8以上时群组构型稳定性不佳，速度小于0.3时往目的地行走意识弱。因此本文模拟参数ks取值为3.5，kg取3。

Kirchner和Schadschneider[15]提到：在kS取1.0、10的情况下，kD均可以在取1时达到最小值。α、β取不同值的情况下kD亦可在取1时达到最小值，因此本文将动态场敏感性kD参数取值为1，α、β均取0.3。

图9 拓展场域模型框架

图10 通道场景示意图

图11 kS及kg协调作用下的速度分析

本文依据行人行走过程中需要的前行空间，即移动空间需求确定预判距离阈值。研究发现男、女性平均步幅分别为66.6 cm、60.6 cm[22]，因此本文的预判距离阈值取值在1～2个元胞之间，又由于行人往正前方移动时，发现成员落后的反应时间比较迟钝，因此正前方的预测距离阈值较其他方向大。在使用预判距离阈值的模拟中，以从左往右行人为例，正前方即2方向(从右往左行人则为4方向)的预判距离阈值四人组、三人组为2元胞，单人组、双人组为0元胞，其余方向的预判距离阈值四人组、三人组、双人组均为1个元胞。

2.3 无干扰时的群组运动轨迹图

图12为无干扰情况下的群组运动轨迹图，在仅考虑静态场、动态场、群组场对群组的影响场景下能够很好地模拟行人在无干扰(无对向行人冲突)下的群组并肩行走的运动特征。按照日常生活经验及学者的理论研究[2,20,21]，在行人运动过程中，群组构型会有一定的震荡现象，模拟中双人组出现的轻微震荡现象符合群组运动特征。

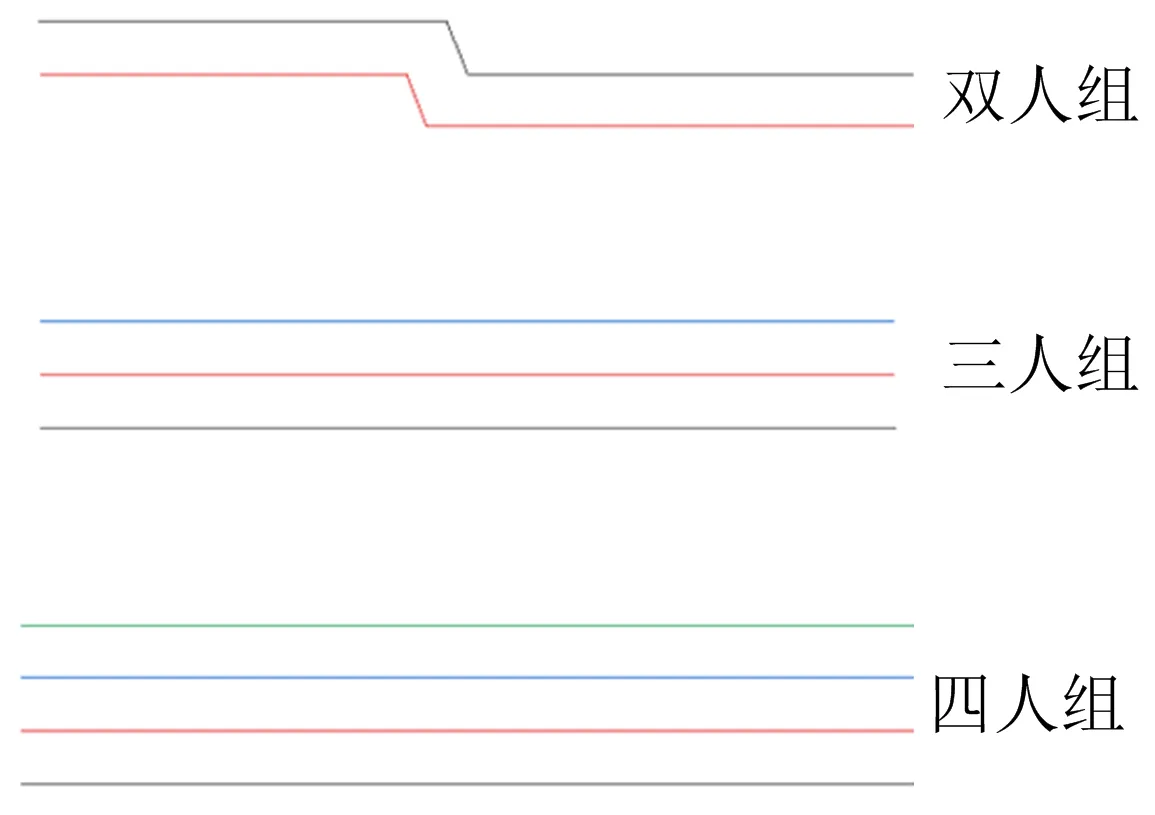
图12 无干扰情况下群组运动轨迹图

2.4 预测场参数分析

参考Suma等[23]的分析方法，本文将不往2方向(以从左往右行人为例，从右往左行人则为4方向)行走的时间步认为是时间损失，将该时间损失进行细化分类，图13为时间损失类别示意图，其中：

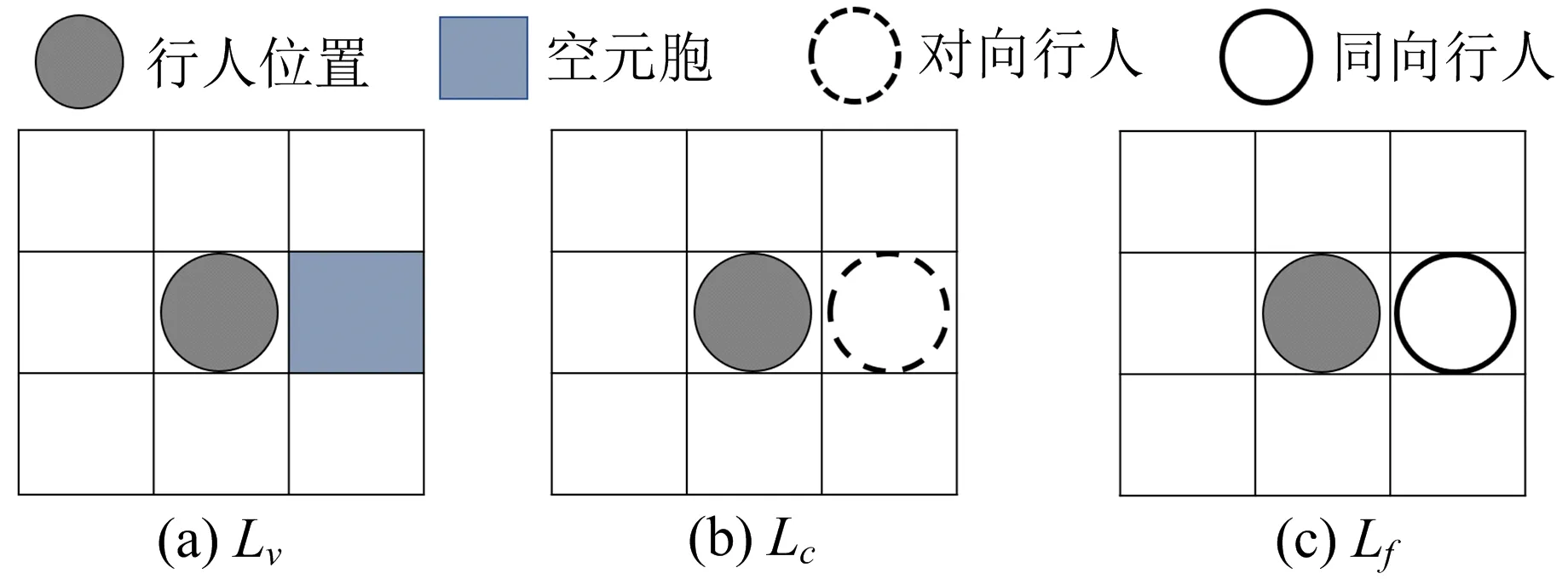
图13 时间损失类别示意图

(a)Lv为空元胞的时间损失，即2方向为空元胞却不往正前方行走的时间损失；

(b)Lc为反向行人的时间损失，即2方向被反向行人占据无法往正前方行走的时间损失；

(c)Lf为同向行人的时间损失，即2方向被同向行人占据无法往正前方行走的时间损失。

图14为在6 m×8 m的通道中模拟收集得到的时间损失情况。模拟场景为包含混合群组的双向行人流，两端各30人，平均分布有单人组、双人组、三人组、四人组。每一场景模拟1 000次。图14(a)中Lc随着ka的增大而降低，各规模群组均在ka取0.8前有大幅度的下降，而后下降幅度变缓，最终趋于稳定。从群组规模来看，Lc随着群组的增大逐渐减小。图14(b)中，从群组规模来看，Lf随规模的增大而增大，ka<2时不同规模群组的差异小于ka>2。图14(c)中，不同规模群组的Lv值基本趋于一致。Lv、Lf、T的曲线波动轨迹几乎相同。ka增大时，行人提前改变方向避让对向行人的概率增大导致Lv增大。避让对向行人时改变方向等行为，影响到同向行人的正常通行，与同向行人冲突增多导致Lf增大。同向行人正常通行受到了干扰，会增加通过的时间，最终导致了总的通过时间T增加。Lv、Lf、T在ka取值大于5时的震荡现象是由于预测场所产生的避让意识过强，在冲突区域存在疏散失败现象导致的。

图14 ka变化时对时间损失及总通过时间的影响

2.5 构型分析

我们对比使用预判距离阈值及不使用预判距离阈值时不同规模群组的构型差异。两个场景的预测场敏感性参数ka均为0.8。使用以上参数模拟在6 m×16 m通道中的双向行人运动，初始化时通道两端各10人，即单人组、双人组、三人组、四人组每种类型群组各一组，共重复进行5 000次实验。将空间等分为0.05 m×0.05 m的小区域，记录所有群组成员每一时间步以群组重心作为坐标原点的相对位置，每次实验的平均相对位置作为群组成员的占据位置。以此方法统计出5 000次重复实验中以群组重心为坐标的周围区域被占据的次数，如图15所示。

(a、c、e中不考虑预判距离阈值，b、d、f中考虑预判距离阈值)

图15(a)、图15(c)、图15(e)为不考虑预判距离阈值时绘制的相对位置占有次数图，图15(b)、图15(d)、图15(f)为考虑预判距离阈值时绘制的相对位置占有次数图。由图15可见，不同规模群组均为并肩行走出现的次数最高，两种场景下均能模拟出群组内部成员之间维持较近距离的运动特征，考虑预判距离阈值可以减少同组成员之间的冲突。图15(a)中大量四人组成员在重心半径1元胞的范围内凝聚，群组成员间冲突较为严重，而图15(b)中当考虑预判距离阈值时，四人组成员在重心半径1元胞的范围内凝聚较为分散，即成员间的冲突较少，因此构型较为稳定。图15(c)、图15(d)中三人组的构型主要为肩并肩行走，“∧”、“∨”的构型也可被观察到。对于双人组来说均能较好得维持肩并肩行走。

2.6 群组对行人流速度的影响

我们对比分析行人流中含有一类行人及含有多类行人的速度差异。图16中的单纯群组指通道中仅存在一类群组。图17中的混合群组指通道中同时存在单人组、双人组、三人组、四人组，群组组数比例为1∶1∶1∶1。在长为24 m的循环通道中进行模拟，每一种密度下的实验均重复20次，每次运行5 000时间步。模拟中的期望速度为1 m/s，即每一个时间步为0.4 s，图16、图17中的速度为往正前方即2方向行走(以从左往右行人为例，从右往左行人则为4方向)的距离除以时间。

图16 不同密度下单纯群组的速度

图17 不同密度下混合群组的速度

从图16、图17中看出，两种场景下的速度均随着密度的增加逐渐减低，最终到达阻塞状态速度为0。单纯群组中双人组、三人组、四人组与单人组平均速度差值均大于0.510 m/s，而混合群组中的平均速度差值均在0.08 m/s以下，单纯群组的速度差异性大于混合群组，混合群组各密度下的速度差异性较微小。密度在1.70人/m2之前，两种场景下不同规模群组的速度均为单人组>双人组>三人组>四人组。密度在1.70人/m2之后，单纯群组场景中速度最快交替出现在三人组与四人组之间，单人组的速度小于双人组。这一现象可能是由于，低密度时群组为维持构型需要花费一定的时间，群组规模越大花费时间越多，则速度越慢。而在高密度情况下，没有足够的行走空间，行走速度缓慢，群组之间自成的小群体抱团行走自动分层，减小了行人之间的摩擦力，因此大群组的速度反而比小群组快，即群组的存在能够提高通过效率，这与Zhang等[6]的结果相识。

3 总结

本文在场域模型中引入了群组场及预测场，在含有群组的双向流中进行模拟。结果表明增加预测场能够模拟群组行人提前避让的行为，预测场敏感性参数取值过大会影响通过效率。增加预测距离阈值与未考虑预测距离阈值相比可以减小群组成员之间的冲突，使行走构型稳定。在含有群组的通道中，行人的速度随着密度增加而减小。在仅考虑一种类型群组时，在密度较低情况下，群组规模越小速度越快，而在高密度情况下，最快速度在三人组、四人组之间交替出现，即高密度场景中大群组的存在能够提高通过速度。混合群组场景与单纯群组场景的速度有一定的差异性，群组存在对通过效率的影响值得深入研究。