超大型浮体运动与波浪载荷的水弹性响应分析

李志乐　李平　陈超核

摘    要：本文建立了桁架式超大型浮体（VLFS）构型方案，并采用迁移矩阵法进行模态分析;然后，基于三维水弹性理论方法，对该VLFS进行了运动与载荷响应计算，分析了不同海况和浪向角对浮体运动与载荷响应的影响;最后，将水弹性计算结果与基于刚体假设的载荷计算结果进行了对比，以分析弹性效应对浮体波浪载荷的影响。

关键词：三维水弹性;超大型浮体;浮体运动;波浪载荷

中图分类号：U661.35                              文献标识码：A

Abstract：  In this paper， the configuration scheme of truss type very large floating structure （VLFS） is established， and the modal analysis is carried out by using the transfer matrix method. Then， based on the three-dimensional hydroelastic theory， the motion and load response of VLFS are calculated to analyze the influence of movement and load response in different sea conditions and wave directions on the floating structure. Finally， the hydroelastic calculation results are compared with the load calculation results based on rigid body hypothesis to analyze the influence of elastic effect on wave load of the floating structure.

Key words： Three-dimensional hydroelasticity; VLFS; Movement of floating structure; Wave load

1     引言

随着全球城市的迅速扩张，沿海城市对可开发土地的需求量显著增加，国际船舶与海洋工程领域出现了新的研究热点——超大型浮体（简称VLFS）。超大型浮体的总长度可达千米、排水量可达百万吨级、造价可达百亿，主要用于漂浮的机场、港口、浮动船坞、桥梁、太阳能发电厂和浮动城市等。

因超大型浮体总体跨度较大，弹性效应不可忽略，故应将其视为弹性体。初期对于VLFS结构载荷响应的研究，是通过二维水弹性理论来分析的。二维水弹性理论由Bishop，C.V等[1]（1977）提出，该理论在对弹性船体进行对称响应分析时适用;Wu，Y.S等[2]（1985）提出了广义流固耦合的边界条件，奠定了三维水弹性理论的基础;随后，许多学者开展了相关理论研究和试验验证[3-9]。

本文针对超大型浮体建立了有限元模型。首先对其进行了振动模态分析;然后基于三维频域水弹性理论，计算了该浮体在多种不同浪向角下的水动力系数、运动响应和剖面载荷，对不同浪向角下浮体的运动与载荷响应特性进行研究;最后对比了基于水弹性理论的計算结果与将浮体视为刚体的计算结果。

2    三维线性水弹性理论

三维水弹性理论的波激振动方程如下：

3    浮体参数及模态分析

3.1   浮体建模参数

本文引用文献[10]中的一种超大跨度的桁架式浮动平台，用MSC.Patran建立了具有圆柱状浮筒、上层甲板及联接杆的超大型浮体有限元模型，如图1所示。浮体的纵向压力与拉力主要由联接杆承担，而垂向弯曲和纵向扭转强度主要由浮筒结构承担;浮体模型共3 225个单元，其中Shell单元2 704个、Beam单元521个。Shell单元用作浮筒各面面板的模拟，Beam单元用作联接杆、骨材的模拟;浮体所使用材料为普通钢材，弹性模量E=206GPa、泊松比μ=0.3;浮筒结构直径为4 m、壁厚30 mm、相邻浮筒间的轴心距离为15 m，联接杆直径为1 m、壁厚15 mm。浮体主要参数如表1所列。

由于后续需要对浮体进行水动力系数、运动响应、剖面载荷计算，因此需要建立分段质量模型，其中计算剖面数为21个，将浮体划分为20个分段。图2是载荷计算剖面示意图。

3.2   模态分析

本文基于迁移矩阵法对VLFS进行垂向弯曲模态的计算。迁移矩阵法是将复杂弹性体分解成相对简单的弹性部件的数值解法。具体操作：将弹性体分成若干个部件，以各个部件的结合点为考察对象，将结合点的状态矢量列出，然后利用弹性体振动时各部件间的传递关系，列出迁移矩阵并利用弹性体的边界条件，求得振动系统的数值解。

浮体的垂向位移、转角、垂向剪切力、垂向弯矩的固有振型曲线，如图3所示。图中Pr=7，Pr=8、Pr=9，分别代表二、三、四节点垂向振动模态（即一、二、三阶垂向振动模态）。浮体弯曲模态的固有频率为：一阶4.94 rad/s，二阶12.67 rad/s，三阶19.89 rad/s。

4     计算结果分析

基于上述理论，运用三维线性水弹性程序计算浮体在不同浪向角下的水动力系数、运动响应和剖面载荷。浮体处于自由飘浮且零航速的状态，只受到流体压力，忽略系泊力、推进力、风和流等作用;波浪类型为规则波;水深为无限深。

4.1   水动力系数

图4为浮体无航速状态下部分运动的附加质量和阻尼系数，包括垂荡运动（对应下标为33）和纵摇运动（对应下标为55）。其结果显示：

（1）附加质量：垂荡的附加质量在低频段内就出现最大值;纵摇则在低频段内随着频率的增大而增大，在0.4 rad/s处达到峰值;二者皆在出现峰值后出现骤减，最后趋于平稳，其中纵摇的附加质量幅值远大于垂荡;

（2）阻尼系数：垂荡、纵摇在低频段时的阻尼系数较小，但随后增长很快，两者皆在0.7～0.8 rad/s范围内达到峰值，之后迅速减少，其中纵摇的阻尼系数幅值远大于垂荡。

4.2   运动响应

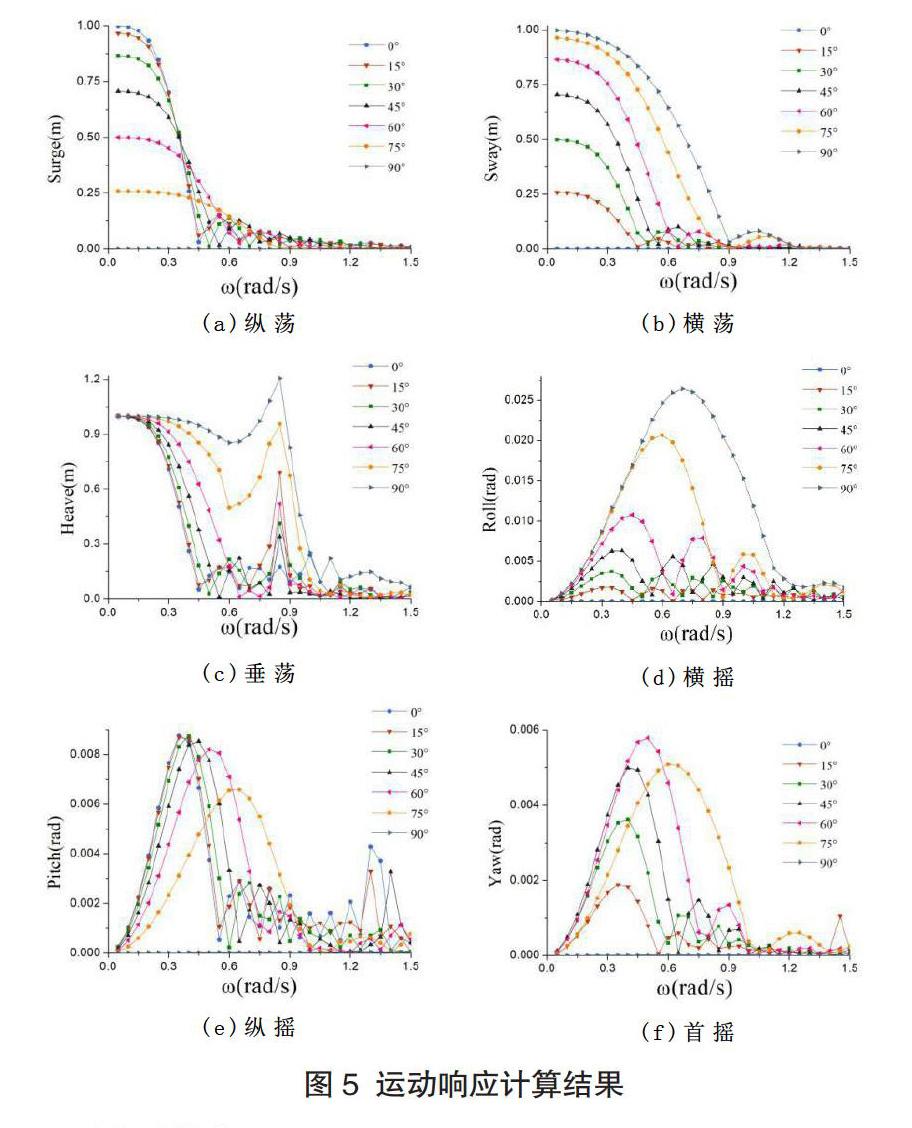
图5为浮体在波浪频率为0.05～1.5 rad/s、间隔为0.05rad/s的运动响应结果，其中选取了0～90°、间隔为15°的七个浪向角度。其结果显示：

（1）总体趋势：纵荡、横荡响应幅值皆在低频段达到峰值，然后迅速下降并趋向平稳;垂荡运动由较高值下降后回升至峰值，然后降至较低值;而横摇、纵摇、首摇运动响应幅值，则在低频段由零持续增长至峰值后降至较低值，其中纵摇运动响应幅值在高频段发生了不规则波动;

（2）总体峰值：纵荡、横荡与垂荡运动响应峰值差距较小，而横摇运动响应峰值比纵摇、首摇大得多;纵荡、横荡响应峰值皆出现在低频段，垂荡响应峰值在0.85 rad/s附近达到峰值，横摇在0.7 rad/s附近达到峰值，纵摇、首摇则分别在0.35 rad/s、0.5 rad/s附近出现最大值;

（3）不同浪向角的响应：纵荡、纵摇的最大响应幅值发生在迎浪（0°）;横荡、垂荡和横摇的最大响应幅值出现在横浪（90°）;首摇则在斜浪角（60°）出现最大响应幅值。

4.3   剖面载荷

图6为浮体在迎浪（0°）角和斜浪（45°）角下的剖面载荷随波浪波长与浮体长度比（λ/L）变化的曲线。其中选取了浮体1/4剖面处和1/2剖面处作分析，并与把浮体视为刚体的计算结果作了对比。其结果显示：

（1）对于迎浪（0°）：当波长相对浮体长度较小时，浮体结构载荷均较小;当波长接近浮体长度时，浮体整体弹性变形较明显;当波长大于浮体长度时，浮体剖面载荷随波长的增大逐渐减少;1/4剖面处和1/2剖面处的垂向剪切力分别在波长船长比为0.9和0.6时出现峰值，而垂向弯矩则都在波长船长比为0.9时达到峰值。可见在迎浪角下，浮体中部所受最大弯矩对应的波浪波长比较接近浮体总长度。

（2）对于斜浪（45°）：浮体载荷分布规律同迎浪（0°）状态，但总体载荷值比迎浪（0°）时小;1/4剖面处和1/2剖面处的垂向剪切力分别在波长船长比为0.6和0.5附近出现峰值，而垂向弯矩则都在波长船长比为0.6时达到峰值;

（3）由两种理论假设的计算结果对比可以看出，水弹性计算结果与基于刚体假设的计算结果趋势一致，水弹性理论的计算值相对较小，这充分说明对于本文这种桁架式超大型浮体，弹性效应是较为明显的。因此，在此类浮体的波浪载荷计算过程中，应充分考虑弹性效应。

5     结论

本文针对超大型浮体建立了有限元模型，并对其进行了振动模态分析，然后用三维水弹性计算程序进行了计算分析。结果显示：

（1）水动力系数方面：纵摇的附加质量、阻尼系数幅值都远大于垂荡;二者随频率变化的趋势相似，垂荡附加质量幅值在低频段与纵摇有微小差别;

（2）运动响应方面：纵荡、横荡与垂荡的响应峰值差距较小，而横摇的响应峰值比纵摇、首摇大得多;横浪运动响应总体较大;

（3）剖面载荷方面：浮体在迎浪角与斜浪角下的载荷分布规律相似。在迎浪角（0°）下，浮体中部受到的最大弯矩对应波浪波长比较接近浮体总长度，总体载荷值比斜浪時大;与此同时，基于水弹性理论与基于刚体假设的计算结果对比显示，本文的桁架式超大型浮体的水弹性效应明显，应予以考虑。

参考文献

[1]Betts， C.V.， Bishop， R.E.D and Prices， W.G. The symmetric generalized fluid forces applied to a ship in a seaway[J]. Trans RINA， 1977，119：265-278.

[2]Wu， Y.S. Hydroelasticity of floating bodies[D]. UK： Brunel University，1984.

[3]Price， W.G. and Wu， Y.S. Hydroelasticity of marine structure[J]. Theoretical and Applied Mechanics，1985：311-337.

[4]李辉.船舶波浪载荷的三维水弹性分析方法研究[D].哈尔滨：哈尔滨工程大学，2009.

[5]崔维成.超大型海洋浮式结构物动力特性研究综述[J].船舶力学，2001，5（1）：73-81.

[6]吕海宁，杨建民，姚美旺.箱式超大型浮体在非均匀海洋环境下的水弹性试验[J].海洋工程，2004，22（1）：1-6.

[7]Joo-Seong Yoon， Seong-Pil Cho， Phill-Seung Lee， et al. Hydroelastic analysis of floating plates with multiple hinge connections in regular waves[J]. Selected Papers of Chinese Society of Naval Architecture and Marine Engineering， 2014，36：65-87.

[8]杨鹏，顾学康.超大型浮体模块水弹性响应和结构强度分析[J].船舶力学，2015，19（05）：553-565.

[9]刘磊磊.桁架式超大型浮体波浪载荷计算方法研究[D].哈尔滨工程大学，2015.

[10]袁晓纪.一种超大型桁架式海上浮动平台[P].中国：CN1657360，2005-08-24.