受限玻尔兹曼机结合聚类的特异点挖掘方法

董鑫 夏文瀚 倪健 黄强 聂斌

摘 要：为了减少高维数据“维数灾难”对聚类效果的影响，将高斯受限玻尔兹曼机与DBSCAN算法相结合。首先利用高斯受限玻尔兹曼机对训练数据进行降维，然后采用DBSCAN算法识别降维后的数据特异点，最后利用UCI数据集中的数据进行实验验证，并开发了相应演示系统。实验选取UCI数据集中的3组数据进行验证，结果发现，该方法准确率分别为0.778、0.714、0.900，分别比DBSCAN算法提高了0.19、0.514、0.186，效果优于DBSCAN算法。因此高斯受限玻尔兹曼机与DBSCAN算法结合不仅能提高识别结果准确度，而且能提升识别效率。

关键词：受限玻尔兹曼机;聚类算法;特异点

DOI：10. 11907/rjdk. 191551 开放科学（资源服务）标识码（OSID）：

中图分类号：TP391文献标识码：A 文章编号：1672-7800（2020）002-0136-04

英标：Mining Specific Points Based on Restricted Boltzmann Machine and Clustering Method

英作：DONG Xin， XIA Wen-han， NI Jian， HUANG Qiang， NIE Bin

英单：（College of Computer Science， Jiangxi University of Traditional Chinese Medicine， Nanchang 330004，China）

Abstract： In order to combine the restricted Gaussian Boltzmann machine with the DBSCAN algorithm， singular point recognition is realized. The restricted Gaussian Boltzmann machine is combined with the DBSCAN algorithm. Firstly， the restricted Gaussian Boltzmann machine is used to reduce the dimension of the training data， then the dimension-reduced data is identified by the DBSCAN algorithm for singular point identification. Finally， the data in the UCI data set is used for experimental verification， and the demonstration system is developed accordingly. The experiment selected three sets of data in the UCI data set. The accuracy of the method was 0.778， 0.714， and 0.900， respectively， which were 0.19， 0.514， and 0.186 higher than the DBSCAN algorithm. Experimental results show that the proposed method outperforms the DBSCAN algorithm. The combination of the restricted Gaussian Boltzmann machine and the DBSCAN algorithm not only improves the accuracy of the recognition results， but also improves the recognition efficiency.

Key Words： restricted Boltzmann machine; clustering algorithm; outlier point

0 引言

聚類是一种无监督学习手段，其目的是将相似的数据点划分到同一类中，将不相似的数据点划分到不同的类中或归于噪声类。然而在实际应用领域，数据变得越来越复杂、维度越来越高，难以实现正确的分类。针对高维数据“维数灾难”问题，本文探求高斯受限玻尔兹曼机与DBSCAN算法结合的方法，着力于减少高维数据“维数灾难”对聚类效果的影响。

1943 年，心理学家McCulloch和数学家 Pitts等[1]提出了神经元数学模型，简称为MP模型，1949 年Hebb[2]首次提出使用神经网络进行学习的设想，1958年Rosenblatt[3]提出感知器模型及配套的学习训练方法。之后由于感知器存在种种缺陷，神经网络应用陷入低潮，但随着神经网络新模型和新算法相继出现，如Hopfield 神经网络[4]、玻尔兹曼机[5]等，神经网络再次引起研究人员关注。

2006 年，Geoffrey Hinton[6]提出深度信念网络（Deep Belief Nets，DBN）模型，该模型既可以对数据的概率分布进行建模，也可以对数据作类别分析[6-7]。DBN 也可称为生成模型，经过有效的模型训练，以最大的概率生成训练数据。从模型结构图来说，深度信念网络由受限玻尔兹曼机（Restricted Boltzmann Machines，RBM）堆叠而成，RBM 逐层探测数据内部规律，识别数据独特特征，判别数据真实类别[8]。目前，RBM因自身强大的特征提取能力及作为深度信念网络的基本构成模块，引起了机器学习界密切关注，在众多领域得到了广泛应用[9]。

在涉及向量计算的实际应用中，随着维数增加，常出现计算量呈指数倍增长的“维数灾难”，学者们对该问题从不同角度进行了研究。叶福兰[10]提出基于核函数的高维离散数据聚类算法;针对高维空间中数据分布的稀疏性和空间特性，李慧敏等[11]设计了一种基于信息熵的相似性度量方法，取得了较好的聚类效果;为解决传统DBSCAN方法对高维数据不适用的问题，姜洪权等[12]提出一种基于KPCA与DBSCAN的高维非线性特征数据聚类分析技术。

基于RBM快速学习算法聚类是无监督的，适合不含类标记的大规模数据。RBM 算法已成功应用于分类、回归、降维、特异点识别等不同的机器学习问题 [13-16]。为了构建RBM 算法与聚类算法结合识别特异点的方法，研究如何减少高维数据“维数灾难”对聚类效果的影响，本文提出将高斯受限玻尔兹曼机与DBSCAN聚类算法结合的方法。首先采用高斯受限玻尔兹曼机降维，使维数对聚类效果的影响显著减小，再结合DBSCAN聚类，检测和发现特异点。

1 RBM模型与DBSCAN算法介绍

1.1 RBM模型介绍

受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）是深度概率模型中最常见的组件之一。RBM本身不是一个深层模型，相反，它有一层潜变量，可表示学习输入[17]。

RBM是一类具有两层结构、对称连接且无自反馈的随机神经网络模型，层间全连接，层内无连接，标准的RBM是基于能量的模型[18]。二值RBM虽在图像领域已取得极好的成果，也是应用最广泛的 RBM 模型，但在实际应用中还存在不足。

高斯受限玻尔兹曼机与传统二值受限玻尔兹曼机不同，它是实值数据上的受限玻尔兹曼机。在高斯 RBM 模型中可见层的变量服从高斯分布，隐层变量与二值 RBM 相同，服从二值分布。在给定隐层变量的情况下，可见层变量的分布是高斯专家乘积模型，每一个专家服从高斯分布，相应地，在给定可见层变量的情况下，隐层变量也是二值专家乘积模型[19]。

1.2 DBSCAN算法

DBSCAN算法[20]是经典的基于密度的聚类算法，基本原理是通过寻找数据点密度相连的最大集合寻找聚类最终结果。与划分及层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声空间数据库中发现任意形状的聚类[21]。

其优点主要体现于：①聚类速度快并且能够处理任意形状和大小的簇[22]，能够发现数据集中的噪声，多次运行结果相对稳定;②不需要输入待划分的聚类个数;③算法中聚类簇的形状没有偏倚[23]。同时缺点包括：①参数较难确定[24]，当簇的密度不均匀（变化较大）时很难发现所有的簇[25-26];②对于高维数据，由于传统欧几里得距离不能很好地处理高维数据，无法很好地定义距离。

2 RBM模型与DBSCAN算法融合

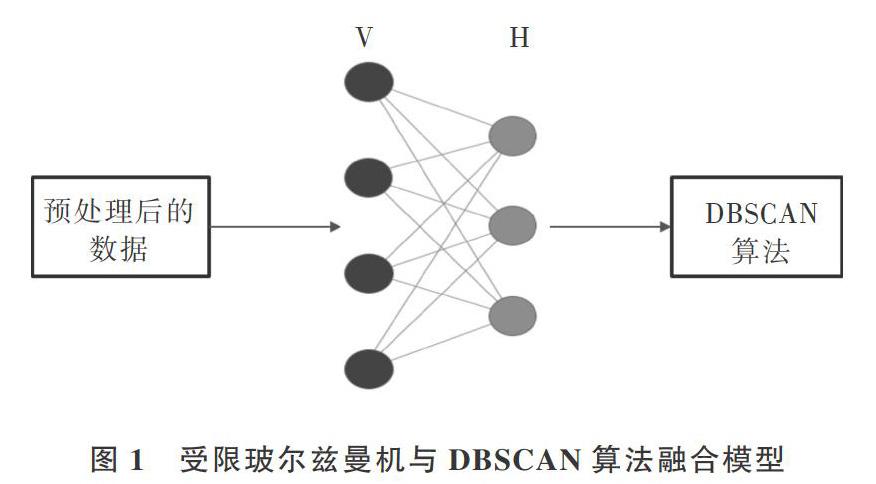
本文提出的基于受限玻尔兹曼机与聚类方法结合挖掘特异点的模型如图1所示，该模型由两部分组成，即顶层高斯受限玻尔兹曼机和底层DBSCAN。高斯受限玻尔兹曼机由两层结构组成，一层可见层，一层隐藏层。首先将原始数据集进行归一化处理，然后再将归一化后的训练数据集输入高斯受限波尔兹曼机的可见层，得到经过高斯受限玻尔兹曼机训练后的数据集，最后将经过训练的数据集输入DBSCAN中挖掘特异点。

与传统DBSCAN算法相比，经高斯受限玻尔兹曼机调整参数后，训练后的数据集更适合DBSCAN算法进行特异点分析，从而可获得比传统DBSCAN算法更好的效果。

在高斯受限玻尔兹曼机中，参数设置非常重要，参数的选择对最后结果会造成很大影响。它并不是简单地对数据进行降维，还要保证经过训练后的数据集适合DBSCAN算法进行特异点挖掘工作。设置的参数包括隐藏层层数、训练周期和每周期训练数据大小。對于隐藏层层数设置，本文将未经训练的数据集维数除以2，之后以该数为基准上下调整，直至得到满意的结果，确定最后参数。后两个参数的设置比较简单，经过多次实验探索，发现训练周期设置在500～1 000内训练，每周期训练数据大小略高于训练数据集数据大小时，训练速度快、效果稳定。

在DBSCAN算法中距离半径[ε]和点数阈值MinPts也需要设置。一般可以用观察第k个最近邻距离（k距离）的方法确定这两个参数。对于属于某个簇的点，如果k不大于簇的样本个数，则k距离很小。然而，对于不在簇中的点（噪声），k距离将相对扩大。因此，对于任意一个正整数k，计算所有数据点k的距离，然后以递增顺序将它们排序，绘制排序后的k距离值，将看到k距离的急剧变化转折点，该点对应的距离一般对应于合适的[ε]值。如果此时选取k值为MinPts，则k距离小于[ε]的点将被标记为核心对象，其它点将被标记为边界对象或噪声。利用k距离方法得到的[ε]值取决于k，但是并不随着k的改变而剧烈变化。如果k值很小，则少量噪声点将被标记为簇;如果k值太大，则数量小于k的簇可能被标记为噪声。最初DBSCAN算法选取k=4，然后根据实验结果再进行调参，一般选3或5即可确定是否需要更改参数。

3 实验验证与分析

实验中将改进后的算法与传统DBSCAN算法作比较，从检测召回率、精确度和F值上对比算法性能。本实验采用的数据集全部来自UCI机器数据库。共选取3个数据集进行训练和测试，分别为：威斯康星州乳腺癌（诊断）数据集（Breast Cancer Wisconsin （Diagnostic） Data Set，BCW）、葡萄酒数据集（Wine Data Set，Wine）、Parkinson数据集（Parkinson Data Set，PK），其维数分别为30、13、22。本实验采用多个维度的数据集进行测试，从而更好地评估改进后的算法效果。

使用整个数据集，在DBSCAN算法的数据中加入10个特异点;对于用于算法改进后的数据，分别将每个数据集的70%作为训练数据集，30%作为测试数据集，然后在训练数据集中加入其数据总量5%的特异点，测试数据集中加入其数据总量20%的特异点，特异点所有维度均匀分布在U（0，1）上随机生成。实验前将数据集进行预处理，将数据集统一归一化至[0，1]。数据类别标签分为两种情况，一种是大于1的整数，代表正常类，另一种是-1，代表特异点。

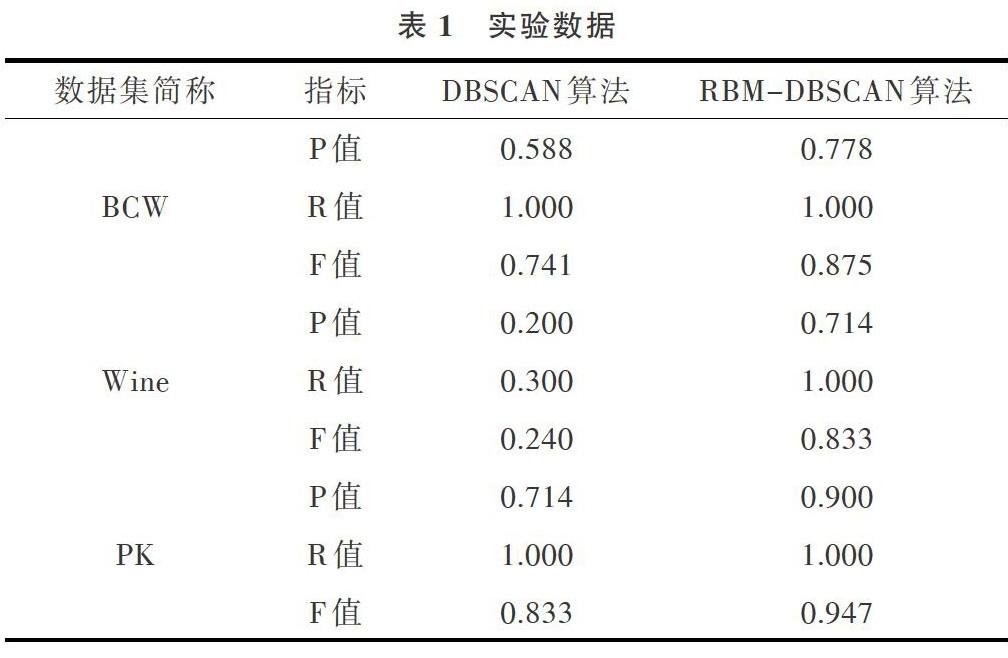
然后利用已处理的数据进行实验，实验用改进算法和传统DBSCAN算法进行对比。通过对以上3个数据集进行特异点挖掘分析，实验结果如表1所示（精确度（P值）、召回率（R值）、F值均保留三位有效数字）。

通过表1可看出，改进后的算法（RBM-DBSCAN）比改进前的算法（DBSCAN）在P值、R值、F值上均有更好表现。

4 RBM与聚类算法融合挖掘特异点系统实现

本系统主要用于实现RBM与聚类算法融合过程及融合算法的可视化结果呈现。

4.1 系统总界面实现

系统总界面包括项目简介、原始DBSCAN算法实现数据聚类、融合算法实现数据聚类、作者信息等内容，为体现数据维数不固定性及算法本质，融合算法实现聚类部分还包括单层网络聚类与双层网络聚类，其中单层网络供低维数据使用，双层网络供高维数据使用。

4.2 调整参数实现

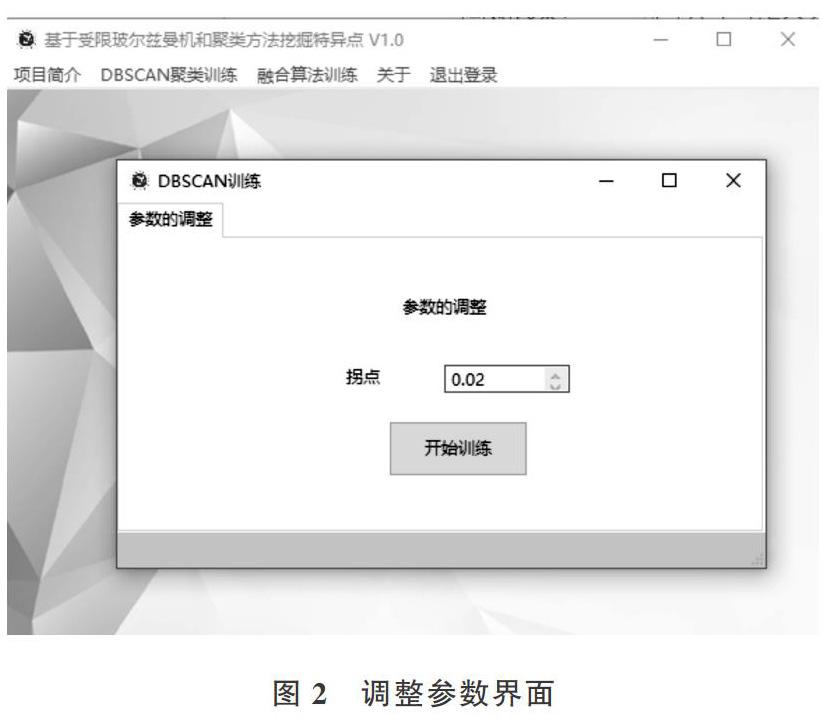
本系统中最关键的是参数调整，参数调整的好坏直接影响算法结果。由于参数的不固定性，故本系统为使用者提供输入框，让用户在框中输入参数，然后传到算法中并调用算法实现数据聚类。以原始DBSCAN算法对数据聚类，进行参数调整的界面为例进行展现，如图2所示。

在参数传入界面内，点击“开始训练”按钮进行算法调用与运行，之后将展示算法运行结果，如图3所示。

4.3 其它功能实现

除核心功能外，系统还有一些辅助功能，如展示項目简介、作者信息、退出系统等。本部分阐述的界面脚本已将该算法功能基本实现，达到了算法功能可视化的目的。

5 结语

本文初步研究了受限玻尔兹曼机结合聚类挖掘特异点的方法，加深了对受限玻尔兹曼机在特异点挖掘应用上的认识。本文首先进行高斯受限玻尔兹曼机降维，使维数对聚类效果的影响显著降低，再结合DBSCAN聚类，检测和发现特异点，并用实验验证该方法有效，最后利用wxPython实现算法可视化和算法所需功能。未来研究将进一步加强高维数据降维，探索更有效的深度融合方法。

参考文献：

[1] MCCULLOCH W S， PITTS W. A logical calculus of the ideas immanent in nervous activity[J].  Bulletin of Mathematical Biology， 1990， 52（1-2）：99-115.

[2] HEBB D O. In the organization of behavior， a neuropsychological theory[M].  New York： John Wiley， 1949.

[3] ROSENBLATT F. The perceptron： a probabilistic model for information storage and organization in the brain[M]. Cambirdge：MIT Press， 1988.

[4] HOPFIELD J J. Neural networks and physical systems with emergent collective computational abilities[J]. Proceedings of the National Academy of Sciences of the United States of America， 1982， 79（8）：2554-2558.

[5] ACKLEY D H， HINTON G E， SEJNOWSKI T J. A learning algorithm for Boltzmann  machines*[J]. Cognitive Science，1985，9（1）：147-169.

[6] Hinton G H，SEJNOWSKI T J，ACKLEY D H. Bolzmann machines：constraint satisfaction networks that learn[R]. Technical Report CMU-CS，1995：84-11.

[7] 刘建伟，黎海恩，周佳佳，等. 概率图模型的表示理论综述[J]. 电子学报，2016，44 （5）：1219-1226.

[8] 彭丽霞.  深度信念网络的模型选择问题研究[D]. 成都：西南交通大学，2018.

[9] 罗剑江. 受限玻尔兹曼机的改进及其应用[D]. 广州：广东工业大学，2017.

[10] 叶福兰. 基于核函数的高维离散数据聚类算法研究与应用[J]. 长春工程学院学报：自然科学版，2018，19（3）：79-81.

[11] 李慧敏，李川. 高维数据聚类中相似性度量算法的改进[J]. 内蒙古统计，2018，（2）：21-25.

[12] 姜洪权，王岗，高建民， 等. 一种适用于高维非线性特征数据的聚类算法及应用[J]. 西安交通大学学报，2017，51（12）：49-55，90.

[13] 吴证，周越，杜春华，等. 组合主成分分析的受限波尔兹曼机神经网络的降维方法[J]. 上海交通大学学报，2008，42（4）：559-563.

[14] CHANDRA S，KUMAR S，JAWAHAR C V. Learning multiple non-linear sub-spaces using K-RBMs[C].  2013 IEEE Conference on Computer Vision and Pattern Recognition， 2778-2785.

[15] YUAN M L， TANG H J， LI H Z. Real-time keypoint recognition using restricted Boltzmann machine[J].  IEEE Transactions on Neural Networks and Learning Systems， 2014， 25（11）：2119-2126.

[16] CHEN Y L， LU L J， LI X B. Application of continuous restricted Boltzmann machine to identify multivariate geochemical anomaly [J]. Journal of Geochemical Exploration，2014，140：56-63.

[17] SMONLENSKY P. Information processing in dynamical systems：Foundations of harmony theory[J].  Parallel Distributed Processing，1986，1（6）：194-281.

[18] 刘建伟，刘媛，罗雄麟. 玻尔兹曼机研究进展[J]. 计算机研究与发展，2014，51（1）：1-16.

[19] 沈卉卉，李宏伟. 基于受限玻尔兹曼机的专家乘积系统的一种改进算法[J]. 电子与信息学报，2018，（9）：2173-2181.

[20] 刘维. 数据挖掘中聚类算法综述[J]. 江苏商论，2018，（7）：120-125.

[21] 冯振华，钱雪忠，赵娜娜.  Greedy DBSCAN：一种针对多密度聚类的DBSCAN改进算法[J]. 计算机应用研究，2016，（9）：2693-2696+2700.

[22] 庄夏. 基于DBSCAN和Kmeans的用户地理位置聚类算法研究[J]. 数字化用户，2018，24（1）：34-35，131.

[23] 宋董飞，徐华. DBSCAN算法研究及并行化实现[J]. 计算机工程与应用，2018，54（24）：52-56，122.

[24] 周红芳，王鹏.  DBSCAN算法中参数自适应确定方法的研究[J].  西安理工大学学报，2012，（3）：289-292.

[25] 李雙庆，慕升弟. 一种改进的DBSCAN算法及其应用[J].  计算机工程与应用，2014，（8）：72-76.

[26] 秦佳睿，徐蔚鸿，马红华，等. 自适应局部半径的DBSCAN聚类算法[J]. 小型微型计算机系统，2018，39（10）：2186-2190.

（责任编辑：江 艳）