基于非参数回归法的掺粉煤灰混凝土抗硫酸腐蚀能力预测
2020-05-25谢世华毛敏张彩虹郭会芳
谢世华 毛敏 张彩虹 郭会芳


摘 要:结合非参数回归技术分析,通过均匀试验设计方法得到的24组稀硫酸腐蚀掺粉煤灰混凝土试件试验数据,研究pH值、水胶比、水泥用量、粉煤灰用量、坍落度5个因素对混凝土腐蚀量的影响以及相应预测方法。结合试验数据,首先采用Pavlick建议的幂函数模型进行参数回归,获得各组试验的腐蚀系数k与时间指数n,然后在此基础上,采用ACE非参数回归技术分析腐蚀系数k与pH值、水胶比、水泥用量、粉煤灰用量、坍落度5个因素的关系,并建立腐蚀预测模型。结果表明:①幂函数模型能很好地反映腐蚀随时间的增长规律;②按浸泡过程中硫酸钙析出时间点不同,可将k、n值分布特征大致划分为3类,采用ACE回归分别建立不同类预测模型,能获得较好的预测结果。
关键词:硫酸腐蚀;掺粉煤灰混凝土;均匀试验;非参数回归
DOI:10. 11907/rjdk. 192156 开放科学(资源服务)标识码(OSID):
中图分类号:TP301文献标识码:A 文章编号:1672-7800(2020)002-0023-04
英标:Prediction Method for Corrosion Resistance of Fly-ash Concrete by Sulfuric Acid Based on Non-parametric Regression
英作:XIE Shi-hua,MAO Min,ZHANG Cai-hong,GUO Hui-fang
英单:(Faculty of Architectural Engineering,Kunming University of Science and Technology,Kunming 650500,China)
Abstract: The prediction method for corrosion resistance of fly-ash concrete (FAC) by sulfuric acid is investigated by non-parametric regression to study the effects of five influence factors, i.e. pH value, water-binder ratio, cement dosage, fly-ash dosage and slump. The experimental datum was obtained from 24 groups of uniform designed soaking tests of FAC specimens in dilute sulfuric acid. The power function model proposed by Pavlik was first applied to each group and obtained the corrosion coefficient k and time index n. Then, the corrosion prediction mode is established by analyzing the relationship between corrosion coefficient k and the five influence factors mentioned above with the non-parametric regression technique of ACE. Results show that: ① The power functions fit the experimental datum well; ② The distribution characteristics of k and n can be roughly divided into three categories according to the precipitation time of calcium sulfate during immersion. A better prediction can be obtained by using ACE non-parametric regression for different corrosion types.
Key Words: sulfuric acid corrosion; fly-ash concrete; uniform experiment; non-parametric regression
0 引言
如今,硫酸腐蝕造成的混凝土性能退化问题已越来越多地受到国内外学者关注[1-5]。如唐咸燕[6]通过试验研究发现,粉煤灰、矿渣微粉双掺对模拟酸雨条件下的水泥砂浆试件强度有一定改善作用;李北星[7]的试验研究表明,掺入20%粉煤灰的混凝土抗硫酸腐蚀性能最佳,并提出混凝土质量、强度变化与硫酸腐蚀时间的一元三次预测经验模型;Toeii[8]认为在普通混凝土中掺入一定量粉煤灰和硅灰可以有效提高砂浆对硫酸与硫酸盐的抗性;肖佳[9]试验研究表明,粉煤灰对水泥砂浆试件在模拟酸液条件下抗折强度没有改善作用。众多学者的研究结论并不统一,说明掺粉煤灰混凝土抗硫酸腐蚀的能力受粉煤灰用量[7]、腐蚀残留物[10-11]等多种因素影响,表现出较为复杂的规律,准确预测掺粉煤灰混凝土的抗硫酸侵蚀能力还存在一定困难。相比之下,结合大量试验结果,以非参数回归方法建立的预测模型精度高、适应能力强,可以获得复杂机制影响下试验数据的经验模型,因而在不同领域的试验研究中得到了广泛关注。如高宇等[12]基于非参数回归方法建立青霉素发酵过程软测量模型;华祖林[13]通过非参数回归方法对太湖总磷压力—响应模型进行改进;Alani[14]创建一种进化多项式回归技术(EPR)用于建立硫酸腐蚀混凝土预测经验模型,且其精度高于利用人工神经网络技术建立的回归模型;闵红光[15]在研究硫酸侵蚀混凝土时,验证了将均匀试验与非参数回归法相结合应用于试验研究的可行性及高效性。
为了绕开硫酸腐蚀混凝土的复杂规律,本文直接使用统计学软件S-PLUS提供的ACE(Alternating Conditional Expectations)非参数回归方法建立掺粉煤灰混凝土受硫酸腐蚀的预测经验模型。ACE非参数回归方法早在Hasofer[16]的研究中即得到了应用,但其主要应用于金融统计领域,在混凝土耐久性领域的应用非常少。本文通过分析24组采用均匀试验设计方法获得的试验结果,以硫酸消耗量表示掺粉煤灰混凝土试件腐蚀程度,结合ACE非参数回归方法,得到与pH值、水胶比、水泥用量、粉煤灰用量、坍落度5个因素相关的腐蚀预测经验模型,且模型精度较高。
1 试验设计及结果
本文以浸泡液pH值、水胶比和粉煤灰用量为基本因素设计24组均匀试验,试验设计表及试件配合比见表1。浸泡液体积为10L,在浸泡过程中定期往浸泡液里滴定稀硫酸以保持浸泡液的pH值稳定,滴定液溶度为0.5mol/L。各组试验耗酸量随时间变化曲线如图1-图4所示,由于部分组的试验数据结果比较接近,为表达清晰,图中绘制的试验组数并不一样,试验基本情况详见文献[17]。
假设掺粉煤灰混凝土耗酸量也可采用类似于pavlik等[18]提出的中性化深度公式表示。
式中,M(t)为耗酸量(mL),t为浸泡时间(h),k为腐蚀系数,n为时间指数,各组试验拟合出的k、n值和浸泡结束时(浸泡总时间T=3 570h)的耗酸总量S(mL)见表2。表2中,C為混凝土水泥材料比例,F为混凝土粉煤灰材料比例,Z为坍落度,nE为不同pH值范围内各组试验n的平均值。浸泡过程中会有硫酸钙析出,考虑到硫酸钙在18℃的溶解度为0.255,浸泡箱溶液体积为10L,反应生成的硫酸钙开始析出时,0.5mol/L稀硫酸消耗量为296mL。设各组试验耗酸量达到296mL的时间为Td,试验过程中硫酸钙析出后时间占浸泡总时间的比例Rt计算公式如下:
由表2可知,Pavlik提出的腐蚀幂函数模型与试验数据有很高的拟合度,同时k与n根据硫酸消耗量的不同可明确划分为3个区间。结合表中Rt分布特点不难看出,3个区间划分与硫酸钙析出有关,对应3种腐蚀类型:第一种腐蚀类型几乎没有硫酸钙析出,以溶蚀为主;第二种腐蚀类型为过渡类型,溶蚀和硫酸钙析出所起的作用相当;第三种腐蚀类型前期即大量析出硫酸钙,试件一边溶蚀,一边生成硫酸钙堵塞混凝土孔隙。Israel[19]&Yuan[20]的研究认为硫酸侵蚀混凝土产生的硫酸钙会堵塞混凝土孔隙,截断硫酸侵蚀混凝土的反应通道,减缓侵蚀速度。结合表2各组试验硫酸钙析出时间以及图1-图4耗酸曲线斜率变化情况,正好也印证了Israel&Yuan的结论。
2 ACE非参数回归分析
S-PLUS是基于S语言的统计学软件,是世界上公认的三大统计软件之一。其提供多种数据统计方法,ACE(Alternating Conditional Expectations)非参数回归方法即是其提供的数据统计方法之一。ACE非参数回归方法具有很强的适用性与精确性,其基本思想就是不事先假定函数形式,而是寻找输入参数x1,x2,…,xm与函数y之间的变换关系φ1(x1),φ2(x2),…,φm(xm)和θ(y),使其满足如下映射关系:
式中,ε为反映拟合精度的拟合误差,从而可以确定函数y为:
如果能够确定φ1(x1),φ2(x2),…,φm(xm)和θ(y)的函数形式,即可确定函数y的形式。
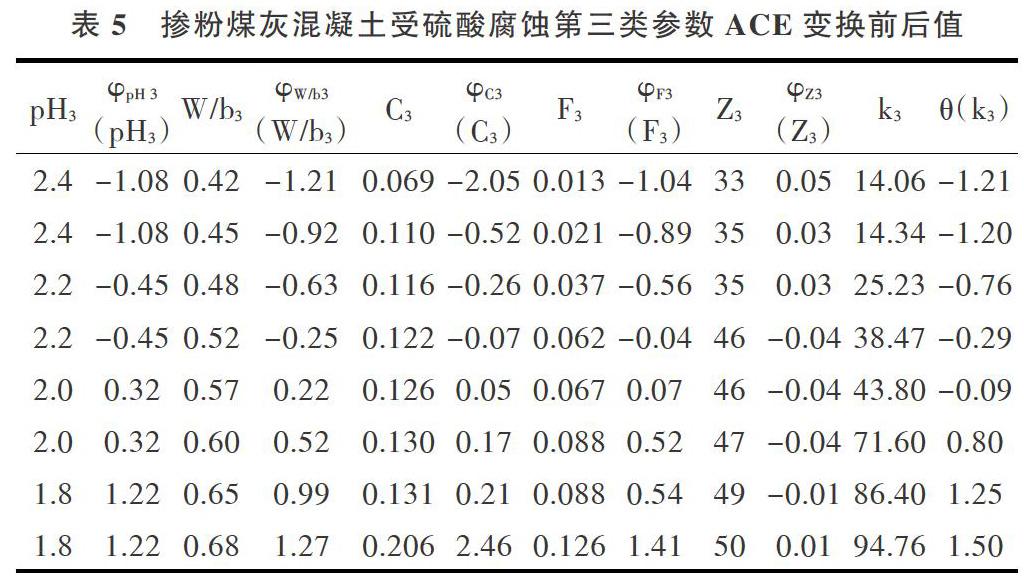
由于腐蚀系数k的变化范围较大,而每种类型的时间指数n又非常相近,因此只对腐蚀系数k进行ACE非参数回归分析,而对3种类型的时间指数n分别取其平均值nE。水胶比、水泥比例、粉煤灰比例、坍落度都是混凝土的重要参数,浸泡液pH值也是影响硫酸腐蚀混凝土的关键因素之一。在对腐蚀系数k进行ACE非参数回归分析时,应综合考虑以上5个影响因素。对于表2给出的输入输出数据,经过ACE变换后分别为φpH(pH)、φW/b(W/b)、φC(C)、φF(F)、φZ(Z)、θ(k)。3种类型的影响因素以及腐蚀系数k分别经过ACE变换前后的数值见表3-表5。为了更直观地显示各个因素经ACE变换前后的数学关系,对每个影响因素进行升序或降序处理,因此同一行并不是同一组数据。
影响因素经ACE变换后的数值取值区间长度越大,说明其对输出结果影响越大。由表3-表5可得到3种腐蚀类型各参数经ACE变换后的取值区间长度,如表6所示。
由表6可知,对于各种因素对硫酸腐蚀掺粉煤灰混凝土的影响大小而言,浸泡液pH值与粉煤灰比例始终都起着重要作用;水胶比与水泥比例的影响作用随硫酸钙析出量的增加而逐渐减弱;混凝土坍落度无论在哪种腐蚀类型情况下,所起的作用都相对较小,尤其是在硫酸钙析出逐渐占优的二、三两类,坍落度对应的映射函数范围比其它因素小一个量级,坍落度影响不占主导地位。
通过MATLAB软件分别拟合出各腐蚀类型pH~φpH(pH)、W/b~φW/b(W/b)、C~φC(C)、F~φF(F)、Z~φZ(Z)、k~θ(k)的函数关系,再联立式(3)和式(4)即可得到腐蚀系数k的回归函数为:
将式(5)-式(7)分别代入式(1)中,即可得到掺粉煤灰混凝土在硫酸环境下3种腐蚀类型的预测经验模型。将表2中3种腐蚀类型的5个原始参数分别代入其对应的回归函数式(5)-式(7)中,可得到回归值k。结合表2的试验值k,可得到腐蚀系数k回归值与试验值关系如图5所示,其中实线为45°线。
图5图像的点基本分布在45°线附近,k回归值与试验值吻合度非常高,说明3种类型的腐蚀系数k回归结果良好,回归模型精度较高。
3 结语
本文利用均匀试验设计的24组稀硫酸腐蚀掺粉煤灰混凝土试件试验数据,综合考虑pH值、水胶比、水泥比例、粉煤灰比例、坍落度5个影响因素,结合ACE非参数回归技术,得出以下结论:
(1) 幂函数模型能很好地反映掺粉煤灰混凝土在硫酸环境下腐蚀随时间的增长规律。
(2) 硫酸钙晶体会堵塞硫酸侵蚀混凝土的反应通道,因此受硫酸钙析出时间点及析出量影响,硫酸腐蚀掺粉煤灰混凝土可分为3类:第一种腐蚀类型几乎没有硫酸钙析出,以溶蚀为主;第二种腐蚀类型为过渡类型,溶蚀与硫酸钙析出所起作用相当;第三种腐蚀类型前期即大量析出硫酸钙,试件一边溶蚀,一边生成硫酸钙堵塞混凝土孔隙。
(3) 基于ACE非参数回归技术,综合考虑pH值、水胶比、水泥比例、粉煤灰比例、坍落度5个影响因素,分别建立硫酸侵蚀掺粉煤灰混凝土3种腐蚀类型的预测经验模型,且精度较高。
参考文献:
[1] 陈剑雄,吴建成,陈寒斌. 严重酸雨环境下建筑物的耐久性调查[J]. 混凝土, 2001(11):44-47.
[2] 宋志刚,杨圣元,刘铮,等. 昆明市区酸雨对混凝土结构侵蚀状况调查[J]. 混凝土,2007(11):23-27.
[3] MANSFELD F,LIN S, KIM K, et al. Pitting and surface modification of SIC/Al [J]. Corrosion Science,1987, 27(9):997-1000.
[4] 吴依平,王素芸. 酸沉降对建筑物的影响调查[J]. 上海环境科学, 1991(4):37-39.
[5] 韩静云,张小伟. 污水对初沉池混凝土不均衡损伤特性研究[J]. 土木工程学报,2005(7):45-49.
[6] 唐咸燕,肖佳,陈烽,等. 复合矿物掺合料对砂浆抗酸雨侵蚀性能的影响[J]. 粉煤灰综合利用, 2007(1):3-6.
[7] 李北星,周长泉,蔡老虎,等. 硫酸环境作用下粉煤灰混凝土性能劣化时变规律[J]. 材料科学与工程学报, 2014(6):809-815.
[8] TOEII K,KAWAMURA M. Effects of fly ash and silica fume on the resistance of mortar to sulfuric acid and sulfate acid [J]. Cement and Concrete Research,1994, 24(2):361-370.
[9] 肖佳,周士琼. 酸雨条件下低钙粉煤灰对水泥砂浆强度的影响[J]. 建筑材料学报,2005,8(4):440-445.
[10] 起洋砚,宋志刚, 战越. 稀硫酸侵蚀水泥砂浆的附面层效应研究[J]. 硅酸盐通报,2017,36(12):4296-4301.
[11] 宋志刚,李贤胜,谢世华, 等. 硫酸侵蚀混凝土的腐蚀产物附面层及其影响[J]. 建筑材料学报,2019,22(3):348-355,370.
[12] 高宇,王建林,于涛,等. 基于非参数回归的发酵过程软测量建模[J]. 北京化工大学学报(自然科学版),2016,43(5):74-78.
[13] 华祖林, 韩爱秋. 基于非参数回归改进的太湖总磷压力—响应模型[J]. 水资源保护,2019,35(1):20-24,46.
[14] ?ALANI A M, FARAMRZI A. An evolutionary approach to modelling concrete degradation due to sulphuric acid attack[J]. Applied Soft Computing, 2014, 24:985-993.
[15] 闵红光,宋志刚,张雪松. 均匀试验和非参数回归在硫酸侵蚀混凝土试验中的应用[J]. 河南科学, 2010,28(4):452-455.
[16] HASOFER A M, QU J. Response surface modelling of Monte Carlo fire data[J]. Fire Safety Journal,2002(37):772-784.
[17] 郭会芳. 掺粉煤灰、硅灰混凝土抗硫酸侵蚀性能的研究[D]. 昆明:昆明理工大学, 2012.
[18] PAVLIK V. Corrosion of hardened cement paste by acetic and nitric acids part I: calculation of corrosion depth [J]. Cement and Concrete Research, 1994, 24(3):551-562.
[19] ISRAEL D, MACPHEE D E, LACHOWSKI E E. Acid attack on pore-reduced cements[J]. Journal of Materials Science,1997, 32 (15):4109-4116.
[20] YUAN H F, PATRICK D, PATRICE C, et al. Degradation modeling of concrete submitted to sulfuric acid attack[J]. Cement and Concrete Research, 2013,53:267-277.
(責任编辑:黄 健)
