小波矩结合三维荧光光谱简单快速鉴别掺伪芝麻油
2020-05-25李瑞航吴希军崔耀耀
潘 钊,李瑞航,吴希军*,崔耀耀
1. 燕山大学河北省测试计量技术及仪器重点实验室,河北 秦皇岛 066004 2. 燕山大学信息科学与工程学院,河北 秦皇岛 066004
引 言
芝麻油又称香油,含有丰富的营养。因市场价格较高,掺假现象严重。违法商贩用菜籽油、大豆油、玉米油等廉价油勾兑芝麻香精降低成本进行销售,严重损害了消费者权益和市场健康[1],因此鉴别掺伪芝麻油具有重要应用意义。
掺假芝麻油与芝麻油气味、颜色等物理特性相近,无法肉眼区分。目前植物油的鉴别方法主要有红外光谱法[1-2]、拉曼光谱法[3]、色谱法[4]、荧光光谱法[5]及太赫兹法[6]等。荧光光谱法以其灵敏度高、操作简单、分析快速等优点在植物油鉴别领域具备一定的优势[5]。经典荧光分析方法结合主成分分析[7]、平行因子[8]、交替三线性分解[9]及偏最小二乘[10]等算法提取或分离荧光光谱的特征进行定性或定量分析取得了很好的效果。近年来,图像矩法被引用到三维光谱,被证明是定性或定量分析的强大工具[11-13]。但目前在三维光谱领域,有关图像矩法的相关报道较少,且缺乏较为全面的定性或定量的规律性分析。图像矩是从整个图像空间计算得到,反映目标的全局信息,包含丰富的光谱信息。通过找到样本分类的有效矩值,利用有效矩值即可将样本准确分类。矩值法计算量大,高阶矩严重敏感于噪声是矩值法在应用时的弊端[11]。
本文将小波矩引入三维荧光光谱的定性分析。将三维荧光光谱视为灰度图,利用小波矩提取光谱形状的几何信息。利用多尺度分解(multiresolution signal decomposition, MRSD)一阶逼近重构光谱构造小波矩,在一定程度上克服了矩值法计算量大、高阶矩受噪声影响严重的弊端,实现了掺伪芝麻油简单快速鉴别。研究小波前两阶矩值的分类效果,结果表明,前两阶小波矩即可鉴别掺伪芝麻油; 结合邓恩分类指数(Dunn’s cluster validity index, DVI),研究了同阶小波矩分类效果及规律,确定了同阶矩中掺假芝麻油定性分析的有效及最佳矩值; 进而研究各阶小波矩的分类效果及规律,确定了可以用于掺伪麻油鉴别的各阶矩中的目标矩值及最佳目标矩值。所确定的有效矩值是针对掺伪芝麻油定性分析的有效特征,计算任一有效特征,进行谱系聚类,即可鉴别掺伪芝麻油。该方法简单、快速,可实现在线测量。文中研究思路及结论,为植物油特征提取和分类鉴别提供参考,为保障消费者权益和市场健康提供手段。
1 实验部分
从市场随机购买不同品牌、同品牌不同批次芝麻油样本Z1—Z16、菜籽油样本C1、玉米油样本Y1、大豆油样本D1和芝麻香精样本J1。样品质量均由品牌商保证。在实验室将菜籽油、玉米油、大豆油样本分别与芝麻香精样本按不同体积比例(10%~90%)混合,得到菜籽油掺伪样本JC1—JC9、玉米油掺伪样本JY1—JY9和大豆油掺伪样本JD1—JD9。将所有样本混合后放在搅拌机上搅拌10 min,而后立刻进行荧光光谱采集。样本信息如表1所列。

表1 样本信息表Table 1 Reagents and samples

图1 Z1的三维荧光光谱(a)及灰度图(b)Fig.1 The 3D fluorescence spectrum (a) andgrayscale map (b) of Z1
设定FS920荧光光谱仪激发区间250~550 nm,步长为10 nm,发射波长260~750 nm,步长为2 nm,狭缝宽度1.1 mm,对应光谱分辨率为2 nm,采集得到43个样本三维光谱数据(246×31×43)。每个样本的荧光光谱采集三次平均得到最终结果。将获得的荧光光谱进行激发发射校正预处理。数据操作皆在MATLAB R2014a环境下完成。芝麻油Z1三维荧光光谱图及对应灰度图如图1所示。
1.1 方法
1.1.1 小波多尺度分析
小波多尺度分析的严格和完整的介绍参见文献[14]。以下作理论简述:
设{V}j∈Z是L2(R2)的一个二维多尺度分析(multi-resolution analysis, MRA),尺度函数为φ,二维尺度空间为Vj=Vj⊗Vj,定义小波空间Wj,Vj+1=Vj⊗Wj。定义三个小波函数:
(1)
(2)
(3)
构成小波子空间Wj规范正交基,其收缩平移是L2(R2)的一个标准正交基。将二维图像f(x,y)∈L2(R2)多尺度小波分解得到
(4)
式中

1.2 小波矩
将样本光谱矩阵的相对荧光强度看作灰度值,则荧光光谱数据矩阵可表示为一幅灰度图。对于二维平面上的灰度图像f(x,y),它的p+q阶几何矩定义为
(5)
如果共轭滤波器H(ω)在零点处有R+1次平滑性。将图像f(x,y)在尺度函数φ(x,y),小波函数Ψ(x,y)上展开,其逼近系数为{am,n(j)},则当p+q≤R时,以小波变换逼近系数所表达的p+q阶小波矩成立[15]
(6)
1.3 谱系聚类
谱系聚类又称层次聚类,是效果较好、经常使用的聚类算法之一。其基本原理如下[16]:
设待分类的模式特征矢量为{x1,x2,…,xN},GN表示第k次合并时的第i类。则谱系聚类算法基本步骤为:

② 计算各类间距离Dij,由此生成一个对称的距离矩阵D(k)=(Dij)m×m,其中m为类的个数(初始时m=N)。

④ 检查类的个数,如果m大于2,转至步骤②; 否则停止。
1.4 模型评价
结合邓恩分类指数(Dunn’s cluster validity index,DVI)评价聚类结果[17]。设样本被分为K类,分别用Y1,Y2, …,Ym, …,Yn, …,YK各表示所划分的K个样本空间,那么DVI可表示为
(7)
即,DVI越大,则聚类样本的类间距越大,同时类内距越小,整体分类效果越好。
2 结果与讨论
用db2小波将荧光光谱进行MRSD分解。利用任一尺度逼近皆可用来构造小波矩,但由于存在吉布斯效应,随着分解尺度的增加会产生积分误差[15]。因此,选择第一尺度逼近系数重构光谱。为了增强实时性,将重构光谱归一化到0~1范围内。以芝麻油Z1为例,重构光谱及原光谱的指纹图如图2(a)和(b)所示,发射图如图2(c)和(d)所示。

图2 Z1的光谱图和第一尺度重构光谱图Fig.2 The original spectrum and the reconstructed spectrum of Z1

图3 样本矩集图示(Wp≤2,q≤2)Fig.3 The graphical of the moments (Wp≤2,q≤2)
小波矩提取光谱形状的几何信息,不同的小波矩值表征光谱不同层面的信息。构造样本的前两阶矩值小波矩:W0,0,W1,0,W1,1,W0,1,W2,0,W2,1,W3,2,W1,2,W0,2。将矩值Z-score标准化,图示化如图3所示: 芝麻油和掺伪芝麻油样本矩值特征W0,0,W1,0,W1,1,W0,1,W2,0存在重叠,无法通过谱系聚类法分类; 而矩值W2,1,W2,2,W1,2,W0,2相互分离,存在鉴别的可能性; 随着矩阶数增加,芝麻油与掺伪样本类间距有增加趋势。
定义样本间距欧式距离,类间距离差平方和。分别用九个矩值将样本进行谱系聚类。结果表明: 矩值W0,0,W1,0,W1,1,W0,1,W2,0无法鉴别掺伪样本; 矩值W2,1,W2,2,W1,2,W0,2皆可鉴别掺伪样本。以W2,2为例,其聚类树形图如图4所示: 芝麻油在1.26上聚成一类,三类掺伪芝麻油在2.78上聚成一类,合并两类则需8.45以上。结果表明,小波矩可以提取样本的有效分类特征,可实现掺伪芝麻油的分类鉴别。计算前两阶小波矩W2,1,W2,2,W1,2,W0,2中任一矩值作为特征进行谱系聚类,即可鉴别掺伪芝麻油。

图4 样本的聚类树形图(W2,2)Fig.4 The cluster tree of the samples (W2,2)
随着矩阶数的增加,芝麻油和掺伪芝麻油矩值特征的类间距有增加趋势(图3)。低阶小波矩提取光谱的整体性特征,高阶矩提取细节特征。阶数低,提取的细节信息量不足,但阶数过高,也会因高阶矩敏感于噪声和微小误差造成分类效果差。
2.1 同阶小波矩值分类效果及规律
同阶小波矩组成的矩集表征着光谱的同一几何信息,其所包含的各矩值为该几何信息的分量。计算样本各阶小波矩集进行谱系聚类,观察聚类结果,并计算DVI。以十阶矩各矩值DVI为例,十阶小波矩各矩值图示化如图5(a)所示,其DVI值如图5(b)所示。
结果表明,当p,q如图5中方式排列时,同阶小波矩分类效果呈现规律性,但低阶(阶数n≤4)和高阶(阶数n≥5)规律不一致。高阶: 如图5(b),同阶矩DVI随着q的增大,p的减小有增大趋势,即相同阶矩q值越大分类效果越好,p值越小分类效果越好。p值过大同时q值小会造成分类失败,失败案例如图5(b)中所示。其他高阶小波矩在谱系聚类时有相同规律。矩值Wp≤10, q≥2可以鉴别掺伪芝麻油称有效矩值,其中最佳有效矩值为W0,10。W0,n(n≥5)为高阶小波矩定性分析的最佳表征。低阶: 同阶矩DVI随着q的增大,p的减小呈先增后减的趋势。0阶和1阶无有效矩值。2,3和4阶的最佳有效矩值分别为W2,2,W3,3,W2,4。
2.2 不同阶矩值分类效果及规律
不同阶矩值表征着光谱不同层面的几何信息。计算各阶小波矩的最佳有效矩值,以各阶最佳有效矩值为特征将样本进行谱系聚类,并计算DVI。矩值图示化如图6(a)所示,DVI值如图6(b)所示。
如图6(a)所示,随着矩阶数的增加,样本Z3和Z5的矩值特征与其他芝麻油样本差异逐渐增大,导致高阶小波矩分类效果不佳。高阶矩提取细节特征,对噪声和微小差异存在放大作用。如图6(b)所示,DVI随着阶数的增加先增加后减小,最后趋于稳定。随着阶数的增加,分类效果渐佳,但阶数过高会造成样本Z3和Z5与其他芝麻油样本差异化,造成分类效果变差。W0,q≥2可以鉴别掺伪芝麻油,称为目标矩值,其中W0,6为最佳目标矩值。W0,6聚类树形图如图7所示: 芝麻油1.24以上聚成一类,三类掺伪芝麻油1.13以上聚成一类,合并两类则需8.94以上。文中所确定的小波矩的有效及目标矩值是鉴别掺伪芝麻油样本的有效特征,直接计算样本的任一有效特征进行谱系聚类,即可准确鉴别掺伪芝麻油。

图5 十阶小波矩各矩值分类效果及规律Fig.5 The DVI of the tenth order wavelet moments
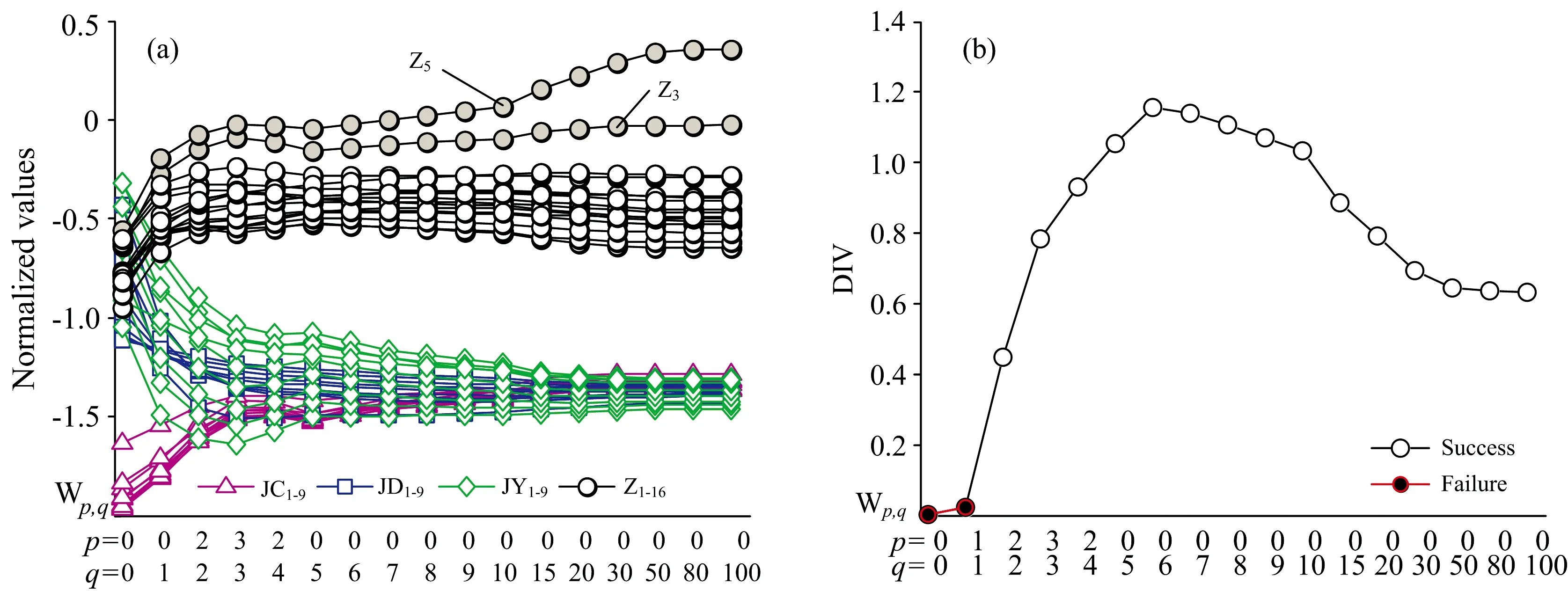
图6 不同阶小波矩分类效果及规律Fig.6 The DVI of different order wavelet moments

图7 各阶小波矩中最佳有效矩值W0,6聚类树形图Fig.7 The cluster tree of optimal target WMs (W0,6)
3 结 论
提出将小波矩应用到三维荧光光谱,以有效矩值为特征进行谱系聚类,实现了掺伪芝麻油样本的鉴别。以MRSD的一阶逼近重构光谱,去除了噪声,减少光谱数据量72.4%,增加了矩值法的抗噪稳定性和实时性。通过研究同阶矩及各阶矩分类效果及规律,确定了可以鉴别掺伪芝麻油的小波矩值。该方法简单快速有效,利用任一有效特征即可鉴别掺伪麻油。研究思路及结论为矩值法应用到三维荧光光谱提供参考。为质监部门及生产企业提供油品检测和鉴定手段。
