拟非扩张映射分裂公共不动点问题的收敛性定理*

李 蓉何振华

(广西财经学院,a.教务处,b.信息与统计学院,广西 南宁 530003)

0 引言

假设H是实Hilbert空间,其零向量用θ表示,内积和范数分别是〈·,·〉,‖·‖.称映射T:H→H是非扩张映射,如果‖Tx-Ty‖≤‖x-y‖,x,y∈H.称映射T:H→H是拟非扩张映射,如果‖Tx-p‖≤‖x-p‖,x∈H,p∈F(T),F(T)≠Ø是T的不动点集.

设H1,H2是实Hilbert空间,A:H1→H2是有界线性算子,T1:H1→H1,T2:H2→H2是非线性映射,且F(T1)≠Ø,F(T2)≠Ø.分裂公共不动点问题通常指的是这样的问题:找p∈H1使得T1p=p和T2Ap=Ap(当T1,T2是单值映射),或者p∈T1p和Ap∈T2Ap(当T1,T2是集值映射).

数学上不同空间下的分裂问题首先在文献[1]中出现,而以色列学者Censor教授在文献[2]中正式给出了分裂公共不动点问题的定义.分裂不动点问题在图像恢复中有重要的应用,因而关于此类问题得到众多学者的关注和研究.当然大部分学者的研究成果更主要侧重于基础研究,并非直接应用到图像恢复问题的求解中.分裂不动点问题除了在图像恢复问题中有用之外,对此问题本身的研究也是具有重要意义的,因为求解此类问题用到的不动点算法,可以实现一个算法求解多个问题的目的,这是通常的多项式算法所不具备的.因此,不动点算法除了在方法论上提供一种求解问题近似解的方法,还具有其他算法没有的优点.

在分裂不动点问题的研究中,法国学者Moudafi教授发表了一系列分裂公共不动点问题的研究成果,引发了大量的后续研究.日本的Takahashi教授、韩国的Yeol Je Cho教授、中国的张石生教授等,都是研究分裂公共不动点问题的著名专家,他们也是研究这类问题的引领者.在文献[3]中,作者建立如下的迭代算法:

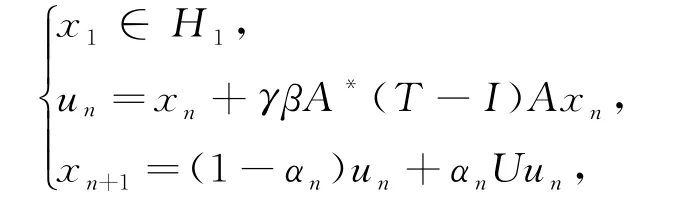
其中β∈(0,1),αn∈(0,1),γ＞0,U和T分别是不同空间中的拟非扩张映射.在合适的条件下,作者证明上述序列{x n}弱收敛到分裂公共不动点p∈Ω,其中

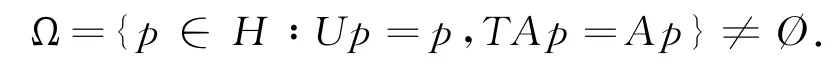
注意到,上述给出的序列{x n}仅仅具有弱收敛性质,为了得到强收敛算法,文献[4]建立了如下的迭代算法:

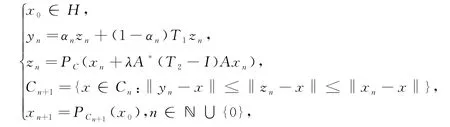
其中T1∶H→H和T2:H1→H1分别是不同空间中的拟非扩张映射,H和H1分别是Hilbert空间.在合适的条件下,作者证明上述的投影序列{x n}强收敛到分裂公共不动点p∈Ω,其中Ω={p∈H:T1p=p,T2Ap=Ap}≠Ø.

前面提到的分裂公共不动点问题,是关于两个不同空间中的分裂公共不动点问题,这类问题已经得到众多学者的研究,取得了许多研究成果.他们建立了Man迭代算法、Ishikawa迭代算法、黏性迭代算法、CQ 迭代算法等算法用于求解此类问题的近似解.这些算法中,有些是强收敛的,有些是弱收敛的.空间形式也从Hilbert空间推广到Banach空间,例如文献[2-8]及其参考文献.从目前查阅到的文献看,考虑比较多的分裂公共不动点问题都是关于两个不同空间中的分裂公共不动点问题,关于三个或者三个以上不同空间的算子的分裂公共不动点问题,研究成果比较少.本文将考虑三个不同空间的分裂公共不动点问题:

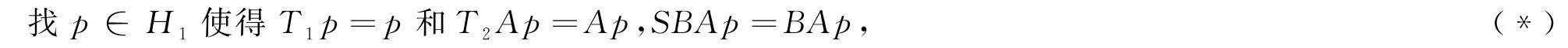
其中,A:H1→H2,B:H2→H是有界线性算子,其伴随算子分别是A*,B*,算子T1:H1→H1、T2:H2→H2、S:H→H是拟非扩张映射,且Ω={p:T1p=p,T2Ap=Ap,SBAp=BAp}≠Ø.

在不动点问题的求解中,建立迭代序列使其收敛到算子的不动点是常用的方法.为求解问题(*),本文将建立迭代序列,在合适的条件下,证明其强收敛或者弱收敛到问题(*)的解.

1 预备知识

设H是实Hilbert空间,C是H的闭凸子集.P C表示H到C的投影算子,它具有如下的性质:

(1)z=P C(x)⇔〈x-z,z-y〉≥0,∀y∈C,

(2)‖y-P C(x)‖2+‖x-P C(x)‖2≤‖x-y‖2,∀x∈H,y∈C,

(3)〈x-y,P Cx-P Cy〉≥‖P Cx-P Cy‖2,特别‖P Cx-P Cy‖≤‖x-y‖,∀x,y∈H,即投影算子是非扩张映射.

引理1 设H是实Hilbert空间,α∈[0,1],则下面结果是众所周知的:

(i)‖x+y‖2≤‖x‖2+2〈y,x+y〉,

(ii)‖x-y‖2=‖x‖2+‖y‖2-2〈x,y〉,

(iii)‖αx+(1-α)y‖2=α‖x‖2+(1-α)‖y‖2-α(1-α)‖x-y‖2.

定义1[3]设C是H的闭凸子集,T:C→C.称映射T是半闭的,如果对于C中的点列{x n},,且{x n}弱收敛到z,则有Tz=z.

例1[8]设C=[0,1],H =R(实数集),定义T:C→C为

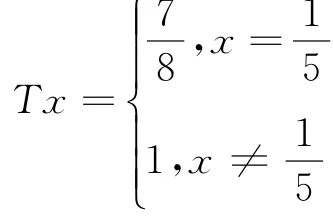
则T是半闭的拟非扩张映射.

例2[8]设C=[0,+∞),H =R(实数集),定义T:C→C为

则T是拟非扩张映射,但不是半闭的.

一个Banach空间(X,‖·‖)被称为是满足Opial条件[9]的,如果对于X中任一弱收敛到x∈X的序列{x n}满足

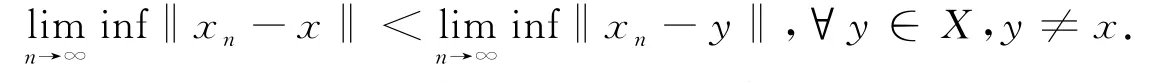
特别,每一个Hilbert空间都是满足Opial条件的.

2 主要结果

在这一节中,假设H i的内积和范数分别是的内积取为〈x,y〉3=〈x1,y1〉1+〈x2,y2〉2,其中x=〈x1,x2〉,y=〈y1,y2〉∈H3.

设A:H→H1,B:H1→H2是有界线性算子,定义Cx=(Ax,BAx),x∈H,则显然C也是有界线性算子.

定理1 设A:H→H1,B:H1→H2是有界线性算子,其伴随算子分别是A*,B*,S:H→H,T1:H1→H1,T2:H2→H2

是半闭的拟非扩张映射,且Ω={p∈H:Sp=p,T1Ap=Ap,T2BAp=BAp}≠Ø.

设x1∈H,序列{x n}按照以下方式产生:

则{x n}弱收敛到p∈Ω,其中C*是C的伴随算子,

证明:(i)先证明{‖x n-p‖}是收敛序列,其中p∈Ω.

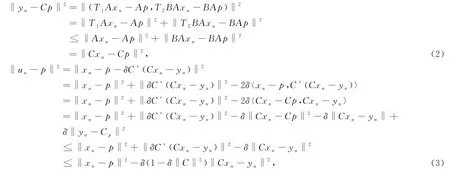
因此,

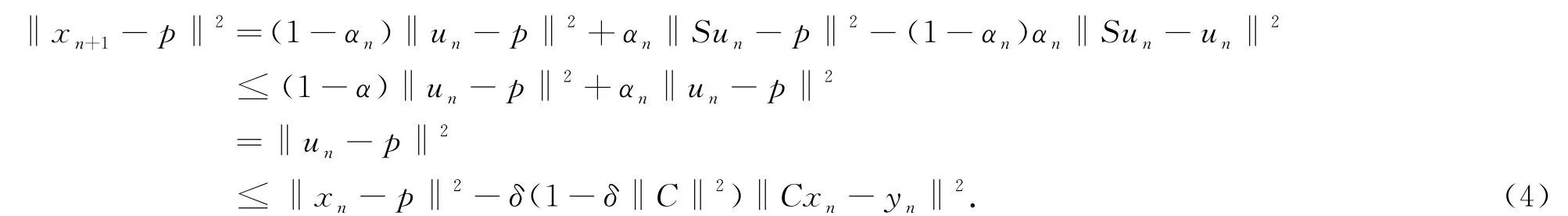
上式说明{‖x n-p‖2}是单调递减序列,因而极限存在,即{‖x n-p‖}是收敛序列.并且由此可得

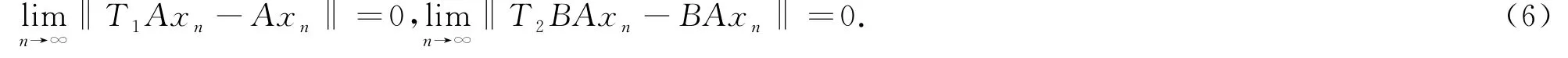
(ii)因为{‖x n-p‖}收敛,因此{x n}是有界序列,从而{x n}有弱收敛的子列.假设{x n j}和{x mk}是{x n}的两个弱收敛子列,分别弱收敛到x*和y*,则必有x*,y*∈Ω.事实上,显然{u n j}、{u mk}、{Ax n j}、{Ax mk}、{BAx nj}、{BAx mk}分别弱收敛到x*、y*、Ax*、Ay*、BAx*、BAy*,因此根据S,T1,T2是半闭映射以及(5)式和(6)式可知,x*,y*∈Ω.

现在证明x*=y*.如果x*≠y*,则根据Opial条件可知

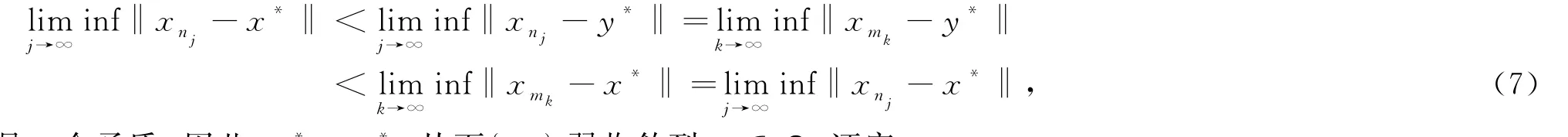
这是一个矛盾.因此,x*=y*.从而{x n}弱收敛到p∈Ω.证完.

推论1 如果在定理1中,T2=B=I是恒等算子,H1=H2,其他条件不变,序列{x n}按照以下方式产生:

则{x n}弱收敛到p∈Ω,Ω={p∈H:Sp=p,T1Ap=Ap}≠Ø.其中A*是A的伴随算子,0＜a≤αn≤

注1:推论1是文献[3]中定理2.1的结果,因此定理1推广了文献[3]的结果.

如果说在定理1中讨论的是不同空间下的分裂问题,那么在定理1中,H1=H2=H,我们将得到下面的同一空间的分裂问题.

推论2 如果在定理1中,H1=H2=H,其他条件不变,序列{x n}按照(1)式产生,则{x n}弱收敛到p∈Ω.

定理1是弱收敛定理,实际上,从理论的角度看,强收敛定理应用更为方便一些.下面介绍一个强收敛定理.

定理2 设A:H→H1,B:H1→H2是有界线性算子,其伴随算子分别是A*,B*,

是半闭的拟非扩张映射,且Ω={p∈H:Sp=p,T1Ap=Ap,T2BAp=BAp}≠Ø.

设x0∈C1=H,序列{x n}按照以下方式产生:

则{x n}弱收敛到p∈Ω,其中C*是C的伴随算子,

证明:(i)先证明{C n+1}是非空的闭凸集合列.设p∈Ω,则根据(3)式,‖u n-p‖ ≤‖x n-p‖.

此外,易知‖z n-p‖≤‖u n-p‖,因此Ω⊂C n+1,即{C n+1}是非空的集合列.对于任意的p1,p2∈C n+1,∀r∈[0,1],因为

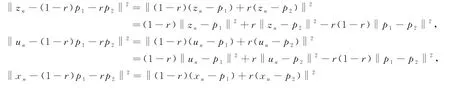
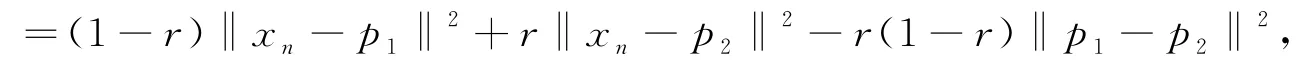
所以 ‖z n-(1-r)p1-rp2‖ ≤‖u n-(1-r)p1-rp2‖ ≤‖x n-(1-r)p1-rp2‖.

即(1-r)p1+rp2∈C n+1,这说明{C n+1}是凸的集合列.设{p k}⊂C n+1,且{p k}收敛到p,即limk→∞‖p k-p‖=0,易证p∈C n+1,因此{C n+1}是闭的集合列.综上,{C n+1}是非空的闭凸集合列,从而序列{x n}是存在的.

(ii)证明{x n}是Cauchy序列.注意到x n+1,p∈C n,根据{x n}的定义,可知

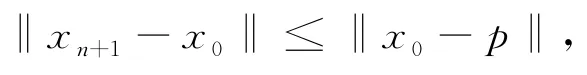
因此序列{x n}是有界的.又

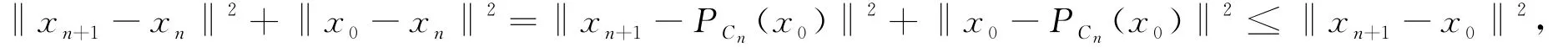
因此,{‖x n-x0‖}是单调递增序列,这说明存在.注意到

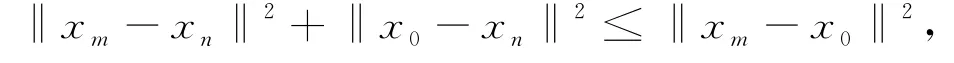
于是当n,m→∞时,‖x m -x n‖ →0,因此{x n}是Cauchy序列.

(iii)证明{x n}强收敛到Ω的一个元.因为{x n}是Cauchy序列,因此可以设x n→p*,n→∞.现在证明p*∈Ω.

根据(9)式可知

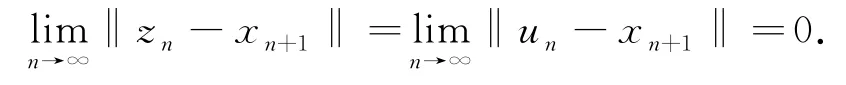
于是由

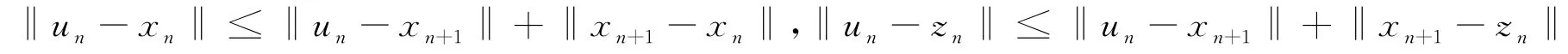
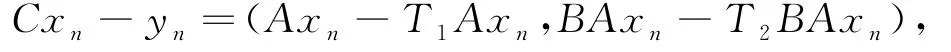
因为x n→p*,n→∞,所以

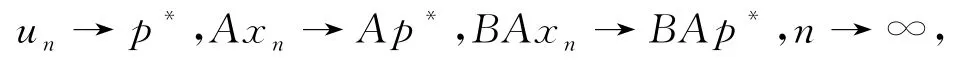
这样根据S,T1,T2的半闭性可知Sp*=p*,T1Ap*=Ap*,T2BAp*=BAp*,即p*∈Ω.证完.

推论3 如果在定理2中,T2=B=I是恒等算子,H1=H2,其他条件不变,序列{x n}按照以下方式产生:

则{x n}强收敛到p∈Ω,Ω={p∈H:Sp=p,T1Ap=Ap}≠Ø,其中A*是A的伴随算子,0＜a≤αn≤

如果在定理2中,H1=H2=H,我们将得到下面的同一空间的分裂问题的强收敛定理.

推论4 如果在定理2中,H1=H2=H,其他条件不变,序列{x n}按照(9)式产生,则{x n}强收敛到p∈Ω.

3 结论

在本文中,我们讨论了三个空间的分裂公共不动点问题,给出了两个收敛算法,一个是强收敛算法,另一个是弱收敛算法.我们的结果推广和改进了一些文献的结果.