林用六轮摆臂底盘转向稳定性分析与控制策略

程钰晶， 王 典， 刘晋浩， 黄青青

(北京林业大学林业与环境特种装备研究中心，北京100083)

为了提高我国林区的机械化水平，改善林区机械作业条件，开发适用于林区的机械作业底盘是极其必要的[1-4]。林用六轮摆臂底盘可针对崎岖不平的林区地形环境进行主动越障以及转向调平。为提高六轮摆臂底盘在林间斜坡路面进行转向作业时的稳定性，找到适用于林用底盘的稳定度理论并开发适合的控制策略具有非常重要的意义[5-6]。朱清源通过互补滤波算法，测量稳态边缘角并作为侧翻稳定性的判断指标[7]。Mian Ashfaq Ali 等通过侧向加速度和测量侧倾角的信息，使用潜在的场函数进行稳定性指标判断[8]。李学飞等通过二级稳定度理论确定轮式装载机的侧翻稳定性并通过模糊神经理论进行控制调平[9-11]。欧阳益斌等[12]通过纵向稳定性以及纵向滑移角等来判断抚育机履带底盘稳定性。田海波等[13-14]将动态能量稳定边界法与稳定锥方法相结合得到了动态能量稳定锥方法，并对一种具备6种构型的机器人进行了稳定性评价。肖藩通过模糊PID控制方法对三自由度并联机构进行自动调平控制并验证模糊PID-Smith预估器具有良好的调平控制效果[15]。吉林大学王忠山针对山地拖拉机设计了一款实现车身姿态自调整的调平液压系统，通过调平液压缸内流量、压力，液压缸活塞杆位移、速度等曲线，得知横坡倾角≤15°工况下车身调平液压系统的稳定性能够满足工作要求[16]。东北林业大学曹时凯设计了一款车扫描仪车载调平机构，通过激光扫描仪对斜坡坡度、灌木高度、树高和树木坐标等数据的采集和分析，确定了调平平台调平的角度[17]。吉林省农业机械研究院徐峰等研究了一种山地拖拉机调平系统，但由于动态稳定性不好，还未应用于生产实际[18]。本文提出的六轮摆臂底盘与四轮底盘相比，将门式摆动桥摆动部分设计为拱形，存在三个自由度前后车架自由摆动，实现了桥体离地间隙的优化，且能通过位姿调整保证轮胎全部着地，提高了本身底盘的稳定性。与履带底盘相比，大大减小了对林区地表的伤害，行驶速度加快，适合公路行驶和长途运输[19]。本文针对一款林用六轮摆臂底盘，建立底盘稳定度模型，通过建立摆臂液压缸的控制模型，实现底盘的防倾翻并提高其转向行驶的稳定性。

1 六轮摆臂底盘稳定度模型

优化底盘质量重新建立林用六轮摆臂底盘虚拟样机[20]，样机建模及样机参数如图1及表1所示，其中液压缸径D=80 mm，推力70 kN，杆径d=55 mm，拉力37 kN。针对虚拟样机，本文采用旋量理论[21-24]建立六轮摆臂底盘运动过程中的运动学方程，为求得六轮摆臂底盘从初始基坐标系运动到末端工具坐标系的运动学方程，采用机器人运动学正解指数积公式：

(1)

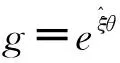
图1 Solidworks环境下六轮摆臂底盘虚拟样机

表1 底盘样机整体参数表

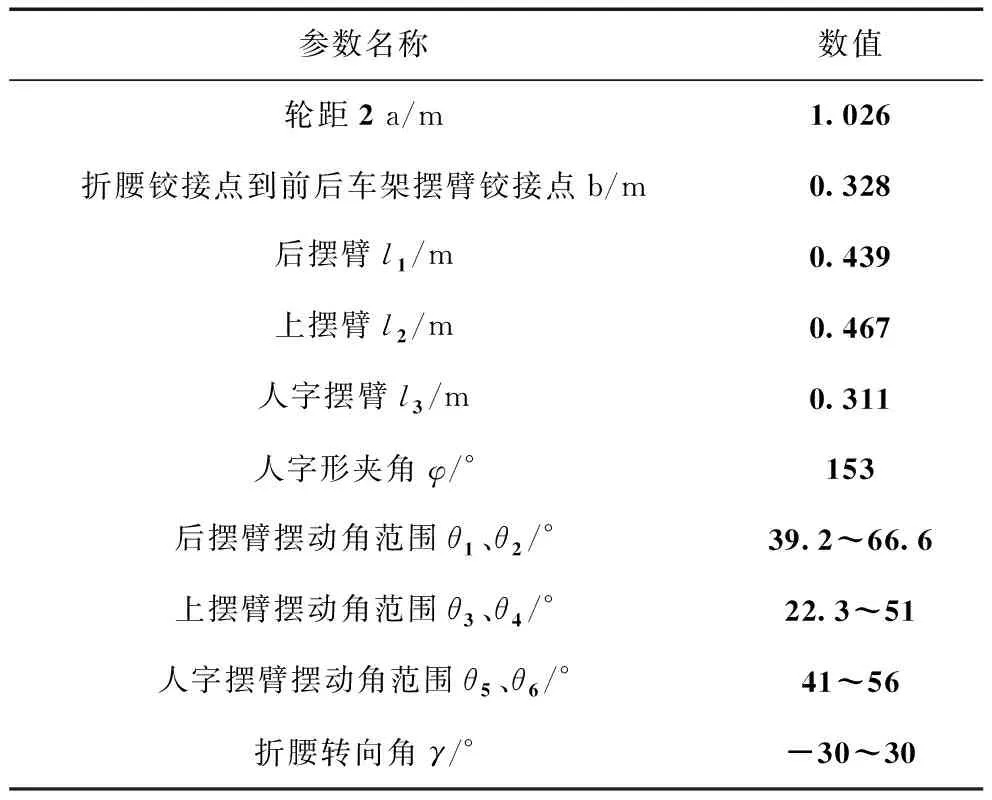
参数名称数值轮距2 a/m1.026折腰铰接点到前后车架摆臂铰接点b/m0.328后摆臂l1/m0.439上摆臂l2/m0.467人字摆臂l3/m0.311人字形夹角φ/°153后摆臂摆动角范围θ1 、θ2/°39.2～66.6上摆臂摆动角范围θ3 、θ4/°22.3～51人字摆臂摆动角范围θ5 、θ6/°41～56折腰转向角γ/°-30～30

由式(1)求解出各个摆臂绕基坐标旋转以及平移的运动学矩阵，分别将前车架右侧上摆臂与人形摆臂、前车架左侧上摆臂与人形摆臂、折腰转向与后车架右侧摆臂、折腰转向与后车架左侧摆臂看作一个整体，通过正解指数积公式得到每一个整体部分旋转以及平移时的位姿变化，以此获得基坐标系到轮胎接地点末端的运动学变化矩阵，最终可获得底盘轮胎接地点坐标。六轮摆臂底盘结构参数如图2所示。

图2 六轮摆臂底盘结构参数

求得六轮摆臂底盘的运动学模型为：

(2)

(3)

(4)

(5)

林用六轮摆臂底盘在斜面上转向行驶时，前后车架中间连接的折腰转向角与倾翻轴同侧不利于底盘的稳定，而倾翻轴与折腰转向角对侧则有利于底盘的稳定，故本文只考虑底盘向斜面下方转向的侧翻工况。

林区道路的平均坡度为26.6°[25-26]，小局部地段形成30°～45°的陡坡[27]，为适应林用六轮摆臂底盘在东南林区的坡道路面上行驶，本文通过二级稳定度理论[28-32]进行稳定度计算并仿真底盘在极限30°斜面上的转向行驶稳定性。六轮摆臂底盘斜面折腰向下转向工况如图3所示。

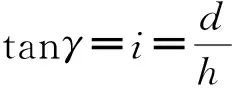
(6)

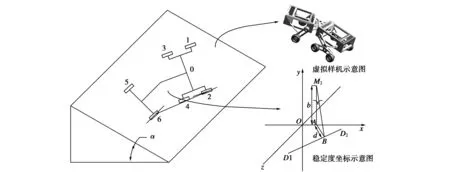
图3 六轮摆臂底盘斜面折腰向下转向工况

2 六轮摆臂底盘满载侧翻稳定性

六轮摆臂底盘沿斜坡水平方向行驶时，前进速度以及折腰转向角度两个因素可能会造成底盘稳定度波动，故在底盘满载工况下进行转向过程中，探讨折腰转向角度以及前进速度对底盘稳定性所造成的影响。六轮摆臂底盘样机如图4所示。

图4 六轮摆臂底盘样机

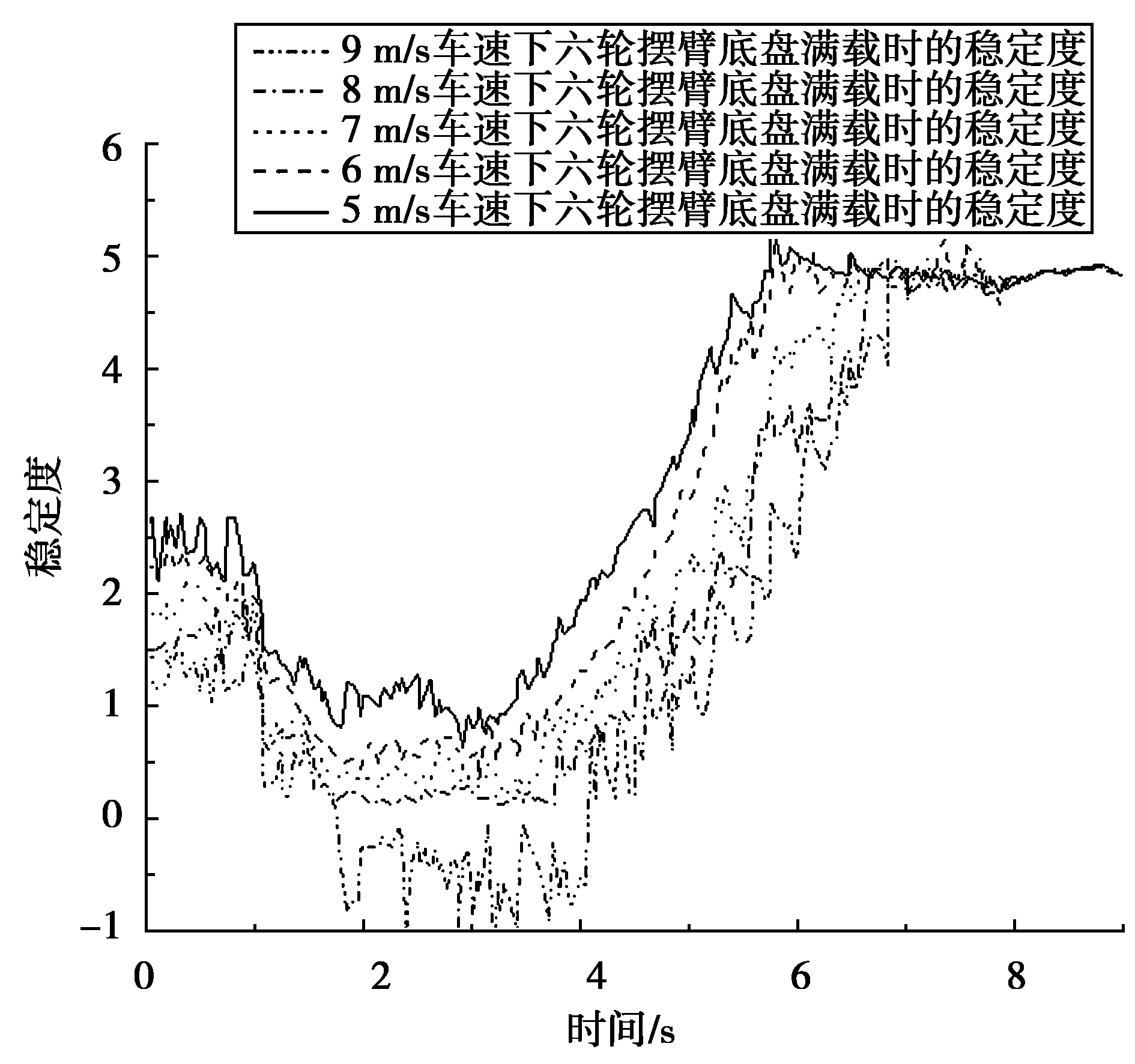
图5 折腰转向30°时不同速度下的稳定度变化

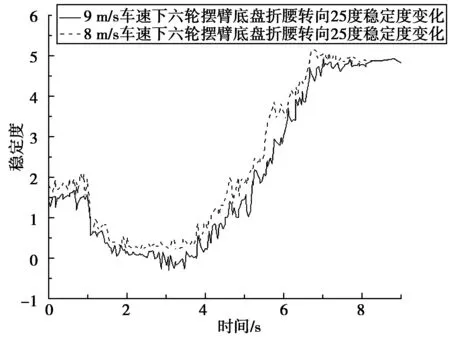
图6 折腰转向25°时不同速度下的稳定度变化

由图5得知当六轮摆臂底盘在坡面上以30°折腰转向角转向行驶过程中，通过输出的稳定度得知速度为7 m/s时底盘仍处于稳定状态，速度为8 m/s时达到阈值，9 m/s时底盘发生倾翻。故当折腰转向角为30°时仅仿真速度为8 m/s及9 m/s的工况进行对比。

由图6可知六轮摆臂底盘沿斜坡水平方向行驶并向前进方向左侧转向过程中，当折腰转向角度达到 25°、车速达到8 m/s时底盘处于稳定状态；车速到达9 m/s时底盘发生倾翻，此时最低稳定度为-0.2。

3 控制工况下六轮摆臂底盘侧翻稳定性

液压缸抬升下降位置变化如图7所示。由图7可知液压缸在抬升及下降过程中液压缸的伸缩会导致摆臂在基坐标系下与车架间夹角θ的变化，以此稳定度i会发生变化。六轮摆臂底盘的轮腿有抬升和下降两种工作状态，通过液压缸的伸缩完成轮腿带动车架的抬升以及下降的动作。通过建立几何关系可以得到轮腿抬升下降造成的摆臂角度变化与车架位置变化的关系。

图7 液压缸抬升下降位置变化

通过对图7的几何分析，可以得到轮腿摆角变化量Δθ与液压缸变化量之间的关系：

(7)

(8)

Δθ=θ-θ′

(9)

B′C′2=AB2+AC2-2×AB×AC×cosθ′

(10)

BC2=AB2+AC2-2×AB×AC×cosθ

(11)

故得到轮腿摆角变化Δθ与车架抬升下降变化量Δy之间的关系：

(12)

其中，Δθ为摆臂角度变化量，Δy为车架上升下降变化量。Δθ为正时表示液压缸伸长，车架上升，摆角增大；Δθ为负时表示液压缸缩短，车架下降，摆角减小。故上述公式可以通过车架抬升以及下降的高度反解出摆臂角的变化，继而求得液压缸的伸缩量。通过模糊控制结合六轮摆臂底盘摆臂液压缸的反解函数，对油缸长度、伸缩速度进行控制，从而获得需要的运动效果，通过Adams/Simulink联合仿真得到转向模糊控制策略，输出包括底盘稳定度、液压推杆长度。模糊控制规则表见表2，联合仿真控制线路图如图8所示。

表2 模糊控制规则表

Lt L1L2L3L4L5L6L7SPEEDMMNSNSNSNBNBFIRSTPSMNSNBNBNBNBSECONDPSPSPSMNSNBNBENDPBPSPSMNSNBNB

图8 联合仿真控制线路图

通过将PID控制以及模糊控制下输出的底盘稳定度与没有控制的稳定度分别进行对比，得到不同转向角度下的稳定度变化情况，分别如图9～12所示。

图9 25°转向角、9 m/s车速下前后车架稳定度变化

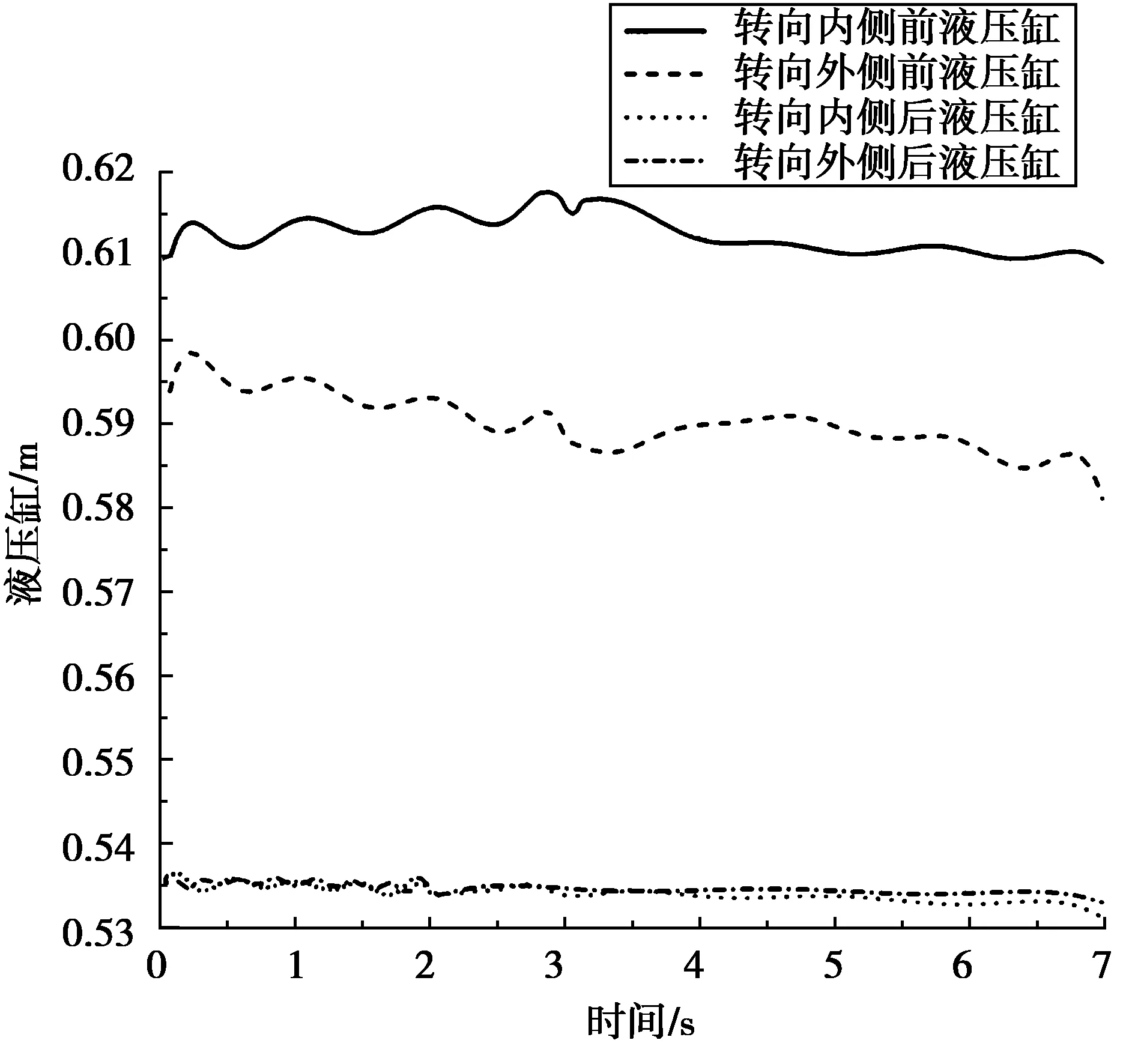
图10 25°折腰转向角工况下液压缸长度变化曲线

由图9以及图11可知，六轮摆臂底盘前进速度为9 m/s、转向角度分别为25°以及30°时，对比三条稳定度变化曲线，发现在模糊控制下稳定度相比于PID控制得到了微小提高，且液压缸响应较PID控制缓慢，车架波动较为缓慢，有益于提高舒适性，由此证明六轮摆臂底盘在极限30°林地路面下的控制策略起到作用。加上模糊控制后，在25°折腰转向角的工况下稳定度相比PID控制，稳定度约提高3%，由图10可知内侧液压缸变化范围为61.0～61.6 cm，外侧变化范围为58.7～59.8 cm；30°折腰转向角工况下稳定度提高了2%，由图12可知内侧液压缸变化范围为61.2～61.8 cm，外侧变化范围为58.5～59.6 cm。

图11 30°转向角、9 m/s车速下前后车架稳定度变化

图12 30°折腰转向角工况下液压缸长度变化曲线

4 小结

通过旋量理论建立林用六轮摆臂底盘的运动学模型，通过运动学模型以及二级稳定度理论求解出林用六轮摆臂底盘的稳定度，并将仿真得到的数据代入理论方程中求解出满载工况下的稳定度。满载底盘在沿斜坡水平方向行驶并向直行方向左侧转向过程中，当折腰转向角度达到25°、车速达到8 m/s时底盘达到阈值，9 m/s时底盘会发生倾翻，当斜面为30°、底盘车速达到8 m/s时底盘就会发生倾翻。

针对稳定度波动幅度大以及发生倾翻的工况，建立林用六轮摆臂底盘在30°斜面上转向行驶过程中六轮摆臂底盘摆臂液压缸的控制模型。通过PID控制下的Adams/Simulink联合仿真，在无控制策略时，六轮腿式底盘在满载条件下最大行驶速度为8 m/s；加入控制策略后，在车速9 m/s的工况下，折腰转向角为25°时底盘稳定度最低约为0.371，约提升13%，折腰转向角为30°时，底盘稳定度最低约为0.214，整体稳定度得到10%的提升。实验证明六轮摆臂底盘摆臂液压缸的控制理论能有效提高底盘稳定性，实现底盘平稳转向。