基于红外成像的小型化稳定平台参数辨识

郭雪峰，林 宇

基于红外成像的小型化稳定平台参数辨识

郭雪峰，林 宇

（昆明物理研究所，云南 昆明 650223）

针对红外成像的小型化稳定平台参数辨识的问题，对系统中非线性因素进行尽可能抑制，并在高速环境下对系统进行辨识。在辨识过程中，利用伪随机信号（Pseudo random binary signal，PRBS）作为调制的输入电压信号对系统激励，相应的系统输出响应为速度信号，并应用增广最小二乘方法辨识线性离散模型参数，最后通过参数化和非参数化两种方式，对辨识模型的精确度进行了验证。结果表明：辨识得到的用来衡量实际系统输出随输入变化的传函关系的参数模型，能够反映真实系统的动态特性，满足辨识精度要求。

稳定平台；参数辨识；开环辨识；增广最小二乘法

0 引言

基于红外探测成像的稳定平台是利用机电控制达到隔离载体扰动，从而保持红外探测器光轴/视轴在惯性空间指向稳定的系统。为了保证对目标的成像质量，并且满足现今战场对武器体积小，重量轻，机动特性好的需求[1-2]，在已经对小型化稳定平台结构优化以及器件合理选型等的前提下，为了能更大程度提升后续动态性能和隔离性能，就需要对系统的特性进行研究，再通过设计控制器进行改善。

小型化稳定平台是属于集平台载荷，框架系统，驱动与控制系统等于一体的复杂系统。如图1所示，主要由PWM（Pulse Width Modulation）功率放大器、直流电机、负载、传感器等共同组成，整个控制系统在输入信号作用下进行响应，输出响应的类型和特征能够反映系统特性。因此针对其复杂的系统组成，只能通过理论建模或实验建模两种方式对系统特性进行描述[3-4]。由于，在平台的连接轴承、伺服电机电刷、动摩擦件及导轨等部件中，存在明显的非线性特征。相比理论建模对于实际系统的刻画并不精确，并且需要繁重的推导过程等缺点，实验建模并不完全依赖对象先验知识的获取，通过图表或参数方程都能反映系统输入输出之间的关系。

在高频激励信号作用的动态辨识环境下，除上述非线性因素外，包括残余噪声，线绕力矩等在内的更多误差源和非线性因素对系统的运动特性产生干扰，且不易用具体参数模型进行描述，由此得到的伺服控制系统的实际响应，与根据各机电环节固有参数进行理论推导的模型的响应相比差别很大，用来辨识的输入输出数据都是受非线性因素影响的非理想信息，如何利用受污染的数据辨识出无偏的参数，这也是包括稳定平台在内的机电系统辨识的共有难点。

图1 待辨识的稳定平台实物图

1 小型化稳定平台辨识现状及分析

针对小型稳定平台这类具有有限行程的机电系统的辨识研究，大多数文献都集中于对电机执行器件的参数辨识，如图1为待辨识的小型化稳定平台，具体问题表现在以下方面：

1）伺服系统工作时，不可避免地需要克服因动密封而引入的较大摩擦力矩和其他线绕力矩等非线性因素，基于LTI（Liner time invariant）系统的时域和频域辨识方法所用的速度或加速度数据都是受非线性因素影响的非理想数据，从而导致辨识结果产生较大的误差。

2）现有的时域辨识算法通常采用充分激励后，对采集得到的速度及加速度信息进行辨识，小型稳定平台因受行程范围的局限，当在小幅值输入信号作用下，系统需要克服一定摩擦力，而达不到能真实对应输入信号作用下速度值，当输入信号幅值过大时，运动范围超出有效行程而与框体撞击，完全破坏固有的运动状态，采集到的信息完全不能表征原有系统，而使辨识失效，同时，一般的光电系统具有充分的运动空间，能够输入幅值足够大的激励信号，相对能满足更高的信噪比，这也使得小型化稳定平台辨识易受量化噪声的影响。

其次，为了使辨识出的模型不仅具有与原系统近似的动态特性，还要保持一致的稳态值，所以系统在辨识过程中要有足够的空间位移渡过暂态过程，进入稳态过程，但运动范围的限制会使系负载最终未能达到稳态的速度终值，这样辨识出的参数模型与真实系统相比会有稳态误差。

3）应用优化算法在对非线性参数模型进行搜索时，不仅要对模型参数进行辨识，如果以stribeck摩擦模型为例对系统运动时摩擦特性进行描述时，还要对摩擦模型中的库伦摩擦力，静摩擦力，曲线系数，防死区推力等参数进行辨识[5]，尤其当系统运行在不同方向时，要辨识的参数数目更是加倍，辨识效率随其数目的增多而大大降低，算法很难收敛到能够满足所有情况的全局最优值而失效，辨识的参数也就无法真实反映实际系统的物理参数。有必要对如何解决上述依次存在的辨识问题，进行讨论。

按照现已探索出的摩擦力与速度的函数模型，如图2所示。

基本所有机械系统都不可避免会受到非线性的影响，属于非线性系统。小型稳定平台由于要满足动态快，高精度等控制性能，需要在高速状态下工作，但受限于轻量化的机械结构特性，使得转动惯量远低于其他大型稳定平台，在整个运动范围内很容易受摩擦，低频干扰等非线性因素的影响，很难近似为一个线性化系统进行描述。以摩擦力为例，它是对系统运动特性影响较大且不能彻底消除的因素之一，用现已探索出的摩擦力与速度的关系模型来描述，可以分为以下4个阶段：

Ⅰ.在静摩擦和预滑位移阶段，由于预滑位移的存在而产生了弹性变形，因而表现出弹簧特性。此阶段的摩擦力不依赖于速度，主要体现与速度无关的静摩擦特性。

Ⅱ.在边界润滑阶段，摩擦力主要是由固体间的剪切作用引起的，其与低速爬行现象存在着密切的关系。

Ⅲ.在部分流体润滑阶段，随着滑动速度的增加润滑膜变得越来越厚，使得固体间突起的接触数量减少。因而摩擦力呈现负斜率特性。

Ⅳ.在全流体润滑阶段，粘滞摩擦逐渐起主导作用，固体接触影响较小，摩擦力会随着速度的增加而增大。

图2 摩擦力与速度关系

如果系统工作在低速区，摩擦力受速度变化的影响呈现明显的非线性特性，工作在高速区时，摩擦与速度的关系可近似为比例关系，如果在低速区对系统辨识，由于辨识出的参数化模型只能反映系统的线性特征，而非线性的干扰使得模型对原系统的刻画不精确，为了更大程度使系统受非线性影响减少，要保证在高速区对系统进行辨识。通常控制方式下，待辨识系统都会根据输入信号的幅值大小做出对应的速度响应，增大输入电压，速度值也随之提高，也就意味着增大输入电压增益可以使系统工作在高速环境下。

这样，通过一定线性化处理，最大程度上避免非线性因素影响，并考虑将内部的各种非线性误差因素看作系统中的统一的一个干扰源，这部分对系统的影响会叠加在系统理想输出上，最终辨识得到的参数反映输入信号与输出信号之间随时间变化的关系，不考虑内在变量的影响，无需使用已有的摩擦模型进行描述补偿[5]，也不用对多个随机的干扰进行单独建模分析，减少了不确定因素数量，大大减小了辨识难度，是在研究中可以实现的一种方法。

2 伺服机构动力学建模

动力学建模属于理论建模，虽然这种方式对于实际系统的刻画并不精确，并且需要繁重的推导过程，尤其是对于高阶多参数的系统更为不利，但可以侧面确定模型阶数，是否含有积分环节等特征。待辨识对象是由脉宽调制功率放大器、执行机构、负载、传感器共同组成的复杂系统，惯量盘作为唯一负载加在俯仰框架上，直流力矩电机和平台负载的等效电路图如图3所示。

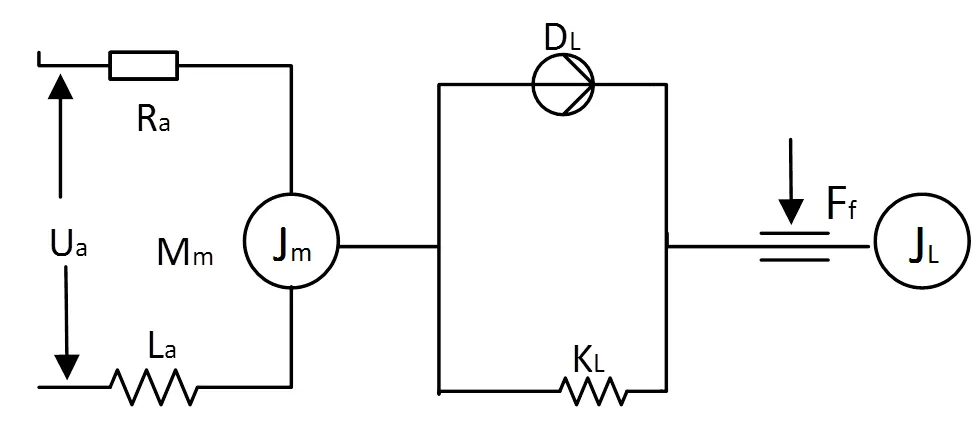
图3 电机和负载等效电路图

由直流力矩电机电枢的电压平衡方程、反电势方程和力矩电机电磁作用方程可得：

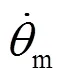
由电机动力学原理可得：

同时，所用的PWM式功率放大器的带宽远大于控制系统的工作带宽，其用来表示输出整流电压与微小控制输入电压之间的函数关系可以忽略延迟，仅用下式表达：

式中：pwm表示PWM功率放大器的对输入电压的放大系数。摩擦是通过速度对电枢电流响应施加干扰的。当系统在单向宏观滑动运动时（即增大增益，使对象快速度过启动期的非线性摩擦力作用区），这时摩擦工作特性可用下式简单的库伦摩擦及粘滞摩擦描述[6]，使速度满足阈值条件，将摩擦尽可能线性化为常值耦合到模型参数中辨识：

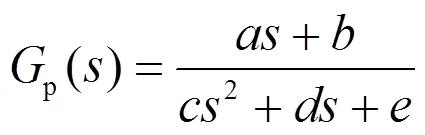
则只需对，，，，这5个参数进行辨识，就可以直接用来表征电机携负载从输入电压信号到输出速度响应的参数模型。

3 开环辨识分析与实验

开环条件下，系统会按照所施加电压信号随时间变化的规律做出直观响应，由于缺少反馈的引入，稳定平台的俯仰框架上的负载运动只能由输入信号一个变量控制，考虑到平台伺服机构存在的有限行程限制，故对光电稳定平台而言，其辨识过程还需满足以下约束条件：

其中的参数不再与前述分析的连续模型的参数一一对应。

用做激励的伪随机信号（PRBS）是由矩形脉宽组成的随机序列，单个的矩形脉宽的周期决定了整个序列段最大的变化频率max，参考带宽的范围，最终辨识的模型在此范围内的动态特性要与实际系统近似，因此，在此频率范围内，激励信号的能量要较强，以满足充分激励的条件，同时高频区能量要低，从而对高频分量不激励。

PRBS的能量分布与其变换频率相关，通过功率谱密度（Power Spectral Density，PSD）分析能看出变换频率与能量分布的关系，在采样率w分别为1000Hz、500Hz、333Hz的情况下，采集PRBS的变换频率分别为不同采样率w的1，1/2，1/3倍（即分频，1/2倍代表2分频）时的PRBS（位数为8，幅值为0.1），然后进行PSD分析，结果如图4所示。

可以看出，相对于不同采样率的相同分频数，激励信号的能量分布特性一致，不分频时，能量在w范围内均匀分布，2分频时大概在w的0～0.35的范围内能量比较强，剩余区域能量较弱，3分频时会在w/3处有断档。在采样率为参考的基础上，对伪随机信号进行2分频处理。可以使高频能量衰减，对带宽范围所属的低频区激励较多。

对于PRBS的位数和幅值的选择，要结合对象的运动范围考虑。如果PRBS的正负脉宽数量不均匀，惯量盘就会随时间增长向某一方向靠近而撞击到轴挡，而不是在工作点附近来回运动，此实验中待辨识的小型化稳定平台主要是电机驱动负载在俯仰方向内运动，上下有限位的设置，分别在正负85°角的位置处，以防止连续旋转使线绕断裂，所以对象的运动范围也就被限制在其中，图5即为负载分别在俯仰框内0°，45°，85°的示意图。

图5 负载分别在俯仰框内位置0°，45°，85°的示意图

通过测试，由7位和8位PRBS产生的一个周期内的序列里的正负脉宽的数量比较对称。

PRBS信号的序列长度满足下式：

＝2－1(13)

式中：为寄存器数。

除此之外辨识前要进行数据预处理，对I/O数据进行去除对应工作点的直流分量的工作。主要分两步：

1）计算I/O数据的平均值。

2）从I/O数据中减去平均值，得到新的I/O数据。

4 实验验证

搭建数字控制系统进行系统辨识的实验和验证工作。数字系统主要由直流电机、旋转变压器、惯量盘、功率放大器和Dspace数字控制平台组成。图6为以俯仰方向为例的伺服系统控制框图，其中对稳定平台进行伺服控制的功率放大器的电压调制输入信号通过Dspace设备提供，旋转变压器用来测量俯仰轴的转角信息，信号采集解算卡对旋变模拟信号进行采集，按照16位的分辨率进行解算，并按照数据组合据协议进行处理后，由Dspace接收并传输给上位机。

图6 稳定平台的系统控制框图

4.1 交叉实验和白噪化验证

设计交叉实验，用来确定PRBS经过PSD分析后的能量分布对高低频率区间的激励如何分配时，可以使辨识出的参数模型的动态特性更贴近真实系统，然后选取通过白噪化验证的模型进行非参数化验证。其中白噪化，是利用两个信号之间的误差的自相关性来描述他们响应的相似程度，进而反映实际对象与模型的差异大小[7]。如果在时间零点两者的相关值为理想的1，而在不同时间间隔下比对的相关值减小，则表明两者相关性很高，系统响应近似相等。

通过下述的验证准则来判别是否模型有效：

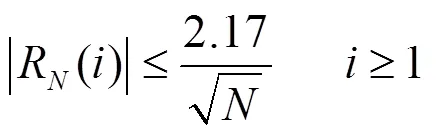
式中：＝200为采样数，交叉实验结果和分析如表1所示。

可以看出：激励信号对系统带宽范围内的频率成分起到激励作用，但是要对带宽以外的部分（～3范围）起到部分激励时，预测模型能够通过验证。太高采样率会引入高频噪声，并且使辨识过程中观测向量T之间的数值条件变差，如果用降低采样率而不经分频处理的PRBS信号激励，在整个0～0.5区域内的能量均匀分布，对此范围内频率成分会均匀激励，高频区也会得到更多激励，对辨识结果有影响，最终未能通过验证根据交叉实验结果，通过白噪化验证的离散化参数模型为：

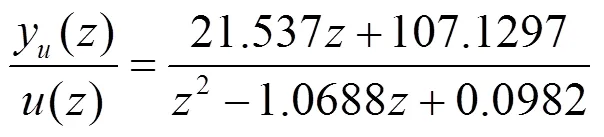
成形滤波器的模型如下：

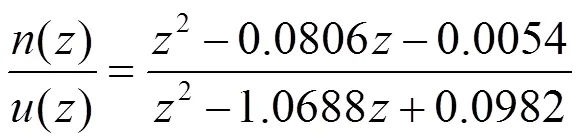
图7展示了辨识过程中，在采样率为3ms时，经2分频处理后的PRBS激励下的速度响应曲线。图8展示了实际系统与通过白噪化验证的参数模型的速度输出响应在200个采样点下的误差曲线。

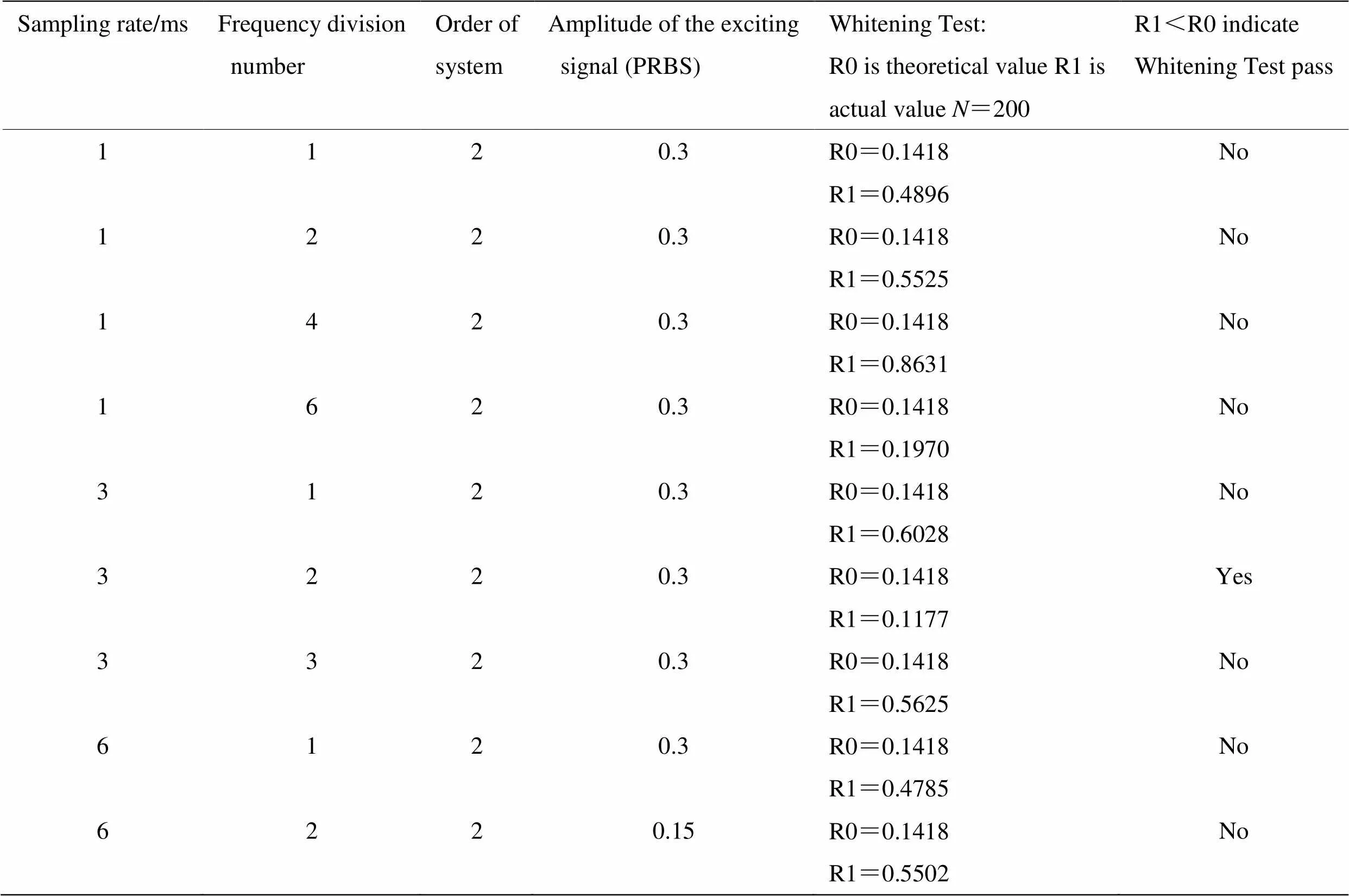
表1 交叉实验结果

图7 系统输出速度响应

图8 模型与系统的输出响应误差

4.2 开环验证

开环验证属于非参数化的验证方法，检验预测模型的输入/输出的特性与实际系统输入/输出特性的吻合程度。在系统带宽和仿真步长的影响下，系统响应对不同的信号会呈现各自不同的特点[8]。

输入信号是直流信号可以验证两者的时不变性，稳态值，动态特性等指标吻合度，但由于系统有限行程的限制，可能会在没有进入稳态前就会停止运动，所以另外考虑选择不同频率正弦信号进行验证，在俯仰方向内来回运动，频率高的信号变化快，一个周期内作用于系统上的电压持续时间低于低频信号作用时的情况，所以频率高的信号使对象运动速度的幅值肯定相对要小。

虽然知道成形滤波器的结构和参数，但是真实系统引入的噪声不可测，仿真时无法直接对模型施加与真实系统内部白噪声特性一致的白噪声，也不能盲目确定其量级和变化情况，否则会对模型真实输出影响很大，在这里只能对比预测模型的理想输出和实际系统真实输出的误差特征，控制率保持3ms不变，幅值都选择0.1时，以阶跃信号作为输入信号激励时，负载在俯仰方向上的实时运动位置如图9，实际运动速度输出与预测模型速度输出对比结果如图10，预测模型的动态响应结果如图11，当分别以5Hz和30Hz正弦信号作为输入信号激励时，实际系统与预测模型的速度输出对比结果依次如下图的12～13，其中表2～3依次为两者在不同正弦信号激励下的动态响应指标对比结果。

图9 阶跃信号作用下负载运动位置响应

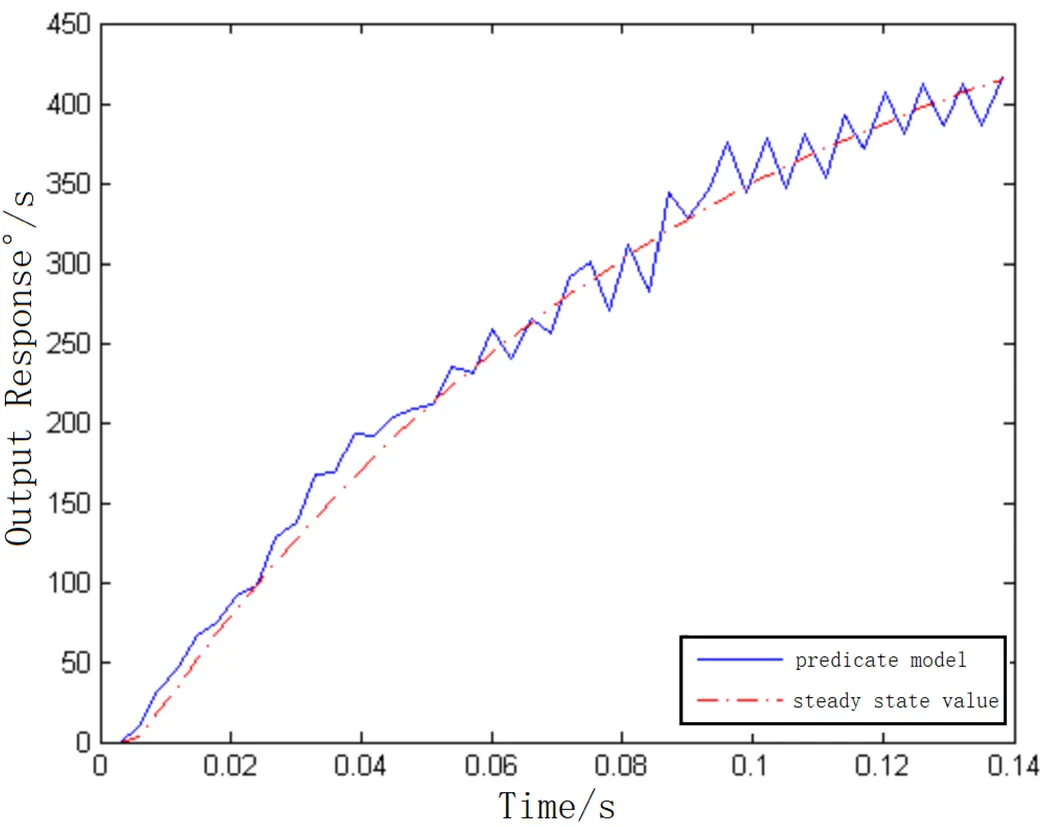
图10 阶跃信号作用下速度变化

图11 阶跃信号作用下预测模型动态响应

图12 5Hz正弦信号激励下输出响应对比

图13 30Hz正弦信号激励下输出响应对比

表2 5Hz正弦信号输入时速度响应参数对比表

表3 30Hz正弦信号输入时速度响应参数对比表

通过图9～11可以看到：在阶跃信号作用下，负载在整个行程范围内，没有进入稳态过程，模型的输出响应要在0.36s以后进入稳态区（2%误差），但是两者在上升过程中的速度曲线贴近，说明前段运动过程中，动态特性基本一致。通过图12～13可以看到：在两种不同频率的正弦信号作用下，模型速度输出响应与系统速度输出响应的周期和幅值偏差都比较小，且系统和模型的动态曲线匹配更好。

5 结论

本文以红外稳定平台伺服系统为研究对象，先对其进行了动力学建模，并通过线性化处理和系统特性理论分析，给出了实验方式下参数辨识的具体步骤并进行了模型有效性的验证。辨识得到的离散化参数模型通过了参数化的白度测试和非参数化的开环验证，可见通过增大输入信号增益使负载运行在高速环境下，并有合理的激励系统带宽范围，确实能够通过实验辨识得到对实际系统刻画比较精确的参数化模型。

[1] 予阳. 美国未来侦察骑兵系统[J]. 兵器知识, 2005(10): 43-45.

YU Yang. Us future reconnaissance cavalry system[J]., 2005(10): 43-45.

[2] 陈苗海. 侦察监视车及其光电传感器的发展现状[J]. 激光与红外, 2005, 33(7): 459-462.

CHEN Miaohai. Development status of reconnaissance and surveillance vehicle and its photoelectric sensor[J]., 2005, 33(7): 459-462.

[3] 朱耘, 韩根甲. 无人机光电探测技术的现状及发展趋势[J].舰船科学技术, 2004, 26(6): 1-5.

ZHU Yun, HAN Genjia. The current situation and development trend of UAV photoelectric detection technology[J]., 2004, 26(6):1-5.

[4] 廖洪波. 光电稳定平台伺服系统动力学建模与参数辨识[D]. 长沙: 国防科技大学, 2008.

LIAO Hongbo. Dynamic modeling and parameter identification of servo system of photoelectric stabilized platform[D]. Changsha: National Defense University of Science and Technology, 2008.

[5] Debruin J. Control Systems or Mobile Satcom Antennas[J]., 2008, 28(1): 87-101.

[6] Guelman M, Kogan A, Kazarian A. Acquisition and Position Control for Inter-satellite Laser Communications[J]., 2004, 40(4): 1239-1249.

[7] Ren Z., Stephens L Laser. Pointing and Tracking using A Completely Electromagnetically Suspended Precision Actuator[J]., 2006, 29(5): 1235-1239.

[8] 毕永利. 多框架光电平台控制技术研究[D]. 长春: 中科院长春光机所, 2003.

BI Yongli. Research on control technology of multi-frame photoelectric platform[D]. Changchun: Changchun Institute of Optics and mechanics, Chinese Academy of Sciences, 2003.

Parameter Identification for Miniature Stabilized Platforms Based on Infrared Imaging

GUO Xuefeng，LIN Yu

(Kunming Institute of Physics, Kunming 650223, China)

This study focuses on parameter identification for miniature stabilized platforms based on infrared imaging and offers a linearization technique to reduce the nonlinear effect on modeling identification. During the identification process, a pseudorandom binary sequence is used as the modulated input signal to drive the system, and the corresponding system output is a velocity signal. In addition, the augmented least square method is applied to identify the discrete modeling parameter. Finally, the precision of the modeling is tested in two ways: parameterization and non-parameterization. The results show that parameter modeling can adequately describe the dynamic character, similar to the real system.

stabilized platform，parameter identification，open-loop identification，augmented least square method

TP273

A

1001-8891(2020)01-0030-10

2019-09-28；

2019-12-31.

郭雪峰（1992-），男，汉族，硕士研究生，研究方向主要以光电稳定平台为主，进行相关伺服控制和系统辨识的研究，E-mail：gxf19921027@163.com。

林宇（1972-），男，云南昆明人，博士，博士生导师，主要研究方向为光电技术，E-mail: lwlinyu@163.com。