基于燃料比最优的高炉喷煤设定值多目标优化

崔桂梅，吕明远

(内蒙古科技大学信息工程学院，包头 014010)

钢铁工业是中国经济发展的基础产业，也是能耗最严重的行业之一。据统计，中国钢铁工业能耗约占全国总能耗的15%，其中高炉炼铁产生的能耗约占其60%[1]。面对钢铁工业节能降耗的严峻形势，高炉炼铁向高效、低耗、自动化方向发展势在必行[2]。高炉喷煤技术是现代高炉炼铁生产广泛采用的技术，已成为高炉下部调节所不可缺少的重要手段之一。以价格低廉的煤粉部分替代价格昂贵且日趋匮乏的焦炭，既降低高炉炼铁的焦比，节约成本，也降低了炼焦生产的能耗与污染。因此，提高喷煤量替代部分焦炭是高炉生产降低能耗、节约成本的有效措施。

高炉运行在不同炉况下有一个相应的最佳喷煤量，但由于高炉炼铁过程存在复杂性、滞后性和状态多变性，喷煤设定值由炉长人为给定，很难准确地决策出当前炉况下的最佳喷煤量。目前，对于喷煤量决策的研究主要以优化模型为主，即利用高炉炼铁过程的历史数据，采用线性规划、GA-BP、模式匹配等方法建立优化模型，决策出高炉炼铁过程的最佳喷煤量[3-5]。这些优化模型对于非线性极强的复杂生产过程而言，存在局部极小，实时性和准确性较差等问题。

在高炉喷煤过程中，提高喷煤量的前提是保证煤粉消化率高，而炉温与煤粉消化能力密切相关，是实时判断炉况的主要依据，因此，对炉温的预测就显得尤为重要。近年来，中外学者采用智能算法对炉温进行了预测，基于数据的预测模型主要有：神经网络[6-7]、多元时间序列[8]、基于Bootstrap的二维预报[9]等。以上研究对炉温预测提供了新思路，但并未将炉温预测与喷煤量决策建立起直接联系。

炼铁燃料比是衡量高炉生产能耗和成本的重要指标之一，主要由煤比和焦比组成，而焦炭价格昂贵，所以实现燃料比最优化应从两方面考虑：第一，降低高炉炼铁的总体燃料比；第二，在总体燃料比一定的情况下，尽可能地提高其中的煤比，降低焦比。因此，实现燃料比最优要降低燃料比，提高煤比。

现从燃料比最优的角度，将过程信息、专家经验与智能模型相结合，首次提出以炉温预测指标作为约束条件的喷煤设定值多目标优化方法，实时、准确地决策出当前炉况下的最佳喷煤设定值，并通过仿真模型验证其有效性。

1 高炉炼铁过程运行优化基本思路

高炉是复杂的强耦合系统，从高炉顶部进行加料到铁水出炉(为一个冶炼周期)及工艺指标检测信息反馈给高炉操作者需要约8 h。高炉冶炼操作控制上部炉顶布料(铁矿石，焦炭)为间歇式控制变量，焦炭从布料进入炉中到燃烧发挥作用需要2/3周期；下部煤粉喷吹与高温热风输入为连续式控制变量，煤粉从喷入风口到燃烧发挥作用需要1/3周期。上部控制的物料成分和料速相对稳定，仅在炉况波动时调整，而下部在最高风温和风量下，通过调节喷煤量来快速调整炉温。

依据这种上部长机制、下部短机制操作模式的特点，利用分层优化方法，将高炉运行优化控制问题等效为有约束的上部、下部子系统优化控制问题。高炉平稳运行时，因上部布料控制相对稳定，对下部炉温控制的影响等效为慢干扰，在上部与下部解耦的基础上，进而单独研究高炉下部的喷煤优化控制问题。

目前，高炉冶炼下部喷煤操作仍采用人工模式，即操作人员根据工艺指标及冶炼知识，凭借积累的经验决策出喷煤设定值，并根据炉温、炉况对喷煤量进行增减操作。但由于高炉冶炼过程存在复杂性、滞后性和状态多变性，喷煤设定值由炉长人为给定，存在盲目性，粗糙性等问题，无法准确地决策出当前炉况下的最佳喷煤设定值。

综上所述，提出基于燃料比最优的高炉喷煤设定值多目标优化方案。利用高炉炼铁的海量生产数据，首先，采用基于K-均值聚类的径向基神经网络建立优化目标关联模型；其次，采用基于时间序列的径向基神经网络建立炉温预测模型；最后，以优化目标关联模型为目标函数，炉温预测指标为约束条件，喷煤量为决策变量，建立多目标优化模型，并通过基于NSGA-Ⅱ算法的多目标优化方法来优化决策喷煤设定值，其运行优化控制框图如图1所示。

图1 运行优化控制框图

2 数据预处理

以某钢厂2 200 m3高炉为研究对象，采集了近6个月的生产数据。由于高炉炼铁生产过程中生产边界条件变化及外界干扰的影响，使得实际过程数据存在异常值；由于数据采集过程中受到检测装置，人为因素与现场环境等诸多因素的影响，使得部分采样数据中存在缺失值。需要通过数据预处理来得到合格的建模数据，提高建模准确性。

2.1 变量选取

采用500组生产数据作为研究数据，结合其生产现状与专家经验确立优化目标，确定对优化目标(燃料比、煤比)及炉温指标(铁水温度、铁水硅含量)有影响的因素主要为料速、风量、热风压力、炉顶压、压差、透气性、热风温度、富氧率、喷煤量、顶温高、顶温低、水温差、煤气利用率、焦炭量及上一炉铁水温度、硅含量、锰含量、磷含量、硫含量。以上述19个变量作为输入变量，以料燃比、煤比、铁水温度和铁水硅含量4个变量作为输出变量，一共选取23个变量进行数据预处理。

2.2 异常值检测与修补

当高炉平稳运行时，采集的过程参数应该在小范围内波动，不会出现异常值。依据3σ准则，异常值被定义为样本数据与其平均值的偏差大于3σ的数据。经3σ准则，将原始样本集中检测出的异常数据赋空值，得到中间样本集。之后，对上述空值和因检测设备或人为因素造成的缺失值，用前后四组数据通过拉格朗日插值法进行数据修补。

(1)

式(1)中：μ和σ分别为样本数据的平均值和标准差。

2.3 相关性分析

在建立模型时，过多的输入变量会增加模型的复杂度和计算时间，因此需要对建模数据进行降维。相关性分析是数据降维的常用方法，是用来分析变量间直线相关程度的一种广泛使用的统计学方法。假设有两组观测值，X:x1,x2, …,xn，Y:y1,y2, …,yn，记ρXY为X与Y的相关系数，取值为[-1,1]，其计算公式为

(2)

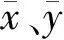
对采集的500组高炉生产过程数据进行相关性分析，分别计算19个输入变量与4个输出变量的相关系数，结果如表1所示。根据计算结果，选择相关系数|ρXY|≥0.1的变量作为关键输入变量。最终确定燃料比、煤比关联模型的输入变量个数分别为5个和7个，铁水温度和铁水硅含量预测模型的输入变量的个数分别为6个和11个。

表1 相关性分析结果

3 优化模型建立

3.1 基于K-均值聚类的径向基神经网络

径向基神经网络(RBF网络)是由三层构成的前向神经网络，具有结构简单、训练速度快、全局收敛等特点，对非线性函数有着良好的逼近能力[10]。RBF网络的隐含层是非线性的，采用径向基函数作为基函数，从而将输入层向量空间转换到隐含层空间，使原来线性不可分的问题变得线性可分，而输出层则是线性的，其网络结构如图2所示。

图2 RBF网络结构图

RBF网络隐含层的基函数一般采用高斯函数，其表达式为

(3)

RBF网络的输出为

(4)

式(4)中：ωij和bj分别为输出层的权值和阈值。

根据径向基函数中心确定方法的不同，RBF网络有不同的学习策略。此处采用的学习策略为自组织选取法，通过K-均值聚类的方法求解基函数的中心。K-均值聚类算法可以将数据点划分为几大类，因为同一类型数据点内部有相似的特点与性质，从而使选取的中心点更有代表性。自组织学习选取法计算步骤如下。

(1)网络初始化。随机选取h个训练样本为聚类中心ci(i=1,2,…,h)。

(2)将输入的训练样本集合按最邻近规则分组。按照Xp与中心ci之间的欧氏距离将Xp分配到输入样本的各个聚类集合中。

(3)重新调整聚类中心。计算各个聚类集合中训练样本的平均值，即新的聚类中心ci，如果新的聚类中心不再发生变化，则得到的ci即为最终的基函数中心，否则返回(1)，进入下一轮的中心求解。

(4)求解方差σi。该网络的基函数为高斯函数，因此方差σi可由式(5)求解。

(5)

式(5)中：cmax为所选取中心之间的最大距离。

(5)计算隐含层和输出层之间的权值。隐含层至输出层之间的连接权值可以用最小二乘法直接计算得到，计算公式为

i=1,2,…,h

(6)

3.2 优化目标关联模型

多目标优化的优化目标为燃料比最优，即降低燃料比，提高煤比。因此，采用基于K-均值聚类的径向基神经网络分别建立燃料比，煤比与喷煤量的关联模型。

采用数据预处理后的500组优良数据，其中400组作为训练数据，100组作为测试数据。根据相关性分析结果，选取喷煤量、料速、风量、炉顶压、焦炭量，5个变量作为模型的输入变量，燃料比作为输出变量，建立燃料比关联模型；选取喷煤量、焦炭量、料速、压差、炉顶压、富氧率、煤气利用率，7个变量作为模型的输入变量，煤比作为输出变量，建立煤比关联模型。经过参数寻优，当选取聚类中心个数分别为21、20个时，燃料比、煤比关联模型精度较好，其预测结果和误差曲线如图3所示。通过MATLAB训练的RBF网络模型为

(7)

式(7)中：f1为燃料比；f2为煤比。

图3 优化目标关联模型

3.3 炉温预测模型

多目标优化的约束条件为炉温预测指标，铁水温度表征高炉的物理温度，铁水硅含量表征高炉的化学温度，因高温作业和复杂的炉内环境，二者很难实时测得，只能出铁后进行检测，具有滞后性。因此，采用基于时间序列的径向基神经网络分别建立铁水温度、铁水硅含量预测模型。

根据相关性分析结果，选取喷煤量、压差、上一炉次铁水温度、硅含量、磷含量、硫含量，6个变量为模型的输入变量，建立铁水温度预测模型；选取喷煤量、热风温度、风量、富氧率、料速、透气性、炉顶压、上一炉硅含量、磷含量、铁水温度、锰含量，11个变量为模型的输入变量，建立铁水硅含量预测模型。经过参数寻优，当选取聚类中心个数分别为22、36时，铁水温度、铁水硅含量预测模型精度较好，其预测结果和误差曲线如图4所示。通过MATLAB训练的RBF网络模型为

图4 炉温预测模型

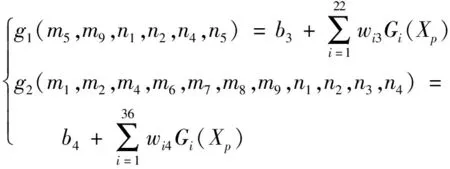
(8)

式(8)中：g1为铁水温度；g2为铁水硅含量。

3.4 模型评价

传统的神经网络预测模型的性能评价指标主要考虑平均相对误差(MRE)和命中率(HR)，其计算公式为

(9)

(10)

(11)

依据专家经验：d1=15 kg/t，d2=7.5 kg/t，d3=15 ℃，d4=0.1%，因此各模型的性能评价指标如表2所示。

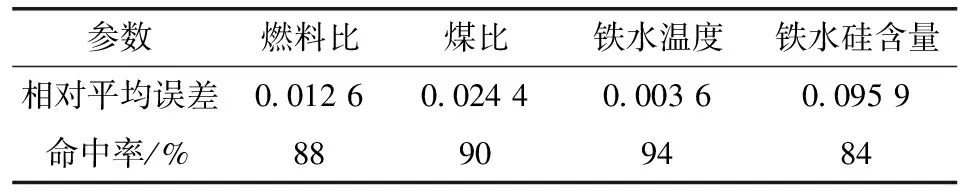
表2 各模型的性能评价指标

4 基于NSGA-Ⅱ算法的多目标优化

4.1 NSGA-Ⅱ算法原理

NSGA-Ⅱ算法是在NSGA算法的基础上，增加了非支配排序和拥挤度计算环节,并引入精英保留策略，在形成新父代种群之前，将旧父代和子代合为一体并进行非支配排序和拥挤度计算。运用这种方式，不仅能够保留旧父代中的精英解，而且扩大了个体的采样空间[11]，其算法流程如图5所示，具体计算步骤如下：

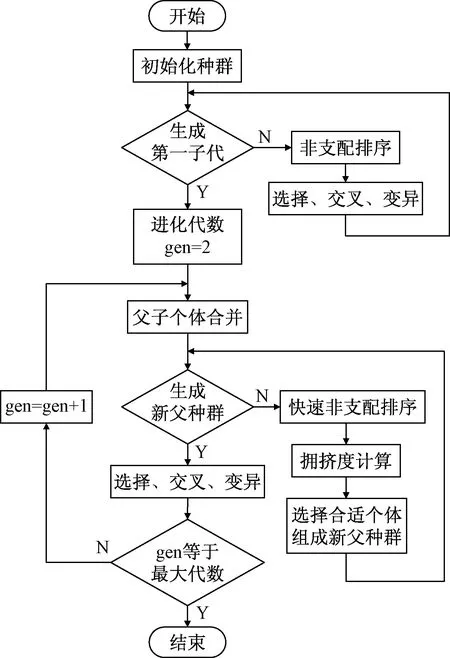
图5 NSGA-Ⅱ算法流程图

(1)随机产生包含N个个体的初始种群(该过程与普通遗传算法相同)。

(2)判断是否生成第一子代，如果否，则进行非支配排序和选择、交叉、变异等遗传操作，再进行判断。

(3)置遗传代数计数器gen=2。

(4)合并父代、子代种群，形成一个中间种群，规模约为2N。

(5)判断是否生成新父种群，如果否，则进行快速非支配排序和拥挤度计算，选择合适个体组成新父种群，规模为N，再进行判断。

(6)进行交叉、变异等遗传操作，产生新子代种群。

(7)若gen小于最大代数，返回(4)；否则结束。

4.2 多目标优化及其结果

在多目标优化问题中，各目标之间是相互冲突、相互制约的，在使得一个优化目标性能改善的同时往往是以损失其他目标的性能为代价的。因此，不可能存在一个使所有目标性能都达到最优的解。所以多目标优化问题的解通常为非劣解，即Pareto最优解。其解通常不是唯一的，而是由多个解构成的Pareto最优解集，解集中任何一解均可成为最优解，这取决于设计者的意愿和对各目标的重视程度。多目标优化算法的目的就是要寻找Pareto最优解集。

采用基于NSGA-Ⅱ算法的多目标优化算法求解，在满足约束条件下，能使优化目标尽可能同时达到最优的Pareto最优解。依据专家经验，铁水温度1 490～1 510 ℃为良好，铁水硅含量0.45%～0.55%为良好，喷煤量的上下限约束为35～45 t/h，因此其多目标优化模型为

minf1(m1,m2,m4,m9,m14)

maxf2(m1,m4,m5,m8,m9,m13,m14)

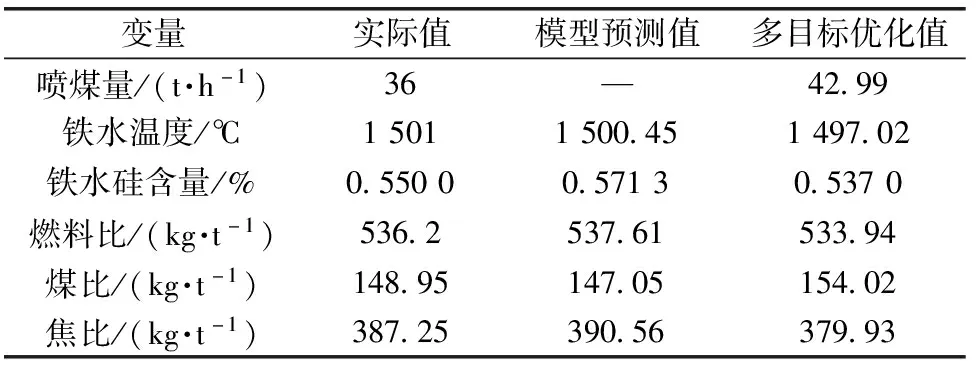
s.t. 1 490

0.45

n3,n4)<0.55

35

(12)

在优化过程中决策变量仅为喷煤量，其他输入变量均取当前检测值[12],分别为料速5 批/h，风量5 026 m3/min，炉顶压0.209 MPa，压差0.161 MPa，透气性31.1 m3/(min·kPa)，热风温度1 134 ℃，富氧率2.23%，喷煤量36 t/h，煤气利用率47.96%，焦炭量93.76 t/h，及上一炉次铁水温度1 500 ℃、硅含量0.54%、锰含量0.54%、磷含量0.151%、硫含量0.032%。为将目标函数统一为求最小值，将f2变换为-f2，则多目标优化模型可转换为

minf1(m9)

min-f2(m9)

s.t.1 490

0.45

35

(13)

用NSGA-Ⅱ算法求解决策变量的Pareto最优解，设置种群数量为100，最优前沿个体系数为0.5，最大进化代数为100，通过优化获得的Pareto最优前沿曲线如图6所示。

图6 Pareto最优前沿曲线

由图6知，Pareto曲线两端的解只能令其中一个优化目标较好，而另一个目标则较差，左端的点f1(燃料比)较好，但f2(煤比)较差，而右端的点则相反。依据专家经验，应优先考虑第一个优化目标f1，即在保证燃料比降低最多的前提下，煤比尽量提升即可。因此取Pareto曲线左端的10个点作为Pareto最优解集，从MATLAB中导出这10个解及其相对应的优化目标和炉温指标，如表3所示。

表3 Pareto最优解及其优化目标和炉温指标

表3中的Pareto最优解所对应的炉温预测值良好，且燃料比和煤比均有所改善。其中，第1个Pareto最优解对应的燃料比降低最多，煤比也提高较多。因此将第1个解作为最佳喷煤设定值，即42.99 t/h。通过该优化方案求解出了与当前炉况相适应的最佳喷煤设定值，及其对应的铁水温度，铁水硅含量，燃料比，煤比，并可计算出焦比(燃料比减去煤比)，其优化结果对比如表4所示。

表4 优化结果对比

由表4可知，模型预测值与实际值接近，表明了预测的准确性较高。经多目标优化后，炉温指标仍处于良好范围内，喷煤量提高了6.99 t/h，燃料比降低了2.26 kg/t，煤比提高了5.07 kg/t，实现了降低燃料比，提高煤比的优化目标。同时，焦比降低了7.32 kg/t，减少了对焦炭的需求，降低了炼焦生产的能耗和污染。以当前煤粉和焦炭的市价计算(煤粉960元/吨，焦炭2 010元/吨)，吨铁可节约成本9.85元，以每天生产约6 000 t生铁计算，每天可节约成本约59 100元。

5 结论

根据某钢厂2 200 m3高炉的生产现状及专家经验，确定了与喷煤量相关的优化目标和约束条件。采集近6个月的生产数据，并对数据进行预处理。采用基于K-均值聚类的径向基神经网络建立优化目标与喷煤量的关联模型，采用基于时间序列的径向基神经网络建立炉温预测模型，并验证了模型的准确性。以优化目标关联模型为目标函数，炉温预测指标为约束条件，喷煤量为决策变量，建立多目标优化模型，并采用基于NSGA-Ⅱ算法的多目标优化方法进行优化求解，获得了当前炉况下的最佳喷煤设定值。结果表明，该设定值可以在保证炉温良好的前提下使燃料比达到最优，达到了提高喷煤量，降低能耗，节约成本的目的。该优化方案不仅为高炉实际生产提供了操作指导，也为高炉冶炼的优化运行奠定了良好的基础。