关节式双履带移动机器人越障稳定性分析

宗成国，刘纪新，于 岩，徐丕兵

(1.青岛黄海学院智能制造学院，青岛 266427；2.山东科技大学机械电子工程学院青岛 266510；3.青岛市技师学院轨道交通学院, 青岛 266229)

履带式移动机器人作为一种对非结构环境探索的智能化设备，可以辅助工作人员对非结构环境进行远距离的侦测与探查工作，降低事故的发生率[1-2]。

目前，国内外研究学者在履带式移动机器人相关领域做了大量研究工作。美国在该领域的研究走在了世界的前列，IRobot公司研制的Packbot机器人是一种用于城市建筑物救援的微小型履带式移动机器人，该机器人前端安装两摆臂，可有效提高机器人的越障能力[3]；德国Telerob公司研制的Teodor机器人是一款用于排爆的履带式移动机器人，该机器人已多次应用于反恐演习中[4]。中国也在开展履带式移动机器人的研究工作，哈尔滨工业大学研制了一种用于煤矿井下探测的六履带移动机器人，该机器人可对井下巷道的环境进行检测[5]；北京航空航天大学研制了一种可重组的履带式移动机器人，该机器人具有较强的爬楼梯能力[6]。

以上所提及的履带式移动机器人可分为双履带移动机器人、四履带移动机器人、六履带移动机器人三种[7-9]。双履带移动机器人的特点是结构简洁紧凑，可实现轻量化，但与四履带移动机器人和六履带移动机器人相比，其越障稳定性较差。因此，如何保证双履带移动机器人既具有较强的越障稳定性能，又结构简洁紧凑，则是履带式移动机器人领域急需解决的一个热点和难点问题[10-14]。

拟设计一种基于非结构环境的关节式双履带移动机器人，该机器人平台可由前、后壳体组成，在旋转关节的作用下，该机器人将实现同四履带机器人一样跨越障碍物；此外，由于履带的周长是固定不变的，此状态下机器人的履带会变松，容易引起打滑或脱落，为解决这一问题，提出一种履带压紧装置，该装置可实现机器人在工作中根据履带形状伺服压紧履带。在此研究基础上，将以攀越二维崎岖地形、正斜坡地形以及楼梯三种典型地形为例，对关节式双履带移动机器人的越障稳定性能进行相应的分析。最后，通过相关实验来证明关节式双履带移动机器人的机构设计合理性和可行性。

1 机器人整体结构设计

履带式移动机器人适合在复杂地形的环境下进行作业。这类机器人除进行正常形式的前向、后向和旋转的基本动作外，还要具备攀越障碍物及攀爬楼梯的能力。所以，履带移动机器人在非结构化环境下的运动稳定性的提高是机器人实现自身稳定运行的前提和保证。

结合上述分析，一种基于探索非结构环境的关节式双履带移动机器人便应运而生了，该机器人平台由前壳体、后壳体、两条履带、六个履带轮、一个关节电机、两个驱动电机、两套履带压紧装置、一套无线通信装置和一套电路控制系统组成，如图1所示。后壳体的尾部位置安装有两驱动电机；前、后两壳体相接触的位置安装有用于调整机器人姿态的关节电机，控制系统会根据传感器所检测到的信息控制前壳体绕关节轴旋转相应的角度，机器人便可顺利实现越障或攀爬楼梯。机器人平台的后壳体内安装有控制系统以及蓄电池，前壳体内安装有无线通信装置。

图1 机器人总体机构示意图

2 机器人越障稳定性分析

2.1 二维崎岖地形的越障稳定性分析

如果机器人在水平面行驶的过程中碰到小石头或经过凹凸不平的地面时，前壳体部分通过关节式电机驱动，可以绕关节轴抬升相应的角度，在这种情况下，机器人的前、后壳体会有某种角度的形成，这便增强了机器人翻越障碍物的性能。这时机器人整机的质心状态如图2所示，通过建立XCY坐标系，以机器人整机后壳体的质心C为原点，以X轴作为水平线，Y轴为其水平线经过坐标原点法线的方向，以D点作为机器人整机的前壳体部分的质心，当机器人整体在运动的过程中，质心Z坐标处于恒定状态，即Lz≡0。利用其质心坐标的公式Z(Gx,Gy)能够推算出机器人整机质心坐标如下：

(1)

式(1)中：α为前壳体部分的摆角；m1为后壳体部分的质量；m2为前壳体部分的质量；L1为后壳体部分长度；L2为前壳体部分长度。

图2 二维复杂地形的机器人结构的质心状态

取机器人整体的前、后壳体部分的质心点，假定全部处于其各自的几何的中心位置，令机器人整体的质量m=m1+m2，式(1)可作如下变换:

(2)

通过上述分析可得，当前壳体部分的摆角α发生变化时，机器人的质心波动的范围是以[m2L1/(2m),0]为圆心，m2L2/(2m)作为其半径的圆上。通过式(2)得知，当其满足刚性条件时，若减小m2/m的值和前壳体部分的质心半径L2/2，可以让机器人整体的质心波动得到进一步减小，提高机器人整体在翻越二维复杂地形时的静态特性。

当机器人翻越障碍物时，前壳体部分的摆角α的摆动范围设置为(-π/4,π/4)，可以得到质心Z(Gx,Gy)的波动范围如下：

(3)

(4)

提出的双履带关节式可动式机器人整体的质量结构数据为：m1=20 kg，m2=8 kg，L1=450 mm，L2=200 mm，α∈(-π/4,π/4)。图3显示了机器人整机的质心坐标Gx、Gy随着前壳体部分的摆角α变化的状态分布。通过图3(a)可知，当α∈(-π/4,π/4)时，机器人整体的质心横坐标可以取到其最大值，当α∈(-π/4,π/4)或α∈(-π/4,π/4)时，质心的横坐标部分可以取得其最小值，在α∈(-π/4,π/4)变化范围内，质心的横坐标变化的曲线取作抛物线。通过图3(b)可知，当α=-π/4时，机器人的质心纵坐标可以取得其最小值部分，当α=π/4时，质心的纵坐标可以取得其最大值，在α∈(-π/4,π/4)变化范围内，质心的纵坐标和前壳体部分的摆角呈现出线性变化的关系，前壳体部分的摆角相对于质心的纵坐标部分影响偏大。

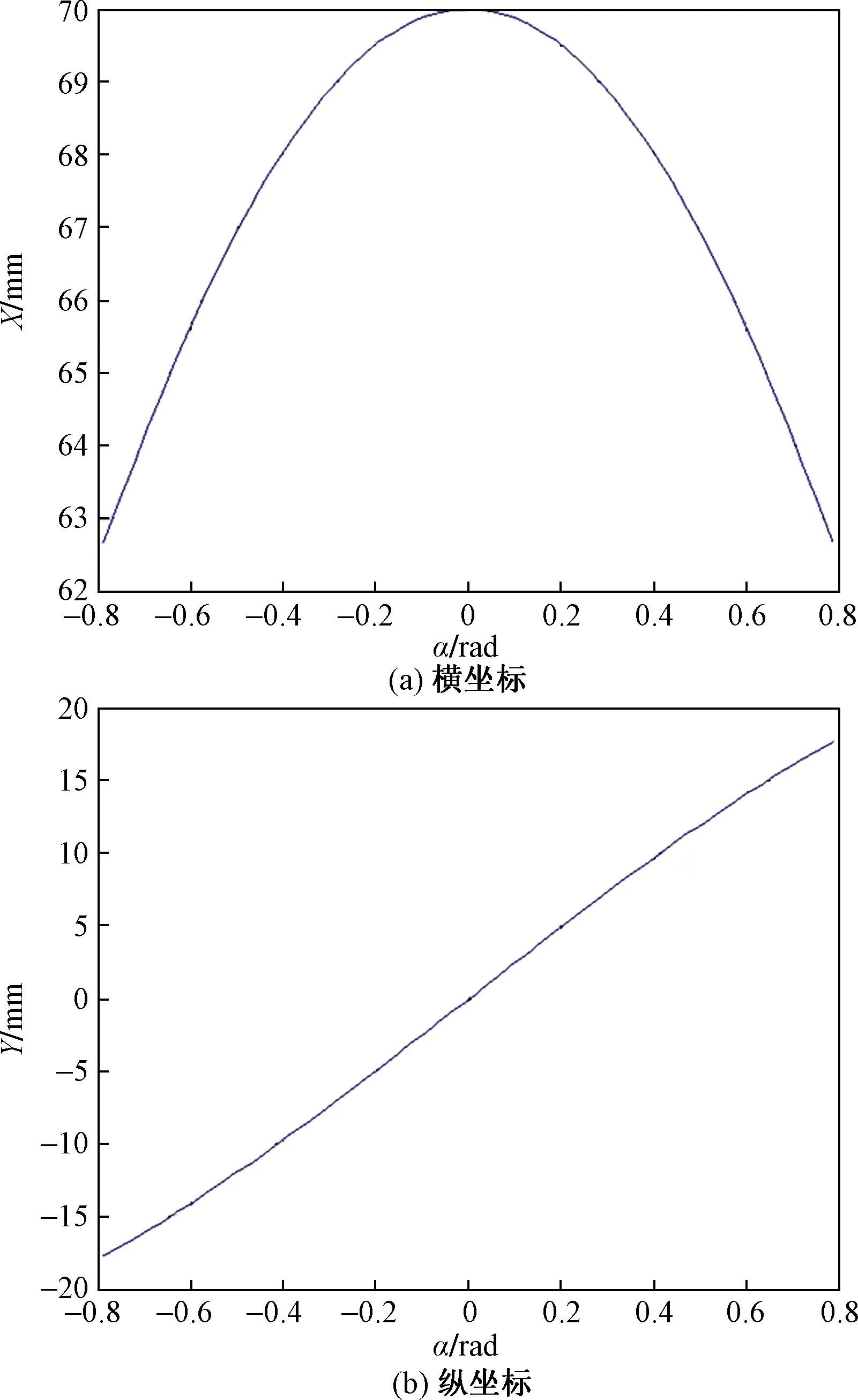
图3 质心的横纵坐标随m1=20 kg变化的分布

2.2 正斜坡的越障稳定性分析

当机器人在正斜坡的地形上动作时，机器人会绕着Y轴进行旋转某β角，如图4所示，如果斜坡面上没有各类阻碍机器人运动的物体，则机器人整机在这种地形上动作时，可以将质心的Z坐标认定为恒定不变，即G′z≡0。通过质心坐标的公式可以得到机器人平台的质心Z(G′x,G′y)的坐标为

(5)

式(5)中：β为斜坡坡度，令m=m1+m2，式(3)可变换为

(6)

当机器人攀越正斜坡时，前壳体部分摆角α的波动范围设置为(0,π/4)，由此可得质心Z(G′x,G′y)的波动范围为

(7)

G′y∈[0,m2L2/(2m)]

(8)

图4 机器人攀越正斜坡地形

图5 质心的横纵坐标随α、β的分布

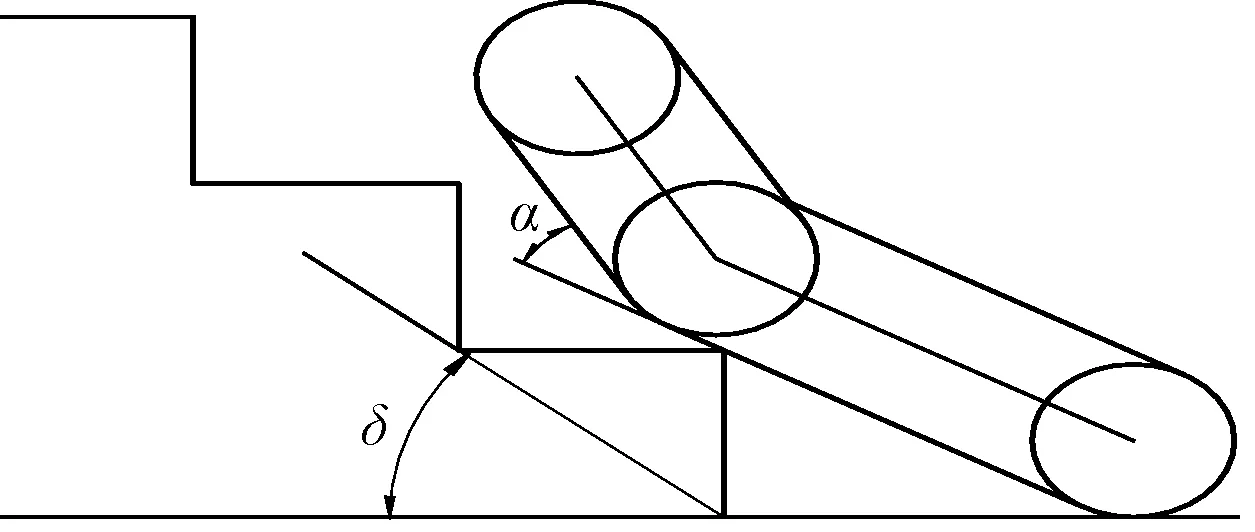
图6 机器人攀越楼梯发生侧翻临界状态

图5所示为机器人整体的质心的坐标G′x、G′y随着前壳体部分的摆角α、斜坡角β波动的状态分布。可知，如果前壳体部分的摆角α∈(0,π/4)，并且当斜坡角β∈(0,π/4)时，质心的横坐标G′x的波动比较小，质心的纵坐标G′y波动则偏大，可以减小m2/m和前壳体部分的质心旋转的半径L2/2，来改善机器人整体在斜坡上运行的稳定特性。

2.3 攀越楼梯台阶的越障稳定性分析

当机器人在爬楼梯台阶的过程中，开始阶段容易产生侧翻，如图6所示，若机器人在位于产生侧翻的临界点时，其后壳体部分和楼梯台阶的边缘接触的地方所产生的支反力是0，在这种情况下，机器人会和与地面碰撞的履带轮的支撑线为轴线产生侧翻，由图6所示的关系得出，机器人产生侧翻时的与楼梯台阶的坡角δ为

(9)

把式(1)代入式(7)，得出：

(10)

结合式(8)，可知机器人整体运动时在刚刚爬楼梯台阶时产生失去稳定性而发生侧翻的表达式为

(11)

通过上述分析，如果要让机器人整体在翻越楼梯的过程中不发生侧翻，必须保证F(α,δ)<0，因此有必要减小前壳体部分的重量在机器人整体的重量中所占的比重，也就是m2/m的比值，和前壳体部分的质心旋转半径L2/2，加大后壳体部分的长度L1。

3 实验分析

为了证实上述所设计的机器人整体的运动学模型分析理论的可靠性，履带式机器人在楼梯台阶、正斜坡以及二维复杂地形上的静态稳定特性以及越障性能的可行性，以设计的双履带关节式可动式机器人作为实验平台，以攀越楼梯为例开展机器人的越障实验。通过爬楼梯越障实验来证明双履带关节式可动式机器人复杂地形的通过性、攀越障碍的可靠性和理论研究的正确性。

图7 机器人翻越楼梯实验

通过图7实验表明，机器人跨越障碍的稳定性能比较好，结构具有紧凑性，便于携带及使用，以及被动调节装置具有非常好的压带功效。

4 结论

(1)设计的关节式双履带移动机器人具备较高攀越障碍的能力，通过实验证明，该机器人具备较强的环境适应性和越障性能。

(2)对机器人攀越二维崎岖地形、正斜坡，以及攀爬楼梯的越障稳定性进行了理论分析，建立了数学模型，实验验证了机器人在越障时具有较高的稳定性。

(3)对机器人攀越障碍的稳定性进行了理论分析，通过实验证明了理论分析的正确性，为研究探索非结构环境机器人提供了参考依据。