Nested 阵列宽带LFM 信号二维DOA 估计
2020-05-24李小琳张文俊
李小琳,张文俊
(1. 上海大学通信与信息工程学院, 上海 200444; 2. 上海机电工程研究所, 上海 201109)
为了确保波达方向(direction of arrival, DOA)估计的精度,阵列相邻天线间距一般要求不大于入射信号的半波长,而当工作频率较高时,相应波长变短,这就要求阵列天线间距变小, 进而导致天线间的互耦效应。为了实现高分辨率,阵列必须具有较大的天线孔径, 这就需要大量的天线来保证。为了节约成本并确保阵列性能,稀疏阵列应运而生。常见的稀疏阵列主要包括最小冗余阵列[1]、Nested(嵌套)阵列[2-4]、互质阵列[5]和分布式阵列[6]等。最小冗余阵列是最早出现的一种稀疏阵列形式,但结构设计复杂。2010 年,Pal 等[2]在最小冗余阵列研究的基础上,提出了一种新颖的稀疏阵列结构,即Nested 阵列。
随着雷达与通讯技术的发展,调制类宽带(linear frequency modulation, LFM)信号以其承载信息量大、抗干扰能力强等优势,得到了愈来愈广泛的应用。但由于宽带信号的阵列流型与频率有关,原有的DOA 估计经典算法已经无法直接应用于Nested 阵列进行宽带信号测角。针对Nested 阵列高精度DOA 测角,Pal 等[2]基于二阶Nested 阵列提出了类似空间平滑(spatial smoothing) MUSIC 算法,但该算法仅可有效估计欠定窄带平稳信号的DOA。张晓凤等[7]和Huang 等[8]提出了基于矩阵重构的ESPRIT 算法,该算法虽不需要求出信号子空间,但仍需进行参数配对。在空间平滑算法的基础上,Coventry 等[9]结合多项式矩阵,实现了互质或Nested 等稀疏阵列的宽带信号空间角度估计,但在空间平滑这一步骤上,该算法性能有待进一步提高。Shi 等[10]通过构造参数化字典,利用联合稀疏结构,提出了一种联合估计稀疏信号和优化参数化字典的迭代最小化方法,解决了Nested 阵列对宽带信号进行欠定到达方向估计的问题,该方法虽然有效,但未提及是否可以实现二维测角。
针对宽带信号测角难题,一种有效的方法是通过聚焦将各频率点上的观测数据在某一子域上对齐,得到聚焦合成的观测量,依此进行宽带LFM 信号的DOA 估计[11]。分数阶傅里叶变换是一种有效的时频域分析工具[12],而时频分析是处理非平稳信号的一种重要方法。作为一种典型的非平稳信号,LFM 信号在分数阶傅里叶域上分别呈现能量聚集性和解线调等特性,这就使得利用FrFT 旋转时频域的特性对宽带LFM 信号进行DOA 估计有了理论依据。为此,本工作基于分数阶傅里叶变换,结合DOA 矩阵方法[13-14],提出一种Nested 阵列宽带LFM 信号二维空间测角算法,实现了对非平稳宽带LFM 信号的空间角度精确估计。
1 算法理论依据
1.1 Nested 阵列原理
Nested 阵列是一种天线布置在规则栅格上的稀疏阵列,一般由两个或多个阵元间距不同的均匀线阵嵌套而成。相对于相同天线数的传统均匀阵列,Nested 阵列具有更大的阵列孔径和更多的自由度,因而具有更高的测角精度与分辨率。下面以常见的二阶Nested 线阵列为例,说明Nested 阵列的结构和特性。二阶Nested 线阵列通常是由两个相邻的均匀线阵嵌套组成:第一级(内层)均匀线阵有L1个天线, 天线间距为d;第二级(外层)均匀线阵有L2=L-L1个天线,其天线间距为D=(L1+1)d。图1 为天线总数为L的二阶Nested 线阵列的结构示意图。

图1 二阶Nested 线阵列结构示意图Fig.1 Structural diagram of 2-level Nested linear array
对于一个有L=L1+L2个天线的二阶Nested 线阵列,其差分协同阵列可以生成2L2(L1+1)-1 个虚拟天线[2],此虚拟阵为均匀线阵,天线位置为

式中,K=L2(L1+1)-1。虚拟阵列的阵元分布如图2 所示。一个有L=L1+L2个天线的二阶Nested 线阵列可以获得2L2(L1+1)-1个自由度。
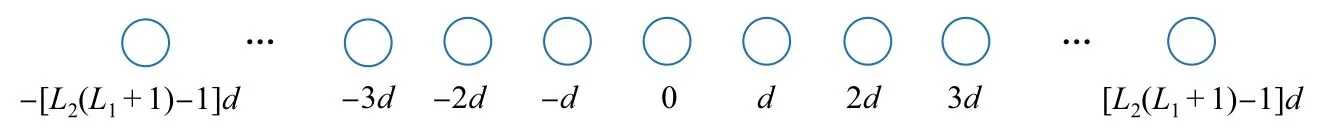
图2 虚拟阵列的阵元分布Fig.2 Elements distribution of virtual array
多阶Nested 阵列可以认为是二阶Nested 线阵列的扩展。对M阶Nested 阵列,每阶阵列的天线数分别为L1,L2,··· ,LM ∈N+,天线位置分布为[2-3]

式中:

M阶Nested 阵列的总物理天线个数为,对应的自由度(degree of freedom,DoF)为
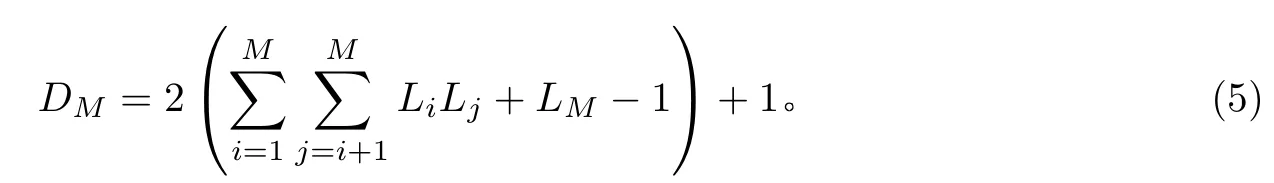
1.2 分数阶傅里叶变换
作为普通Fourier 变换的扩展,分数阶傅里叶变换(fractional Fourier transform,FrFT)非常适于处理瞬时频率特性呈线性变化的LFM 类信号. 图3 为FrFT 示意图。可以看出:如果信号的傅里叶变换可看成将其由时间t轴上逆时针旋转π/2 后到频率f轴上的表示,则FrFT可以看成是将信号在时间t轴上逆时针旋转α角度到u轴上的射线表示[15]。
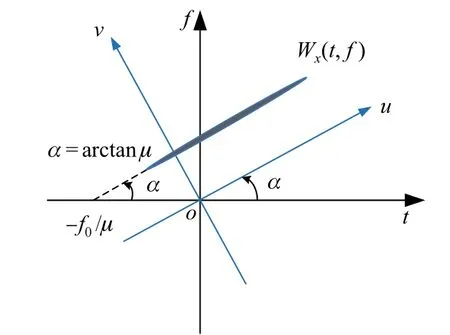
图3 分数阶傅里叶变换示意图Fig.3 Diagram of fractional Fourier transform
信号x(t)的FrFT 定义为
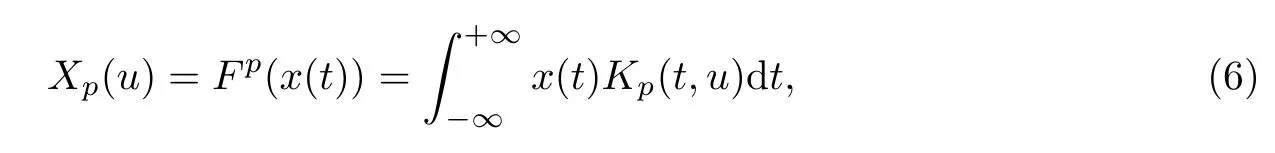
式中:p为FrFT 的阶数,周期为4;u=tanα=tan(pπ);Kp(t,u)为FrFT 的变换核。根据定义可知,FrFT 的逆变换为角度α=-pπ/2 的FrFT,即

如图3 所示,通过旋转坐标轴,会出现两个特殊的分数阶傅里叶域。这两个分数阶傅里叶域分别定义为LFM 信号的解线调域和能量聚集域[12,16-17],相应的FrFT 变换角度分别为

根据式FrFT 变换公式,宽带LFM 信号的FrFT 为
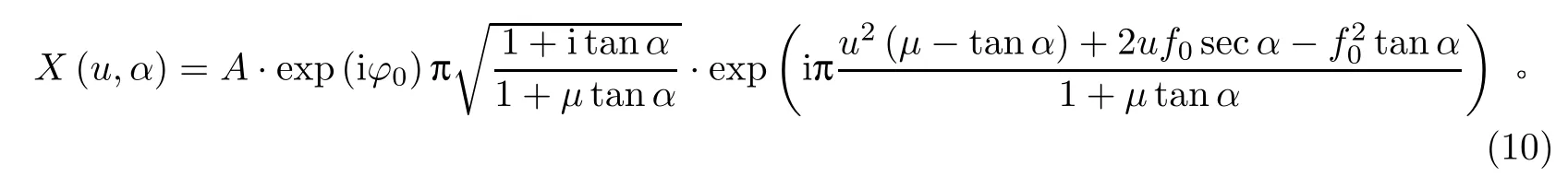
将LFM 信号的解线调域FrFT 变换角度代入上式并化简,得
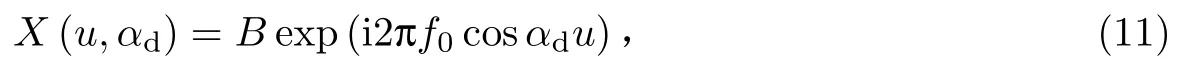
式中,是一个常值。
由式(11)可知,一个宽带线性调频信号解线调域分数阶傅里叶域变换后,该信号被解调为一个单频信号,频率为

由FrFT 的旋转可加特性,可得

即LFM 信号的解线调域和能量聚集域之间存在一个傅里叶变换的关系[18]。
2 宽带LFM 信号模型
假定有K个宽带LFM 信号入射至非均匀平行阵列,信源与平行Nested 阵列的几何关系如图4 所示。非均匀平行阵列由两个子阵列组成,每个子阵列是一个二阶Nested 线阵列。第一个子阵列沿y轴展开,第二个子阵列沿x轴平移距离dx展开。第k个宽带LFM 信号sk(t)的方位角和俯仰角分别为φk和θk,且φk ∈[0,],θk=[0,/2]。

图4 信源与平行Nested 阵列几何示意图Fig.4 Geometric sketch of sources and parallel Nested array
每个子阵列包含L个天线,它们被放置在一个二阶线性嵌套阵列结构中。线性Nested 子阵列由两个级联的均匀线阵(uniform linear array, ULA)组成(见图5),其中第一个ULA 包含间隔为dy的L1个天线,第二个ULA 包含间距为Dy= (L1+1)dy的L2=L-L2个天线。假设p为包含天线y轴坐标的L×1维向量,则有p=(0,1,L,L1-1,L1,2L1,L,L2L1)dy.
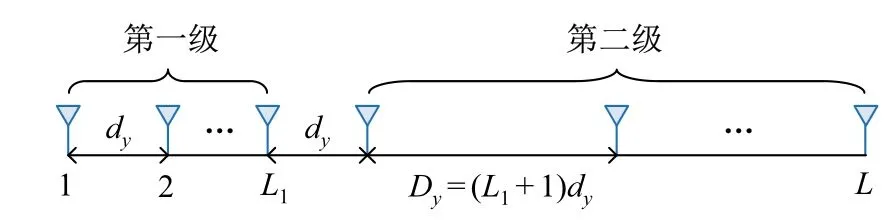
图5 Nested 子阵列天线阵元分布图Fig.5 Elements distribution map of Nested sub-array
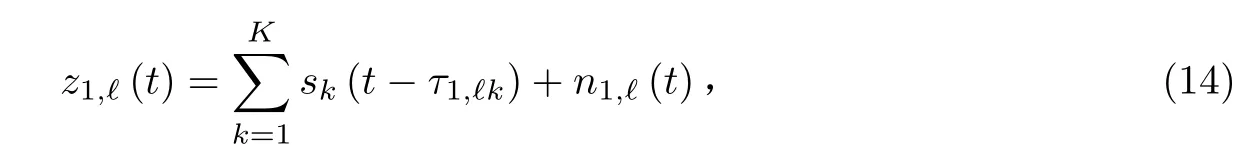
式中:τ1,ℓk=pℓξk/c表示第ℓ个天线与参考天线之间的延时,c为电磁波传播速度,ξk=sinθksinφk表示第k个信号的y轴方向余弦;n1,ℓ(t)为由第一个子阵列的第ℓ个天线测量到的加性高斯白噪声。
第二个子阵列中第ℓ个天线的输出信号表示为

式中:τ2,ℓk= (pℓξk+dxγk)/c表示第二个子阵列上第ℓ个天线与参考天线之间的延时,γk=sinθkcosφk是第k个信号的x轴方向余弦;n2,ℓ(t)为由第二个子阵列的第ℓ个天线测量到的加性高斯白噪声。由式(14)和(15)可知,两个子阵列的流形矩阵都是时变的,传统DOA 估计算法不能直接用于宽带LFM 信号。
本工作利用分数阶傅里叶变换工具,首先把时频域内的宽带问题转换成为频率响应函数(frequency response function, FRF)域内的窄带问题,进而提出新的算法实现Nested 平行阵列的宽带LFM 信号二维测角。
对宽带LFM 信号sk(t)进行FrFT,可得
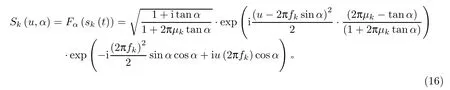
根据FrFT 时移特性,信号sk(t)延时τ后进行FrFT,则有
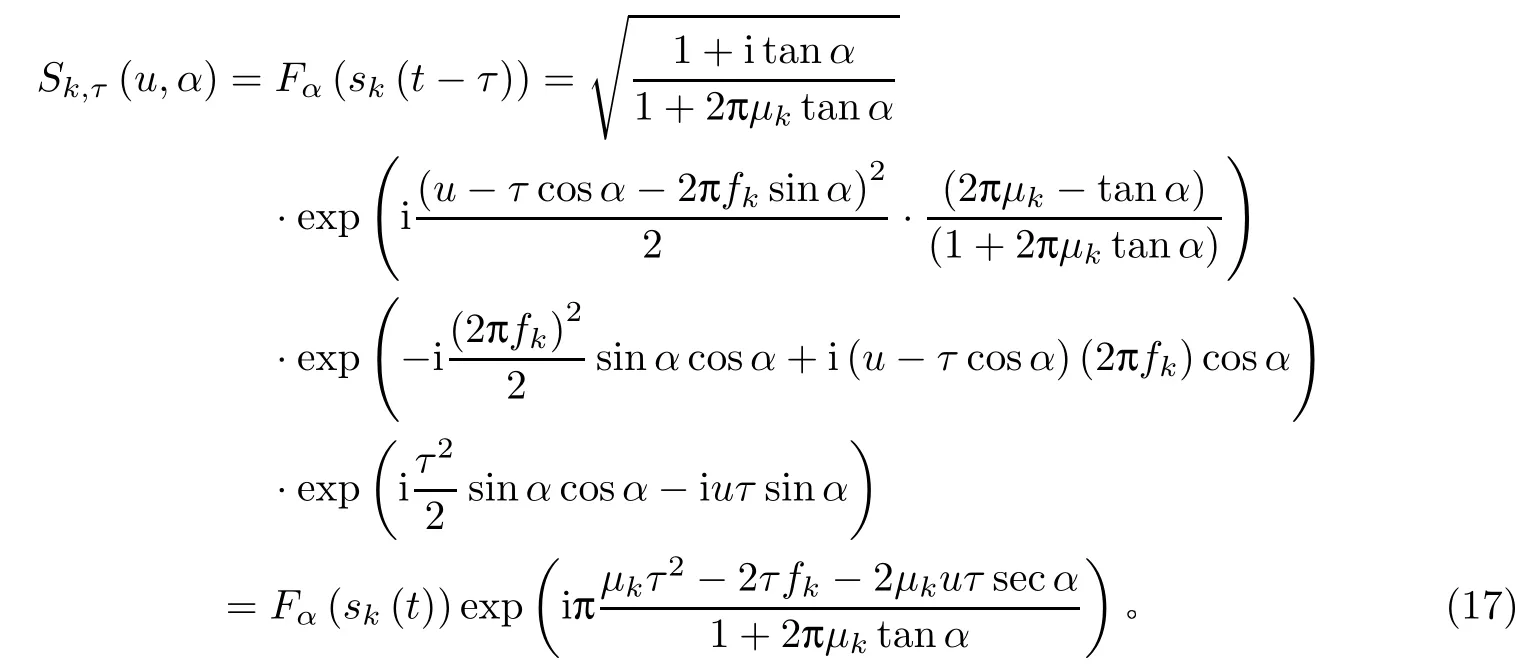
对第一个子阵列中第ℓ个天线的输出信号进行FrFT,根据FrFT 的线性特性可得
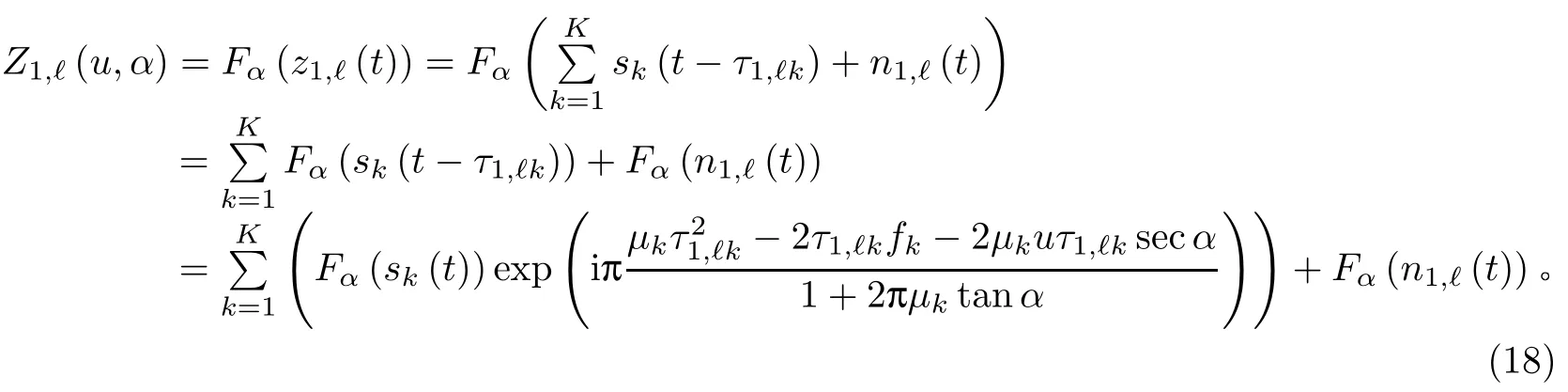
因为FrFT 不改变噪声的时域白特性,也不改变噪声能量,在任何FRF 域,高斯白噪声均不呈现能量聚集,所以零均值高斯白噪声经过FrFT 仍为零均值高斯白噪声[19-20]。
综上所述,在FRF 域,由第一个子阵列测量的宽带LFM 信号可以表示为L×1 维向量:
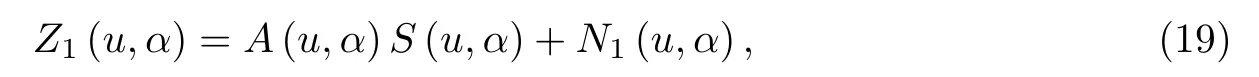
式中:S(u,α) = (S1(u,α),S2(u,α),··· ,SK(u,α))T是K ×1维入射信号向量;N1(u,α) =(N1,1(u,α),N1,2(u,α),··· ,N1,L(u,α))T是L×1 维噪声向量;A(u,α)=(a1(u,α),a2(u,α),··· ,aK(u,α))是L×K维子阵列流形矩阵,ak(u,α)是第k个信号的L×1 维子阵列导向矢量,其表达形式为

类似地,由第二个子阵列测量的L×1 维宽带LFM 信号向量具有形式,
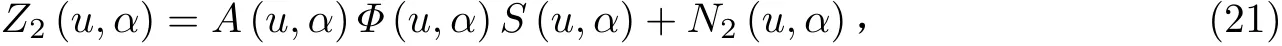
式中:Φ(u,α)是K × K维对角矩阵,它的第k个对角线元素为;N2(u,α) = [N2,1(u,α),N2,2(u,α),··· ,N2,L(u,α)]是第二个子阵的L×1 维加性噪声向量。
本工作讨论的问题是对不同时刻tn(n= 1,2,··· ,N)宽带LFM 入射信号sk(t)的方向(θk,fk) (k= 1,2,··· ,K)进行估计并提出一种Nested 阵列测量宽带信号二维空间角的新算法,为此进行以下假设:①并行Nested 阵列天线特性一致,为全相宽带接收天线;②入射信号为点源信号,各点源相对于Nested 阵列方向唯一确定;③入射信号的数量是预先知道或正确估计的;④入射信号的功率和带宽相等, 且彼此不相干;⑤噪声是均值为0、方差为σ2宽带高斯白噪声,与入射信号不相关。
3 算法推导
3.1 DOA 矩阵公式
所提算法的第一步是构造具有增强自由度的DOA 矩阵。基于上述假设,第一个Nested子阵测量信号的自相关矩阵为

式中:上标H 表示共轭转置;I表示单位矩阵;对角矩阵Rs= diag(ρ1,ρ2,··· ,ρK)是K×K阶入射信号相关矩阵,其中ρk是第k个信源的“聚集”功率。由于Rs是对角矩阵,Ra的向量形式可简化为

式中:上标*代表复共轭;⊙代表Khatri-Rao乘积;ρ=(ρ1,ρ2,··· ,ρK)T;E=(eT1,eT2,··· ,eTL)T,除了第ℓ位置的1 外,eℓ是全零的向量,上标T 是转置算子[21]。由于用特征值估计法可以很容易地估计出式(23)中的噪声功率,因此可以去掉式(23)中的噪声项,得到

接下来,利用Nested 阵列的差分共阵属性,很容易验证(A*⊙A)的每列只有=2L2(L1+1)-1个不同的项。首先,从(A*⊙A)中删除重复行,并对其余行进行排序,使第ℓ行与y轴坐标相关联;然后,可以通过选择va的非重复项来形成一个新的向量va

式中:B(u,α)=(b1(u,α),b2(u,α),...,bK(u,α))是一个阶矩阵,第k列是一个维向量,

很明显,式(25)用流形矩阵B(u,α)和信号向量ρ表示单快拍测向问题。为了估计信号的方向,向量被划分为L2(L1+1)个重叠子向量,每个子向量包含L2(L1+1)个元素。那么,第m个子向量可以表示为

式中:Bm(u,α)是矩阵B(u,α)的第m到(m+L2(L1+1)-1)行。
对于所有m=1,2,··· ,L2(L1+1),可以形成一个L2(L1+1)×L2(L1+1)维矩阵

由于Bm(u,α)与B1(u,α)相关,即

Φξ是一个K×K维对角矩阵,由于第k个对角线项为

因此,可以将V a表示为

式中:D(·)表示通过将矢量放在主对角线上的括号中来生成对角矩阵的运算符。
类似地,由第一和第二Nested 子阵所测信号的互相关矩阵为

Rb的向量形式为
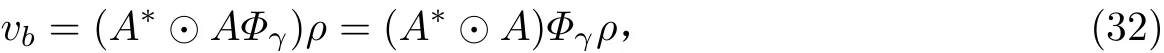
移除重复项,可得

由于向量与具有相同的大小,可以将向量分解为L2(L1+1)个重叠子向量以构造L2(L1+1)×L2(L1+1)矩阵

是的第m到(m+L2(L1+1)-1)行。矩阵可以表示为

基于B的范德蒙结构和前文假设,使用B是全列秩的特性,则有

式中:上标†表示伪逆运算符。从式(35)和(36),可构造如下DOA 矩阵:

3.2 二维空间角度估计
D的特征分解可写为

由式(37)和(38)可以很容易地证明,Φγ的第k个对角元素等于Ψγ的第k个非零对角元素。令[Ψγ]k,k为D的非零特征值,并且设fk(k= 1,2,··· ,K)是与这些特征值相关的特征向量,则x轴方向余弦估计可以从fk估计为
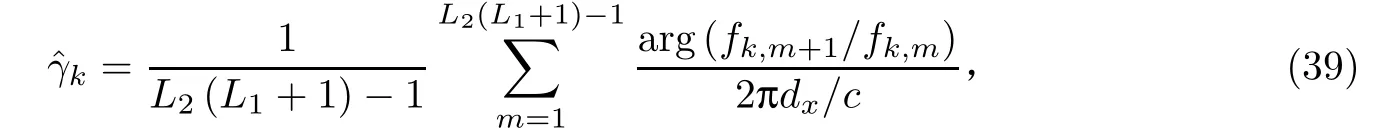
式中:fk,m表示fk的第m个元素。y轴方向余弦估计可通过下式计算得到:


本工作提出的算法从矩阵的特征值估计x轴方向余弦,并且从D的特征向量估计y轴方向余弦ξk。由于特征值及其特征向量是成对的,因此估计的方向余弦和将自动匹配而无需任何额外的配对匹配处理。可以识别的信源的最大数量由D的信号子空间维度确定。由于D的维数为L2(L1+1)×L2(L1+1),因此该算法可以利用2L物理传感器阵列解析K≤L2(L1+1)-1个宽带LFM 信号。
4 仿真结果
为了验证所提算法的分辨性能,使用L1= 3,L2= 2的并行嵌套阵列测量7 个宽带LFM入射信号。设LFM 信号的初始频率分别为0, 50, 100, 150, 200, 230 和280 MHz, 带宽同为300 MHz。本算法首先需要对宽带LFM 信号进行FrFT。图6 为叠加信噪比(signal noise ratio,SNR)为20 dB 白噪声后,初始频率为100 MHz 宽带LFM 信号FrFT 前后的频谱。
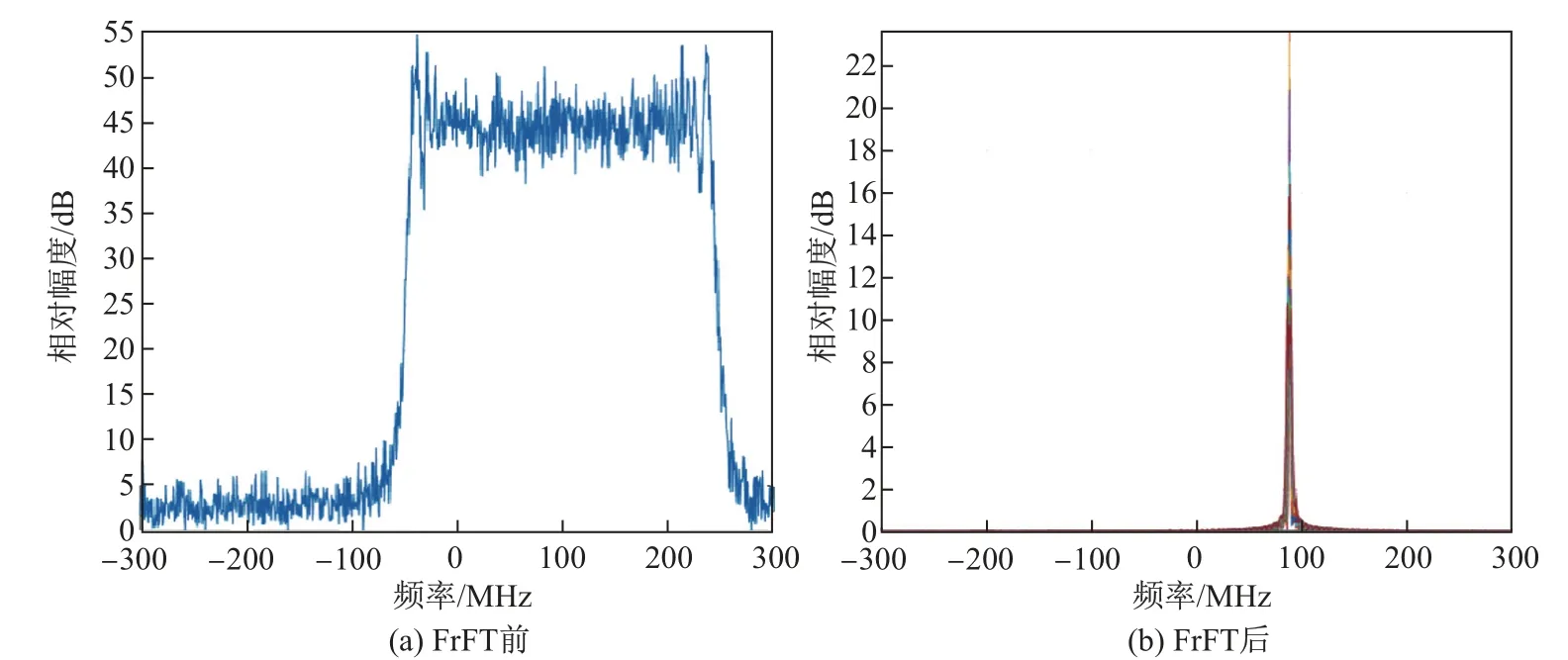
图6 初始频率100 MHz 的LFM 信号FrFT 前后频谱Fig.6 Frequency spectrum of LFM signal before and after FrFT with initial frequency of 100 MHz
若7 个信源的方位、高低角度分别为(30°,10°),(30°,50°),(50°,60°),(80°,20°),(100°,80°),(110°,50°)和(160°,30°),信噪比和快拍数分别设置为20 dB 和1 000,共进行了500 次独立蒙特卡罗试验。图7 为10 次独立运行的空间角估计。从图中可以看出,所提算法可以精确地分辨出这7 个宽带LFM 信号。

图7 空间角实际值与估计结果Fig.7 True values and estimated values of space angles
应用本工作所提算法,将L1=L2=3 的并行嵌套阵列与L=8,L=12 的平行ULA 阵列进行性能对比。对于角度为(10°,50°)的信号入射,图8 为不同阵列结构算法所估计角度的均方根误差随SNR 的变化关系。从图中可以看出,所提算法的性能接近L= 12的平行ULA阵列,而明显优于L=8的平行ULA 阵列。
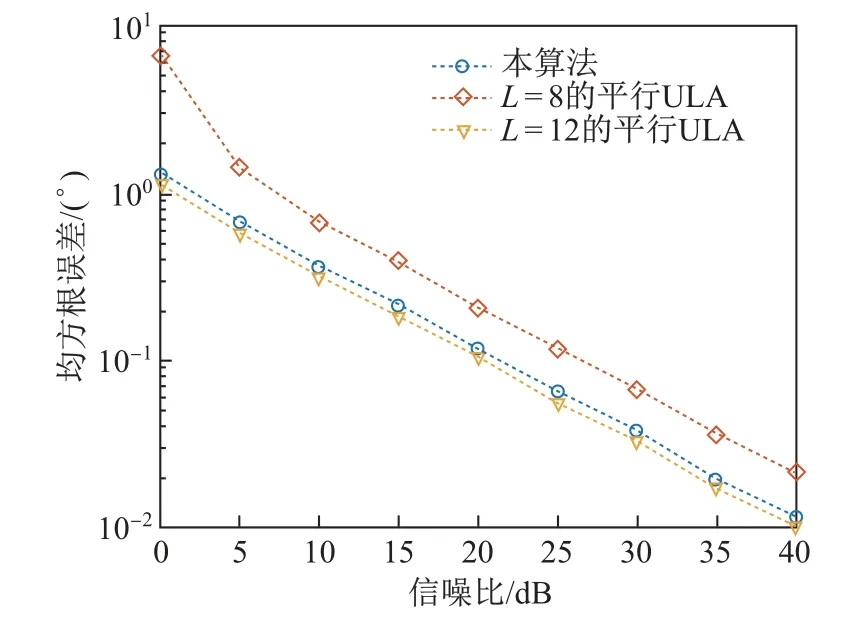
图8 随信噪比变化的均方根误差对比曲线Fig.8 Root mean square error (RMSE) contrast curves as the function of SNR
5 结束语
本工作提出了一种使用平行Nested 阵列来估计宽带LFM 信号二维方向的新算法。该算法的关键思想是首先基于分数阶傅里叶变换,把宽带LFM 信号转换为FRF 域的窄带信号,然后利用嵌入在并Nested 阵列的自相关矩阵和互相关矩阵中的差分共阵列属性,形成具有增强自由度的DOA 矩阵,在不涉及二维非线性搜索和参数匹配的情况下,可实现自动配对的二维角度估计。
