莫尔－库仑屈服准则应力不变量及剪胀角参数表达式与应力符号约定的适配性研究

蔡晓鸿，蔡勇斌，蔡勇平

（1.吉安市水利局，江西 吉安 343000；2.吉安市水利水电规划设计院，江西 吉安 343000）

0 引 言

莫尔－库仑（Mohr－Coulomb）屈服准则由于其解析表达式简明，且有很好的精确度；加之物理力学概念直观明确，参数易于通过简单的试验确定；且未考虑中间主应力σ2的影响，从而应用于实际工程偏安全。特别是在岩土力学与工程仍处于“半理论半经验”设计水准的当下，受荷载分析统计、内力计算组合、内力控制截面选取的误差甚或岩土体计算模型与计算参数取用给不准影响，在真实的建筑结构计算分析中不存在精确解，只存在控制解或优化解的背景下，莫尔－库仑屈服准则为工程界所乐于广泛采用。

然而，在期刊审稿与项目工程设计审查中，常见到不少学术、技术人员在采用莫尔－库仑屈服准则的主应力表达式、应力不变量表达式及塑性流动剪胀角参数表达式，特别是将其应用于水工压力隧洞或隧道工程弹塑性应力计算、流固耦合计算分析时，未注意须与所取用应力符号约定相关联适配，常出现误套误用现象，致使应力计算成果与后续研究产生不应有的错误。为避免这一错误持续发生，我们曾就与水工压力隧洞弹塑性应力计算工况相适配的莫尔－库仑屈服准则主应力表达式的合理取用做过深入分析讨论[1]，并引起水工界的重视。下面，我们将进一步探究莫尔－库仑屈服准则的应力不变量表达式、塑性流动剪胀角参数表达式与应力符号约定、大小主应力顺序间的关联适配性，以使专业技术人员对此有更明晰的认知，避免不当误用。

1 与拉应力为正、压应力为负约定相适配的莫尔－库仑屈服准则应力不变量表达式

在进行水工压力隧洞等建筑物弹塑性应力计算时，莫尔－库仑屈服准则的主应力表达式，是与其应力符号约定及大小主应力顺序相关联协调的，参考文献[1]曾详尽地分析讨论过这一问题，本文不予赘述。由于屈服准则与坐标轴方向的旋转无关，所以屈服准则除采用主应力表示外，常用的另一表示方法是通过应力不变量来描述。下面我们来推求与应力符号约定及大小主应力顺序相适配的莫尔－库仑屈服准则应力不变量表达式。

应力符号采用连续介质弹性力学的约定，即以拉应力为正、压应力为负，相应莫尔－库仑屈服准则的数学表达式为[2]：

式中：σ为岩土屈服面上的剪应力；C为岩土的粘聚力；φ为岩土的摩擦角。

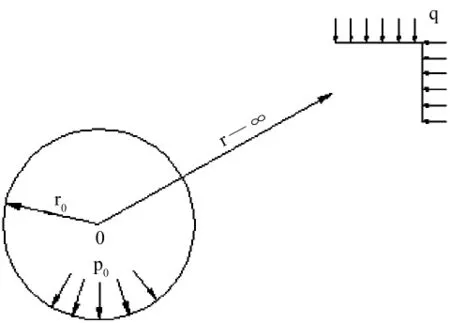
图1 隧洞围岩应力计算简图

当均匀内水压力p0大于原岩压力q时（图1），围岩径向应力σr为小主应力，围岩切向应力σθ为大主应力，其莫尔－库仑屈服准则表达式为（见图 2（a）、（b））[1]：

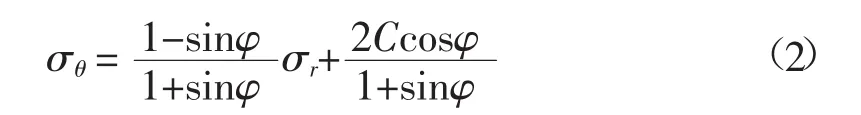
当均匀内水压力p0小于原岩压力q时，则围岩径向应力σr为大主应力，围岩切向应力σθ为小主应力，相应莫尔－库仑屈服准则表达式为（见图2（c））：

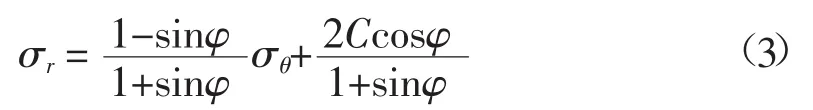
若以σ1和σ3分别表示最大、最小主应力，即有σ1≥σ2≥σ3，则式（2）、（3）可统一于一个表达式：

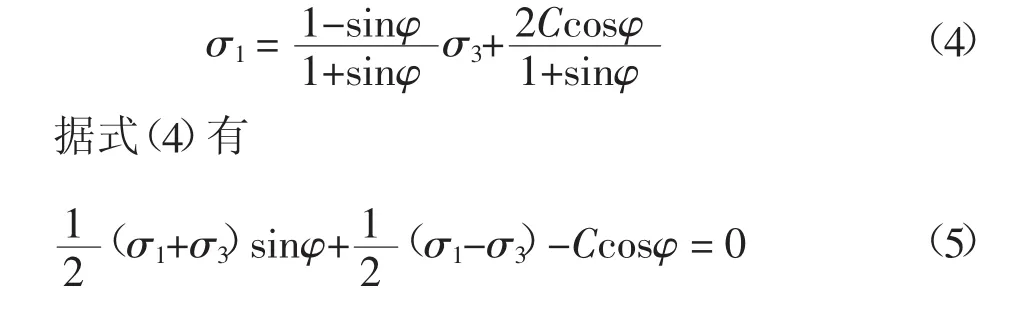
下面我们来推求岩土材料莫尔－库仑屈服准则的应力不变量表达式。将式（5）改写成：

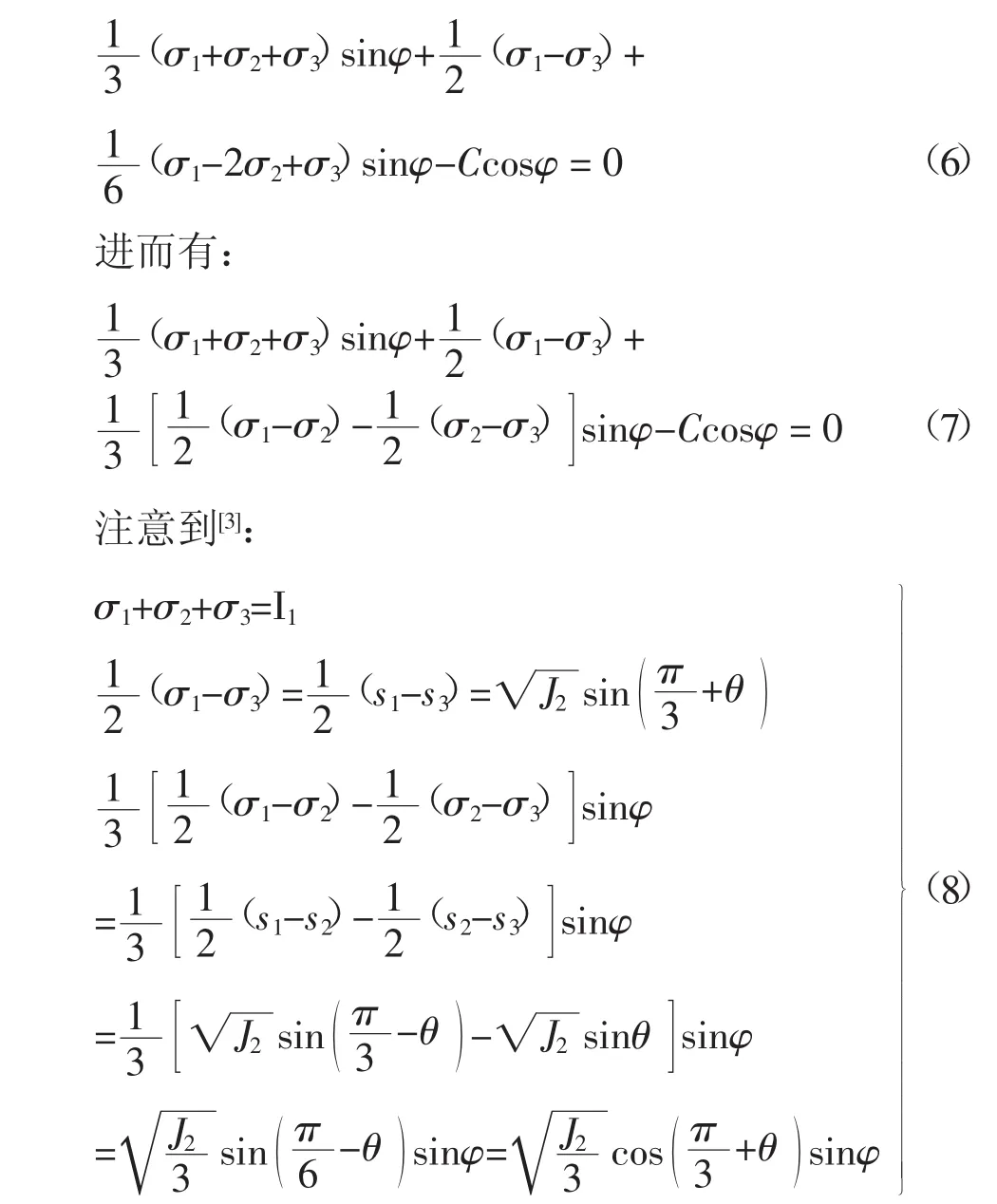
式中：I1为应力张量的第一不变量；s1、s2、s3为主应力偏量；J2为偏应力张量的第二不变量；θ为相似角（Lode角）。

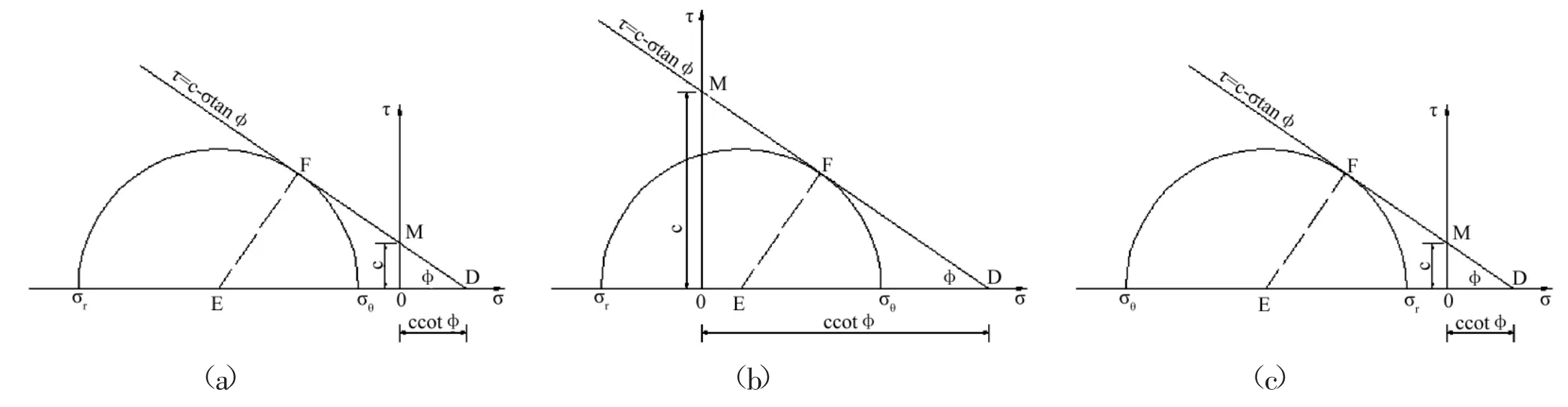
图2 莫尔-库伦屈服准则（拉应力为正，压应力为负）

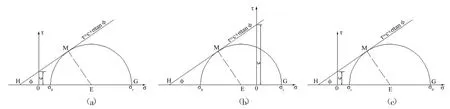
图3 莫尔-库伦屈服准则（压应力为正，拉应力为负）

将式（8）代入式（7），则得与拉应力为正、压应力为负应力符号约定相适配的岩土材料莫尔－库仑屈服准则应力不变量表达式：

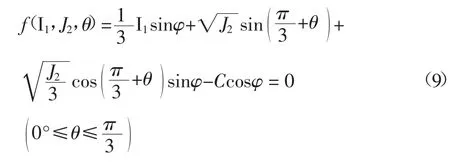
2 与压应力为正、拉应力为负相适配的莫尔－库仑屈服准则应力不变量表达式

应力符号采用岩土力学的约定，通常以压应力为正、拉应力为负，莫尔－库仑屈服准则的数学表达式为：

此时，若均匀内水压力p0大于原岩压力q，围岩径向应力σr为大主应力，围岩切向应力σθ为小主应力，其莫尔－库仑屈服准则表达式为（图 3（a）、（b））：

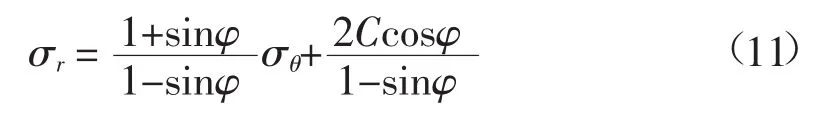
若均匀内水压力p0小于原岩压力q，围岩径向应力σr为小主应力，围岩切向应力σθ为大主应力，其莫尔－库仑屈服准则表达式为（图3（c））：

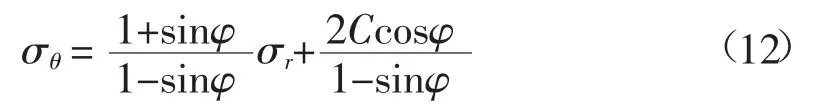
以大、小主应力σ1≥σ2≥σ3描述岩土材料莫尔－库仑屈服准则，则式（11）、（12）可统一于一个表达式：

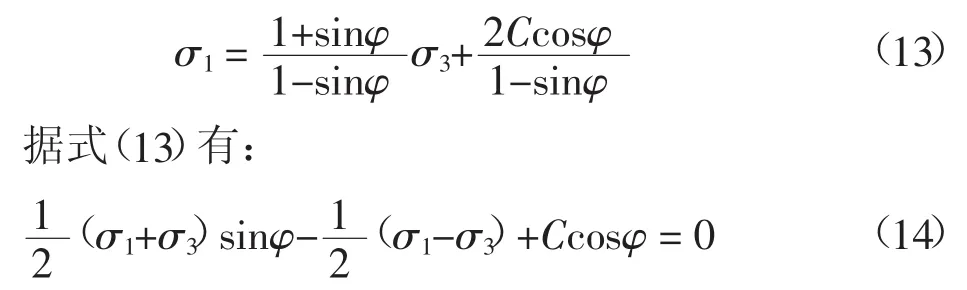
将式（14）改写为：

将式（8）代入式（15），整理得与压应力为正、拉应力为负应力符号约定相适配的岩土材料莫尔－库仑屈服准则应力不变量表达式：

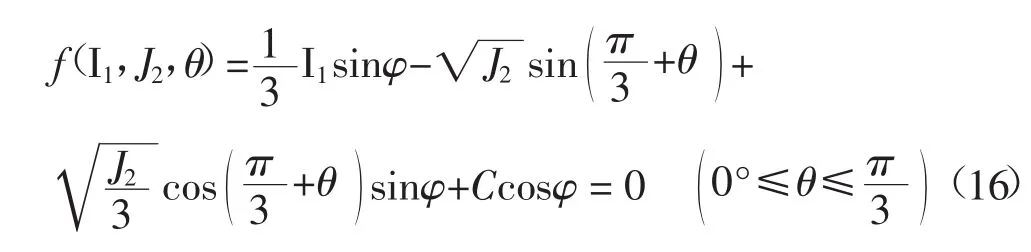
比较式（9）、式（16）可知，莫尔－库仑屈服准则的应力不变量表达式，是与应力符号约定、主应力大小顺序相关联的。而以往在工程学术技术界，往往疏忽了这一相关联性，存在采用弹性力学应力符号约定，而误用与岩土力学应力符号约定相关联的莫尔－库仑屈服准则应力不变量表达式问题，致使后续理论探求与应力计算分析产生不应有的错误。

3 剪胀角参数表达式与应力符号约定的适配性

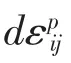
当应力符号采用塑性力学以拉应力为正、压应力为负约定时，利用式（5），岩土材料的莫尔-库仑屈服准则表达式可写成

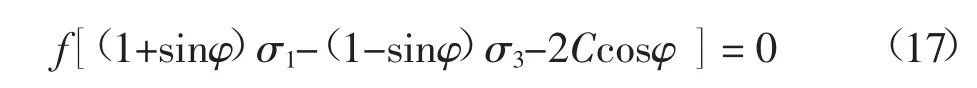
与之相适应的流动法则可以用下式表达[3]：

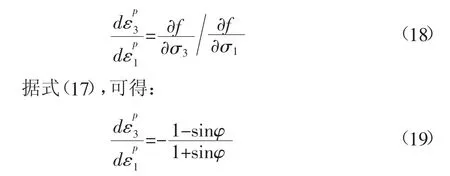
引入塑性流动剪胀角参数αψ，令，

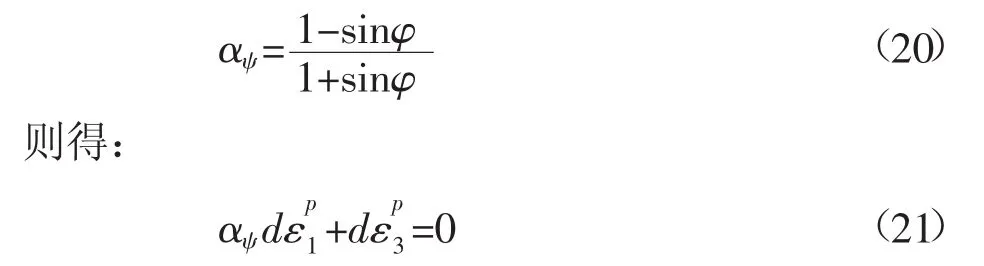
类似，当应力符号采用岩土力学以压应力为正、拉应力为负约定时，利用式（14），岩土材料的莫尔-库仑屈服准则表达式可写成：

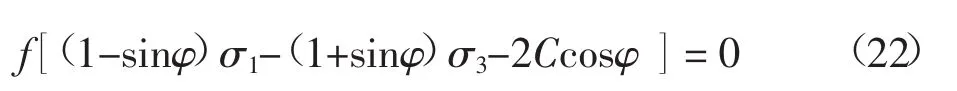
相适应的流动法则可以用下式表达：

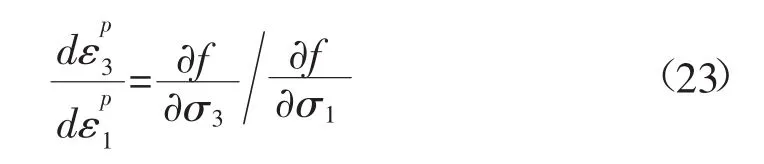
于是据式（22），可得：

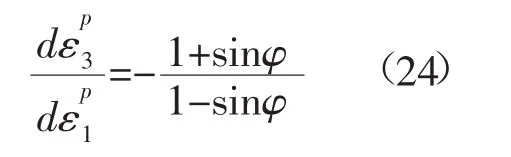
引入塑性流动剪胀角参数βψ，令，

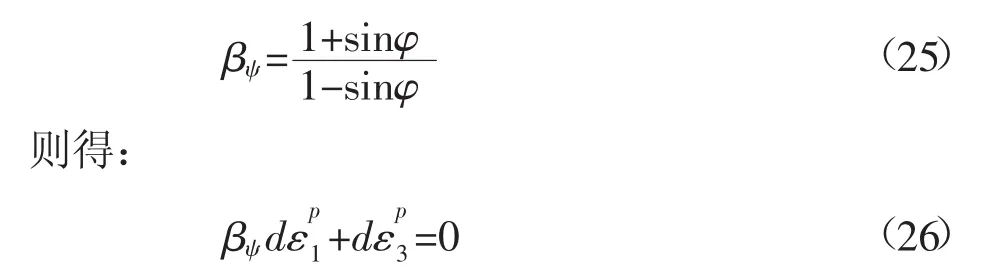
比较式（21）、式（26）可知，与莫尔-库仑屈服准则相关联流动法则的剪胀角参数αψ、βψ表达式，是与应力符号约定及主应力大小顺序相联系的，而以往人们对此认知并不明晰，被许多工程师所疏忽，以致误套误用。有必要指出，考虑到遵守非关联流动法则的岩土材料模型，在应力增量中，塑性应变增量也是线性的，而且满足连续性条件，从而式（21）、式（26）对于非关联流动法则的岩土材料也是适用的。

4 结语

通过推求不同应力符号约定与大小顺序下的莫尔-库仑屈服准则应力不变量表达式及塑性流动剪胀角参数表达式，揭示了莫尔-库仑屈服准则主应力表达式、应力不变量表达式及塑性流动剪胀角参数表达式与应力符号约定、主应力大小顺序间的关联适配性，为正确选用莫尔-库仑屈服准则表达式及塑性流动剪胀角参数表达式提供了指南。显然，关于这一问题讨论的普适性，可推广到其他屈服准则。

有必要指出，将式（1）、（4）、（9）、（20）中 φ 用-φ 代入，则可分别导得式（10）、（13）、（16）、（25），即莫尔-库仑屈服准则主应力表达式、应力不变量表达式及塑性流动剪胀角参数表达式与应力符号约定间的关联式，可转换为与φ的正负号选择相适配，即应力符号以拉应力为正，压应力为负，则相应φ取负号（即莫尔-库仑屈服直线与σ负轴间的夹角）；应力符号以压应力为正，拉应力为负，则相应φ取正号（即莫尔-库仑屈服直线与σ正轴间的夹角），而这便从理论上揭示了莫尔-库仑屈服准则应力符号不同约定间的内在联系，为采用弹性力学数值计算方法及其应力符号约定求解莫尔-库仑屈服准则岩土工程问题提供了一条捷径，打开了一扇互通之门。