Linguistic Single-Valued Neutrosophic Power Aggregation Operators and Their Applications to Group Decision-Making Problems
2020-05-22HarishGargandNancy
Harish Garg and Nancy
Abstract—Linguistic single-valued neutrosophic set (LSVNS) is a more reliable tool, which is designed to handle the uncertainties of the situations involving the qualitative data. In the present manuscript, we introduce some power aggregation operators(AOs) for the LSVNSs, whose purpose is to diminish the influence of inevitable arguments about the decision-making process.For it, first we develop some averaging power operators, namely,linguistic single-valued neutrosophic (LSVN) power averaging,weighted average, ordered weighted average, and hybrid averaging AOs along with their desirable properties. Further, we extend it to the geometric power AOs for LSVNSs. Based on the proposed work; an approach to solve the group decision-making problems is given along with the numerical example. Finally, a comparative study and the validity tests are present to discuss the reliability of the proposed operators.
I. Introduction
MULTIPLE criteria group decision-making (MCGDM)problems seek great attention to practical fields, whose main objective is to determine the most desirable alternative to the finite alternatives according to the preference values of the criteria given by different decision makers. However, in order to process the imprecision in data, fuzzy set (FS) [1] and intuitionistic fuzzy set (IFS) [2] theories are the most successful ones, which characterize the criterion values in terms of membership degree. Numerable attempts have been made by different researchers in processing the information values using different operators under these environments [3]–[13]. It is remarked that neither the FS nor IFS theory is able to deal with indeterminate and inconsistent data. For instance, consider an expert which gives their opinion about a certain object in such a way that 0.5 being the “possibility that the statement is true”, 0.7 being the “possibility that the statement is false” and 0.2 being the “possibility that he or she is not sure”.To resolve this, Smarandache [14] introduced a new component called the “indeterminacy-membership function” and added to the “truth membership function” and “falsity membership function”, all which are independent of each other and lying inand the corresponding set is known as a neutrosophic set (NS). NS theory handles the indeterminate information, but this theory is hard to implement on the practical problems, therefore, Wanget al. [15] presented the single-valued neutrosophic (SVN) set (SVNS), a special case of NSs.Due to its importance, several researchers have made their efforts to enrich the concept of neutrosophic sets in the decisionmaking process.
In order to evaluate the given information in decisionmaking, the important aspect of solving the problem is to design an appropriate mathematical function which aggregates the different preference of the decision makers into the collective ones. In that direction, Ye [16] presented the operational laws of SVNSs and SVN weighted average and geometric (WAG) AOs (aggregation operators) denoted by single-valued neutrosophic weighted average (SVNWA) and single-valued neutrosophic weighted geometric (SVNWG).Penget al. [17] defined the improved operations of SVN numbers (SVNNs) and developed their corresponding ordered WAG AOs. Nancy and Garg [18] developed the WAG operators by using the Frank norm operations. Later on, some different kinds of the AOs have been proposed by the authors in [19]–[22].
All these above operators, aggregate the given criterion values without considering the precedence relationship among them. To get rid of this flaw, Wuet al. [23] defined the prioritized WAG operators for SVNNs. Liu and Wang [24]developed the prioritized ordered WAG operators while Jiet al. [25] established the single-valued prioritized Bonferroni mean operator by using the Frank operations. Garg and Nancy[26] developed a nonlinear programming based TOPSIS(“Technique for order preference by similarity to ideal solution”)approach for solving the decision-making problems under the interval NS environment. Yang and Li [27] extend the power operator to NS domain. Aside from these, various authors incorporated the idea of NS theory into the different fields[28]–[32].
In the neutrosophic environment, the information which is evaluated is quantitative in nature and is expressed by the means of numeric numbers. But in real applications, the ‘decisionmakers’ opinions or preferences is usually uncertain due to increase in complexities and the subjective nature of human thoughts. Thus, the exact numbers are not the best option to represent such kind of qualitative information. For this, a new concept, namely, linguistic variables (LVs) [33] has been established to access the information which cannot estimate by exact numbers. Due to the great importance of linguistic variables, it has become the hot topic of research among the researchers. Based on this idea, Liet al. [34] introduce the linguistic neutrosophic sets (LNSs) in which membership,indeterminacy, and non-membership is expressed as a LV instead of real numbers and also proposed some Heronian mean operators. Fang and Ye [35] introduced most basic aggregation operators, namely, Linguistic neutrosophic number WAG operators. Garg and Nancy [36] presented some neutrosophic prioritized AOs under the linguistic SVNS (LSVNS)environment.
As these basic operators are crucial tools in the aggregating process and easily gives the best choice according to the given information, but these operators skip the consideration of the relationship between the given data. In the present work, we introduce different types of power AOs in LSVNS environment. The LSVNS can easily express the uncertain qualitative information in the best way and power AO provides more versatility in the information aggregation process. To get the advantage of both LSVNS and power aggregation, we proposed power AOs for linguistic singlevalued neutrosophic numbers (LSVNNs) of two types: The first type of power aggregation operators aggregates the input data by assigning the weights based on the support function and the second type of power operators considers not only the existing evaluated weights but also use the weights evaluated from support function. Further, the basic properties of these operators have been figuring out. In the end, a method for solving the MCGDM problems has been presented and then applies this approach to a practical example.
The rest of the work is summarized as: Some basic features related to NSs and the LNSs are presented in Section II. In Section III, operational laws and based on it, some series of LSVN power weighted AOs have been proposed along with their certain properties. Section IV established the group decision-making approach based on the proposed operators and validate with a numerical example. Lastly, the conclusion has been summarized in Section V.
II. Preliminaries
In this section, some basic concepts on NSs over the universal sethave been reviewed.
Definition 1 [14]:A neutrosophic set (NS) α overis given by
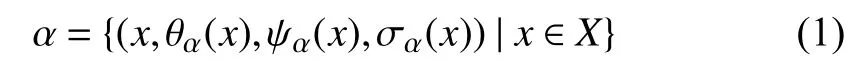
Definition 2 [35]:Letbe a linguistic term set (LTS) with odd cardinalityandThen, a LSVNSAinXis defined as

Definition 3 [35]:In order to compare the LSVNNs, a scoreand an accuracy functioncan be represented asandfor LSVNNThus, based on these functions, an order relation between two LSVNNsanddenoted byis defined if eitheror
Definition 4 [37]:Letandbe two LSVNNs. Then, the distance betweenandis given below:
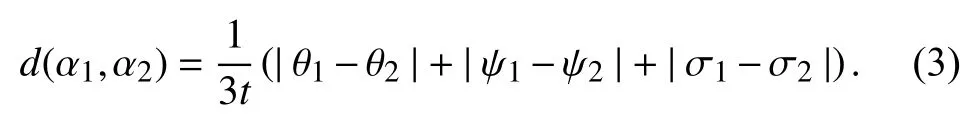
Definition 5 [38]:Let’ attributes then the power averaging (PA) operator is defined as
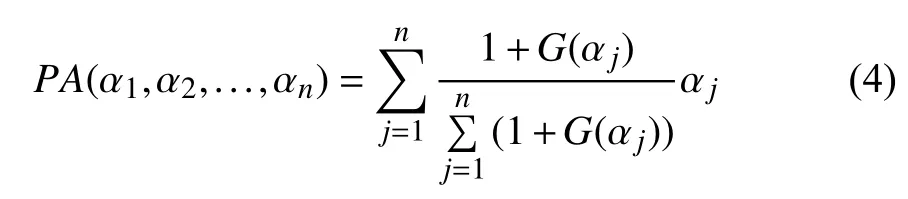
1)supp(αj,αk)∈ [0,1];
2)supp(αj,αk)=supp(αk,αj);
Definition 6 [35], [36]:Letandbe three LSVNNs, then
Definition 7 [12]:A functionis called t-norm if it satisfies the boundary, monotonicity,commutativity and associativity. On the other hand, a functiondefined byis called t-conorm. The t-normis generated by a decreasing function( withand the t-conormis generated aswhere
III. Power Aggregation Operator for Linguistic Neutrosophic Sets
In this section, some new power AOs for linguistic neutrosophic sets namely, linguistic single-valued neutrosophic-power weighted average (LSVN-PWA),linguistic single-valued neutrosophic-power ordered weighted average (LSVN-POWA), linguistic single-valued neutrosophicpower weighted geometric (LSVN-PWG), Linguistic singlevalued neutrosophic-power ordered weighted geometric(LSVN-POWG) etc., have been presented to aggregate the LSVNNs.
A. Operations Laws for LSVNNs
In this section, based on generatorsa ndwe defined the operational laws for LSVNNs as follows.
Definition 8:Letandbe three LSVNNs and a real λ >0, we have
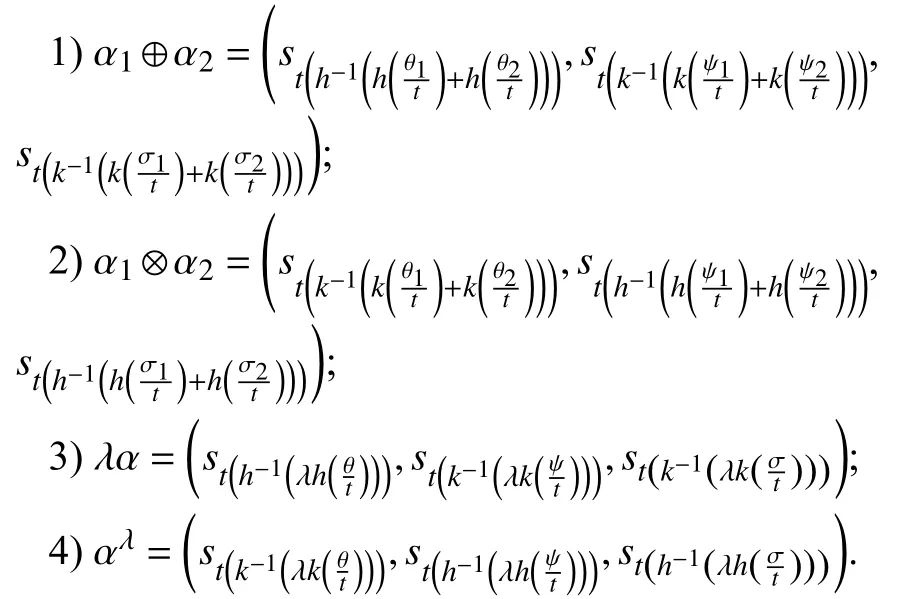
Theorem 1:The operations laws defined in Definition 8 are again LSVNNs.
Proof:Sinceis a decreasing map andtherefore, we getandTherefore,is LSVNN. Similarly,andare LSVNNs. ■
Theorem 2:Letandbe three LSVNNs andbe three positive real numbers, then
Proof:We shall prove only the parts iii) and remaining parts done similarly.

Remark 1:We inspect some special cases ofand

Next, we propose some averaging and geometric power AOs for a collection of LSVNNsdenoted bywith the condition thatfor anyj.
B. LSVN Power Averaging Operator
Definition 9:A linguistic single-valued neutrosophic- power averaging (LSVN-PA) aggregation operator is a mapping LSVN-PA:defined by
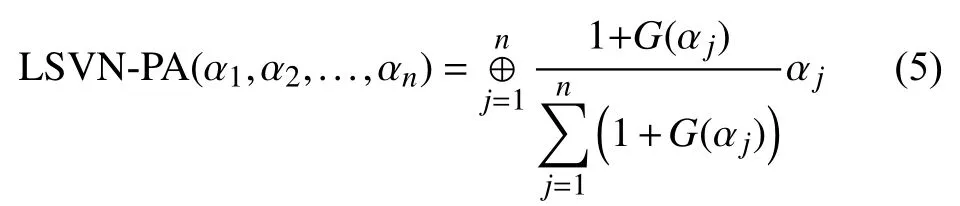
Theorem 3:The aggregated value by LSVN-PA operator is still a LSVNN and is given as

Proof:We will verify (6), by applying the mathematical induction onFor the sake of simplicity, we takeThen, the following steps of the mathematical induction have been followed for
Step 1:Forwe haveand real numberswe haveandTherefore,
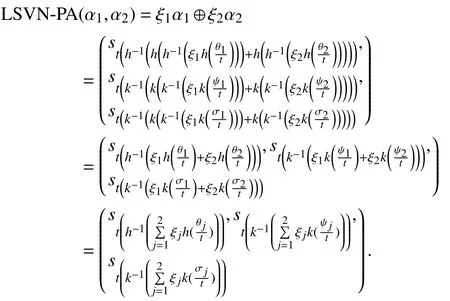
Step 2:Assume that (6) is true forThen, forwe have
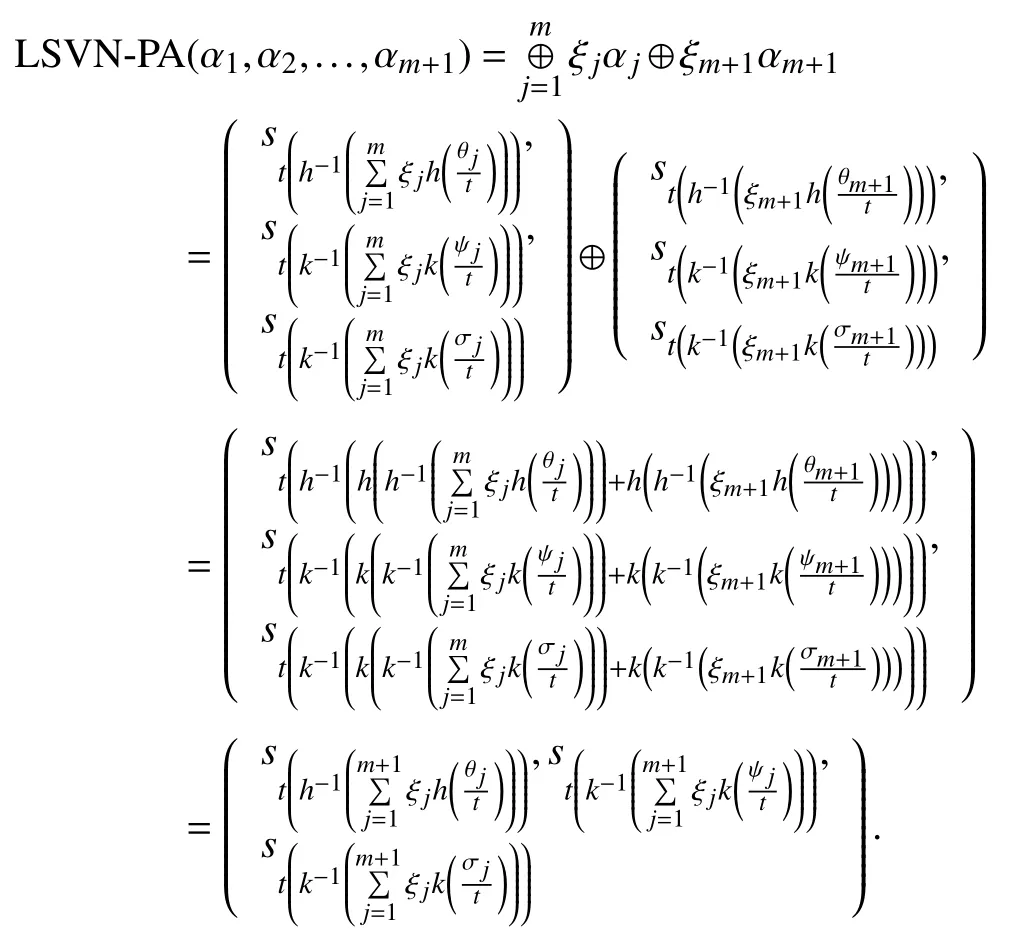
Example 1:Letandα3=be three LSVNNs. Based on the support function of LSVNNs, we get=1.6250,=1.7083 and=1.6667 and hencebecomesandTakeand by considering the additive generatorsifwithk(0)= ∞ andifwithcorresponding to t-norm and t-conorm, respectively.Then, by utilizing this information we get

Further, the LSVN-PA operator satisfies certain properties which are stated as below. Here, for simplicity, we denote
Theorem 4 (Idempotency):Ifthen LSVN-PA
Proof:AsThusand therefore by LSVN-PA operator we have=■
Theorem 5 (Monotonicity):Letandbe two LSVNNs such thatfor allj, thenfor a fixed
Proof:SinceandAlso,is decreasing andis increasing map. Thus, for a fixedthe following equations holds:
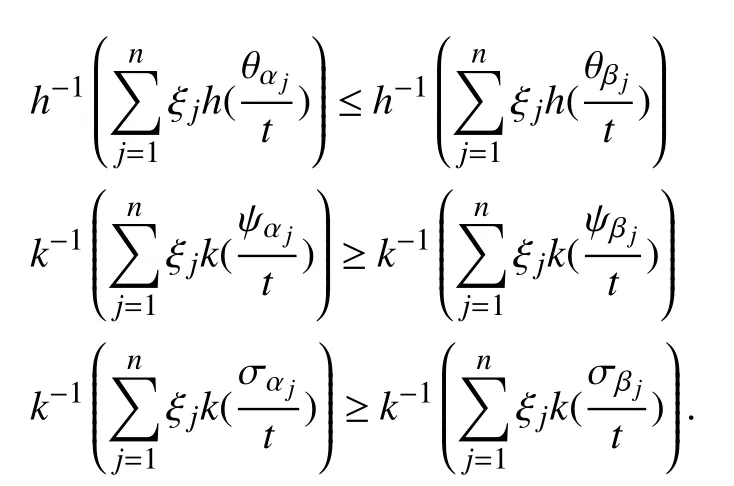
By using the definition of score function of LSVNNs, we get
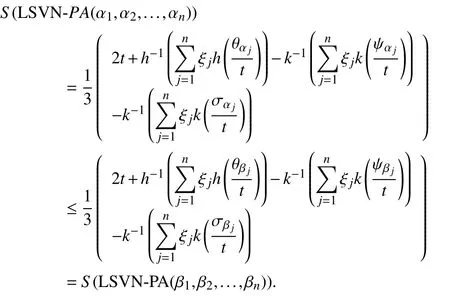
Hence,LSVN-PA(α1,α2,...,αn)≤ LSVN-PA(β1,β2,...,βn).
Theorem 6 (Boundedness):Ifandthen
Proof:For LSVNNswe haveSince the generatorsare decreasing and increasing maps,respectively, therefore, by
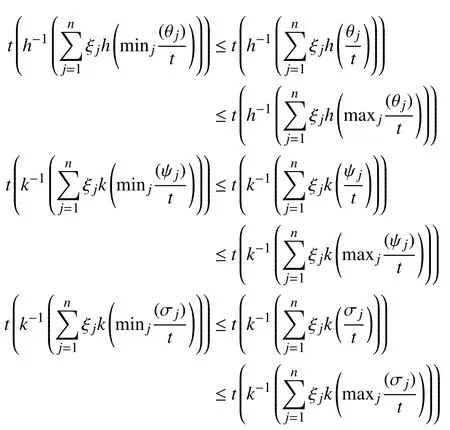
which implies

Now, by using Definition 6, we have

and

Theorem 7 (Shift Invariance):For LSVNNs,β=andwe have LSVN-PA
Proof:By using the addition law for any two LSVNNs, we get
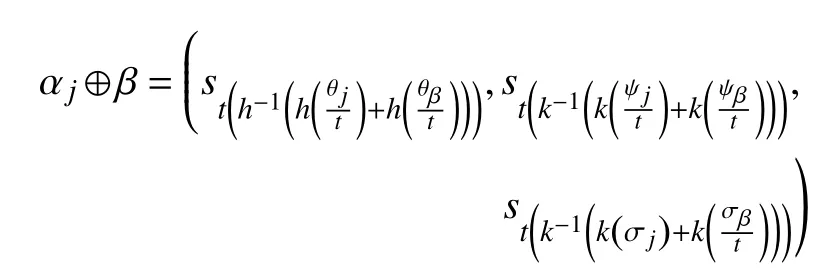
Thus, by using (6), we have

Theorem 8 (Homogeneity):For any real numberwe have
Proof:Asbe a LSVNN,andbe a real value, therefore, we getNow,
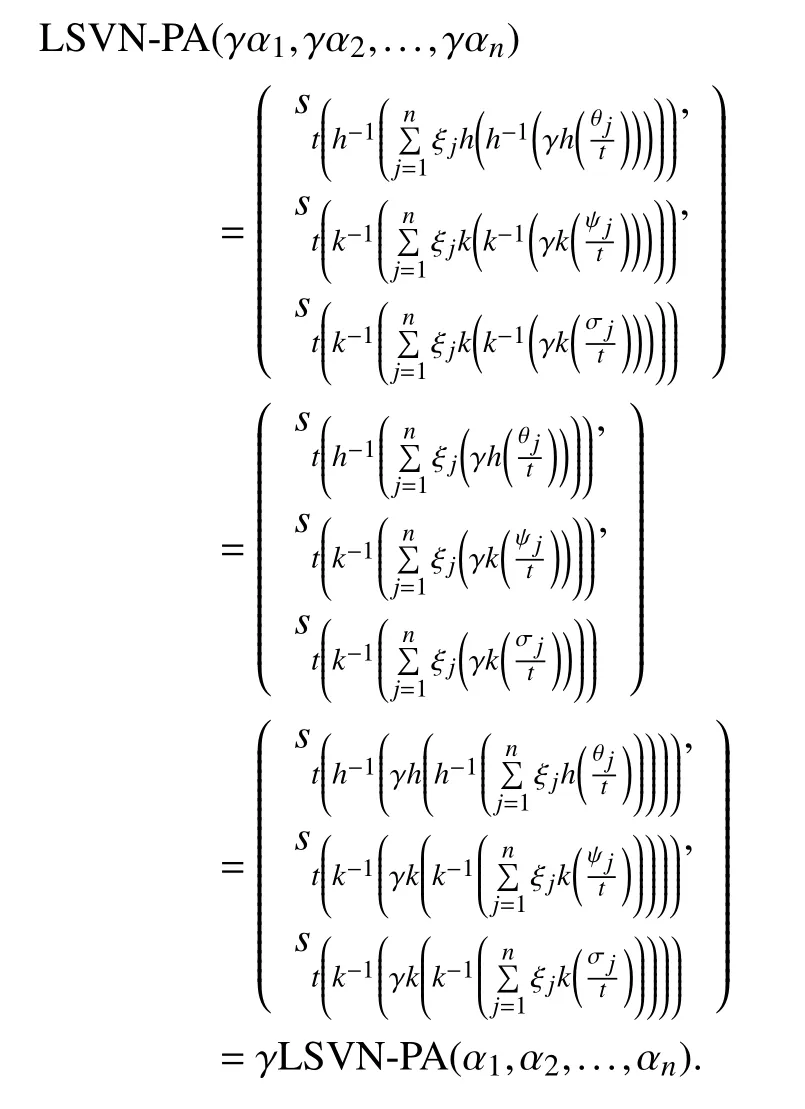
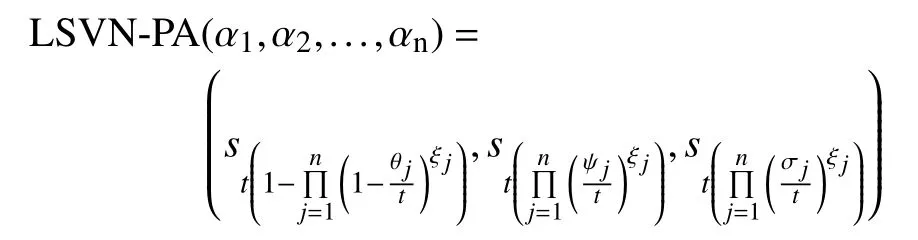
and called as LSVN Archimedean power averaging operator.
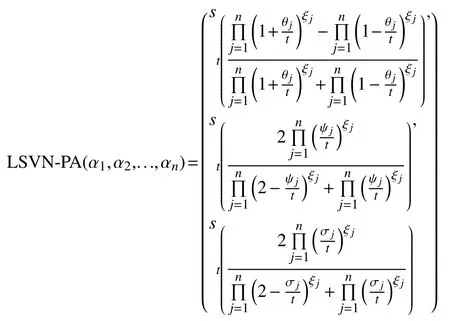
and called as LSVN Einstein power averaging operator.
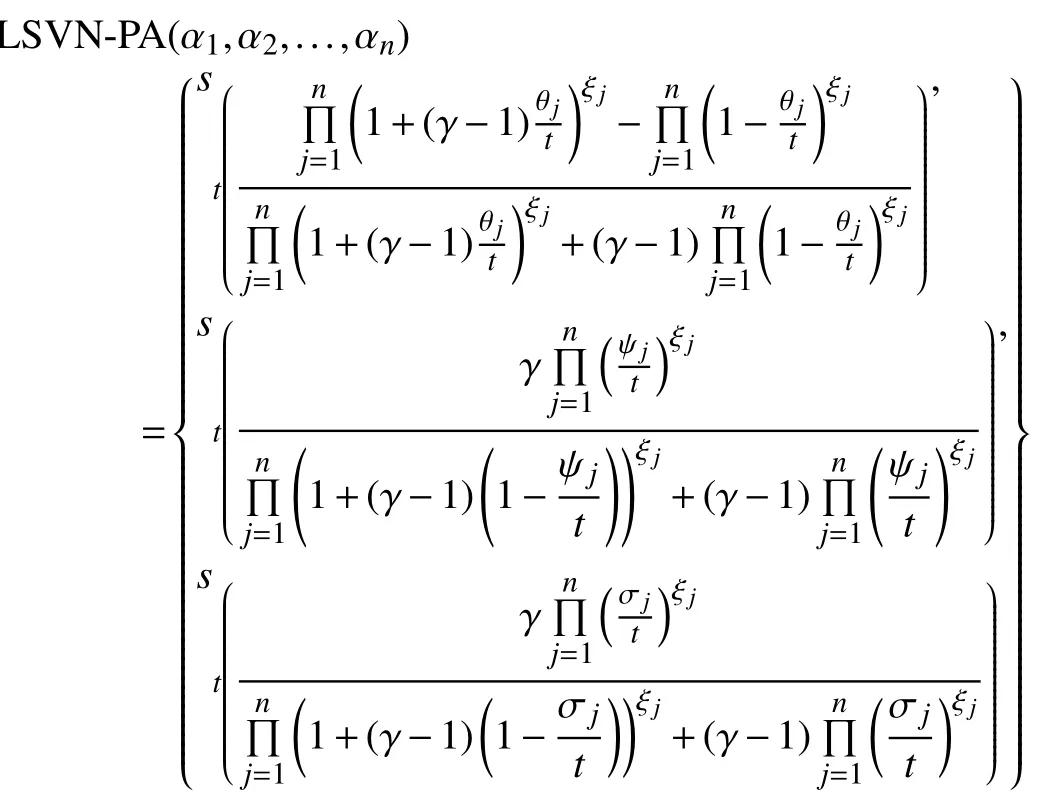
and called as LSVN Hamacher power averaging AO.
C. Weighted Power Aggregation Operator
In this section, we defined some weighted power AOs for LSVNNs.
Definition 10:A LSVN power weighted averaging (LSVNPWA) operator is a mappingdefined as
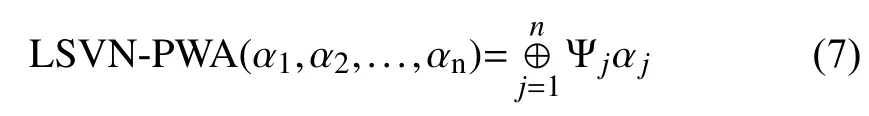
Theorem 9:The aggregated value by LSVN-PWA operator for a collection of LSVNNsis again LSVNN and is given by
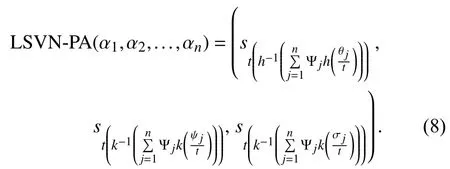
Proof:Similar to Theorem 3. ■
Example 2:Letandbe three LSVNNs andis the weight vector ofBased on it, we getand1.6667. Takeand consider the additive generator as:ifwe have
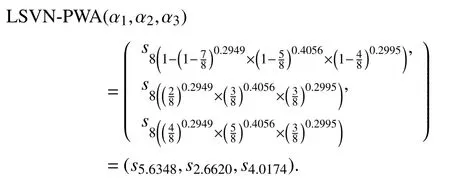
Further, as similar to LSVN-PA operator, it can be easily verified that the LSVN-PWA operator also has the properties of being boundedness, shift-invariance etc.
D. Ordered Weighted Power Averaging Operator
Definition 11:A LSVN power ordered weighted averaging(LSVN-POWA) operator is a mapping LSVN-POWA:that has an associated weight vector ω =(ω1,ω2,...,such thatandand is defined as
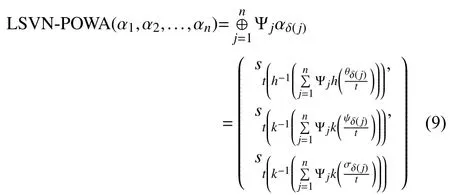
Example 3:Consider the data set as mentioned in Example 2. Then the score values of the LSVNNs areandSinceS(α2), therefore,andwhich givesandThus, we get
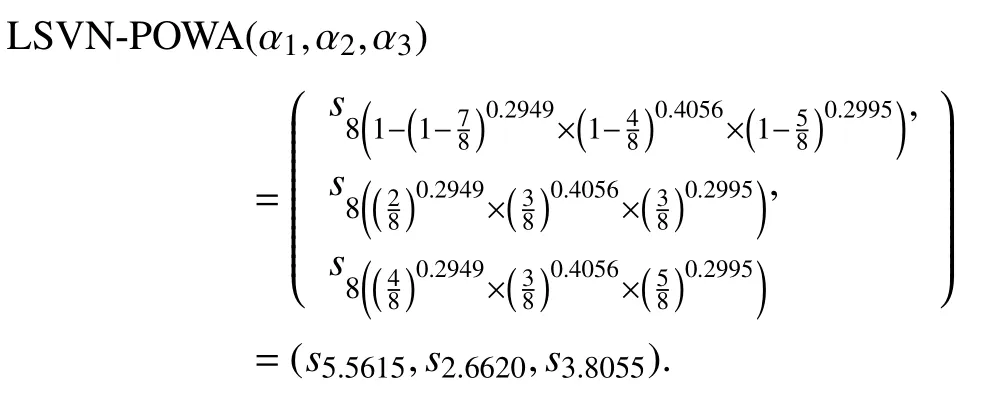
Furthermore, LSVN-POWA operator also satisfies the properties of indempotency and boundedness.
E. Power Hybrid Averaging Operator
Definition 12:A LSVN power hybrid averaging (LSVNPHA) operator is a mapping defined as LSVN-PHA:and given by
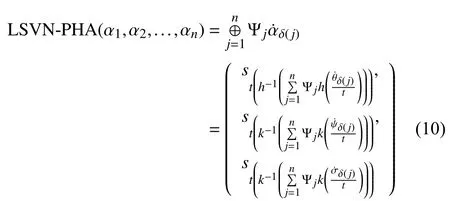
Example 4:Letandbe three LSVNNs,be corresponding weight vector, then, we evaluateby using the additive operatoras below:
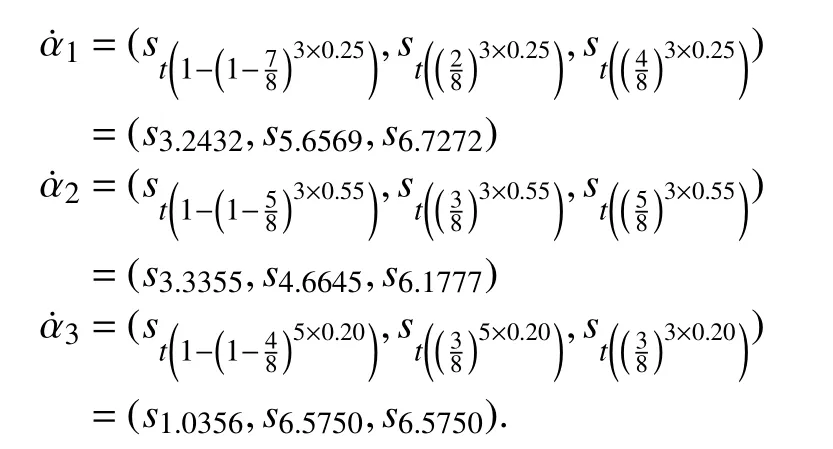
Then, based on the score values ofwe getandAssume that0.3)Tis the importance associated with LSVN-PHA operator and by using support we have,andand thereforebecomesThus, by taking additive operatorwe get

F. LSVN Power Geometric AOs
In this section, we presents some series of LSVN power geometric aggregation operators.
Definition 13:A LSVN power geometric (LSVN-PG)operator is a mapdefined on a collection of LSVNNas
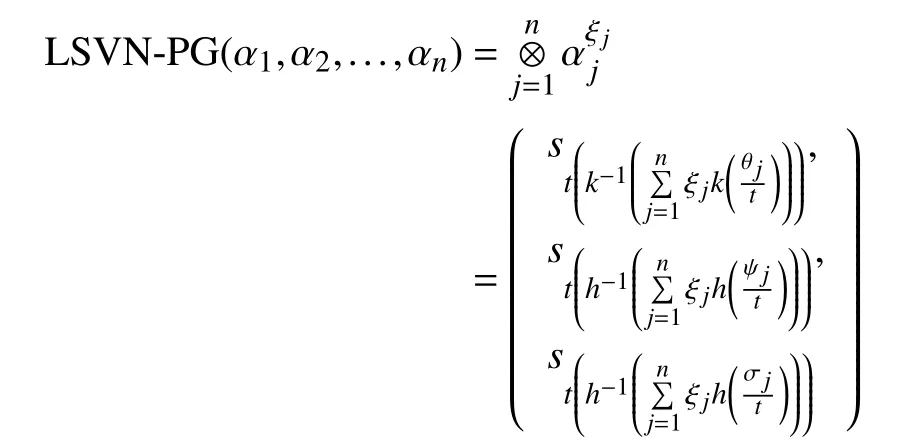
Definition 14:A LSVN power weighted geometric (LSVNPWG) operator is a mappingand defined as

Definition 15:A LSVN power ordered weighted geometric(LSVN-POWG) operator is a mappingthat has an associated weight vectorsuch thatandand is defined as
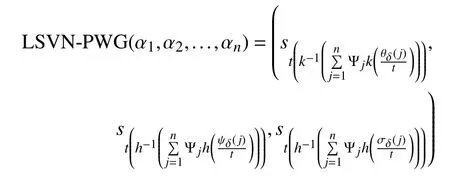
Definition 16:A LSVN power hybrid geometric (LSVNPHG) operator is a mappingdefined on a collection of LSVNNas

Further, as similar to power averaging AOs, it has been observed that the above defined geometric operators also have the property of boundedness and idempotent.
IV. MCGDM Approach Based on Proposed Operators
In this section, an approach to decision-making problems has been established by using the above AOs which is followed by a practical example.
A. Proposed Approach
Consider a decision-making problem which consists ofalternativesandcriteriahaving the weight vectorsuch thatandAssume that a set ofdecision makershave evaluated these alternatives and give their preferences in terms of LSVNNs and their overall preference values are summarized in the decision matrixwhereBased on these information, the following steps of the proposed approach, to find the best alternative(s), have been summarized as follows:
Step 1:Calculateas follows:
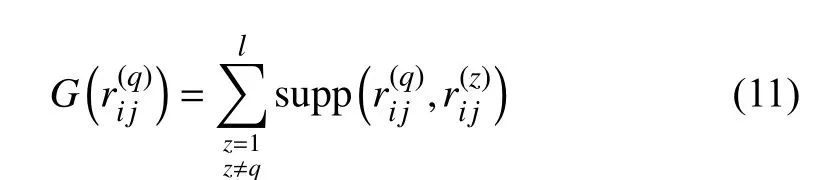
Step 2:Utilize the power average or geometric aggregation operator to aggregate the preference values of each decision maker into the collective one and represented aswhich are computed as:
i) By using LSVN-PA operator
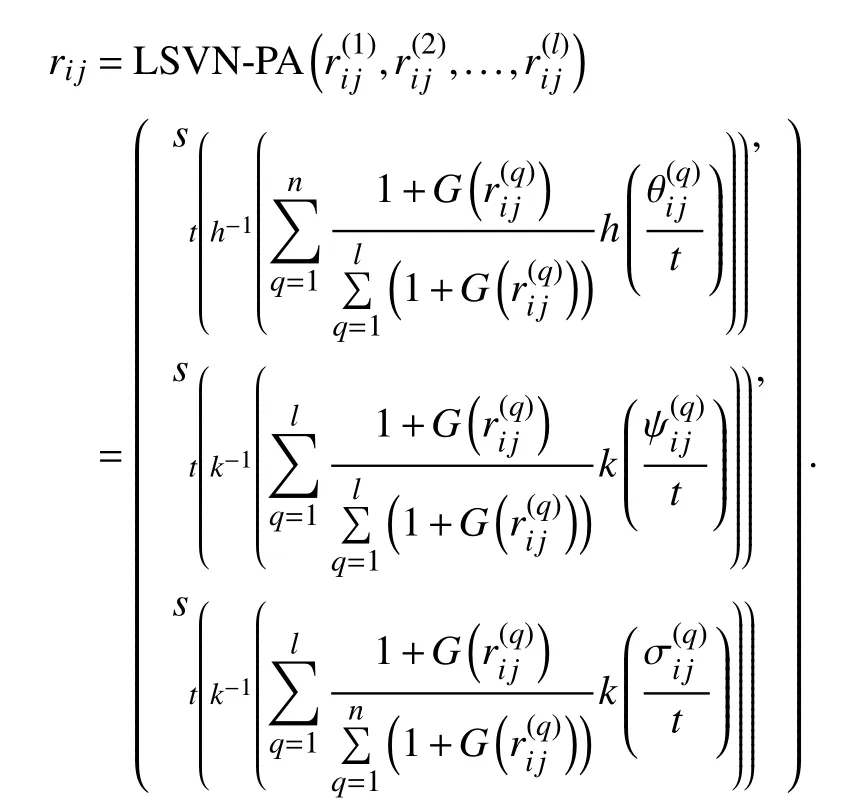
ii) By using LSVN-PG operator
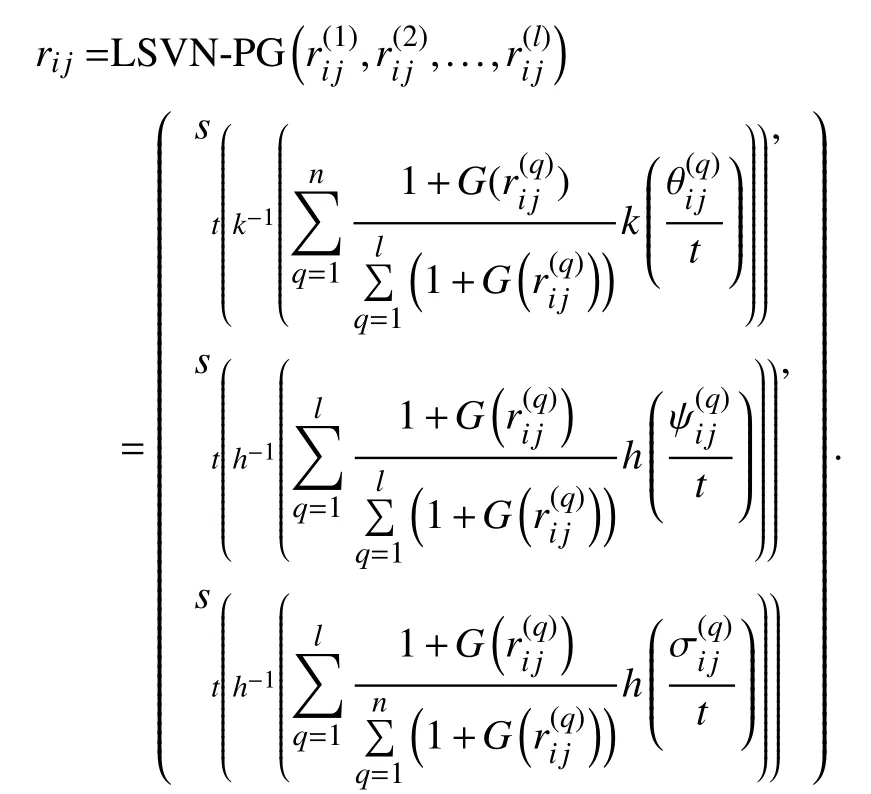
Step 3:Calculateas
where

Step 4:Calculate the comprehensive evaluation valueof each alternative by using LSVN-PWA or LSVN-POWA or LSVN-PHA or LSVN-PWG or LSVN-POWG or LSVN-PHG operator.
Step 5:Calculate the score functionby using Definition 3.
Step 6:Rank all the alternatives according to the descending order of score values of alternatives.
B. Illustrative Example
The above mentioned approach has been illustrated with a numerical example taken from Garg and Nancy [36] as:
Goods and services tax (GST) is one indirect tax for the whole nation, which will make India a unified common market. While GST promises to a user in an era of the unified indirect tax regime, integrating India into a single homogeneous market, it comes with certain complications inherited from the legacy tax regime. With the government gearing up to enforce the GST in Punjab from July 1, the issue of traders having limited computer knowledge and poor connectivity. In order to counter this, the state government has planned to train more than 2000 youths as“GST Mitra” to cater the traders. Punjab GST Mitra Scheme,which has to be started as a pilot project from Patiala, proposes to assist taxpayers in furnishing the details of outward supplies,inward supplies and returns, filing claims or refunds, filing any other applications etc., in GST Regime. It aims to create a group of Tax professionals available in the locality or at the doorstep of the taxpayer, at affordable costs throughout the State of Punjab.
The poor internet connectivity in far-flung areas has emerged as a big stumbling block in the success of “GST Mitra” scheme.In order to provide the online services to run this scheme, the state government is planning to give contract combinedly to private mobile service provider along with state-owned BSNL.For this purpose, committee formed by the government shortlisted the four internet service provider, namely, “Bharti Airtel”“ Reliance Communications”“ Vodafone India”and “Mahanagar Telecom Nigam”under the criteria:“Customer Services”“Bandwidth”“Package Deal”“Total Cost”with weight vector ω = (0.2, 0.3, 0.1, 0.4)T. Assume that weight vector associated with hybrid operator isGovernment has selected three decision makersandwho have the responsibilities to evaluate the given alternatives and rate their preferences in terms of linguistic term set Q = {s0= “extremely poor”,s1= “very poor”,s2= “poor” ,s3= “slightly poor”,s4=“fair”,s5= “slightly good”,s6= “good”,s7= “very good”,s8= “extremely good”}. The rating values of these decision makers are summarized as

Without loss of generality, we have taken the additive generatorand hence the following steps of the proposed approach have been summarized as
Step 1:By utilizing (11), we get


Step 2:Aggregate the values of the decision matrices by using either LSVN-PA or LSVN-PG operators and their results are summarized in Tables I and II respectively.

TABLE I Aggregated Matrix by Using LSVN-PA
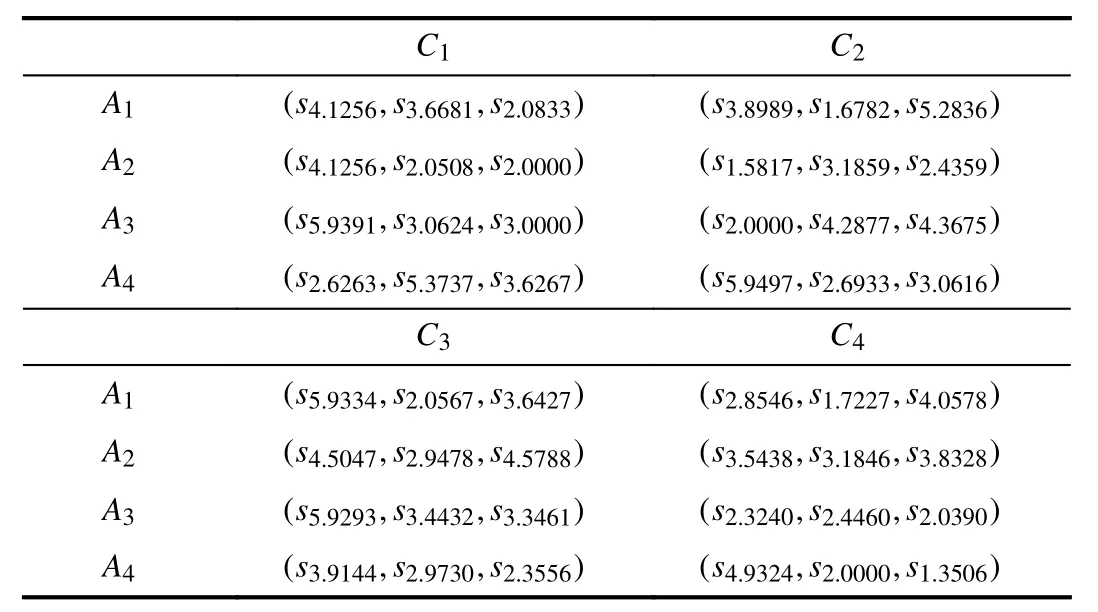
TABLE II Aggregated Matrix by Using LSVN-PG
Step 3:Compute
a) By using the data given in Table I, we have

b) By using the data given in Table II, we have

Step 4:By utilizing LSVN-PWA or LSVN-POWA or LSVN-PHA or LSVN-PWG or LSVN-POWG or LSVN-PHG operators, we get the aggregated valuesof the alternativesAi,i=1,2,3,4 and the results are summarized in Table III.

TABLE III Aggregated LSVNNS by Using Different Operators
Step 5:The score values of these aggregated numbers are summarized in Table IV.
Step 6:Based on these score values, the ranking order of the alternatives is summarized in the last column of the Table IV.From this table, we can see that corresponding to the different pairs, the best alternative is either
C. Comparative Analysis
To compare the performance of the proposed approach with the existing operators, namely linguistic neutrosophic number(LNN) weighted averaging and geometric aggregation operators denoted by LNNWAA and LNNWGA as proposed by Fang and Ye [35], LNN weighted power Heronian average(LNWPHA) proposed by Liuet al. [21] and Linguistic singlevalued neutrosophic Prioritized aggregation (LNPA) proposed by Garg and Nancy [36]. For it, the considered data of the problem has been taken and then the following steps of their approaches have been implemented which are summarized as follows:
Step 1:Aggregate the different preferences of decision makers by using LNNWAA or LNNWGA operators. The results of it are summarized in Tables V and VI respectively.On the other hand, if we apply LNWPHA operator (withto calculate the overall values of each alternative for each decision maker then their results are summarized in Table VII. On the other hand, the values of each alternative by LNPA operator are summarized in Table VIII.Step 2:Based on these aggregated values, the overall rating valuesof the alternatives are obtained by using LNNWAA areandwhile by using LNNWGA operator we getandHowever, by using LNWPHA operator to calculate the collective LSVN given in Table VII, we can getandBy LNPA operator, these values areand
Step 3:The score values and the final ranking of the alternatives are obtained by using values ofand results are represented in Table IX.
It is noted from this table that the best alternative obtained by the existing approaches is stillwhich coincides with the proposed approach. However, the computational procedure of the proposed approach is different from the existing studies. For instance, Fang and Ye [35] weighted averaging and geometric aggregation operators were introduced based on the algebraic sum and product and do not consider the dependency factor between the attributes. Liuet al. [21], they considered the PA and Heronian mean operator simultaneously to interact with the different pairs of LNNs. In [36], authors have aggregated the values by using prioritized aggregation operators. On the other hand, the proposed operator takes the advantages of LSVNS and power aggregation to aggregate the process by using the support function for solving MCGDM problems.
D. Further Discussion
To justify the importance of the proposed work with respect to the existing work, an investigation is done in the form of their characteristics comparison. The results are summarized in Table X.
The approaches in [16]–[18], [25] are based on a weighted averaging operators by utilizing the quantitative information only. Also, in their approaches, they had assumed that all the input arguments are independent of each other. Therefore, their approaches are limited and unable to apply to the linguistic information. However, on the contrary, the proposed approach can capture the interrelationship among input arguments and also describe for the qualitative with linguistic information.Hence, the present approach is much better than the methods in[16]–[18], [25]. In [35], authors have considered the linguistic features during the information extract phase and hence proposed the weighted averaging and geometric operators to aggregate them. But again, during their formulation, they assumed that all the collective information is independent of each other. Thus, their approach is limited. In [21] approach,authors have proposed power Heronian mean by utilizing the linguistic information by considering the interdependency between the pairs of the input arguments. Also, in [36], the authors have presented prioritized weighted operators for the linguistic SVNNs. However, the computational process in the proposed approach is entirely different from the existing one. In the proposed approach, the information used for the analysis is based on the linguistic nature which can reflect the inherent thoughts of decision makers more accurately. Also, the information about the attribute weights are extracted from the support measures instead of the priori assigned. In addition, it considers the interaction between the pair of the input arguments during the analysis.

TABLE IV Score Values of Aggregated LSVNNs

TABLE V Aggregated Matrix by Using LNNWAA
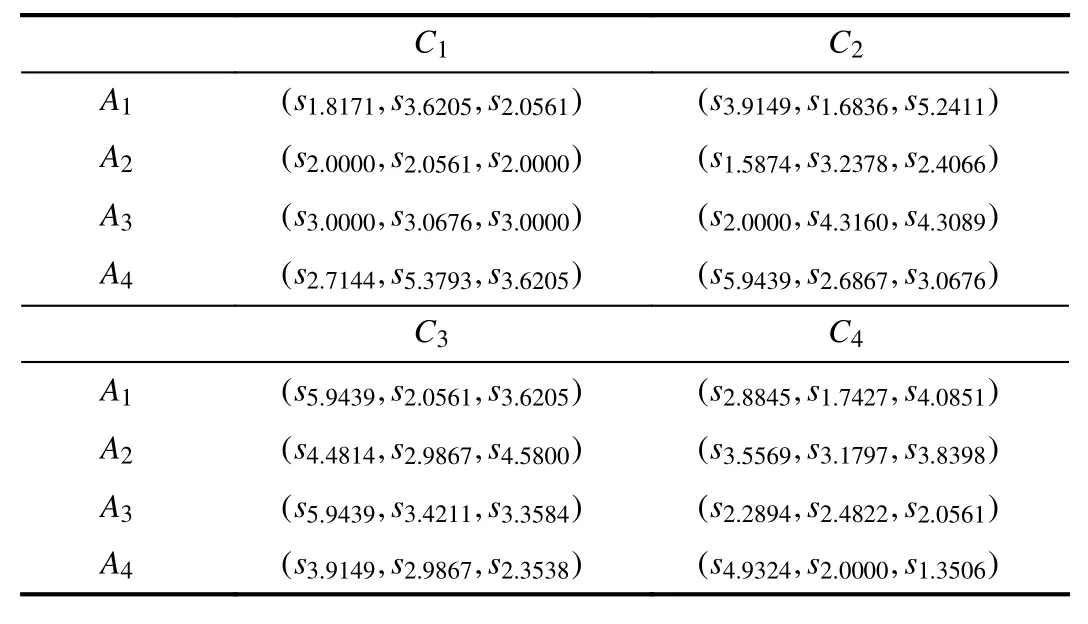
TABLE VI Aggregated Matrix by Using LNNWGA
E. Test Criteria for Evaluating the Decision-making Methods
To validate the proposed method, Wang and Triantaphyllou[6] gave some test criteria’s for validation of the decisionmaking approach which are given as follows:
Test criterion 1:“A valid decision-making approach should give the same best alternative even if a non-optimal alternative is changed by another worse one.”
Test criterion 2:“ An valid decision-making approach should have transitive property.”
Test criterion 3:“ Decomposition of decision-making problem into smaller problems should not affect the ranking of the original problem.”
To investigate the validity of the proposed approach, these three test criteria have been tested as follows.
1) Validity Under Criterion 1:As, it can be easily seen fromthe Table IV, the LSVN-PWA operator resultsas nonoptimal andas the worst one. For execution of the test Criteria 1 on the proposed approach, the alternativeis replaced with less desirable alternative in the original decision matrices. The changed data for the alternativeis given in Table XI.

TABLE VII Aggregated Values of the Alternatives by LNWPHA

TABLE VIII Aggregated Values of the Alternatives by LNPA
Apply the LSVN-PA operator to aggregate the modified decision-making metrics and then apply the LSVN-PWA operator to get the final aggregated values which are summarized asandThe score values of these numbers areand5.4918. Thus, alternatives are ranked aswhich indicatesis the best alternative as given by the actual problem. From this, we conclude that the given approach does not reverse the original decision after replacing the non-optimal alternative by some other alternative. Therefore, the proposed method is effective according to test Criteria 1.
2) Validity Under Criteria 2 and 3:For testing the validity of the above method by using the remaining two test criteria’s,we decompose the original problem into various smaller decision-making problems asandAfter applying the proposed approach, we get the ranking of decomposed decision-making problems asandrespectively. If we combine the ranking of these decomposed problems, we get the final ranking aswhich is same as that of the original (un-decomposed) problem and also performs the transitive property. Thus, both test criteria's verify the proposed approach.

TABLE IX Score and Ranking Values by Using the Existing Operators

TABLE X The Characteristic Comparisons of Different Methods

TABLE XI Rating of A3 for Each Decision Maker
V. Conclusion
In this paper, an attempt has been made to present the power aggregation operators from both arithmetic and geometric points of view, under the LSVN environment for various decision-making problems. The important characteristic of the proposed work is that they consider the supporting degree between the criteria’s and ignore the effect of biased assessments on the results by giving little importance to those false and biased ones compared to other ones. The proposed operators involve the simple power aggregation, power weighted aggregation, power ordered weighted aggregation,and power hybrid aggregation operators. These operators have been used to develop the group decision-making approach and then apply to a practical problem related to decision making.Further, from the comparative analysis and the validity tests,we can conclude that the proposed approach can be successfully utilized in evaluating the best alternative and is more reliable than simple algebraic and geometric operators as it considers the relationships among the criteria and overlooks the useless biased data. Future research will focus on introducing the various other operators [39]–[43] or to extend the approach to the linguistic interval neutrosophic environment [44]–[48].
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Artificial Intelligence Applications in the Development of Autonomous Vehicles: A Survey
- Data-Driven Based Fault Prognosis for Industrial Systems: A Concise Overview
- Review of Antiswing Control of Shipboard Cranes
- Research Progress of Parallel Control and Management
- Influence of Data Clouds Fusion From 3D Real-Time Vision System on Robotic Group Dead Reckoning in Unknown Terrain
- Effect of a Traffic Speed Based Cruise Control on an Electric Vehicle’s Performance and an Energy Consumption Model of an Electric Vehicle
