Fixed-time Sliding Mode Formation Control of AUVs Based on a Disturbance Observer

Zhenyu Gao and Ge Guo,

Abstract—In this paper, we investigate formation tracking control of autonomous underwater vehicles (AUVs) with model parameter uncertainties and external disturbances. The external disturbances due to the wind, waves, and ocean currents are combined with the model parameter uncertainties as a compound disturbance. Then a disturbance observer (DO) is introduced to estimate the compound disturbance, which can be achieved within a finite time independent of the initial estimation error. Based on a DO, a novel fixed-time sliding control scheme is developed, by which the follower vehicle can track the leader vehicle with all the states globally stabilized within a given settling time. The effectiveness and performance of the method are demonstrated by numerical simulations.

I. Introduction

DURING the past decades, considerable attention has been paid to the coordination control of multi-autonomous underwater vehicles (AUVs) system [1]–[6] owing to various applications, such as ocean sampling, mapping and ocean floor survey. A typical control problem is formation control, which focus on designing a control law for the follower AUV to make the vehicle reach and follow the leader with a given geometrical configuration. In recent years, many outstanding results on formation problem have been presented [7]–[11].

In the formation control of AUVs, an important performance index of the control strategy is the convergence speed.Most of the existing literature only guarantee asymptotic convergence of the tracking errors, which means the formation task can only be achieved as time approaches infinity [8], [9]. Clearly, it would be a great advance if AUVs can construct a given configuration in finite time. Fortunately,some new results on coordinated control of various nonlinear systems were proposed in recent years [12]–[15]. They use the notion of fixed-time stability [16] which focus on designing coordination control laws with guaranteed settling time regardless of the initial conditions of the agents. Although the idea of fixed-time formation control is promising, research works so far have been focused solely on the consensus problem of general multi-agent systems with various dynamics, although a fixed-time formation tracking problem was studied for AUVs without taking model parameter uncertainties and external disturbances into account. The aim of this paper is to find a fixed-time control solution to a multi-AUVs formation problem.

Due to the nonlinear nature of the AUV and because it is easy effected by external disturbances, it is very difficult to generalize existing results for second-order integrator systems[12]–[14] to multi-AUVs system with more complex dynamics. In this work, we further consider the fixed-time formation tracking problem for multi-AUVs systems with model parameter uncertainties and unknown external disturbances. In terms of model parameter uncertainties or external disturbances, there are mainly two types of solutions:approximated value-based control [1], [8], and observer-based control [17]. In the approximated value-based approach [1],[8], the parameter uncertainties and external disturbances are estimated by neural networks. Due to reconstruction residuals,the neural networks (NNs)-based method can only make tracking errors globally uniformly ultimately bounded(GUUB), rather than asymptotically stable. Using a nonlinear observer to precisely estimate external disturbances acting on underwater vehicles is another alternative solution in dealing with disturbances [17], in which an unknown external disturbance was estimated by a disturbance observer, but the effect of the model parameter uncertainties was missed.

In this paper, we develop a fixed-time protocol for the formation of AUVs in the presence of model parameter uncertainties and external disturbances. The main contributions of this paper are stated as follows: 1) By combining the model parameter uncertainty and external disturbance as a compound disturbance, a disturbance observer is present, which can estimate a disturbance exactly within a fixed time independent of the initial estimation errors.2) Under the disturbance observer (DO) and in the framework of fixed-time sliding mode control, a fixed-time formation tracking control method is proposed, which can guarantee global fixed-time stability of the formation system.

The organization of this paper is as follows. Graph theory and some useful preliminaries are presented in Section II.Section III presents the system modeling and problem formulation. Section IV presents the main results. Section V simulates the proposed control approach, and finally, we conclude this paper in Section VI.

Notations:The following notations are used throughout this paper. Denotesgn(x), whereand sgn(·)is the standard sign function. For a vectorthe Euclidean norm ofis denoted as

II. Graph Theory and Preliminaries

A. Graph Theory

B. Preliminaries

In this subsection, some definitions and lemmas are reviewed, which will be useful for the subsequent analysis.

Consider a nonlinear system

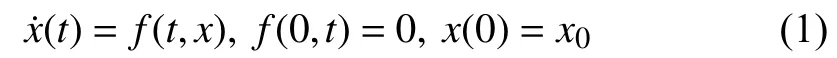
Definition 1 [16] :The origin of the system (1) is said to be globally finite-time stable if it is globally asymptotically stable and any solutionof (1) reaches the equilibria at some finite time moment, i.e.,whereis the settling-time function.

Definition 2 [16] :The origin of system (1) is said to be globally fixed-time stable if it is globally uniformly finite-time stable and the settling time functionis globally bounded,i.e., there exists a finite constantsuch thatandfor alland

Lemma 1 [16] :For system (1), if there exists a continuous radially unbounded functionsuch that

Then, the system trajectoryis globally fixed-time stable,and the settling timeIfthen it is globally fixed-time stable with settling timebounded by

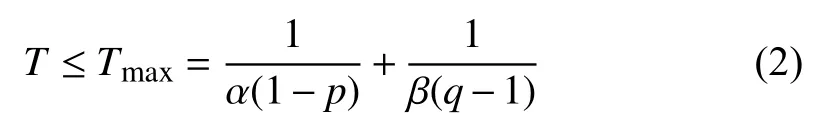
Lemma 2 [16] :For system (1), if there exists a continuous radially unbounded functionsuch that

Then, the practical fixed-time stable can be achieved.Moreover, the residual set of the solution of system can be given by

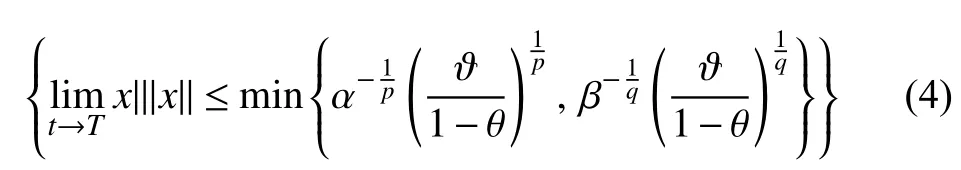
Lemma 3 [18] :Consider theintegrator system

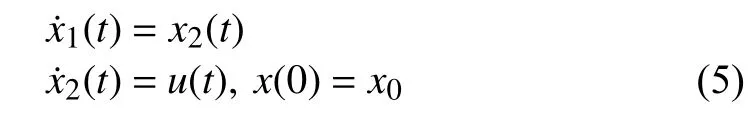
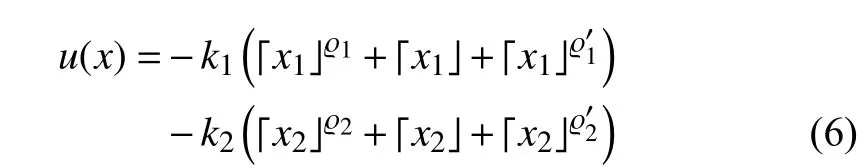
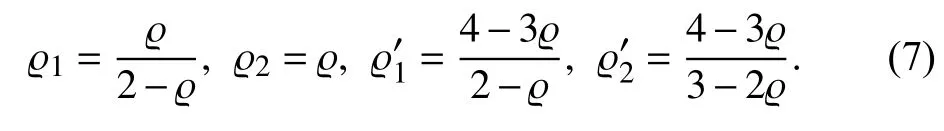
III. System Modeling and Problem Formulation

In this section, the system modeling of AUVs, which consists of the vehicle kinematic and dynamic subsystems, is conducted. Then, based on the constructed system model, the main control problem considered in this paper is addressed.

A. AUV Dynamics

Consider a multi-AUVs system consisting ofAUVs with nonlinear uncertain dynamics modeled as [19]

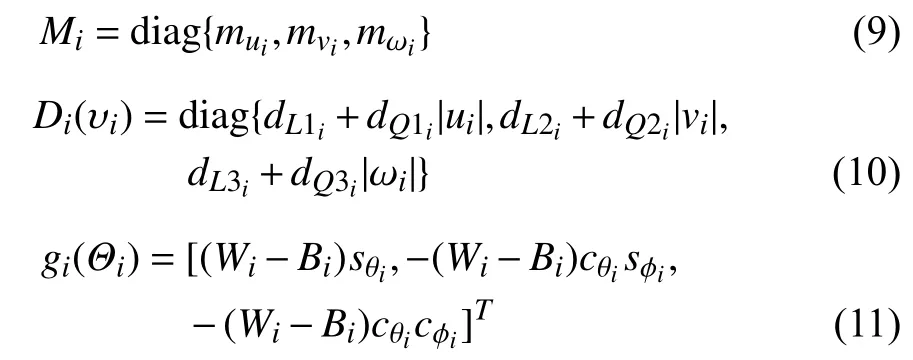
For simplicity, the dynamics model (i.e., the second part in(8)) can be rewritten as:

Assumption 1 [20] :Assuming that the following expression satisfies

Remark 1:The nonlinear termis velocity-related function, and it is natural to assume that their derivatives are bounded by velocity-related functions. Furthermore, the energy of external disturbances is limited, so after the above analysis, Assumption 1 is reasonable.

Assumption 2:In the multi-AUVs system (8), the leader is globally reachable.

B. Problem Statement

In this paper, we consider an interesting scenario in which thefollower vehicles can each independently follow the global leader AUV. Namely, the entire formation can be decomposed intosubformations, each of which comprises a follower AUV and the global leader, as shown in Fig. 1. In each subformation, the followertries to maintain a desired distancerelative to the global leader. Without loss of generality, the objective here can be described as designing a control lawfor a followerso thatand the leader AUV can achieve a formation given in the global coordinate frameNamely, the distance between the leader AUV and the followerreaches a desired value in finite time, i.e.,

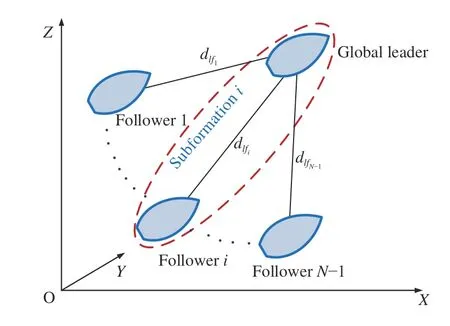
Fig. 1. Leader-follower configuration of multi-AUVs formation system.

As described above, all AUVs have fixed attitudes. This means that each member of the subformation has the same velocity when the formation goal is achieved. So the objective in this paper also can be described as

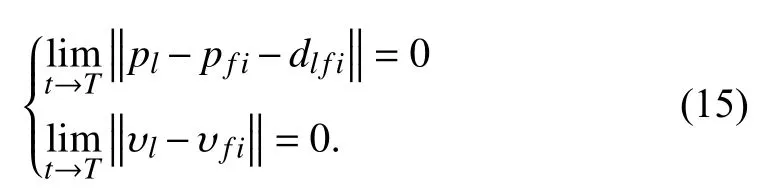
IV. Main Results

In this section, firstly, a fixed-time based disturbance observer is designed to estimate the compound disturbancethen, based on the observer, a novel fixed-time formation control protocol is proposed to achieve the control objective(i.e., (14) or (15)).

A. A Fixed-time Disturbance Observer

As described in Assumption 1,cannot be measured directly, so a DO is designed to estimate its actual value.

Taking the time derivative ofone obtains

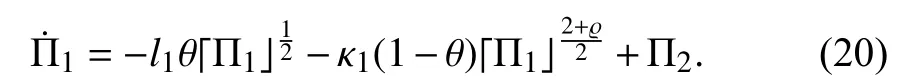
Taking the time derivative ofyields

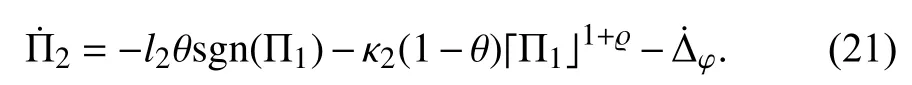
As a result, the estimated error dynamics of the observer foris

According to the above contents, the main result is summarized as the following theorem.Theorem 1:Using the observer (16) under Assumption 1,the compound disturbance termcan be estimated precisely within a fixed timeupper bounded by a constant

independent of initial estimation error.

Proof:A detailed proof of the theorem can be seen in [22].■

Remark 2:Different from the existing disturbance observers, in this paper, the external disturbances and model parameter uncertainties are considered as a compound disturbance termand the proposed fixed-time DO can achieve exact estimation within a finite time upper bounded by a positive constant independent of initial estimation error.

Remark 3:The upper bound of the settling time only depends on the designed parametersandThis implies that the settling time can be tuned only by adjusting parameters to satisfy the requirement of the convergence time, which greatly improves its application in practice.

B. Formation Tracking Control

In this section, a new fixed-time formation control protocol is given.

Define the position tracking errorand velocity tracking erroras follows:

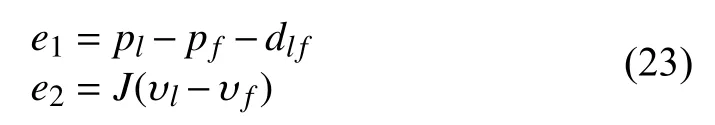
and, the dynamics of system (23) is

Substituting the dynamics model (8) and (13) into (24), we have

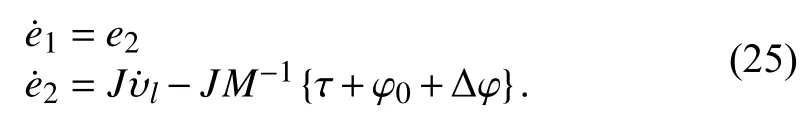
To solve the fixed-time formation tracking problem, the following integral sliding surface for each follower AUV is proposed:

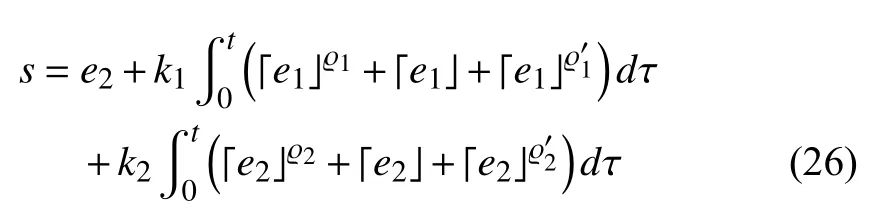
In view of (27), a new fixed-time formation tracking control protocol can be prescribed as follows:

Substituting (28) into (27), one obtains

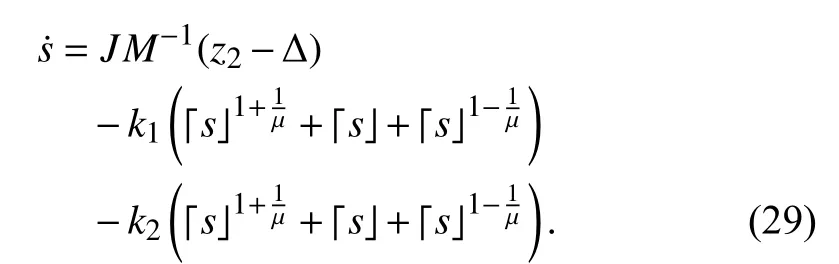
The main result in this section is summarized as the following theorem.

Theorem 2:Consider a multi-AUVs formation system (8). If Assumptions 1 and 2 holds, the fixed-time formation tracking control objective (i.e., (14) or (15)) can be achieved by the given control protocol (28) under the disturbance observer(16).

Proof:Consider the candidate Lyapunov function as follows:

Taking the time derivative ofyields

where

Substituting (28) into (31), we have

The designed observer guarantees the estimation errorconverges to zero in fixed time which implies thatis bounded. Therefore, it can be concluded thatwill not go to infinity before the convergence of the observer error dynamics.

In the light of Lemma 1, we find that the system trajectory will reach the sliding surfacein a fixed settling time and the settling timeSinceapproach to zero in fixed time, (29) can be rewritten as

which is fixed-time stable.

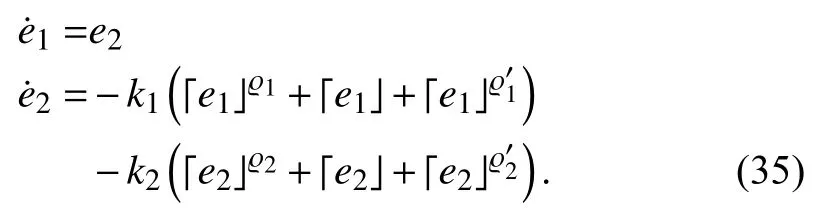
It follows from Lemma 1 that the tracking error dynamics(35) are fixed time stable at the origin, i.e., there exists a constantindependent of initial conditions such that the formation tracking errorconverges to zero fort≤To+Tr+Ts. ■

Remark 4:Our protocol is different from existing control protocols in [7]–[9] which the controller is designed by two steps. In step 1, the virtual velocity is designed to achieve formation control with use of kinematic, and the actual control input (i.e., force or torque) is designed to achieve formation control of multi-AUVs with use of dynamics in next step. The proposed control protocol in this paper is designed in one step,which is similar to consensus control of a multi-agent system.

V. Simulation

In this section, numerical simulation examples are provided to illustrate the effectiveness of the proposed fixed-time control protocol (28) with a designed fixed-time disturbance observer (22) for formation control of five autonomous underwater vehicles. Fig. 2 shows the communication topology. Simulations are carried out using MATLAB/Simulink environment.

Fig. 2. Communication topology of the multi-AUVs system.

For the sake of simplicity, we assume that the uncertain termonly comes from external disturbances, and we define the disturbanceas time-varying forces/moment in framewhich can be described as follows:

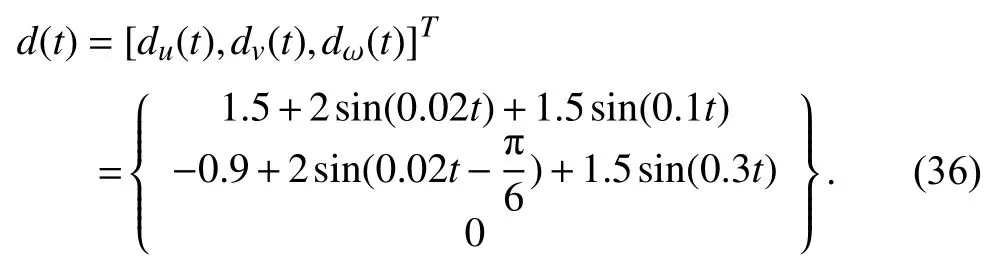
Here, it is assumed that the dynamics of the AUVs is identical and all AUVs have the same structure and the model parameters are100+and

The trajectory of leader AUV is described as follows:

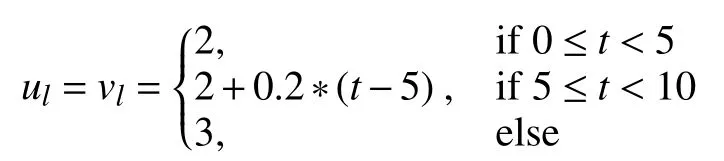
and

The formation of multi-AUVs is placed in the global coordinate framewhere the desired relative distance among theis given bywith the initial positionand the initial velocity(i=1,2,3,4).

In the simulations, the parameters in (26) and (28) are taken asandThe parameters of the observer are chosen asand

The trajectory of each AUV is shown in Fig. 3, which indicates the follower AUVs follows the leader AUV in the desired formation configuration well with the designed control law. As shown in Fig. 4, the position tracking errorsof the AUVs are converging to zero. It is illustrated that the follower AUV trajectory can track the leader AUV trajectory at a good precision around 3 seconds, which approximates the settling time determined by the chosen parameters. Fig. 5 shows the velocity of the follower AUV, where it can be seen that the velocity of the follower AUVs is the same as that of the leader AUV when the formation is implemented. Fig. 6 shows that the unknown disturbances can be estimated within a finite time by the proposed observer. In the end, the actual control forceandare shown in Fig. 7.

From the simulation results, it can be observed that all signals are bounded, and tracking performance can be achieved. The convergence time satisfies the relational expressionas expected.

VI. Conclusion

The fixed-time formation control problem of multi-AUVs with model parameter uncertainties and external disturbances has been addressed in this paper. Firstly, a fixed-time DO is designed to estimate the compound disturbance induced by model parameter uncertainties and external disturbances.Then, a new control protocol, based on the designed observer,is developed, which ensures that formation control can be achieved within the settling time, while guaranteeing all signals of the closed-loop system are globally fixed-time stable. Simulation results demonstrate the effectiveness of the proposed control protocol.

Fig. 3. The trajectory of each AUV in the multi-AUVs system.

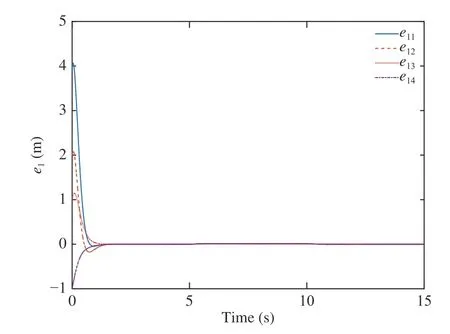
Fig. 4. Position tracking error between the leader AUV and follower in a multi-AUVs system.

Fig. 5. Velocity of each follower AUV in the multi-AUVs system.

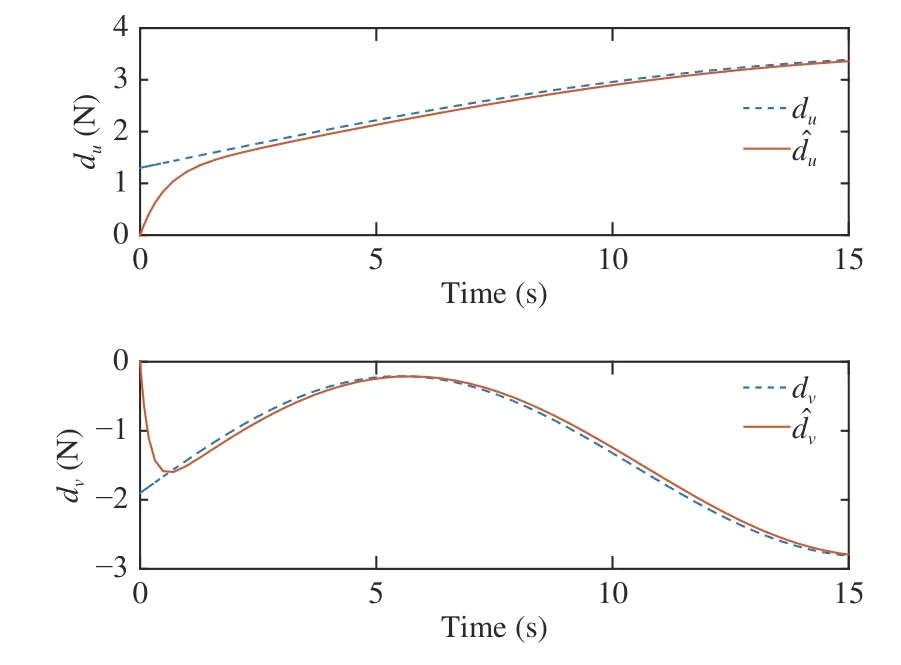
Fig. 6. Disturbances and their estimates

Fig. 7. Control forces and of each follower AUVs.

Future research will focus on the extension of the research results to multi-AUVs with bounded yet unknown uncertainty.