Estimating oak forest parameters in the western mountains of Iran using satellite-based vegetation indices

Adel Nouri · Bahman Kiani · Mohammad Hossein Hakimi ·Mohammad Hossein Mokhtari

Abstract Remote sensing is an important tool for studying and modeling forest stands. Vegetation indices obtained from Landsat-8 remotely sensed data were used to estimate the forest parameters in the western mountains of Iran. Thirtyfour sample points were selected on the map of Bayangan County,Kermanshahprovince,Iran.Ateachpoint,aclusterof five rectangular plots of 8100 m2 and 200 m apart was established. Some clusters were primarily sampled to determine the variance of the forest parameters. The coefficient of variation was used as a criterion for sample allocation. Stand density, canopy cover and basal area per hectare were calculated for each plot. Vegetation indices were extracted from the Landsat-8 images for each plot. Simple linear and nonlinear regressions were conducted to develop the models. The models were validated using an independent data set. Stability of model parameters was statistically evaluated. The results showed that Normalized difference vegetation index (NDVI)and Transformed normalized difference vegetation index (TNDVI) followed by Simple ratio vegetation index(SRVI) were the best predictors, explaining up to 91% of the variations with high precision. For NDVI, Soil adjusted vegetation index 2 (SAVI2) and SRVI, the cubic model was more appropriate than the linear model for predicting the forest parameters. For this model, the R-square value increased while NRMSE decreased significantly. For Infrared percentage vegetation index (IPVI), the quadratic model was better,but, for other vegetation indices, nonlinear models were not superior to linear ones. Finally, it can be concluded that Landsat-8 imagery is suitable for predicting forest parameters in the oak forests of western Iran. Of course, large plots must beselected,andpre-classificationisnecessarytogainaccurate and precise estimations.

Keywords Basal area · Canopy cover · Density ·Landsat-8 · Modeling

Introduction

Due to their fragile ecosystem, natural forests might not be properly managed unless forest parameters are accurately estimated. Forest sampling through fieldwork is very difficult and costly, and for noncommercial forests of developing countries, budgets for sampling may not be adequate.Researchers, therefore, seek low-cost methods to predict forest parameters (Delpasand et al. 2014; Liang et al.2016). Recently, up-to-date and high-quality data on forest areas have been provided through remote sensing.Employing appropriate techniques for image processing makes it possible for researchers to achieve robust models to predict forest parameters (Tian et al. 2014). Of course,taking enough samples and using the appropriate shape,space and location for sample plots in the forest area are very important (Fassnacht et al. 2014). The Landsat-8 satellite, launched in 2013, has made it possible for researchers to continuously gain data using the onboard Operational Land Manager (OLI) and Thermal Infrared Sensor (TIRS) instruments (Roy et al. 2014). The spatial resolution of the satellite images was medium (15-100 m).In addition, by creating less noise in radiometric functions,the satellite, compared to previous Landsat generations such as TM and ETM, provides a better distinction for plant vegetation (Irons et al. 2012). The Landsat 8 panchromatic band, compared to previous sensors, has a narrower bandpass, providing greater contrast between vegetated and bare surfaces. Moreover, the Landsat 8 data set with 12-bit quantization has a higher signal-to-noise ratio in comparison with the previous 8-bit old generation of Landsat 7 and Landsat 5 data sets (USGS 2016). Generally, a data set with a higher radiometric resolution is expected to be more useful for dealing with the reflected energy and estimating vegetation parameters.

Although Landsat images have a medium resolution, they have always been used for forest modeling for various reasons suchasimagingreliability,appropriatetime coverageandfree of cost (Woodcock et al. 2008). They have been helpful especially because empirical models can be developed using them. Many studies have focused on the application of Landsat images to predict forest parameters (McRoberts et al.2010; Abdollahnejad et al. 2018; Wilson et al. 2018). However, in previous studies, classification has not been consideredasanimportantissue,andmayhavebeenthecause forthe emergence of models with low accuracy and predictability. In those studies, the plot area often does not seem proportional to the pixel size in Landsat images. For example, in a study to estimate forestdensity in the central forests of Iran, Delpasand et al. (2014) found that the infrared percentage vegetation index (IPVI) was the best predictor of stand density, but the coefficient of determination was low (R2= 0.27).

In a study of the Hyrcanian forests of Iran using Landsat 8 data, Renoud et al. (2015) reported that the infrared band was not suitable for predicting stand basal area (R2= 0.16).Trying to predict the biomass and carbon storage of Indian forests, Watham et al. (2016) concluded that Landsat data are not suitable because forest biomass seems to be highly variable at short distances. Gunlu et al. (2012) indicated that Landsat TM data can explain half of the variation in the stand volume of Abies bornmuelleriana forests in Turkey. It can be seen that the value of the coefficient of determination in many studies is not satisfactory. Sometimes, the accuracy of the model is low. For example, when Landsat-8 images were used to create canopy and biomass maps, 77% of the variation in forest canopy and 57% of the variation in stand biomass was explained by RMSEs of 40% and 66%, respectively (Karlson et al. 2015). In addition, Mohammadi et al. (2011) reported R2= 0.73 for predicting stand density in northern forests of Iran. They used ETM+data, but model precision was low.Considering forest heterogeneity in terms of density and canopy in the western mountains, classification before sampling and choosing large plots seem to be necessary.Therefore, in the present study, we sought to overcome these issues by pre-classifying satellite imagery and choosing larger plots.

Gizachew et al. (2016) precisely predicted forest biomass and carbon sequestration in woodlands using satellite imagery. Moreover, Watt et al. (2004) found a significant correlation between stand height and ground measurement(R2= 0.84), consistent with the results obtained from IKONOSimages.Hudaketal.(2005)comparedLandsat and Lidar data to predict forest density and the basal area. They concluded that Landsat data can explain from 80 to 93% of the variations in forest parameters. Logarithmic and square transformation improved model performance. In the oak forests of Iberia, NDVI and the atmospherically resistant vegetation index (ARVI) derived from Landsat TM explained more than 70% of the variation in the stand canopy (Carreiras et al. 2006). Sivanpillai et al.(2005) preferred Landsat ETM+data to determine the forest cover on a national scale. In another study, Khorrami et al. (2008) found that 60% of the variationinthestandvolumecouldbeexplainedbyETMdata.In addition, in a study by Gunlu et al. (2014), the enhanced vegetation index (EVI) explained 60% of the variation in the biomass of Anatolian pine forests. The researchers concluded that vegetation indices are better than single bands.

Toward improving modeling forest parameters using satellite data, in the present study, we used Landsat-8 images to calculate vegetation indices and estimate the density, canopy cover and basal area of the oak forests of the Bayangan Mountains in western Iran.

Materials and methods

Site description

This study was conducted in Bayangan County, Kermanshah Province, Iran (longitude 46°00′20.19′′-46°24′18.34′′, latitude 34°57′20.44′′-35°04′38.19′′; elevation 1250-2500 m a.s.l.)(Fig. 1). The average precipitation in the study area is 579 mm,and the mean annual temperature is 12 °C. The tree species mainly include Quercus brantii (Lindl), Acer monspessulanum subsp. cinerascens Boiss., Pistacia atlantica Desf., Pyrus glabra Boiss. and Crataegus aronia L. (Safari et al. 2010).

Methods

Fig. 1 Location of the study area in Bayangan district in northern Kermanshah Province, a mountainous area in western Iran

In the study area, four strata were denoted according to the NDVI of the Landsat-8 data set. In each stratum, four sample points were randomly determined, and a cluster including five plots was characterized. The area of the plots was 200 m2, and they were spaced out at the distance of 200 m. The number of trees, the diameter at the breast height and the crown width were measured and recorded for all the sampling plots. Finally, the stand density, the canopy cover and the basal area were calculated. The sample size was determined using Eq. (1) and allocated to each stratum and Eq. (2), respectively (Kiani 2017):

where n is the required sample size, E is the acceptable sampling error (E = 10%), T is the value of the Student’s t-table (for df = n - 1), CVtis the total variation coefficient (sum of CVs of three strata), njis the computed sample size for stratum j, and CVjis the variation coefficient in stratum j determined in the primary sampling.According to Eqs. (1) and (2), 12 clusters including 60 sample plots in stratum II, 40 clusters including 70 sample plots in stratum III and eight clusters including 40 sample plots in stratum IV were determined and measured (stratum I was covered with bare soil and consequently excluded from sampling).

For reducing the effect of soil reflection, a soil line was determined using the scatterplot of NIR and RED bands.To do this, 30 sample points were randomly determined on the soil stratum. The points were specified on the images to determine the corresponding spectral values. Linear regression was conducted between the red and infrared bands (Akdim et al. 2014). The scatterplot of this relationship (Fig. 2) shows that soil reflectance is a straight line, from which vegetation begins. In addition, α is the slope and β is the intercept of the soil line. A soil line is used to normalize the soil background effect for vegetation discrimination. Some vegetation indices are designed based on the soil line to minimalize the soil background effect.The line is also useful for estimating fraction cover, vegetation residual cover, soil organic matter and soil degradation. Since a soil line is relatively stable for a certain soil type, it can be applied as a transformation method to perform relative atmospheric corrections (Xu and Guo 2013).

Fig. 2 Scatterplot and equation of the soil line based on Red and NIR bands

Since various vegetation indices are responsible for different environmental conditions (Hatfield and Prueger 2010) such as plant density, background soil and atmospheric conditions (Barati et al. 2011), a part of this study was dedicated to investigating the ability of a set of vegetation indices, as mentioned in Table 1, to estimate forest parameters. These indices were calculated based on Landsat red and near-infrared (NIR) bands (Table 1).Bands 4 and 5 of the Landsat satellite, respectively, measure red rays and near infrared rays, which are important for vegetation studies. Red light is strongly absorbed by healthy vegetation, whereas NIR is reflected. Broad-leaved trees and conifer trees differ in terms of their reflectivity rate, and the difference is greater for NIR than for red light.A comparison of NIR with other bands provides vegetation indices such as NDVI, which allow researchers to estimate plant health more precisely (Myers and Patil 2006).

My dear sir, replied the old man, my stock in trade is not very large-I don t deal in laxatives and teething mixtures-but such as it is, it is varied2. I think nothing I sell has effects which could be precisely3 described as ordinary.

Two main classes of vegetation indices were used in this study (Table 1). The first class included WDVI, PVI, SAVI and SAVI2 as soil-line-dependent indices. The main reason for using the distance-based vegetation indices was to cancel the effect of soil brightness in cases where vegetation is sparse and pixels contain a mixture of green vegetation and soil background and is particularly important in arid and semi-arid environments. Distance-based vegetation indices require the slope (α) and the intercept (β) of the line as input for the calculation. The second class included NDVI, TNDVI, SRVI, DVI, TVI, RDVI and IPVI as soilline independent indices (Ramachandra 2007).

For each plot, the vegetation index value was calculated.Then, linear regression and curve estimation were conducted to create simple linear and nonlinear models. For nonlinear models, the evaluated regression assumptions included normality, independence and random distribution of residuals, the linear relationship between the target and predictor variables, and lack of outliers. The curve estimation was done to fit the quadratic, cubic, logarithmic,inverse, logistic, power and exponential models on the data. To test the significance of the R2change between t simple and multiple models (quadratic and cubic), we used an F test (Eq. 3) as follows (Kiani 2015):

where F is the test statistic, N is the sample size, KLis the number of independent variables in the larger model, KSis the number of independent variables in the smaller model,andandare the coefficients of determination for the larger and the smaller model, respectively. The degree of freedom of the numerator is KL- KSwhile that of the denominator is N - KL- 1. If the calculated F is greater than the tabulated F, the null hypothesis is rejected, and the R2change is considered significant. Using the FDIST function in Microsoft Excel, we can obtain the p value.

Following the method of Shcherbakov et al. (2013), the models were compared using the coefficient of determination (R2) as a criterion for evaluating predictive ability and the normalized root mean square error (NRMSE) as a criterion for evaluating precision (Eq. 4):

Table 1 Vegetation indices used in this study

where NRMSE is the normalized root mean square error, ^Yiis the estimated value of the dependent variable, Yiis the observed value of the dependent variable, Ymaxis the maximum value of the dependent variable, and Yminis the minimum value of the dependent variable. The stability of the model parameters was tested by using an independent data set (from primary sampling) and comparing the models fitted on the training data set (170 plots) with the test data set (30 plots) as recommended by Weaver and Weunsch (2013).

Results

The descriptive statistics of the forest parameters are presented in Table 2. For all the variables, the sampling error was lower than 10%, an acceptable value (Skidmore et al.2015). The mean stand density was 221.83 trees ha-1, the mean canopy cover was 2013.51 m2ha-1, and the mean basal area was 4.77 m2ha-1.

To identify the appropriate variables to be included in the regression models, we first did a correlation analysis.The results are presented in Table 3.

The scatterplots of the relationships between the aforementioned parameters and NDVI are in Fig. 3. There were linear relationships between vegetation indices and forest parameters. Of course, this figure presents only the NDVI scatterplots.

The results of the simple linear regression showed that a significant correlation between the predictors and the stand parameters. The vegetation indices explained 58-91% of the variations in the forest parameters with the NRMSEs of 9.03-23.84%. The linear models can be seen in Table 4.

The results showed that NDVI and TNDVI followed by SRVI were the best predictors of stand density(R2= 0.85-0.86, NRMSE = 11.23-11.88%), stand canopy cover (R2= 0.82-0.83, NRMSE = 11.06-11.51%) and the stand basal area (R2= 0.81-0.82, NRMSE = 10.9%-11.27%). The zoning map of the forest parameters, predicted based on the NDVI index, can be seen in Figs. 4 and 5. Of course, due to the high correlation between density and canopy cover, the two maps look like each other. As mentioned earlier, NDVI was the best explanatory variable for predicting and modeling the forest parameters in the study area.

Due to the excessive volume of the model validation results, the results of the cross-validation process are shown only for the NDVI index (Table 5). For all models,the stability of R2and the model parameters were confirmed.

As the statistical analysis showed, there was no significant difference between the trained model and the model fitted on the test data set in terms of the constant value and the regression slope (Table 6). The amount of the p value for the categorical variable Group implied no significant difference between the two constants. In the same way, the amount of the p value for the interaction effect implied no significant difference between the two slopes.

Figure 6 shows the overlaid scatterplot of the relationship between NDVI and forest parameters for trained and test data sets. As can be seen, there is good coincidence between the models fitted on the two data sets.

To ensure the goodness of fit for the nonlinear models, a curve estimation analysis was conducted for NDVI as the best predictor in the linear models. The results showed that the cubic model gave a better fit than the linear model for predicting forest density. The R2value increased from 0.86 to 0.91, but NRMSE decreased from 11.23 to 9.03 for this model (Table 7). The R2change was significant only for the cubic model (F = 46.11, p value = 0.000). The quadratic model was not suitable for predicting forest density and canopy cover. The power model had a slightly more predictive ability but less precision.

Similar results were obtained for predicting forest canopy cover; the cubic model had a better fit than the linear model. R2increased from 0.83 to 0.88, but NRMSE decreased from 11.04 to 9.46 for this model (Table 8). The R2change was significant only for the cubic model(F = 34.58, p = 0.000).

Table 2 Descriptive statistics of the target variables

Table 3 Correlations between the vegetation indices and stand characteristics

Fig. 3 Scatterplots of the relationship between NDVI and the target variables

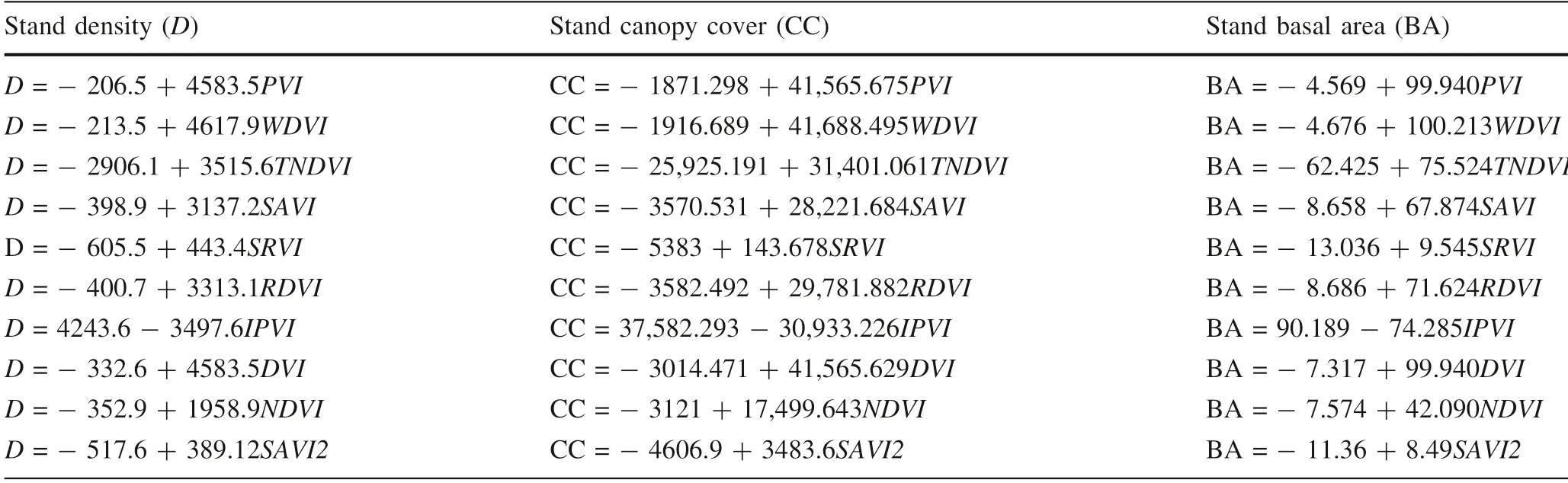
Table 4 Linear models used to predict the stand parameters

The cubic model was the best model for predicting the stand basal area. R2increased from 0.82 to 0.85, but NRMSE decreased from 10.90 to 9.86 for this model(Table 9). The R2change was significant only for the cubic model (F = 16.61, p = 0.000).

The nonlinear models were fitted and compared to the linear ones for predicting forest parameters using other vegetation indices. The results showed that the linear models were preferable in most cases (Table 10). The cubic model was a better fit for the SRVI, SAVI2 and NDVI data. Moreover, the quadratic model was preferable for IPVI because the R2increased and NRMSE decreased.

Discussion

The use of satellite images to generate robust models has been of great interest for predicting forest parameters,especially in non-commercial forests, where a large field survey is not practical. Owing to the functions of different vegetation indices in various spatial and environmental conditions, several classes of indices have been used to model the forest parameters. In the current study, some linear models with noticeable predictive ability and precision were reached. The corresponding vegetation indices explained up to 91% of the variation in the stand density, incontrast to the results obtained by Pirbavaghar (2011) using IRS-P6 data, which predicted only 31% of the variation in the stand density of the western forests of Iran. They also predicted only 42% of the variation in the stand basal area,while we predicted 85% of the variation in the stand basal area.

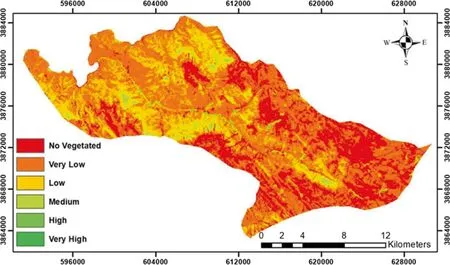
Fig. 4 Density map predicted by the NDVI linear model

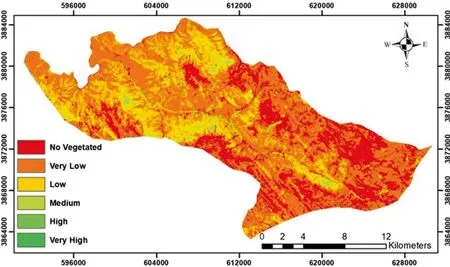
Fig. 5 Canopy cover map predicted by NDVI in the linear model

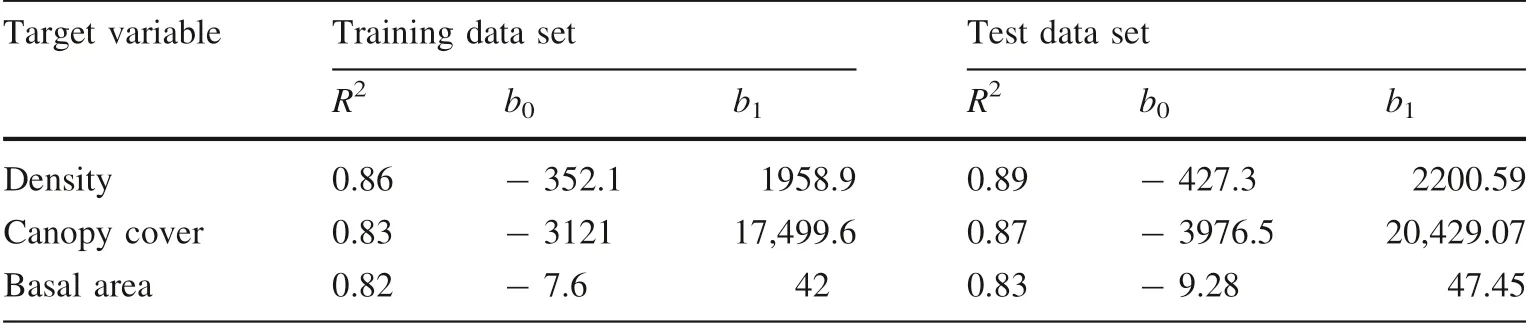
Table 5 Results of the linear model cross-validation for NDVI

The precision of the models in our study was better than in other studies that used Landsat data. Apparently, the preclassification of the forests and the use of wide plot areas(90 × 90 m) had a significant effect on the results. We note that a universal model may not be suitable for predicting forest parameters, where forest density and canopy cover are spatially variable, as indicated previously byothers such as Barati et al. (2011) and Delpasand et al.(2014). In a study by Mohammadi et al. (2011), DVI and greenness indices were found to be suitable predictors for predicting stand density using a bivariate model(R2= 0.73). In our study, however, DVI was more precise;it predicted 57% of stand density variation with NRMSE = 19.9, while the bivariate model was not significant.

Table 6 Results of the general linear regression for the crossvalidation of the NDVI model

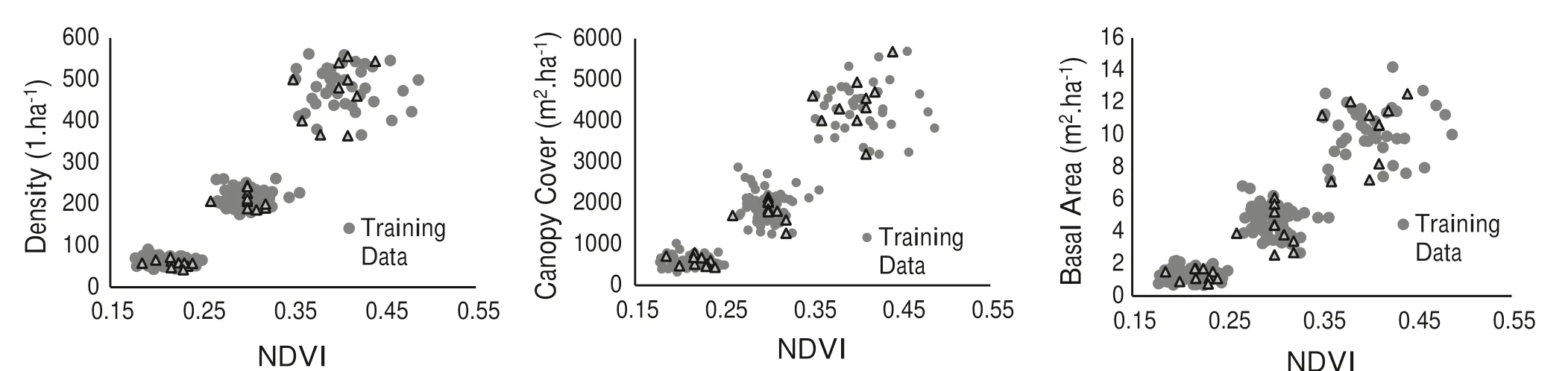
Fig. 6 Scatterplots of the training and test data sets to validate the models

Table 7 Linear and nonlinear models for predicting density

According to Delpasand et al. (2014), the best predictor of the stand density of P. atlantica and Amygdales scopariaforests in the Iranian central forests is IPVI. The low R2was associated with the low density and canopy cover of the trees and the effect of the herbaceous layer. The uneven distribution of plots across the area, the scant plot size(1000 m2) and severe variability in vegetation also seemed to have a significant effect. However, our study showed that the R2was 0.55 for IPVI due to the large plots(8100 m2) and pre-classification. Of course, the R2for this index is still not satisfactory, so IPVI is not a suitable predictor of stand density.

Table 8 Comparison of the linear and nonlinear models for predicting canopy cove

Table 9 Linear and nonlinear models for predicting the basal area

Table 10 Precision and predictive ability of linear and nonlinear models

A study by Carreiras et al. (2006) showed that NDVI and ARVI could predict about 70% of the variation in the canopy cover of the evergreen oak forests of Portugal. In our study, NDVI was a suitable predictor of stand canopy cover with R2= 0.83 and NRMSE = 11.06% in the linear model and R2= 0.88 and NRMSE = 9.5% in the cubic model. Moreover, SRVI predicted canopy cover with R2= 0.82 and NRMSE = 11.5%. The results indicated that the performance of the TNDVI index was the same as that of the NDVI index. Since the crowns of the plant species in the study area had a rather horizontal development, vertical density did not cause saturation; hence, the NDVI-based indices, unlike those of dense forests, were not problematic. Thus, the NDVI and TNDVI indices good predictors of the forest parameters in the study area. In addition, the herbaceous layer somewhat reduced the effect of the background soil on recording the actual reflection of vegetation and prevented the soil-based indices from performing better than other classes of indices.

Hudak et al. (2005) showed that linear models had a better fit on stand density than on the stand basal area. In our study, however, similar results were achieved in this regard. This is because the models predicted forest density with an average R2of 0.73 while this value was averagely 0.70 for the canopy cover, which was not significantly different. Using the infrared band of Landsat 8 images,Renoud et al. (2015) predicted only 10.7% of the variation in the stand volume of Fagus orientalis forests in the north of Iran. Thus, forest conditions seem to have a significant effect on modeling results. According to Hudak et al.(2005), in dense forests, LIDAR images are more suitable than Landsat data. In addition, the area of the sampling plot, the distribution of the plots throughout the area and the techniques applied to derive vegetation indices can be highly important. As indicated in the present study, preclassification is an effective technique that helps to achieve robust models with high accuracy and precision.

Our results showed that NDVI and TNDVI in simple parsimonious models are the best predictors of forest parameters. Similarly, as indicated by Patel and Majumdar(2010), only the NDVI index yielded a regression coefficient value of above 0.80 and was sufficient for predicting the biomass of Shorea robusta forests in India. Inversely,Chen and Zhao (2007) showed that, in northeastern Florida,less than 50% of the variance of forest parameters could be explained by NDVI as a predictor. They suggested that more predictors should be included in the models. However, in our study area, the presence of an herbaceous layer on the soil layer (which reduces the background reflectance) or the presence of dark soil may have caused the soil-line-based indices to be no better predictors of forest parameters than the independent ones. In fact, the soil background can be handled well using band ratios, especially for NDVI and TNDVI indices. Moreover, some soil line-based indices such as SAVI have some limitations, and there are potential errors in vegetation estimations, especially in the case of low and high vegetation covers.

The nonlinear models in this study were not superior to the linear ones, except for the cubic and quadratic models for some indices. A cubic model with a higher R2and a lower NRMSE was preferable for NDVI, SRVI and SAVI2. The nonlinear response of NDVI was first demonstrated by Qi et al. (1994). The quadratic model had a better fit on the IPVI data and was preferable to the linear model. Of course, nonlinear relationships require more adjusted parameters (Maire et al. 2012). The data gaps between the classes used in this study (see Fig. 3) may have affected the results obtained for the nonlinear models.These gaps can only be filled by increasing the number of classes and getting a larger number of samples, which is costly. However, it seems logical to think that, in most cases, simple linear models with higher parsimony are suitable for predicting forest parameters in the western forests of Iran.followed by SRVI could be evaluated precisely. Statistical modeling may be the most cost-effective and feasible solution for obtaining density and canopy cover estimates of the western mountain forests of Iran, especially if highresolution images can be used. In this study, we tried to obtain a geographically representative data set by accurately measuring the density and the canopy cover of the forests in the study area. Of course, to gain a better picture of the conditions of the area, more data are warranted, and more tests should be conducted as done in this study. In the non-commercial forests of western Iran, linear regression is the most feasible solution to estimating density and canopy cover in future. Moreover, because of the improved availability and the reduced cost of materials, Landsat-8 imagery data can still be used for the western forests of Iran to predict their density and canopy cover. Finally, to expand the models on a national scale, more reliable data must be obtained by ground measurements.

Conclusions

In this study, vegetation indices derived from Landsat-8 images proved to be suitable for predicting the density,canopy cover, and basal area of the deciduous oak forests in the western mountains of Iran. According to the results of this study, the simple regression technique is well suited for modeling density and canopy cover based on Landsat imagery data. The models tested in this study produced satisfactory results. As the normalized root mean square error was about 10%, the models based on NDVI, TNDVI