万有引力定律的分析与应用

考情分析：万有引力定律的相关内容在近几年的高考中几乎都有涉及,且多数出现在与人造卫星及航天知识相联系的综合题目里。预测在今后的高考中,万有定律与牛顿第二定律、圆周运动等综合在一起出题的概率还会增加,且与实际问题、现代科技相联系的内容也会有所增多。

一、应用万有引力定律的两种特殊思维方法

1.补偿法(运用“补偿法”解题的关键是紧扣规律适用的条件,先填补后运算)。

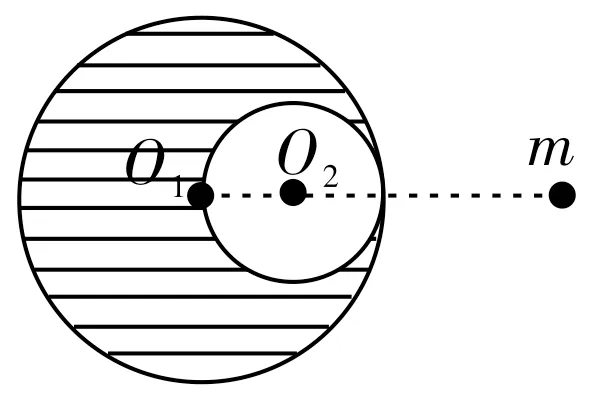
图1

例1如图1 所示,一质量为M的球形物体,密度均匀,半径为R,在距球心为2R处有一质量为m的质点,若将球体挖去一个半径为的小球(两球心和质点在同一直线上,且挖去的小球的球心O2在原来球心O1和质点连线的中间,两球表面相切),求剩余部分对质点的万有引力的大小。

解析：万有引力定律公式适用于求两质点间的万有引力,为满足万有引力定律的适用条件,可应用“等效填补法”,先将被挖去的部分补上。小球未被挖去时,大球对质点的万有引力,由体积公式可知,被挖去的小球的质量M'=,它在被挖去前对质点的万有引力F2=。因此小球被挖去后剩余部分对质点的万有引力

2.比例法(可利用万有引力定律直接求比值,也可以先先求出某一物理量的比值,再利用万有引力相关公式求其他物理量的比值)。

例2火星的半径为地球半径的一半,火星质量约为地球质量的,那么地球表面质量为50kg的人受到地球的万有引力约为火星表面同质量物体受到火星万有引力的多少倍?

解析：设火星质量为M1,地球质量为M2,火星半径为R1,地球半径为R2,由万有引力定律可知

二、常见的三种估算题型

1.根据已知量估算“中心天体质量”。

此类题型的已知量一般为围绕中心天体运动的星体的公转周期、轨迹半径等,根据这些已知量一般可估算出中心天体的质量,比如已知月地距离和月亮绕地球的公转周期,可估算出地球的质量;已知日地距离和地球绕太阳的公转周期,可估算出太阳的质量。需要注意的是求出的是中心天体的质量,而不是绕其运动的星体的质量。

例3我们把地球绕太阳的公转看成是匀速圆周运动,运行轨道平均半径为1.5×108km,已知引力常量G= 6.67 ×10-11N·m2/kg2,则可估算出太阳的质量大约是多少? (结果取一位有效数字)

解析：地球绕太阳的公转周期为365天,即T=365×24×3600s=3.154×107s,万有引力提供地球绕太阳做匀速圆周运动所需的向心力,则1030kg。

2.根据“黄金代换式”计算。

一般情况下,星球表面物体的重力近似等于星球对物体的万有引力,则mg=习惯上,我们称公式GM=gR2为“黄金代换式”。

(1)若题目中已知g、R,即相当于知道了GM,则根据星体运动规律可求解其他物理量。

例4已知地球表面重力加速度为g,地球半径为R,求地球同步卫星离地面的高度h。

解析：地面上质量为m的物体其重力等于地球对它的万有引力,则。地球同