面向广义动态加工空间的机床切削稳定性研究
2020-05-21邓聪颖冯义赵洋魏博
邓聪颖 冯义 赵洋 魏博


摘要 为了研究加工过程中变化的刀尖频响函数导致机床切削参数选择的不确定性,以主轴转速与运动部件位置为研究对象,提出基于广义动态空间的机床切削稳定性研究方法。该方法结合切削颤振理论与切削试验,推导工况下刀尖频响函数计算公式,通过引入正交试验法规划切削试验方案,确定主轴转速与运动部件位置对切削稳定性的影响程度以及最优参数组合,同时计算刀尖频响函数研究机床处于不同转速及位置的颤振稳定域图预测。将该方法运用于某型立式加工中心,识别主轴转速与主轴箱Z向进给位置显著影响切削稳定性,并确定刀具最优姿态,通过计算刀尖频响函数绘制颤振稳定域图,结合切削试验验证了该方法的有效性,为实际加工合理选择切削参数提供技术支持。
关 键 词 切削稳定性;频率响应函数;稳定域图;正交试验;广义动态空间
中图分类号 TG506 文献标志码 A
Research on machine tool cutting stability in the generalized dynamic space
DENG Congying1, 2, FENG Yi1, ZHAO Yang1, WEI Bo1
(1. School of Advanced Manufacturing Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China; 2.School of Mechanical Engineering, Chongqing University, Chongqing 400030, China)
Abstract A method to study the machine tool cutting stability is proposed in generalized dynamic space, which takes the spindle speed and moving parts positions as the objectives, for the variable in-process tool point frequency response functions (FRFs) cause uncertain choices for the cutting parameters. This method combines chatter theory and cutting experiment to derive the formulas to calculate tool point FRF and introduce orthogonal experiment method to arrange the cutting experiment. Thus, the influencing degree of the variables and their optimal combination are determined. Also these tool point FRFs are recalculated to study the cutting stability chart prediction. Applying this method in a vertical machining center, the spindle speed and Z direction displacement were identified to affect the cutting stability mostly, and the best working state for tool was determined. The stability chart was plotted by adopting the recalculated tool point FRF, from which the cutting parameters were chosen to conduct the cutting experiments. The results verify the effectiveness of the proposed method, which lays a technical support for choosing reasonable cutting parameters in machining process.
Key words cutting stability; frequency response function; chatter stability chart; orthogonal experiment; generalized dynamic space
切削加工的不穩定性严重影响机床的加工质量和切削效率,加速机床与刀具的磨损和精度的丧失[1]。机床加工时,由于断续切削、机床自身状况等因素的影响,导致刀具相对工件表面产生周期性的振动,诱发颤振,严重恶化加工零件的尺寸精度和表面质量,使切削难以继续进行[2-5]。切削稳定性与机床动力学特性密切相关,加工过程中刀具位姿使机床整机结构发生改变,进而导致机床振动特性发生演变[6]。同时,与转速相关的主轴系统动力学特性直接影响机床切削稳定性[7-8],因此,研究广义动态加工空间的机床切削稳定性,对于切削现场加工应用,保证零件加工质量,充分发挥机床效率至关重要。
根据上述理论分析,刀尖频响函数辨识可按如下方式进行:
1)确定主轴2个邻近转速,并假设主轴转速的微小变化对刀尖频响函数的影响可忽略,分别在对应的转速下进行切削试验,确定轴向极限切削深度与切削颤振频率的试验值;
2)结合试验值与理论值,根据式(9)建立非线性方程,求解X、Y向主模态对应的[ωi]、[ζi]。
通过理论模型计算与试验相结合的方法,辨识工况下刀尖频响函数,根据式(7)、式(8)绘制切削颤振稳定域图,为研究随主轴转速以及运动部件位置变化的机床切削稳定性奠定基础。
2 基于正交试验设计的广义动态空间切削试验
机床运动部件在加工空间的不同位置组合会改变整机结构的动力学特性,进而影响机床切削稳定性。同时,加工中机床转速,尤其是高转速诱发的离心力效应、陀螺力矩效应以及轴承刚度软化等因素对主轴系统动力学特性有明显影响,直接影响刀尖频响函数,造成机床切削稳定性预测的不确定性。为研究主轴转速、运动部件位置以及它们的不同组合对机床切削稳定性的影响,采用正交试验规划试验方案,可在保证试验质量前提下减少试验次数,提高试验效率[14]。
2.1 正交试验设计基本步骤
正交试验设计主要由试验方案设计及试验结果分析组成,本文采用如图2所示的设计流程。
图2中试验考核指标为轴向极限切削深度[aplim];因素指主轴转速、各运动部件的空间位移;水平指因素的不同取值;表头设计时,本文不考虑因素间的交互作用,各因素可随意安排。
试验结果分析包括极差分析和方差分析。
1)极差分析,通过正交表中任一列的极差R值来确定各试验因素的最优水平与最优组合:
[Ri=maxpi1,…,pij-minpi1,…,pij] , (10)
式中,[pij(j=1,2,…,n;i=1,2,…,n)]为正交表中第i列因素取水平j时所得试验结果的算术平均值。
2)方差分析,基于F检验确定各试验因素对试验指标的影响程度。
[Vi=SifiSi=q=1mkiq-x 2fi=m-1 , Ve=SefeSe=q=1mkep-x 2 , fe=fT-i=1lfi fT=n-1 ,Fi=ViVe , ] (11)
式中:[Vi]表示因素平均方差平方和;[Si]表示正交表中第i列的偏差平方和;[kiq]表示第i列q水平的试验结果均值;m为试验因素的水平个数;[fi]为因素自由度;[Ve]表示误差平均偏差平方和;[Se]表示误差列偏差水平和;[fe]是误差自由度;l为试验因素个数;[fT]为总自由度;n为试验总次数;通过从F分布表中查出临界[Fα(fi,fe)],对比[Fi]和[Fα]确定显著影响因素。
2.2 广义动态空间正交试验设计的实现
以主轴转速与各运动部件位置为设计变量,结合正交试验设计规划切削试验方案,构建广义动态加工空间研究机床切削稳定性,图3为简单的实现流程图。
试验时采用麦克风拾取加工过程中的声音信号,通过频谱分析以及工件表面加工质量判断切削是否发生颤振[15-16],确定切削颤振频率[ωc],并以某加工位置首次发生颤振时的轴向切削深度作为该转速对应的轴向极限切削深度[aplim]。
广义动态空间正交切削试验实施步骤如下:
1)根据正交表规划的试验方案调整刀具加工位置,针对机床进行锤击试验,获取刀尖X、Y向的频响函数与模态参数,完成一组试验后,根据正交表的试验顺序依次调整刀具位置,重复试验,直至获取正交表中所有加工位置对应的刀尖X、Y向的频响函数与模态参数;
2)在Matlab中绘制静止状态下机床在各加工位置对应的颤振稳定域图[17-19],根据此图确定正交表中各转速对应的轴向极限切削深度,作为后续切削试验的初始轴向切削深度[api];
3)结合正交表规划的试验方案、机床加工关键工序的工艺参数以及初始轴向切削深度[api]进行切削试验,分2种情况讨论试验结果:①如果加工时没有出现颤振,则等间距增加轴向切削深度并保证其余参数不变,重复进行切削试验,直到初次发生切削颤振时,以前一次切削试验对应的轴向切削深度作为轴向极限切削深度[aplim];②如果加工时发生颤振,则等间距递减轴向切削深度并保证其余参数不变,重复进行切削试验,直到第一次出现无颤振切削时,以此次轴向切削深度作为轴向极限切削深度[aplim];
4)完成一组方案对应的切削试验之后,根据正交表步骤1、2试驗结果,重复步骤3,依次完成正交表规划的全部试验方案。
在MALAB中对试验数据进行极差分析与方差分析,确定各变量对机床切削稳定性的影响程度以及刀具最优姿态,同时根据工况下刀尖频响函数计算方法,重组各转速与各加工位置的刀尖频响函数,对比分析采用机床静止与加工状态下刀尖频响函数绘制的切削颤振稳定域图。
3 基于广义动态空间的立式加工中心切削稳定性实例研究
以某型三轴立式加工中心为例,机床采用定柱式结构,重点研究主轴转速与工作台、主轴箱等移动部件对机床切削稳定性的影响程度及其最优组合,图4阐述了基于广义动态空间的立式加工中心切削稳定性研究的具体应用步骤。
3.1 主轴转速、移动部件位置分布
研究的立式加工中心中工作台实现沿X、Y方向的移动,主轴箱实现沿Z方向的移动,各向行程为:X-750 mm、Y-450 mm、Z-450 mm。
主轴转速范围为50 ~10 000 r/min,为研究其对机床切削稳定性的影响,首先根据机床使用条件,选择关键加工工序,确定主轴转速的4个转速:2 500 r/min、4 400 r/min、6 200 r/min、8 700 r/min。
为分析机床在广义加工空间的切削稳定性,首先需要离散化加工空间,形成离散的空间位置点,根据工作台、主轴箱的行程,均匀分布移动部件在X、Y、Z方向的位移。
3.2 基于正交试验设计方法的机床切削试验
根据工况下刀尖频响函数辨识方法,需获取2个邻近转速对应的轴向极限切削深度和切削颤振频率,假设主轴所处加工位置不变,主轴转速间隔100 r/min时对应的刀尖频率响应函数不变,根据主轴转速分布和移动部件位移分布,确定主轴转速的4组水平值,X、Y、Z方向位移的4个水平值,构建如表1所示的正交试验因素水平表。
基于因素与水平个数,选择正交试验表L16(45),只采用前4个因素列,建立如表2所示的正交试验表,共规划16组切削试验。
根据正交表试验号依次进行切削试验,由于刀尖频响函数辨识方法的精确程度与试验获取的切削颤振频率和极限切削深度密切相关,为保证试验数据的准确性,在给定的切削参数下重复进行两次切削试验,以切削颤振频率和轴向极限切削深度的平均值作为最终的试验结果。
根据2.2节广义动态空间正交切削试验实施步骤,试验装置包括LMS数据采集系统、ICP型加速度传感器(其灵敏度为99.8 mV/g)、PCB型力锤(其灵敏度为0.23 mV/N)、麦克风等,试验现场如图5所示,试验过程如下:
1)根据正交表2调整刀具位置,对立式加工中心进行锤击试验,获取16组加工位置对应的X、Y向刀尖频响函数以及模态参数;
2)将机床静止状态下获取的刀尖频响函数以及模态参数带入式(1)~ 式(8)中,在Matlab中绘制该16组加工位置对应的切削颤振稳定域图,并输出后续切削试验的初始轴向切削深度[api];
3)根据试验条件及部分切削参数,结合正交表与初始轴向切削深度[api]进行切削试验。以第8组试验为例,图6表示机床以4 400 r/min进行切削加工发生颤振时,麦克风拾取的声音信号对应的频谱,图中主频成分为638 Hz。由于2个相邻主轴转速作为一个试验因素,因此每组切削试验共确定2个切削颤振频率[(ωec1,aec2)]和轴向极限切削深度[(aeplim1,aeplim2)]。
3.3 正交试验结果分析
表2中轴向极限切削深度aplim的实测值在2.19 ~ 4.98 mm之间动态变化,表明加工位置和主轴转速对机床切削稳定性有重要影响。
论文重点探讨轴向极限切削深度[aplim],忽略为辨识刀尖频响函数引入的轴向极限切削深度[aeplim2],仅以轴向极限切削深度[aeplim1]作为考核指标,根据式(10)、式(11)对正交试验结果中的[aeplim1]作极差分析和方差分析,表3与表4分别给出分析结果。
分析表3、表4可知,正交试验最优参数组合为[(n)4][(X)2][(Y)1][(Z)4],表4中主轴转速与主轴箱在Z方向的位置的偏差平方和分别为2.259、0.233,远远大于主轴箱在X方向与Y方向位置时的偏差平方和0.073、0.082。因此,主轴转速对机床切削稳定性的影响最为显著,其次为主轴箱在Z方向的位置变化。实际加工时主轴转速的选取需要综合各方面因素,比确定刀具的加工位置更为复杂,因此可先确定各运动部件所处位置的最优组合,使刀具处于最优姿态,明确主轴转速后,根据论文1.2节提出的方法计算该转速下刀尖的频响函数[20-21],绘制修正后的稳定域图,合理选取轴向切削深度ap。
4 面向加工过程的频率响应函数实例计算
论文以正交表中第8组试验方案为实例阐述加工过程中刀尖频响函数计算方法[22-23],探讨基于广义动态空间研究机床切削稳定性的必要性。
针对第8组方案,试验获取的X、Y向刀尖频响函数曲线与模态参数如图7和表5所示。
表2中每组方案的切削颤振频率ωc预测值集中在600 ~ 690 Hz,因此针对第8组方案,主导机床切削颤振的主模态为表5中各向第2阶模态。加工时重点考虑X、Y方向第2阶模态参数的改变,以各主模态对应的固有频率和阻尼比作为未知量,其余模态参数保持不变。
根据式(7)、式(9),结合第8组方案实测的轴向极限切削深度[(aplim1,aplim2)]和颤振频率[(ωc1,ωc2)],建立4个非线性方程,求解的[ωxi]、[ζxi]、[ωyi]、[ζyi]为:677 Hz、642 Hz、1.63%、3.21%。
通过获取的主模态固有频率和阻尼比重组当前转速下刀尖频响函数,图7中虚线为频响函数曲线计算值。分别对比X、Y向的频响函数曲线,实测值与计算值出现明显的差异,主要是主轴系统在转速场中受离心力和陀螺力矩的影响,主轴轴承运行刚度减小,同时主轴-刀具系统接触面间的接触刚度和接触阻尼也发生变化。
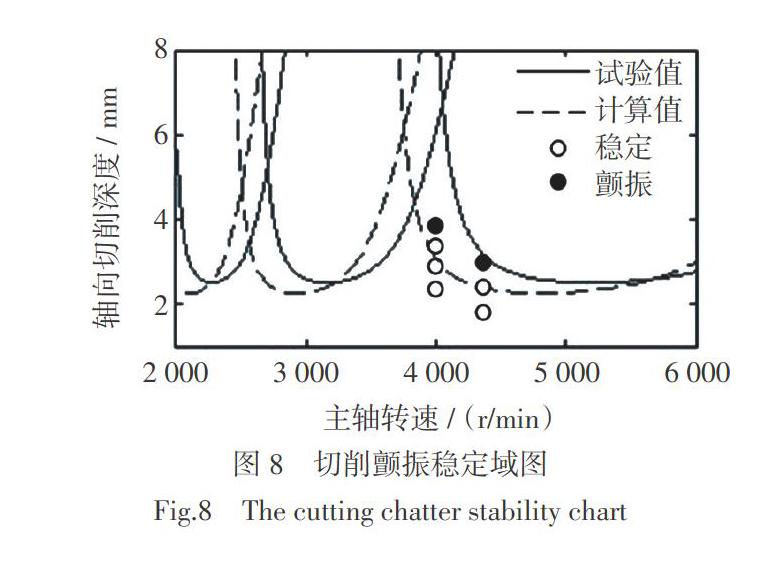
采用频响函数的试验值与计算值在Matlab中绘制图8所示的第8组方案的颤振稳定域图。针对图8建立的穩定区和颤振区进行切削试验,在第8组方案的特定转速4 400 r/min及附近转速4 000 r/min下,切削稳定和颤振的试验结果分布表明采用计算的频响函数绘制的稳定域图预测精度更高,同时采用某特定转速的频响函数绘制的稳定域图也可用于其附近转速的稳定性预测。
5 结论
本文面向加工过程提出基于广义动态空间的机床切削稳定性研究方法,分析主轴转速与运动部件位置的不同组合对轴向切削深度的影响,克服传统切削稳定性分析仅适用于静态场合和固定加工位姿的不足。通过结合某型立式加工中心具体阐述了该方法的应用,辨识出机床主轴转速和Z向位移变化对机床切削稳定性的影响最为显著,通过计算一组工况下的刀尖点频响函数并绘制对应的切削颤振稳定域图,基于切削试验验证了该研究方法的有效性。
