基于改进ORB算法的VSLAM特征匹配算法研究
2020-05-21杨立闯马杰马鹏飞王旭娇王楠楠
杨立闯 马杰 马鹏飞 王旭娇 王楠楠


摘要 针对传统特征匹配算法耗时较长、匹配率不高的问题,提出一种改进ORB的图像特征匹配算法。首先对FAST特征检测算法进行改进,构建非线性尺度空间,采用非线性扩散滤波方法,对金字塔进行构建,通过快速显示扩散形式(FED)进行求解,得到尺度空间上的图像,并采用灰度质心法方法,对特征的角点方向进行计算。然后对FREAK算法采样模式进行优化,采用改进的描述子构建特征向量。最后采用GMS匹配算法剔除伪匹配点对,有效降低误匹配概率。实验证明,相比SIFT、SURF、FREAK、BRISK和ORB算法,本文改进的算法在耗时和匹配率方面均有明显效果,并在旋转、尺度、光照等变换条件下,具有较强的鲁棒性,适用于VSLAM系统。
关 键 词 特征匹配;改进ORB;FAST;特征检测;VSLAM
中图分类号 TP391.41 文献标志码 A
Research on VSLAM feature matching algorithm based on improved ORB algorithm
YANG Lichuang, MA Jie, MA Pengfei, WANG Xujiao, WANG Nannan
(School of Electronics and Information Engineering, Hebei University of Technology, Tianjin 300401,China)
Abstract Aiming at the problem of long time consuming and low matching rate of traditional feature matching algorithm, an improved image feature matching algorithm based on ORB is proposed. Firstly, the FAST feature detection algorithm is improved to build a nonlinear scale space, and the pyramid is constructed by using the nonlinear diffusion filtering method. The image in the scale space is obtained by solving the FAST display diffusion form (FED), and the corner direction of the feature is calculated by using the grayscale centroid method. Then, the sampling mode of the FREAK algorithm is optimized and the improved descriptor is used to construct the feature vector. Finally, the GMS matching algorithm is used to eliminate the false matching point pairs and effectively reduce the false matching probability. Compared with SIFT, SURF,FREAK,BRISK and ORB algorithms, the improved algorithm in this paper has obvious effects in terms of time consumption and matching rate, and has strong robustness under rotation, scale and illumination conditions, which is suitable for VSLAM systems.
Key words feature matching; improved ORB; FAST; feature detection; VSLAM
0 引言
同時定位与地图构建(Simultaneous Localization and Mapping,SLAM)通过搭载某种设定的传感器,在没有环境先验信息的情况下,在运动过程中构建环境的模型,同时估计自己的运动[1]。若此传感器为视觉相机,则称为视觉SLAM,简称VSLAM。经典视觉SLAM框架主要包括视觉里程计(VO)、后端优化、回环检测以及地图构建等部分。精确的图像匹配是系统良好运动估计以及建图过程的前提,因此对特征匹配算法的研究至关重要。局部特征图像特征匹配方法对旋转、尺度变换、光照以及高斯噪声等具有较好的不变性,在智能识别领域,图像已经成为信息获取的重要途径,因而匹配算法在目标追踪[2]、医疗疾病检测[3]、安防监控[4]、工业产品检测[5]、空间遥感技术[6]等重要领域的研究及应用越来越广泛。
作为图像处理学科研究热点,多年以来,国内外学者一直致力于图像特征匹配算法研究。Lowe等[7]在2004年提出著名的SIFT算法,该算法对旋转、尺度、光照等外界条件有较强的适应性,匹配效率较高,但计算复杂度偏高,耗时严重,实时性较差。Bay等[8]在SIFT算法研究基础之上,在2006年提出了SURF算法,采用积分图像与多尺度箱体滤波器进行卷积,运算速度明显提升,但稳定性以及实时性不高。
近年来,一些新的局部特征匹配算法不断涌现。BRISK算法由Leutenegger等[9]在2011年提出,该算法尺度与旋转不变性较好,匹配效率高,对具有高度模糊图像匹配效果最佳。Rublee等[10]在2011年提出ORB算法,该算法通过FAST 检测子[11]和BRIEF描述子[12]组合进行实现,具有高效运算速度,分别比SIFT与SURF算法快2个和1个数量级,但对图像尺度变化适应性差。Alahi等在2012年提出了FREAK算法[13],该算法根据人眼识别物体的原理进行特征采样,匹配速率较快,但对尺度变化图像配准的效果差。因而,本文基于传统ORB算法提出了一种改进的视觉图像特征匹配算法,并通过与SIFT、SURF、FREAK、BRISK和ORB算法的对比实验进行算法可行性分析。
1 改进的VSLAM特征匹配算法
1.1 FAST特征提取算法
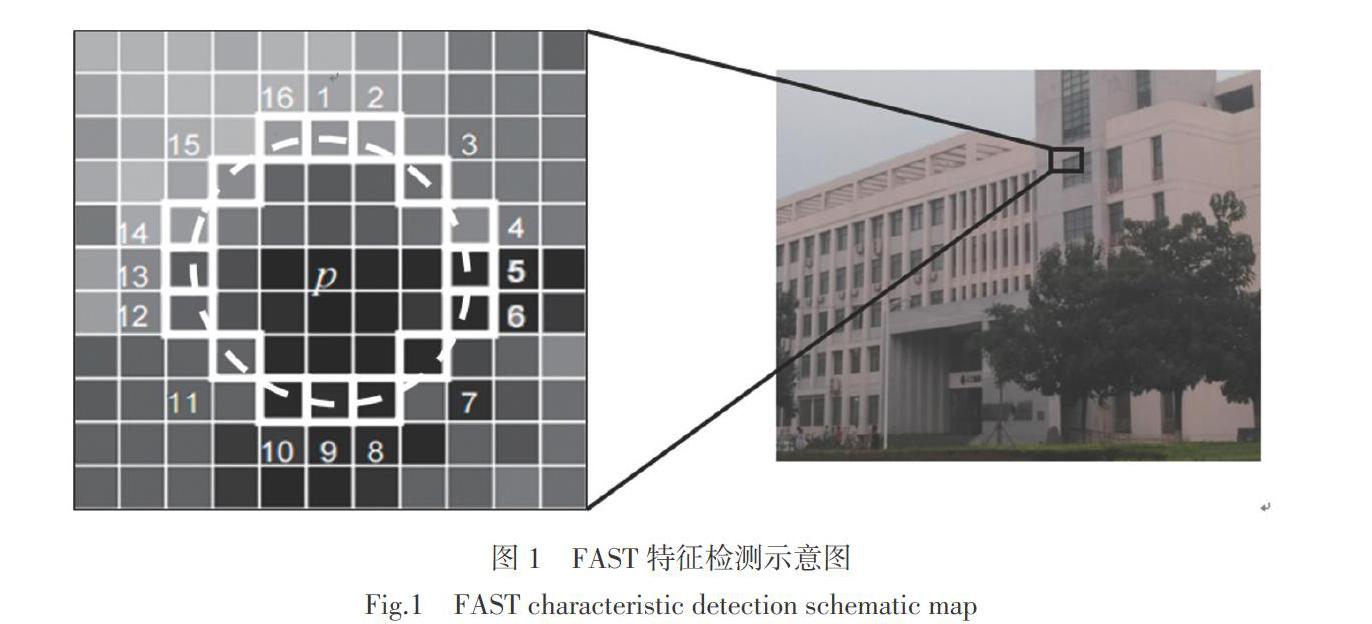
FAST角点算法根据灰度差异程度来检测,计算的时间复杂度较小,检测效果比较突出。FAST角点检测算法角点的定义为:如果图像中某个像素点的灰度与周围邻域内数量足够多的像素点差别足够大,则将该特征像素点认定为候选特征点。FAST特征点检测如图1所示。
在FAST角点检测过程中,检测圆心是像素点p,半径为3像素的离散圆边界上的16 个像素点,若在圆周上存在N个连续像素点,则中心点p是特征点的判断模型[fdet]为
[ fdet=1,|Ix-Ip|>ξ 0, Ix-Ip<ξ ], (1)
式中:[I]表达的是灰度;x表示圆上的点;ξ是设计的一个阈值。
[N=x∈circlepfdet(Ix , Ip)], (2)
式中:N表示全部判断模型的相加总和,参数N为中心像素点p和围绕其的圆环上像素的强度阈值;N的值通常取12,即FAST-12算法。N也经常取值9以及11,即FAST-9和FAST-11算法。当N=12情况时,FAST 特征检测算法获得的特征点效果最好,质量最佳。
1.2 改进FAST特征提取算法
在本文改进FAST特征提取算法中,开始对图像空间加入尺度信息,根据滤波的形式,通过快速显示扩散形式(FED)进行计算,得到尺度空间上的图像。然后采用灰度质心法方法,对特征的角点方向进行计算。
非线性扩散滤波主要目的是对相异尺度空间中图像亮度进行表示,偏微分方程的非线性形式能够对函数散度做描述,具体形式为
[?L?t=div(cx,y,t· L)], (3)
[cx,y,t=g(| Lσx,y,t|)], (4)
[g=11+| Lσ|2/λ2], (5)
式中:[div]为散度;[▽]为梯度;L为亮度;[cx,y,t]为扩散函数;t为表示尺度的参数,与尺度成正比关系;g为区域保留优先级函数; [Lσ]表达高斯平滑,参数是图像标准差σ;λ为对比度因子,与图像边缘信息成反比。
本文通过快速显示扩散方式(FED)对非线性扩散滤波进行计算。循环次数M后,获得图像滤波后总和。其中M = O·S, O和S分别是金字塔的组数和层数。N回迭代表示一回循环,[τj]表示迭代第j回的步长:
[τj=τmax2cos2(π2j+14n+2)], (6)
式中[τmax]是保持迭代稳定的步长最大值。此时显示形式的偏微分方程为
[Li+1-Liτ=A(Li)Li], (7)
式中:[τ]表示某个常量步长;[A(Li)]是传导矩阵。
尺度参数[σi]表示高斯滤波后的滤波参数,其数学形式为
[σio,s=2o+sS], (8)
式中:o∈[0,O-1],s∈[0,S-1],i ∈[0,M]。[σi]表示的是尺度,现在应该把其等效成时间,高斯尺度空间中,图像使用高斯核是标准差σ的卷积和t=[σ2i/2]连续滤波效果相当,所以,尺度参数[σi]与时间[ti]的转换为
[ti=12σ2i]。 (9)
经过[oi]层高斯滤波后,继续对下一层做降采样,使用FED算法,并对λ做调整,从而可获得M次循环共O组S层金字塔非线性尺度空间。
然后采用灰度質心法,对特征的角点方向进行计算。灰度质心法假定某一特征点的灰度与该邻域重心之间存在某种偏移,确定特征点局部区域中的灰度中心C,从特征点P到灰度中心C的方向矢量即为特征点的主方向,定义局部图块区域S的矩为
[Mpq=(x,y)∈SxpyqIx,y, p,q={0,1}], (10)
式中:I(x,y)是像素点(x,y)位置的灰度值。
根据图像块区域中的这些p+q阶矩能够得到灰度中心C的坐标为
[C=Cx ,Cy=M10M00 , M01M00]。 (11)
特征点P与灰度中心C之间的方向角[θ]即为特征点的主方向:
[θ=arctanM01, M10=arctanyIx,yxIx,y, (x,y)∈S]。 (12)
1.3 改进FREAK的特征描述算法
FREAK算法是通过人眼视觉系统启发提出的算法,人眼视网膜根据其感光细胞的密度差异分成4大区域:perifoveal、parafoveal、fovea、foveola,离中心区域越远,神经节细胞密度越小,其结构如图2所示。其中fovea区域负责接收高分辨率图像,而低分辨率图像由最外层区域形成。
FREAK描述子根据人类视网膜感光原理设计,传统的采样模型如图3所示。采用6、6、6、6、6、6、6、1形式的采样结构,除中心特征点外,在7个同心圆上每层采6个样点,一共43 个点数。在上边的样点获取中,中心地方的样点比较多,从中心点向外采样点越来越稀疏。
本文采用简化的5层FREAK描述算子,采样结构为6、6、6、6、1形式,包括25个采样点,如图4所示。采用简化的FREAK描述子对检测到的特征点进行特征描述,这里用F表示构建的二进制位串描述子:
[F=0≤k [T(Pk)=1, (I(Pr1k)-I(Pr2k) >0) 0, 其他 ] , (14) 式中:Pk是当前采样点对;N是生成特征向量的维数;I([Pr1k])是采样点经过高斯平滑的灰度大小。 如果对图像的采样点数为M,则采样点对的对数为[CM2]对。若按照传统FREAK描述子采样模式进行采样,此时采样点总数为43,那么采样点对数为[C432],即有903对采样点。大多数采样点对包含过多冗余或粗糙的信息,对于特征描述意义不大,并且还会增加过多不必要计算。因此采用简化的采样模型构建FREAK描述子,则采样点总数减少为25,采样点对数为[C252],即300对采样点对。为提高描述子辨识度,剔除信息较匮乏的维度,对生成的二进制描述子作维度筛选。 1)构建矩阵D,其任意行皆为简化的FREAK二进制描述子,因此由0和1组成的矩阵D每行包含[C252]个元素,即特征矩阵D的列数是300。 2)计算矩阵D各列均值,越接近0.5的列其方差越大。 3)根据方差递减顺序对各列进行排序,选择前256列为最终特征描述子。 根据视网膜采样模型,分辨率越高维度越低,因此将具有32个字节的FREAK描述子进行分段匹配,首先匹配前16字节,若Hamming 距离小于设定的阈值T,则继续匹配后16字节,否则直接判定为非内点。经过分段匹配策略,可以剔除9成以上的伪匹配。 当描述子分段匹配结束之后,则根据汉明距离进行粗匹配,接着选用GMS匹配算法剔除伪匹配点对,从而有效降低错误匹配点对的出现概率,经过多次相应处理步骤将外点影响降到最低,最终获得满足要求的结果。 2 实验结果与分析 下面利用改进ORB算法、SIFT算法、 SURF算法、ORB算法、FREAK算法以及BRISK算法,对图像的旋转不变性、尺度不变性、光照不变性、模糊不变性以及改进算法的提取的特征点数量和实时性进行分析研究。实验中采用的数据集为用于图像处理特征点识别的标准数据集,即Mikolajczyk和Schmid提供的graffiti图集、boat图集、bike图集和Leuven图集。 2.1 特征点数量及耗时检测 本文通过graffiti图集对图像进行提取特征点时间和数量的测试,在相同的匹配环境下,对相同的一对图像进行比较,测试算法的执行时间以及提取的特征点数。选取graffiti图像组中的第1幅和第3幅图片进行测试实验,改进算法、ORB算法、FREAK算法、BRISK算法、SIFT算法和SURF算法的匹配效果如图5所示,特征点数量和检测时间均值数据如表1所示。 根据表1中可以看出: SIFT算法检测的特征点数量均值最多,但是耗时非常严重,已经高达1 716 ms。SURF算法特征数量检测上效果不错,然而检测时间较长。FREAK算法和BRISK算法在特征数量检测上比ORB算法稍高一些,但耗时分别是ORB算法的1.8倍和2.9倍。本文改进的算法在特征检测上与SURF算法旗鼓相当,耗时仅为10 ms,比ORB算法节省了的8倍时间。相对于SIFT算法、SURF算法、FREAK算法、BRISK算法和ORB算法,本算法在特征点数量以及耗时方面表现出色。 2.2 尺度不变性和旋转不变性检测 本文通过boat图集进行测试。选取boat图像组中的第1幅和第3幅图片,进行尺度不变性以及旋转不变性的对比实验。改进算法、ORB算法、FREAK算法、BRISK算法、SIFT算法和SURF算法的匹配效果和匹配數据如图6和表2所示。根据表2可得:本文改进的算法的匹配率是80%,仅次于SIFT算法,比SURF算法、FREAK算法、BRISK算法和ORB算法的匹配率都高,并且相对于ORB算法匹配率提高了14个百分点。 2.3 模糊不变性检测 通过bike图集进行模糊不变性测试,选取bikes图像组中的第1幅和第3幅图片,进行模糊不变性的对比实验,最终实验的匹配效果如图7所示。本文算法相对于SIFT算法、SURF算法、FREAK算法、BRISK算法和ORB算法的匹配数据如表3所示。根据表3不难看出:本文改进算法的匹配率为92%,与SIFT算法匹配率相当,明显高于SURF算法、FREAK算法、BRISK算法和ORB算法的匹配率。 2.4 光照不变性检测 通过Leuven图集进行光照不变性实验,选取Leuven图像组中的第1幅和第5幅图片,进行光照不变性的对比实验,最终实验的匹配效果如图8所示。本文算法相对于SIFT算法、SURF算法、FREAK算法、BRISK算法和ORB算法的匹配数据如表4所示。根据表4不难看出:本文改进算法的匹配率为88%,仅比SIFT算法匹配率低1个百分点,并且比SURF算法、FREAK算法、BRISK算法以及ORB算法的匹配率要高。 通过上文对改进ORB算法、ORB算法、FREAK算法、BRISK算法、SIFT算法以及SURF算法的实验分析测试,可以看出:本文改进的ORB算法在旋转、尺度、光照等变换条件下,能够出色的实现特征点检测和匹配过程,具有较强的鲁棒性。 3 结论 本文主要对ORB算法进行改进研究,改进了FAST特征提取和FREAK特征描述算法。首先介绍传统FAST特征提取算法,并对特征提取算法进行改进,构建非线性尺度空间,采用非线性扩散滤波方法,对金字塔进行构建,通过快速显示扩散形式(FED)进行计算,得到尺度空间上的图像,然后采用灰度质心法方法,对特征的角点方向进行计算。接着对FREAK的特征描述算法进行优化,改进了FREAK描述子的采样模式,对采样点中的冗余信息进行剔除,提高采样效率和质量。此外采用GMS图像匹配算法剔除伪匹配点对,降低错误匹配点对的出现概率。最后对图像的旋转、尺度、光照和模糊不变性以及改进算法的提取的特征点数量和实时性进行了实验,实验证明本文改进算法在旋转、尺度、光照等变换条件下,能够出色地完成特征点检测和匹配工作,具有较强的鲁棒性,适用于VSLAM系统。 参考文献: [1] 刘浩敏,章国锋,鲍虎军. 基于单目视觉的同时定位与地图构建方法综述[J]. 计算机辅助设计与图形学学报,2016,28(6):855-868. [2] SINHA S N,FRAHM J,POLLEFEYS M,et al. Feature tracking and matching in video using programmable graphics hardware[J]. Machine Vision and Applications,2011,22(1):207-217. [3] GAO L L,PAN H W,HAN J M,et al. Corner detection and matching methods for brain medical image classification[C]//2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM),December 15-18,2016. Shenzhen,China. New York,USA:IEEE,2016:475-478. [4] CHEN P W,GUI C F. Alpha divergences based mass transport models for image matching problems[J]. Inverse Problems and Imaging,2011,5(3):551-590. [5] BLASCHKE T. Object based image analysis for remote sensing[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2010,65(1):2-16. [6] ZHAO M,AN B W,WU Y P,et al. RFVTM:A recovery and filtering vertex trichotomy matching for remote sensing image registration[J]. IEEE Transactions on Geoscience and Remote Sensing,2017,55(1):375-391. [7] LOWE D G. Distinctive image features from scale-invariant key point [J]. International Journal of Computer Vision,2004,60(2):91-110. [8] BAYH,ESSA,TUYTELAARS T,et al. Speeded-up robust features (SURF)[J]. Computer Vision and Image Understanding,2008,110(3):346-359. [9] LEUTENEGGER S,CHLI M,SIEGWART R Y. BRISK:Binary Robust invariant scalable keypoints[C]//2011 International Conference on Computer Vision,November 6-13,2011. Barcelona,Spain. New York,USA:IEEE,2011. [10] RUBLEE E,RABAUD V,KONOLIGE K,et al. ORB:An efficient alternative to SIFT or SURF[C]//2011 International Conference on Computer Vision,November 6-13,2011. Barcelona,Spain. New York,USA:IEEE,2011:2564-2571. [11] ROSTEN E,DRUMMOND T. Machine learning for high-speed corner detection[M]. Computer Vision-ECCV 2006. Berlin,Heidelberg:Springer Berlin Heidelberg,2006:430-443. [12] CALONDER M,LEPETIT V,STRECHA C,et al. BRIEF:binary robust independent elementary features[M]. Computer Vision-ECCV 2010. Berlin,Heidelberg:Springer Berlin Heidelberg,2010:778-792. [13] ALAHI A,ORTIZ R,VANDERGHEYNST P. FREAK:fast retina keypoint[C]//Proceedings of the IEEE Computer Vision Pattern Recognition. [s. n. ]:2012:510-517. [責任编辑 田 丰]
