基于最小二乘蒙特卡洛简化算法的保险公司经济资本度量研究

李秀芳, 杨雅明

基于最小二乘蒙特卡洛简化算法的保险公司经济资本度量研究

李秀芳, 杨雅明

（南开大学 金融学院，天津 300350）

对最小二乘蒙特卡洛方法（LSMC）在保险公司经济资本度量中的简化进行了研究，探讨了该方法在实施过程中的模型处理以及对于嵌套随机模拟的简化效果与效率提升。在此基础上，针对变额年金产品，在不同预测期限下，借助最小二乘蒙特卡洛方法对经济资本进行了度量，并与完整嵌套随机模拟进行了效果比较。研究结果表明，最小二乘蒙特卡洛方法在经济资本度量中起到了良好的简化作用，对于风险损失的尾部拟合具有良好效果。同时相比于经济资本度量中常用的嵌套随机模拟，大大提高了运算效率。

经济资本；最小二乘蒙特卡洛；嵌套随机模拟

0 引言

经济资本是在考虑保险公司自身风险特性的情况下，按照市场一致性价值对保险公司未来面临的非预期损失进行的资本需求度量，是一种基于风险的资本管理手段。近年来，第二代欧洲偿付能力规则（Solvency II）第二支柱中对于公司内部研发基于自身风险的偿付能力评估体系（ORSA）的要求更是促进了经济资本在保险行业中的应用与发展。由中国保监会制定的中国风险导向偿付能力体系于2016年初正式取代了早期以规模为导向的偿付能力测算体系，对整个行业风险管理提出了更高要求。监管法则作为行业总体标准，需要具有简便性、普适性等特征，但对于保险公司内部风险管理而言，基于因子法的监管标准对未来可能的资本市场价值变动刻画能力较弱，对自身风险的特征体现不足。经济资本作为一种基于内部模型的资本管理模式，可以更精确地通过模型化方法实现风险的分解与合并，在资本量化、绩效管理和资源配置等公司运营各个环节上具有较强的适用性。

在经济资本度量过程中，特别是对期限较长的寿险产品而言，为准确度量风险，往往需要对各类风险因子变动及其相互影响进行充分考虑，因此需要进行大量情景生成。正如Bauer等、Reynolds 和 Man等指出，经济资本度量中的情景生成并不刻意的追求某一单个情景估计结果的可靠性，而是通过对各类经济指标进行随机模拟，得到该时刻下经济情景所有可能的情况，从而估计出损失的分布[1,2]。此外，分红、万能及变额年金等寿险产品还通常包含较多的内嵌选择权，对于风险一致性选择权及保证利益的时间价值(TVOG)度量更是需要在大量的风险中性情景模拟的基础上获得，因此合理的嵌套情景生成对于经济资本显得尤为重要。嵌套随机模拟在实际应用中面临的最大障碍就是对于情景生成的可操作性问题，大量的情景生成虽然增加了经济资本损失分布度量的准确性，却对于保险公司经济资本评估的时间和经济成本造成了巨大压力，但过少的情景生成数量则不足以良好模拟未来情景的波动范围和分布状况，因此开发嵌套随机模拟情景的简化算法成为了经济资本度量亟需解决的技术问题。

本文旨在探讨最小二乘蒙特卡洛方法对经济资本度量的简化应用，解决大量情景生成需求下的简化技术问题。文章给出了嵌套随机模拟内外部情景的生成模型，并详细介绍了简化算法操作步骤，最后以一款变额年金产品为例，在多期的角度下对经济资本进行了度量，并在不同置信水平下校验了最小二乘蒙特卡洛方法的测算结果对完整嵌套随机的仿真程度。

1 嵌套随机模拟及其简化算法文献综述

嵌套随机模拟方法在计算市场一致性资产价值与资本需求以及在金融产品定价和风险管理方面具有广泛应用。目前，国内外已有诸多学者对嵌套随机模拟及其简化模型进行了研究。嵌套随机模拟包含外部模拟和内部模拟两个部分，外部情景生成主要用于产生风险因子自当前时点至经济资本度量期末的情景分布，内部情景生成则是以外部情景为基础进一步生成风险中性情景，用以计算内嵌选择权价值。为准确度量经济资本，大量的随机情景模拟是必不可少的，但是实际操作中由于情景数量多、模拟期限长，嵌套随机模拟只能在一定的运算能力约束下进行。Gordy 和Juneja以及Bauer等在总体模拟次数的约束下对内、外部情景数量最优配置进行了研究，并借助Jackknife方法减小模拟偏差[3,4]，邓平紧、李静就内外部情景生成数量对利率风险经济资本结果测算影响进行了分析[5]。Lan, Nelson 和Staum通过对初始外部情景进行筛选,并仅对部分情景进行完整嵌套随机模拟，以获得对损失尾分布较为精确的度量[5,6]。与Lan等通过减少外部情景数量达到控制运算成本的思路不同，Nteukam和 Planchet等的方法研究则注重于内部情景数量上的控制[8]。上述文献中的简化思路是通过寻求有效且少量的内外部情景来替代大量的完整嵌套随机模拟，但在应用中对于尾部风险描述的准确性有待商榷。

此外，另一类简化算法则是通过标准的金融产品对保险资产和负债进行复制，Daul和Vidal以及Oechslin等在这种方法上进行了尝试[9,10]，但由于寿险产品周期较长，基于每一时点的资产匹配技术难度仍然较大，Gan和Lin指出实际中资产组合复制的方法往往难以实现[11]。

基于嵌套随机模拟的简化算法为数众多，为保证对于尾部风险度量的准确性，同时尽量减少路径较长的风险中性情景生成数量，目前经济资本度量简化方法的重点研究方向更集中于对内部情景的简化，其中研究较多的是基于最小二乘蒙特卡洛算法的简化方法。该方法最早由Longstaff和Schwartz提出，核心思路是通过倒推回归的方法进行美式期权定价[12]，之后Clément等和Zanger等人对该方法进行了延伸，并就其收敛性进行了研究[13,14]。杨舸、田澎将人寿保险产品中的退保权视作美式期权，用该方法计算了分红型人寿保险在合同期内各年的退保率[15]。Bauer等首次将最小二乘蒙特卡洛方法应用于保险公司资本需求度量中，并建立了基于保险公司总体资产与负债端的度量框架[4]。此后Bauer等、Teuguia等文章就最小二乘蒙特卡洛简化算法在欧洲“偿二代”下的最低资本测算进行了探讨[1,16]，王灵芝借助该方法对中国第二代偿付能力监管要求中TVOG风险因子进行了校准[17]。

总体而言，最小二乘蒙特卡洛方法对于具有路径依赖特征的金融产品定价具有较强的适用性，因此对含有内嵌选择权的保险业务经济资本度量同样具有借鉴意义。本文提出了实务中基于寿险产品层面的经济资本需求度量框架，并以一款具有退保选择权的变额年金产品为例，分析了最小二乘蒙特卡洛简化算法的实际应用。本文在现有文献研究基础上，通过超均匀抽样提高了代理函数对尾部风险度量的有效性，同时不仅限于通常监管资本要求下的一年期度量期限，而是将经济资本在多年期下，与完整嵌套随机模拟结果进行比较，证实了该方法简化的实用性。

2 基于LSMC的经济资本度量模型

2.1 经济资本与嵌套随机模拟

经济资本是指未来一定期限内，在给定的置信水平下，保险公司为吸收非预期损失而应持有的最低资本，非预期损失来自于资产与负债不利情景的发生，因此经济资本度量的核心在于对损失分布和极端情景的度量。目前，经济资本的情景生成理论与实务比较通行的方法是采用嵌套随机模拟。

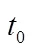
图1 经济资本嵌套随机模拟示意图

Figure 1 Schematic diagram of nested stochastic simulation of economic capital

2.2 正交多项式与最小二乘蒙特卡洛（LSMC）方法

由于异常波动下的风险因子往往是非预期损失发生的主要原因，因此经济资本度量对于风险尾分布的估计水平要求较高，然而外部情景生成对于极端情景生成数量有限，如果完全以外部情景作为最小二乘回归样本，会造成对风险因子极端值的估计偏差，为提高对于风险因子尾部情景拟合的精确性，本文采用Sobol法对外部情景进行抽样以获得风险因子回归多项式。超均匀分布Sobol抽样方法通过在风险因子分布的置信区间内进行规则抽样，避免了样本在均值附近过于集中的缺陷，增加了代理函数对于风险因子极端数值的解释力。关于Sobol抽样方法原理详见Glasserman[18]。

2.3 经济情景生成模型

在对未来经济情景生成过程中，即期收益率采用CIR模型。本文首先通过Svensson法从2008年1月到2017年6月共114期的3个月、6个月、1年、3年、5年和10年期国债收益率数据中获得国债收益率期限结构，拟合并调整零息债券收益率曲线，通过Kalman滤波方法估计国债收益率期限结构用以生成债券内外部情景[19]。CIR模型下现实世界风险测度服从以下过程

3 基于最小二乘蒙特卡洛方法的经济资本度量实施

为完整示例LSMC算法，突出对于具有路径依赖特征的保险产品的经济资本度量过程，本文选取Ledlie等和Cathcart中的GMWB变额年金保单进行经济资本度量[20,21]。

3.1 产品选择及假设制定

最低提取利益保证年金( GMWB)具有如下保单特征。

（1）样本投保人：65岁男性；

（2）账户初始价值：100000元；

（3）保证基准（GB）：初始年度为保费总额，65至75岁期间每年保证账户不低于当年保单账户价值（FV）与上年保证基准（GB）的较大者，同时增幅不超过15%；

（4）每次保证提取的最大金额占保证基准（GB）百分比：5%；

（5）投保人选择权：投保人可以根据市场投资状况选择终止变额年金保证基准给付，并利用账户余额投保其他年金产品；

（6）费用：账户管理与佣金费用率：1.5%，未终止保证基准给付方式前需缴纳保证基准管理费用率：0.75%；

（7）退保率：65至75岁期间退保率为2%，75岁之后，与当前保证提取金额等价的年金产品价格与当前账户价值相比较，随差额增大退保率升高，最低退保率2%，最高为6%，账户价值为0时退保率为0。

3.2 基于最小二乘蒙特卡洛的GMWB产品经济资本度量

图2 嵌套随机模拟账户收益率指数情景示意图

Figure 2 Schematic diagram of nested stochastic simulation account yield index scenario

图3 嵌套随机模拟利率情景示意图

Figure 3 Schematic diagram of nested stochastic simulation interest rate scenario

现考虑用LSMC法对嵌套随机模拟进行简化，首先风险因子的选择是进行最小二乘回归的关键。未来该产品净负债现值主要由保证提取水平、账户价值和折现率共同决定，因此在进行LSMC方法进行回归过程中，本文选取保证基准（GB）、账户价值（FV）和利率（r）作为风险因子。

接下来对每一外部情景通过对偶变量法产生5对内部情景路径，并对各条路径度量未来净负债。同时对于每一外部情景产生的风险因子进行正交化处理，本文所选取的正交基为Legendre正交多项式。

图4 净负债现值与风险因子关系示意图

（保证基准为100000元）

Figure 4 Schematic diagram of the relationship between the present value of net liabilities and risk factors

(guarantee basis: 100000 yuan)

根据(3)式，本文最高选取三次方正交风险因子及其交叉项作为最小二乘回归自变量，进行基于AIC准则的逐步回归，并以此回归关系作为后期内部情景代表，达到简化目的。

图4和图5分别以5年期外部情景为例，描述风险因子与净负债现值关系。如上两图所示，保证基准的提高会使今后年度的提取金额增加，加速账户价值的衰减，从而造成较高负债。当前账户余额价值越高，产生未来负债的时间越晚，因此负债随账户价值的增加而减少，而且当折现率较低时尤为明显。较低的折现率一方面会影响未来给付金额的现值，另一方面还会造成相同支付水平的替代性年金产品相对价值提升，从而增加了GMWB产品的退保率，因此净负债与折现率存在反向关系。表1部分列示了保单年度前二十年的LSMC方法的拟合效果，回归模型结果显示上述三个风险因子对未来净负债变动具有良好的代表作用。

图5 净负债现值与风险因子关系示意图

（保证基准为110000元）

Figure 5 Schematic diagram of the relationship between the present value of net liabilities and risk factors

(guarantee basis: 110000 yuan)

表1 各保单年度LSMC方法拟合优度统计表

3.3 LSMC简化算法结果校验与效率分析

表2 嵌套随机模拟与LSMC简化方法估计误差表（以百分比计）①，其中为真实值，为预测值。

表2中的偏差分析结果显示LSMC算法对嵌套随机模拟的简化效果较好，真实嵌套随机模拟由于会在均值附近产生大量情景，因此当考虑全部情景时会增加评估偏差，而当风险因子在较高的VaR水平下，LSMC方法简化效果非常优良，而极端损失部分正是经济资本的度量核心。

表3 LSMC简化算法与嵌套随机模拟效率比较（单位：秒）

4 结论

本文在市场一致性原则下，对保险公司经济资本度量的简化问题进行了研究，利用最小二乘蒙特卡洛方法对具有内嵌选择权的变额年金产品未来各年度净负债现值拟合结果和运算时间等方面进行了考察，从多期角度对比了最小二乘蒙特卡洛方法对嵌套随机模拟的简化与替代作用，运算结果证实该方法对于尾部风险的刻画效果优良，同时该方法在操作中大大提高了运算效率。在最小二乘蒙特卡洛简化方法中，风险因子及其回归形式是决定预测效果的关键因素，本文使用的超均匀分布Sobol抽样方法保证了风险因子尾分布区域样本的充足性，同时借助正交基底的变换，既可利用风险因子较高次项进行回归、提高拟合精度，又避免了共线性问题，满足了最小二乘回归的模型要求。

在运算机制方面，最小二乘蒙特卡洛方法减少了大量的内部情景生成，而较长的内部情景正是嵌套随机模拟运算较为复杂耗时的部分，因此该方法实现了节约运算时间的目的，使经济资本在保险公司全面风险管理方面具有了更高的实用价值。

[1] Bauer D, Reuss A, Singer D. On the calculation of the solvency capital requirement based on nested simulations[J]. ASTIN Bulletin: The Journal of the IAA, 2012, 42(2): 453-499.

[2] Reynolds C, Man S. Nested Stochastic Pricing: The Time Has Come. Product Matters[J]. Society of Actuaries, 2008, 71: 16-20.

[3] Gordy M B, Juneja S. Nested simulation in portfolio risk measurement[J]. Management Science, 2010, 56(10): 1833-1848.

[4] Bauer D, Bergmann D, Reuss A. Solvency II and nested simulations–a least-squares Monte Carlo approach[C]//Proceedings of the 2010 ICA congress. 2010.

[5] 邓平紧, 李静. “偿二代”框架下情景生成对利率风险经济资本的影响[J]. 保险研究, 2016(9):41-47.

Deng P J, Li J. The Impacts of Scenarios Generation on Interest Risk Economic Capital under C-ROSS[J]. Insurance Studies, 2016(9): 41-47.

[6] Lan H, Nelson B L, Staum J. Two-level simulations for risk management[C]//Proceedings of the 2007 INFORMS Simulation Society Research Workshop. INSEAD, Fontainebleau, France, 2007: 102-107.

[7] Lan H, Nelson B L, Staum J. A confidence interval procedure for expected shortfall risk measurement via two-level simulation[J]. Operations Research, 2010, 58(5): 1481-1490.

[8] Nteukam O, Planchet F. Stochastic evaluation of life insurance contracts: Model point on asset trajectories and measurement of the error related to aggregation[J]. Insurance: Mathematics and Economics, 2012, 51(3): 624-631.

[9] Vidal E G, Daul S. Replication of Insurance Liabilities[J]. 2009.

[10] Oechslin, J., Aubry, O., Aellig, M., Kappeli, A., Bronnimann, D., Tandonnet, A., & Valois, G. (2007). Replicating embedded options in life insurance policies. Life & Pensions, 47-52.

[11] Gan G, Lin X S. Valuation of large variable annuity portfolios under nested simulation: A functional data approach[J]. Insurance: Mathematics and Economics, 2015, 62: 138-150.

[12] Longstaff F A, Schwartz E S. Valuing American options by simulation: a simple least-squares approach[J]. The review of financial studies, 2001, 14(1): 113-147.

[13] Clément E, Lamberton D, Protter P. An analysis of a least squares regression method for American option pricing[J]. Finance and Stochastics, 2002, 6(4): 449-471.

[14] Zanger D Z. Convergence of a Least‐Squares Monte Carlo Algorithm for Bounded Approximating Sets[J]. Applied Mathematical Finance, 2009, 16(2): 123-150.

[15] 杨舸, 田澎. 存在退保时分红寿险定价的最小二乘蒙特卡罗模拟[J]. 管理工程学报, 2006, 20(3):62-66.

Yang G, Tian P.Least Square Monte Carlo Simulation for Valuation of Participating Life Insurance Embedding a Surrender Option[J]. Journal of Industrial Engineering and Engineering Management, 2006, 20(3):62-66.

[16] Teuguia O N, Ren J, Planchet F. Internal model in life insurance: application of least squares monte carlo in risk assessment[J]. 2014.

[17] 王灵芝. 基于一致性原则的偿二代TVOG风险因子校准[J]. 保险研究, 2015(12):30-39.

Wang L Z. The Risk Calibration of TVOG in “C-ROSS” under the Consistency Principle [J]. Insurance Studies, 2015(12):30-39.

[18] Glasserman P. Monte Carlo methods in financial engineering[M]. Springer Science & Business Media, 2013.

[19] Chen R R, Scott L. Multi-factor Cox-Ingersoll-Ross models of the term structure: Estimates and tests from a Kalman filter model[J]. The Journal of Real Estate Finance and Economics, 2003, 27(2): 143-172.

[20] Ledlie M C, Corry D P, Finkelstein G S, et al. Variable annuities[J]. British Actuarial Journal, 2008, 14(2): 327-389.

[21] Cathcart M J. Monte Carlo simulation approaches to the valuation and risk management of unit-linked insurance products with guarantees[D]. Heriot-Watt University, 2012.

The research on the simplified algorithm of economic capital measurement of insurance companies based on least square monte carlo method

LI Xiufang, YANG Yaming

(School of Finance, Nankai University, Tianjin 300350, China)

With the introduction of the Chinese Risk-Oriented Solvency System (C-ROSS), management for insurance solvency capital focuses more on the actual risk exposure rather than before. An insurer can project the value of their assets and liabilities to some future time using Monte Carlo simulation to reserve adequate capital to cover the risk with a high level of confidence. However, the huge amount of computation seriously hinders its application in practice. This paper applies the LSMC method as a simplified algorithm to measure Economic Capital as well as discusses the practical application and simplification effects of this method. Taking a GMDB product with an embedded option as an example, this paper tests the fitting effect of the simplified algorithm with crude nested stochastic simulation. The results show that the LSMC method could make a good performance in the simplification, especially for the tail distribution for risk.The main content includes the following:

Firstly, based on the computational inefficiency of nested-simulation and the path-dependent character of many insurance investment accounts, this paper builds up a regulation based approximation model known as Least Square Monte Carlo (LSMC). This method can efficiently simplify the inner simulation that occupies most of the computational resources of nested-simulation. With the use of LSMC, a large amount of risk-neutral scenarios can be represented by the combination of the finite orthogonal base. As such, the scenario generation for several risk factors in the proxy function is sufficed.

Secondly, this paper adopts low-discrepancy sampling, risk-neutral calibration, and stepwise regression techniques. Sobol sampling at the end of each outer scenario could effectively avoid the excessive concentration around the mean value, which could guarantee the sample adequacy of the tail risk. And then, at the stage of inner scenario generation, the risk-neutral calibration eliminates the effect of risk premium in the parameters estimated by the historical data. At last, the stepwise regression withLegendre polynomials makes sure the proxy function completely unaffected by the multicollinearity of risk factors.

At last, we use a Guaranteed Minimum Death Benefits (GMDB) insurance product with embedded options and Chinese economic data as an example to testify the simplification effect of the LSMC method. It shows that the LSMC model can well match the crude nested-stochastic simulation, especially for tail loss, which is the critical focus of both insurance companies and regulators. It also dramatically shortens the running time. The use of the LSMC method for Economic Capital improves the level of insurance companies’ risk management with practical significance.

Economic capital; Least square monte carlo; Nested stochastic simulation

2017-01-10

2018-05-03

F840.32

A

1004-6062(2020)03-0169-006

10.13587/j.cnki.jieem.2020.03.018

2017-01-10

2018-05-03

国家自然科学基金资助项目(71573143)

李秀芳（1966—），女，天津人；南开大学金融学院、中国特色社会主义经济建设协同创新中心，教授，博士生导师；研究方向：风险管理，精算学。

Funded Project: Supported by the National Natural Science Foundation of China (71573143)

中文编辑：杜 健；英文编辑：Charlie C. Chen