压电液压快速工具伺服系统控制方法的研究

刘晓飞，张 堃，宋国翠

(中山火炬职业技术学院，广东 中山 528437)

0 引 言

快速工具伺服系统(FTS)被广泛研究并应用于工业制造、航空航天、国防军事、天文观测等多个领域，FTS具有高频响、高精度的特点。目前面临一大技术难题是设计有效的控制器。在这方面国外学者做了研究大量研究，也取得不少成果[1]。 Fu J T等人采用PID控制方法效果良好，但是对模型参数要求高，影响系统的稳定性，并且频率不高[2]; 刘春芳等人使用了免疫重复控制的策略，取得了较高控制精度，但存不能准确跟踪给定信号的缺陷[3]；黄庆等人则采用模糊自抗扰技术，取得良好效果，但方法过于复杂，实际操作比较困难[4]。

笔者采用一种压电液压快速工具伺服系统，可充分发挥其响应快、精度高的特点，以具有积分作用的线性二次高斯控制器(LQGi)作为内环控制器。采用高增益反馈(重复控制)相结合的方法来跟踪谐波分量和前馈迭代学习控制(ILC)相结合的方法来实现对重复非谐波分量的跟踪。通过仿真验证了本方案的可行性与有效性。

1 实验装置

采用一种新型压电液压快速工具伺服系统，基于60 μm行程PZT的新型FTS设计，与设计行程和带宽分别为1 mm和400 Hz的液压放大方案耦合。这种设计的优点是轴向放大，降低了对阿贝误差的敏感性，具有紧凑的放大器设计和高带宽行程比。

实验装置由FTS装置本身及其相关放大器、压力和位移传感器的外部信号调节器、实时目标和主机等部件组成。实时目标是安装了PXI-7833R多功能RIO数据采集卡的仪器PXI机箱。该系统在所有实验中均以10 kHz采样，实验设置系统图见图1所示。

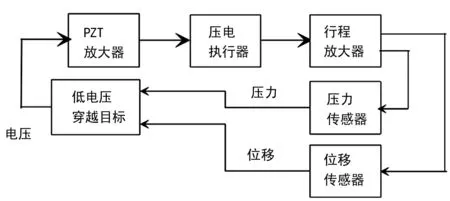
图1 实验设置系统图

对于高性能控制设计，黑盒系统辨识模型更适合。使用动态信号分析仪在5 Hz～5 kHz的频率范围内进行开环装置的四次扫描正弦识别(控制电压至尖端位移)。输入幅度从1 V变化到5 V。结果发现系统具有非线性;最低振幅扫描与较高振幅扫描具有根本不同的波德图。为了研究这种非线性的来源，进行了静态实验，其中将直流步进给到PZT放大器，并且用外部传感器测量实际尖端位移，以消除作为非线性源的传感器。发现存约2 V的死区，之后位移与控制电压成线性关系。虽然存在死区，但它不影响系统传递函数的变化，因为大多数时候控制信号不进入死区。由于放大器设备在PZT上放置了大量负载，因此PZT放大器可能存在电流饱和问题，所以PZT驱动电子设备影响系统传递函数的变化，

为了尝试在装置上使用线性控制，我们假设内环控制器可以将控制电压保持在线性区域。对于出现的强烈的谐波分量，提出了一种高增益反馈(重复控制)相结合的方法来跟踪谐波分量和前馈迭代学习控制(ILC)相结合的方法来实现对重复非谐波分量的跟踪。以具有积分作用的线性二次高斯控制器(LQGi)作为内环控制器。

2 LQGi控制设计

LQGi控制是将系统辨识模型放入状态空间形式，如公式(1)所示。设备型增加了一个额外的状态， 公式(2)所示：

(1)

(2)

LQGi控制器在MISO系统中，其输入是工厂输出y和误差r-y。控制器取得到公式 (3)的形式。

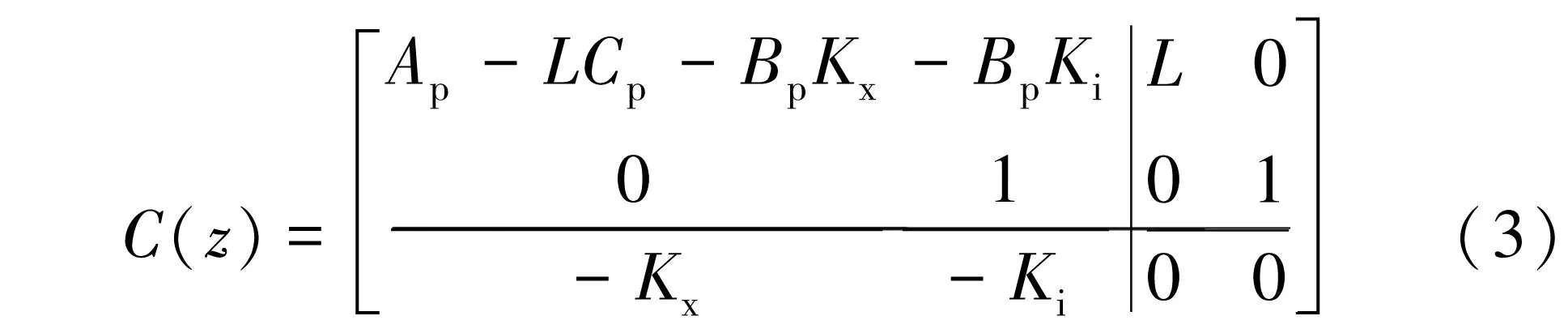
控制器取决于参数kx、ki和L，分别是状态反馈、积分器和观测器增益。通过求解代数黎卡提方程(ARE) ，得到了状态反馈和积分器增益。将离散时间的解决方案称为加权矩阵Q和R为dlqr(A，B，Q，R)。这样得到状态反馈增益如下：

[KxKi]=dlqr(Aaug,Baug,Qk,Rk)

(4)

其中加权矩阵Qk和Rk参数化如方程式(5)所示：

(5)

使得我们可以用两个参数来参数化LQGi控制器：一个控制状态反馈部分，另一个控制积分器。

观测器增益是通过求解ARE, 如公式 (6)，使用加权矩阵Q0和R0作为调整参数。

(6)

3 ILC控制设计

首先，根据方程式(8)和图2中的更新定律，允许ILC收敛到最终的前馈输入序列。图2中Q是一个线性相位低通滤波器环节，如公式(7)所示，阶数为6，用于降低建模不当的高频系统动力学的影响。L是闭环装置G的倒数，可以通过零相位误差跟踪控制(ZPETC)获得。在学习过程中，重复控制器保持断开状态，不允许干扰。这使得ILC和重复控制器可以单独设计。

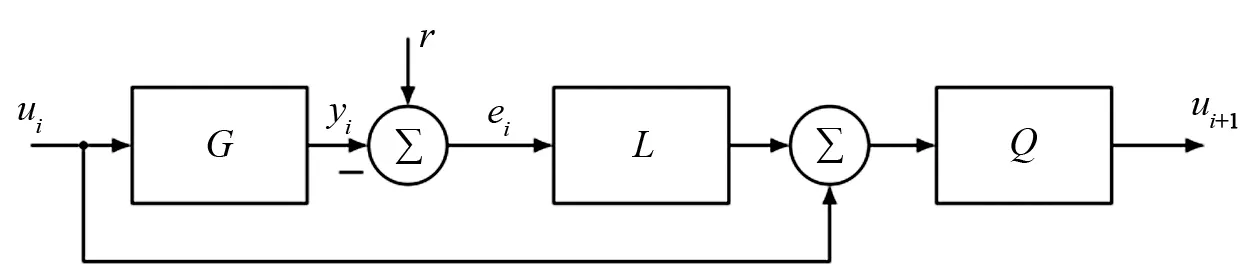
图2 ILC控制器结构

学习过程的迭代性质允许更积极的低通滤波器，通过设置小的学习增益来确保每个连续的迭代与前一次迭代的差别最小。这使得我们能够比重复性的高增益反馈型控制器更深入地探索高频区域。

(7)

uILC(k+1)=Q[uILC(k)+uLe(k)]

(8)

在ILC收敛到稳态前馈输入后，自适应停止，ILC表现为静态前馈滤波器。此时，重复控制器连接并衰减误差中其设计基频的任何剩余谐波。

4 重复控制器设计

完整控制器的框图如图3所示;在该图中，Q再次是零相位低通滤波器环节，如公式(7)所示，但是10阶，并且F与用作ILC公式中的学习滤波器的滤波器相同。

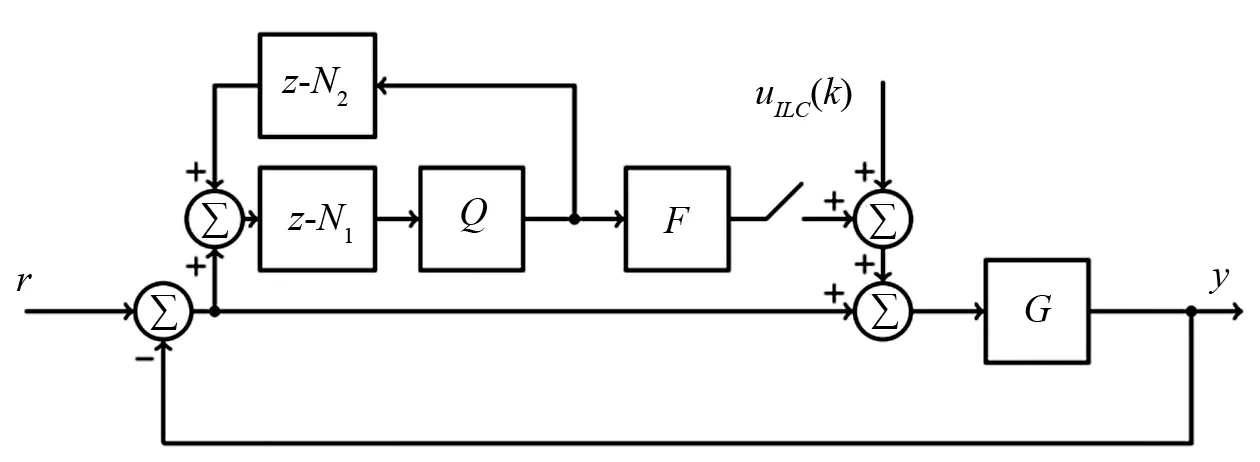
图3 控制器框图

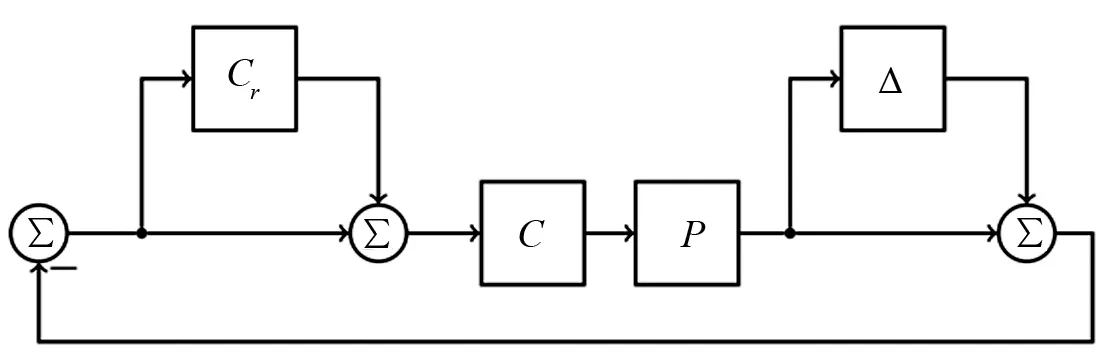
图4 乘法不确定性模型

重复控制设计的主要变量是低通滤波器Q传递函数，其阶数经过优化以保证鲁棒稳定性。对带有重复插件控制器的LQGi闭环进行了鲁棒稳定性和灵敏度分析，如图4所示。通过控制设计模型与原始频率响应数据之间的差异，计算出控制设计模型的不确定性界限。从小增益定理出发，鲁棒稳定的一个充分条件|TWr|<1，其中T是互补灵敏度函数，Wr是先前得到的不确定性界限。为了计算灵敏度和互补灵敏度函数，必须得到回路增益。假定参考值为零时，MISO LQGi控制器可以缩减为SISO控制器C=C2-C1，其中C1是MISO控制器从工厂输出到控制(状态反馈部分)的传递函数，C2是传递函数从误差到控制，通过这种简化，可以显示环路增益：

L=(1+Cr(z))(C2(z)-C1(z))P(z)

(9)

(10)

Cr代表重复控制器，定义如方程式(10)所示。一旦获得环路增益，就可以计算灵敏度和补充灵敏度函数。验证方程式|TWr|<1条件的图形方法是绘制两个函数的幅值，并确保T在整个频带内低于Wr，如方程式(9)所示。对于仅用LQGi控制器的情况，并且插入式重复控制器打开，得到了互补灵敏度函数。为了实现鲁棒稳定性，必须对重复公式中的低通滤波器Q传递函数进行调谐，以切断互补灵敏度函数中由于重复瞄准基本重复频率的所有谐波而产生的高频峰值。由于滤波器Q传递函数的作用，为了实现鲁棒稳定性，灵敏度函数中的正态深重复缺口最大仅下降40 dB。

5 实验结果

第一个实验是只使用内环LQGi控制器跟踪轮廓。从跟踪结果可以清楚地看出，内环控制器虽然能够很好地跟踪大部分谐波段的振幅，但相位延迟较大。这导致其整体跟踪性能最差，均方根误差(RMSE)为53.1 μm。为了减小相位误差，除了LQGi内环外，还开启了重复控制器，重复控制虽然纠正了相位误差，但不能完全跟踪基准，特别是在方向变化附近，而且在斜坡和实际轮廓之间的过渡过程中会出现较大的瞬态。重复控制器比单用LQGi更好，将均方根误差降低到10.4 μm。对于第三个测试，ILC与内部回路LQGI控制器一起启用 ,这产生了迄今为止最好的整体跟踪性能，也补偿了大振幅段中的相位延迟。然而，这些测试是在理想条件下进行的，没有像切割金属那样给刀架施加干扰力。重复控制器的加入增加了抗干扰能力，也提高了性能。组合控制器的结果表明重复控制器的加入使在2.8 μm均方根误差下测试的所有控制器的跟踪性能最佳。跟踪结果汇总在表 1中。从频谱上看，在轮廓的主要谐波分量(100 Hz)处，重复控制单独提供约40 dB的误差减小，ILC单独提供近60 dB，组合控制器将误差信号中的谐波减小70 dB。

表1 控制结果汇总表

对黑盒系统进行了辨识，得到了控制设计模型。研究并表征了系统的非线性，为了减小其影响设计了一种内环路控制器。设计组合反馈和前馈外环控制器，并在物理系统上进行了设计和实现，跟踪了实际测试模式。通过实验验证了组合控制模式在所有控制器排列中的跟踪误差最小。

6 结 语

针对压电液压快速工具伺服系统，提出了以具有积分作用的线性二次高斯控制器(LQGi)作为内环控制器，采用高增益反馈(重复控制)相结合的方法来跟踪谐波分量和前馈迭代学习控制(ILC)相结合的方法来实现对重复非谐波分量的跟踪。仿真结果表明，所提出的控制方法取得了良好的效果，该方法能够对系统进行快速响应，且具有较强的抗干扰性能，改善了系统的稳定性，提高了加工精度，最终验证了本方案的可行性与有效性。