变论域模糊PI控制的SVG系统建模与仿真

王 伟，杜 娟，2，张永丽，王 瑶

（1.北京石油化工学院信息工程系，北京102617；2.北京化工大学信息科学与技术学院，北京100029）

1 引言

随着大量的非线性用电设备涌入电网，其在工作时消耗了大量的无功，造成电网电能的损耗，也影响了电网的供电质量[1]。无功补偿技术是目前普遍采用的提高电网的功率因数，降低电能损耗，提高供电质量的重要措施之一。无功补偿装置的发展经历了从最初的并联电容器和同步调相机到现代的静止无功补偿器（SVC）和静止无功发生器（SVG）。SVG相对于其它补偿装置有调整速度快、适用范围广、谐波小的性能优势，且装置结构紧凑、成本低。SVG从整体结构上来说有三相三线制和三相四线制两种形式，但由于三线制的SVG不能解决现今电网中所存在的冲击性负荷和电网三相不平衡的问题。四线制的SVG能解决这些问题，但是由于其控制技术还不够完善，因此它还没有被大范围的应用。可见，开展SVG控制技术的研究是关键[2]。

三相四线制的SVG又分为三单项全桥结构、三桥臂结构和四桥臂结构。其中，三单项全桥结构控制简单，但它所需要的元器件多、体积大、成本高，所以并不应用中在实际工程中。三桥臂结构主要是根据直流侧两电容中间的中性线来使零序电流分量形成回路[3]。但是其在工作时要求两个电容的电压一致，这在现实应用中很难保证。为实现两电压之间的均压，控制中加入了PI控制[4]。在此研究基础上，又提出了自适应PI双闭环控制方法。与PI控制比，其提高了直流侧电压的稳定性，但是增加了控制的难度[5]。而四桥臂SVG可以用第四个桥臂控制中性点电压，降低了控制难度。

对于四桥臂结构，PI控制的响应速度慢、超调量大、稳态精度不高[6]，因此在PI控制方法的基础上提出了模糊PI复合控制方法[7]。此方法在设计模糊控制器时，大多都是利用经验整定模糊隶属函数的论域，因此对直流侧电压不能做出最好的控制效果。基于此，提出了一种基于变域论的模糊PI控制方法，主要针对SVG直流侧电压的特性，利用误差的变化实时调整模糊控制器论域的范围，抑制因误差变化过大而对系统的干扰，提高系统的稳定性和鲁棒性。

2 SVG主电路拓扑结构及其控制方法

SVG的主电路采用三相四线制四桥臂结构，该结构为电压桥式结构，主电路控制技术采用直接电流控制。其拓扑结构，如图1所示。

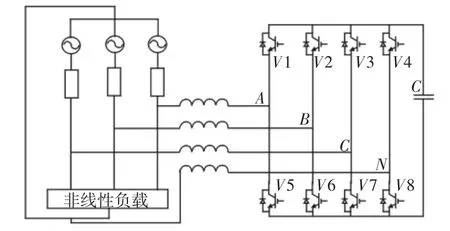
图1 四桥臂的SVG的拓扑结构图Fig.1 Topology Diagram of the SVG of the Four Bridge Arm

3 SVG直流侧电压控制

SVG在实际应用中，若是其直流侧的电压出现剧烈的波动，就会使得整个系统处在欠补或过补的状态中，达不到补偿效果，所以对于其直流侧的电压的稳定性控制是至关重要的。

3.1 SVG直流侧电压的PI控制

目前，大多SVG采用PI控制方法来使其直流侧电压保持稳定。主要是在得到Udc与U*dc的误差之后经PI调节后将输出量id叠加到分离出来的基波正序有功电流的直流分量上，产生与之相对应的指令电流。从而使SVG发出或者是从电网中吸收所需的有功电流来保持直流侧电容电压不变。基本关系，如式（1）所示。

式中：Kp—比例调节系数；Ki—积分调节系数。

3.2 SVG直流侧电压的模糊PI控制

PI控制器不能根据负载的实际情况来调整参数。然而，在电网系统中大量的控制对象是存在着非线性和时变性的，所以PI控制对于直流侧电压的控制效果会受到了限制。基于此，用模糊规则[8-9]对PI控制器的参数进行调整，基本关系，如式（2）所示。

模糊PI的输入采用的是直流侧电压误差E和直流侧电压误差变化率Ec，输出为比例系数自整定量ΔKp和积分自整定量ΔKi。归一化论域均设为［-0.4，+0.4］，根据仿真的动态范围［Emin，Emax］，［Ecmin，Ecmax］，［ΔKmmin，ΔKmmax］，m∈（p，i），可以求得量化因子KE，KEc和比例因子KΔKm，m∈（p，i），如式（3）所示。

采用Mamdani的推理规则，用加权平均清晰化得到输出，经过PI整定后可以得到其参数，如式（4）所示。

但模糊PI控制器在选定了论域和参数之后系统就只能在某一些确定的工作区域进行模糊化和清晰化，当误差（E）和误差的变化率（Ec）过大或过小的时候，系统没办法调节参数使得工作区域变得更具有全局性，而在实际应用中，可能会出现负载变化较大的情况，这就使得模糊控制器不能在任何时候都能获得良好的控制效果。

3.3 SVG直流侧电压的变论域模糊PI控制

基于对以上控制方法的分析比较，提出了一种基于变论域的模糊控制方法，主要是利用了误差（E）和误差的变化率（Ec）的变化调节论域的范围，保证覆盖到所有的论域，提高模糊规则的利用率，并解决了工作区域局限的问题，提高整个系统的精确性。

3.3.1 变论域伸缩因子的调整规则

变论域模糊控制的思想[10]是在模糊规则确定的情况下利用误差信号来改变模糊隶属函数的论域值。模糊论域变化，如图2所示。

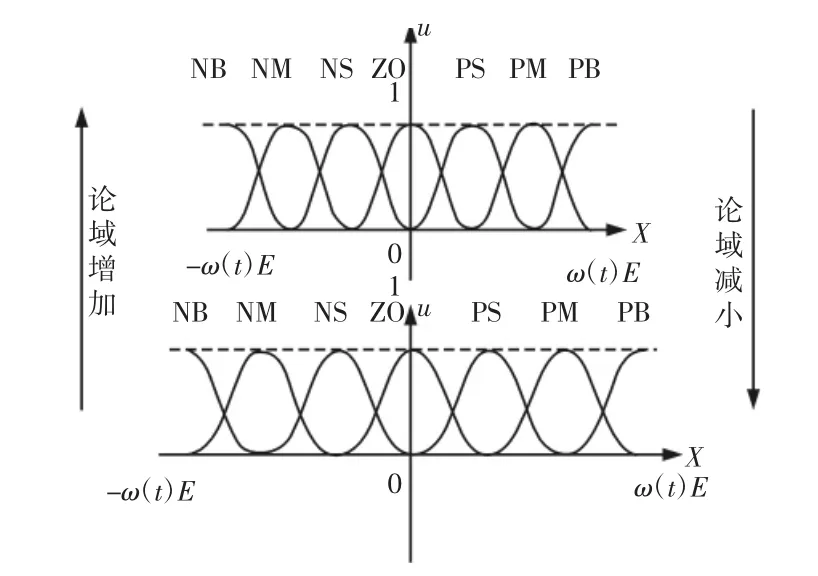
图2 论域变化示意图Fig.2 Sketch Map of Domain Change

图中：NB、NM、NS—负向从大到小；ZO—零；PB、PM、PS—正向从大到小。

设E和Ec作为输入论域的伸缩因子分别是α1和α2；其输出论域的比例因子为Kp，Ki两项，对应两个伸缩因子β1，β2。一般情况下，伸缩因子采用的函数形式，如式（7）～式（9）所示。

式中：KI—比例常数。

为使系统不增加超调，α1和α2在E和Ec增大时应保持不变；当E或Ec减小时，为了使模糊规则能更好的适用于误差的变化，其论域应随之缩小，提高控制精准性，降低模糊规则局限性。输入论域伸缩因子调整规则，如表1所示：

表1 输入论域伸缩因子调整规则Tab.1 The Domain of the Expansion Factor of Input Signal

表中：B、M、S、Z—论域程度由大到小。

输出论域的伸缩因子β的变化应根据E和Ec的变化确定，当E和Ec同时增大或减小时，β的取值应也同向变化，保证系统的灵敏度；而两者非同向变化时，这时系统与目的值之差较大但正在快速收敛，这时候可以不改变控制量，同时β变得较小一些，压缩论域；当E趋于零而Ec变化依然很大时，说明系统已收敛至目的值，但是出现超调，这时增大输出论域以抑制系统偏离的趋势。输出论域伸缩因子调整规则，如表2所示。

表2 输出论域伸缩因子调整规则Tab.2 The Domain of the Expansion Factor of Output Signal

表中：VB，MB，SB，ZO，S，VS—论域程度由大到小。

3.3.2 变论域模糊PI控制器

当伸缩因子接收到E和Ec信号时会进行自调整，并将调整结果与信号一起传递至变论域模糊控制单元，利用事先设定的模糊规则与变化后的论域进行实时调整，得到的参数值传递到PI控制器中，从而对系统进行控制。变论域模糊PI控制器的结构，如图3所示。

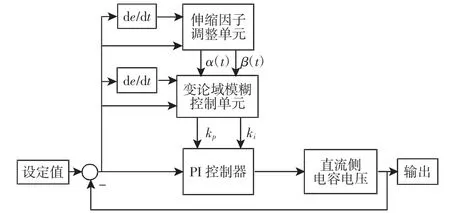
图3 变论域模糊PI控制的示意图Fig.3 A Schematic Diagram of Fuzzy PIControl in a Variable Domain

对于输入论域的伸缩因子计算，如式（10）～式（11）所示。

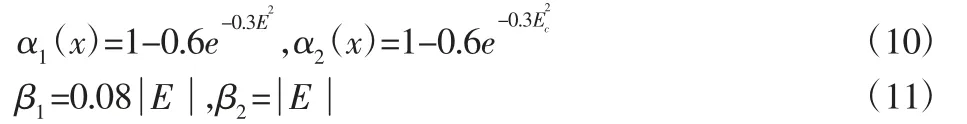
4 建模与仿真

以河北省某鞋厂的电力系统为控制对象验证所提出的变论域控制器的可行性。根据该鞋厂一年的数据分析得到最小功率因数是0.77，期望补偿后的功率因数达到0.95，所需的无功补偿量Qc=140kvar。基于此模拟电网环境以及得出仿真时所用到参数电网电压为380V以及负载值。可以计算出有关SVG参数：直流侧电压Udc=900V，直流侧电容C=4700μF，滤波电抗器L=1.5mH，功率器件IGBT的额定电流ICN=451A，额定电压VCES=1298V。

在传统PI控制、模糊PI控制以及变论域模糊PI控制下直流侧电容电压的对比图，如图4所示。从图中可以看出传统PI控制在系统稳定后的（8～10）s之间还会有震荡，模糊PI控制解决了其震荡问题，稳定性好；变论域模糊PI控制法相对于其他两种方法比较，其超调量更小，收敛速度快，鲁棒性好。可以看出在补偿前其功率因数大概在0.77，在加入补偿装置后其功率因数可以很快达到0.95。在变论域模糊PI控制下的系统补偿前后单相电流的对比图，如图6所示。可以看出补偿前电流有小幅震荡，并不稳定。在加入SVG补偿后系统电流得到了改善。

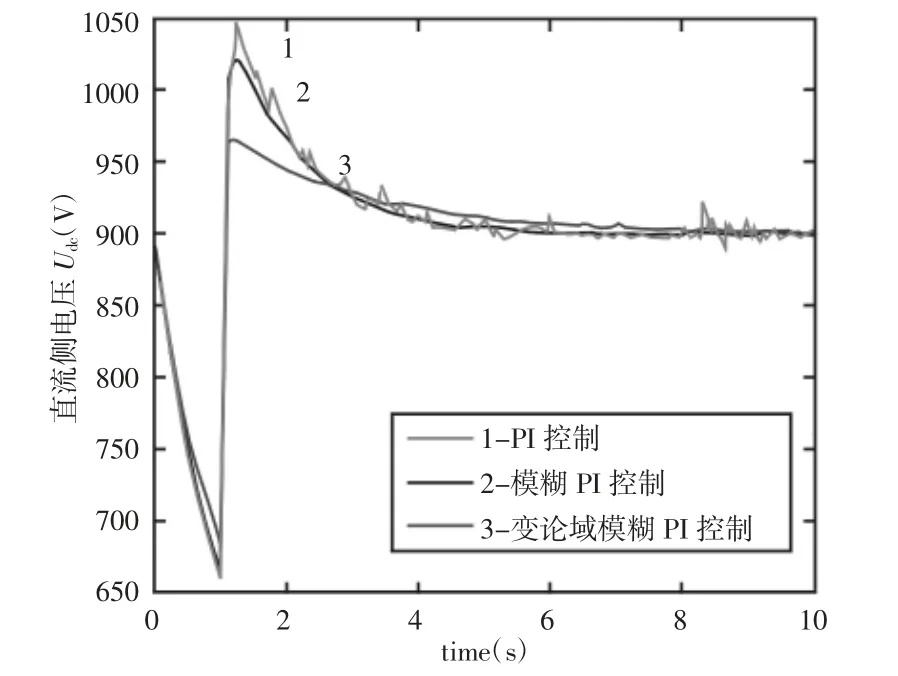
图4 三种PI控制下的对比图Fig.4 Contrast Diagram Under Three Kinds of PIControl

在变论域模糊PI控制下的系统的功率因数，如图5所示。

图5 变论域模糊PI控制下的功率因数图Fig.5 Power Factor Graph Under Variable Domain Fuzzy PIControl

图6 补偿前后单相电流对比图Fig.6 Single Phase Current Contrast Diagram Before and After Compensation

5 结论

针对三相四线制四桥臂结构的静止无功发生器（SVG）直流侧电容电压稳定的控制方法进行了探讨，提出了基于变论域的模糊PI控制法。通过仿真分析可见：传统PI控制和模糊PI控制的超调量分别约为16%和13%，模糊PI控制较传统PI控制的超调量有所改善；基于变论域的模糊PI控制的超调量约为7%，相较于前两种方法其超调量有较大下降，其控制效果要好于前两者。同时，基于变论域的模糊PI控制法的响应速度相较于其它两种控制方法也有约10ms的提升，这对于冲击负荷的补偿具有重要意义。总之，所提出的基于变论域的模糊PI控制法，克服了传统PI控制实时性差、稳定后出现小幅震荡以及模糊PI控制器所出现的收敛速度慢的问题，提高了控制系统的控制精度及鲁棒性。