Mohr-Coulomb准则的试验验证与修正

2020-05-21

中南大学学报（自然科学版） 2020年2期

(中南大学土木工程学院，湖南长沙，410075)

强度理论是研究材料在复杂应力状态下破坏规律的科学[1]，进行工程设计和结构稳定性分析时，正确描述材料的变形破坏规律至关重要。到目前为止，国内外学者已提出许多强度准则，但都有一定适用范围和应用条件。强度准则较著名的有Drucker-Prager[2]准则(D-P准则)、修正的Lade准则[3]、Mogi-Coulomb[4]强度准则(M-C 准则)等。然而，大量的研究表明，没有1个准则相对其他准则而言有明显优势[5-6]，如：D-P 准则假定了材料拉压强度相等，与大多数试验结果不符；修正的Lade准则与Mohr-Coulomb准则预测的三轴拉伸强度不相等。虽然Mogi-Coulomb[4]强度准则对真三轴数据拟合精度有了明显提高，但在偏平面内不满足外凸性条件；SINGH等[7]引入指数函数对高围压状态进行了修正，提出了非线性M-C准则公式，但在应用中发现该准则适用性有限，因此，有必要进一步对强度准则进行研究。M-C 准则概念简洁明了，参数少且易于通过试验获得，广泛应用于岩土工程中[8-11]，为此，本文作者针对M-C准则进行进一步试验验证与修正。长期以来，人们用常规三轴试验对M-C 准则进行适用性验证，但对真三轴试验验证较少。本文作者首先利用已有真三轴试验数据，讨论M-C 准则对岩土材料的适用性及局限性，并对M-C 准则进行修正，然后，提出基于真三轴试验数据的黏聚力c、摩擦角φ计算式，并以花岗岩为例验证该计算式的适用性。最后，考虑材料拉压强度差异修正拉压比K计算式。

1 M-C准则及真三轴试验验证

1.1 M-C准则

对于一般受力下的岩土材料，当以压应力为正时，其抗剪强度可用M-C准则表示为

式中：τ为材料极限抗剪强度；c为材料的黏结力；φ为材料的内摩擦角。

M-C准则可用主应力σ1和σ3表示为

π 平面极限迹线为强度准则极限面与π 平面的交线[12]，其方程为

式中：r(θσ)为π 平面极限迹线的矢径；g(θσ)为决定强度准则极限迹线在π 平面上变化规律的形状函数；rc为π平面上的三轴压缩强度矢长。

π 平面上M-C 准则可表示为式(3)所示形式，其形状函数为[13]

式中：θσ为罗德角；K为拉压强度比，

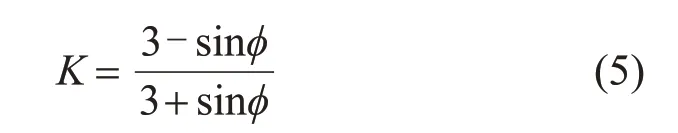
压缩强度矢长rc的表达式为

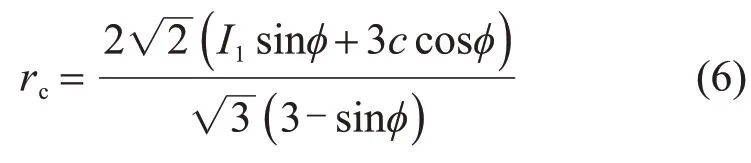
式中：I1为第一应力不变量，I1=σii=3p，p为静水应力。p与主应力σ1，σ2和σ3的关系为

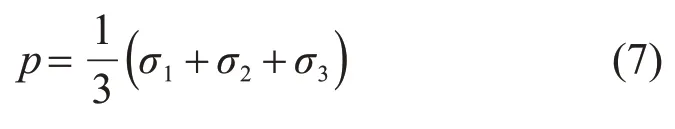
1.2 M-C准则真三轴试验验证

为验证M-C 准则在真三轴条件下的适用性，下面选取具有代表性的岩土材料即原状黄土、花岗岩、胶结砂与未固结砂的真三轴试验数据，对M-C 准则的适用性进行验证。具体方法为：1)将强度准则转化为式(3)所示形式；2)利用式(2)对真三轴压缩强度试验点进行数值拟合，求取c和φ；3)将2)中的c和φ及试验点对应的I1代入式(3)所示强度准则中，则可得到该I1条件下的强度准则极限迹线，将该I1条件下的极限迹线与试验点绘制于π平面上，即得到某一I1条件下强度准则与试验点的对比关系。

1.2.1 原状黄土

原状黄土是一种非饱和、结构性土，对水有其特殊敏感性。随着基础建设的进行，黄土的强度理论成为黄土地区工程建设的关键。下面选取文献[14]中原状黄土真三轴试验结果，对M-C 准则进行适用性验证，试验结果如表1所示。表1中，q为偏应力，

b为中间主应力比，b=(σ2-σ3)/(σ1-σ3)。M-C 准则、Matsuoka-Nakai(M-N)准则与原状黄土真三轴试验结果于π平面上的原状黄土强度对比关系如图1所示。由图1可知：M-N准则与M-C准则对原状黄土三轴压缩强度的预测在I1为600 kPa 和1 800 kPa时偏小，在I1为1 200 kPa 时偏大；对三轴拉伸强度预测时，M-N 准则与M-C 准则的预测值均偏小。由上述分析可知：M-C准则与M-N准则对原状黄土的适用性均有待加强。

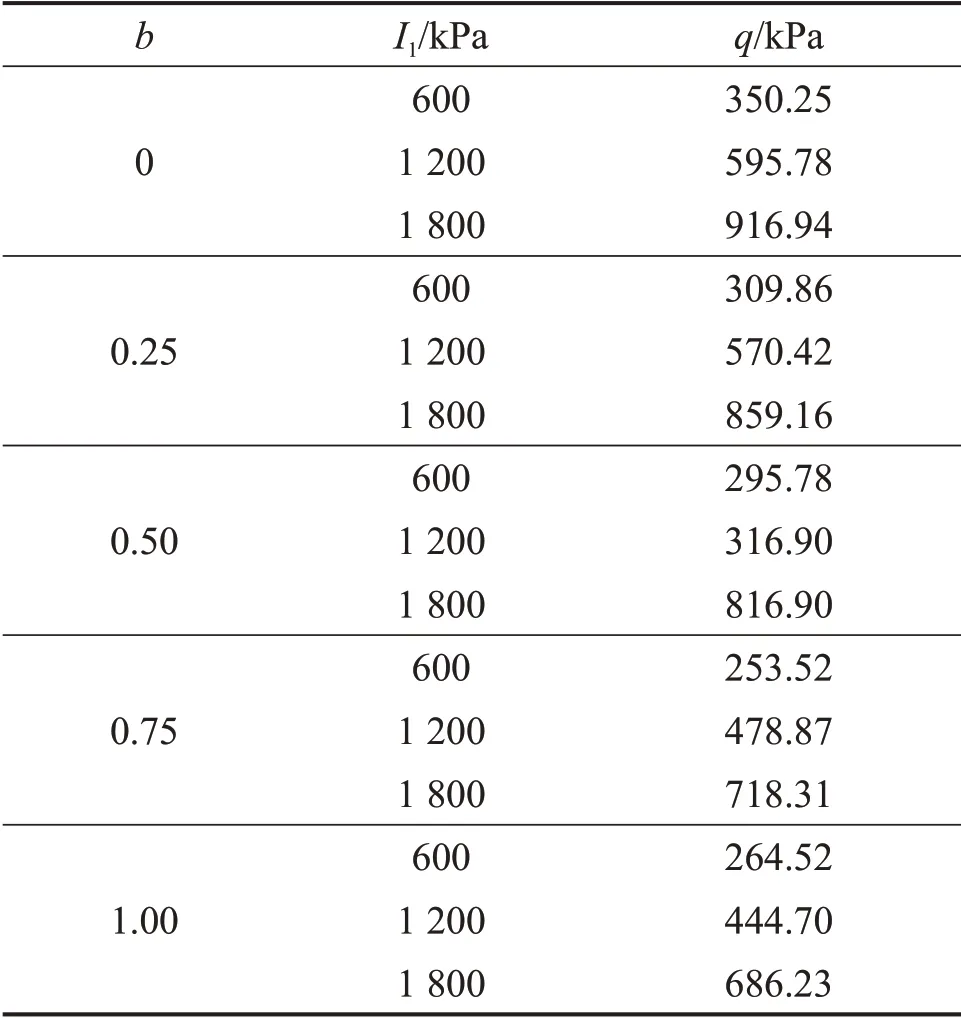
表1 原状黄土的真三轴偏应力试验结果Table1 True test results for stress for undisturbed loess kPa

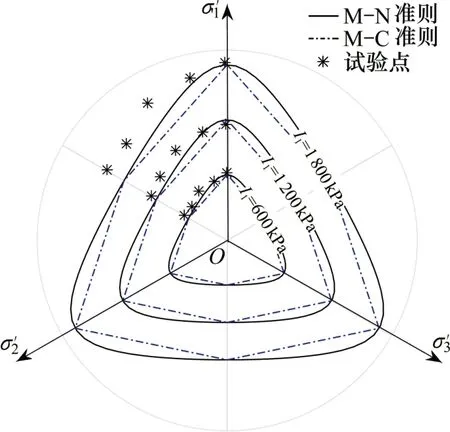
图1 准则对原状黄土强度的预测Fig.1 Strength prediction of undisturbed loess by criteria

1.2.2 花岗岩

花岗岩属于侵入岩，主要组成成分为石英与长石等矿物，具有强度高、耐磨损、颜色美观等特点，是一种重要的建筑材料与装饰材料。采用花岗岩真三轴试验结果[15]对M-C 准则实用性进行分析，结果见表2（其中，，为破坏点到静水压力轴的距离）。在不同I1条件下，M-C 准则、M-N 准则与花岗岩真三轴试验结果于π 平面上的对比关系如图2所示。由图2可知：M-N准则与M-C准则对三轴压缩强度的预测值在I1为303.73 MPa 和393.61MPa 时偏小，在I1为227.80 MPa 和485.04 MPa 时偏大；对三轴拉伸强度的预测值均小于试验值。相对而言，M-N 准则对花岗岩的适用性较强。

1.2.3 未固结砂与胶结砂

在岩土工程中经常遇到胶结砂与未固结砂的强度较低问题，人们对于这方面的试验研究较多，但对真三轴试验研究较少。选取胶结砂与未固砂的真三轴实验结果[16]对M-C准则适用性进行分析，结果见表3。在不同I1下，Lade-Duncan 准则(L-D准则)、M-N准则、M-C准则与未固结砂、胶结砂真三轴压缩强度试验结果于π平面上的对比关系分别如图3和图4所示。由图3可知：准则对未固结砂三轴压缩强度的预测结果均较好，但对于三轴拉伸强度的预测，随着I1增大，L-D准则预测结果与实际结果吻合度较高，M-C准则与M-N准则的预测结果与实际结果吻合度较低；相对而言，L-D准则对未固结砂的适用性较好。由图4可知准则对胶结砂三轴压缩试验值均有较好预测；对于三轴拉伸试验值的预测，随着I1增大，L-D准则的预测结果与实际结果吻合度较高，M-N准则与M-C准则预测结果吻合度较低；相对而言，L-D 准则对胶结砂的适用性较好。

表2 花岗岩的真三轴矢长试验结果Table2 True triaxial test results for stress for granite MPa

图2 准则对花岗岩强度的预测Fig.2 Strength prediction of granite by criteria

表3 未固结砂与胶结砂的应力试验结果Table3 True triaxial test results for uncemented and cemented sand kPa

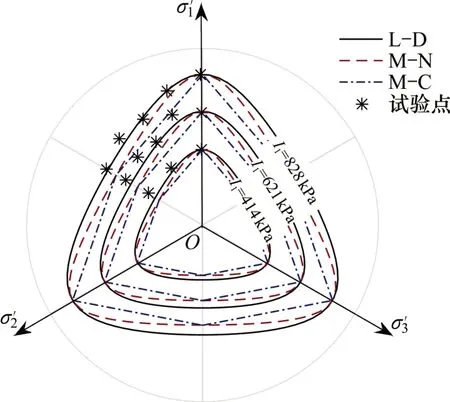
图3 准则对未固结砂强度的预测Fig.3 Strength prediction of uncemented sand by criteria

图4 准则对胶结砂强度的预测Fig.4 Strength prediction of cemented sand by criteria

通过对比研究可知：1)M-C 准则极限迹线为存在尖点的六边形，且只能在一定三轴压缩条件下与试验规律相符；2)M-C 准则极限迹线基本不经过三轴拉伸试验点，对三轴拉伸强度的预测性较差。综上可知，M-C 准则对材料的适用性尚有待提高。

2 M-C准则修正

为提高M-C 准则在真三轴条件下的适用性，并避免角点给数值计算带来困难，下面对其形状函数及K计算式进行适当修正。

2.1 形状函数g（θσ）的选取

形状函数的选取需符合以下条件[17]：

1)g(-π/6)=1，g(π/6)=K；

2)当θσ为-30°和30°时，dg(θσ)/dθσ=0；

3)当K=1 时，形状函数曲线为圆；当K=1/2时，形状函数图像形状由曲线变为直线，此时对应准则为M-C准则。

2.1.1 M-C准则形状函数特征

将式(4)在不同拉压强度比K下的曲线绘制在π平面中，所得结果如图5所示。由图5可知：M-C准则形状函数的曲线为不规则六边形，其下边界为正三角形，上边界为Tresca正六边形，且均在罗德角θσ=±30°时存在角点。

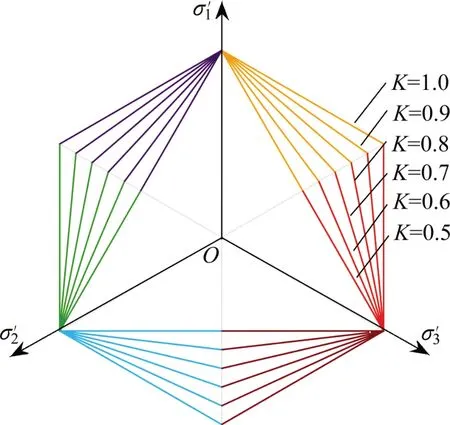
图5 K对M-C准则形状函数的影响Fig.5 Effects ofKon M-C criterion shape function

2.1.2 VAN EEKELEN形状函数中m的确定

VAN EEKELEN[18]提出了1 个光滑化的形状函数，其表达式为

式中：m为模型参数。易证该形状函数符合式(1)和(2)。下面讨论形状函数形状随模型参数m的变化规律及确定模型参数m，使该形状函数满足式(3)。

形状函数曲线随m的变化规律如图6所示。从图6可知：1)随着拉压强度比K增大，m的变化对形状函数形状的影响逐渐减弱；2)当K=0.5时，模型参数m对形状函数的形状的影响较大；3)当K=1时，模型参数m的变化对形状函数的形状无影响，为1个圆，因此，可确定拉压强度比K=0.5时的模型参数选取满足形状函数条件(3)，即确定了在K∈[0.5,1]时的形状函数模型参数。当K=0.5时，形状函数曲线随m的变化如图7所示。由图7可知：1)当模型参数m=-0.23 时，形状函数曲线与M-C准则曲线较接近；2)当模型参数m＞0 时，随着m增大，形状函数曲线逐渐靠近M-C 准则曲线；3)当模型参数m＜0时，随着m增大，形状函数曲线与M-C 准则曲线先逐渐靠近，当m=-0.23 时最接近；当m＞-0.23 时，随着m增大，形状函数曲线逐渐偏离M-C 准则对应的曲线，且产生畸变。综上所述，当模型参数m=-0.23 时，式(9)近似符合形状函数选取条件(3)，其他条件完全满足。当模型参数m=-0.23 时，形状函数式(9)随拉压强度比K的变化规律如图8所示。

图6 模型参数m对图形的影响Fig.6 Effects ofmon shape function

图7 k=0.5时，形状函数曲线随m的变化规律Fig.7 Effects of variousmon shape function whenk=0.5

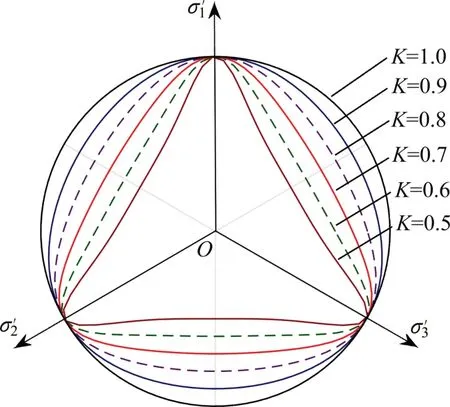
图8 K对形状函数的影响Fig.8 Effects of variousKon shape function

2.2 修正后M-C准则形式

通过形状函数替换，对M-C 准则进行修正，修正后的准则形式为

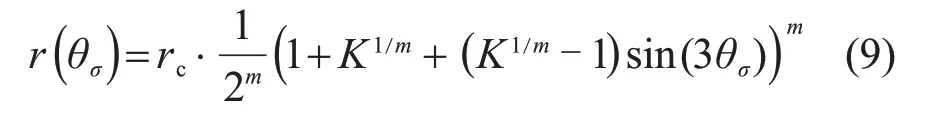
式中：m=-0.23；rc由式(6)定义并计算。

2.3 修正准则相关参数确定

2.3.1 数值试验p*-q*关系的确定

OHMAKI[19]采用一种坐标平移的方法，可实现“变换应力空间”，转化后的p*和q*与p和q的关系为

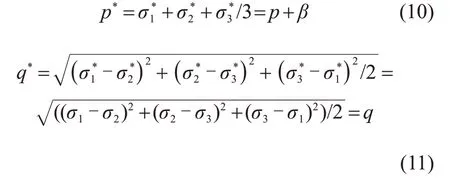
式中：p*和q*分别为变换应力空间后的静水应力与剪切力。

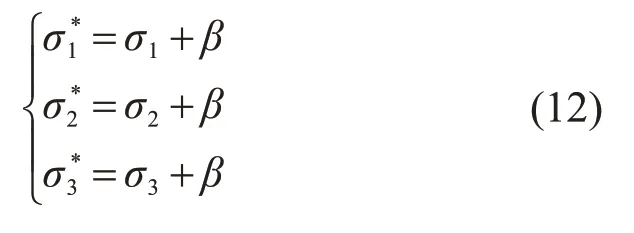
其中：β为考虑材料黏结特性的参量，其值等于或接近于材料拉伸强度σt，具体计算方法及步骤见文献[20]。当β=0 时，材料为无黏结特性材料；当β≠0时，材料为黏结特性材料。黏结特性材料转化为无黏结特性材料，相当于沿静水应力轴负方向平移了(β，β，β)。

已知在低应力下主应力空间三维破坏面为曲面，在高应力下为线性直线[21]，据此推测，p*和q*满足幂函数方程：

式中：pa取值为100 kPa；μ和n分别为受材料黏结性质及静水应力影响的强度参数。通过坐标变换，可将黏结特性材料转化为无黏结特性材料，从而使求解得到简化。坐标平移方法及式(13)中相应参数变化对子午面失效曲线的影响如图9所示。

图9 参数n，pa，μpa，β对子午面失效曲线的影响Fig.9 Failure curves in meridian plane and interpretation ofn，pa，μPa，β

2.3.2 材料参数μ和n的确定

将式(13)进行变换，有

对式(14)两边同时取对数可得

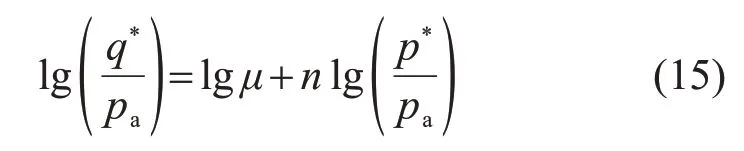
将试验值线性拟合lg(q*/pa)和lg(p*/pa)，可得基于试验的μ和n，拟合结果如图10所示。由图10可知：n为拟合直线的斜率，lgμ为截距。需注意的是：为了较好地拟合出相应参数，一般至少需3组三轴试验结果。

图10 参数μ和n在对数坐标中的确定Fig.10 Determination of strength parametersμandnin logarithmic coordinate diagram

2.3.3 拉压强度比K的确定

若已知材料的拉伸强度矢长rt和压缩强度矢长rc，则拉压强度比K可定义为[12]

偏应力q与r(θσ)的关系为

联立式(13)，(16)与式(17)可得修正的K计算式为

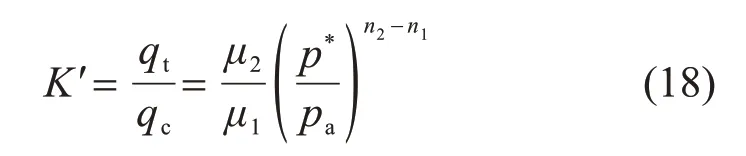
式中：μ1和n1为拟合三轴压缩试验点所得强度参数；μ2和n2为拟合三轴拉伸试验点所得强度参数。

3 基于试验的材料参数c和φ的计算方法

M-C准则用剪应力q与静水应力p可表示为[14]

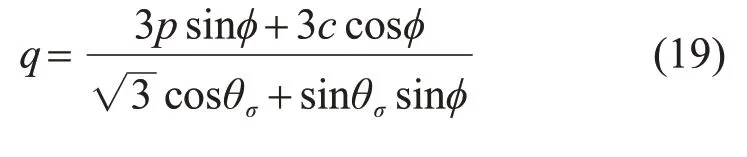
当θσ=-30°时，σ1≥σ2=σ3，式(19)可写成如下形式：

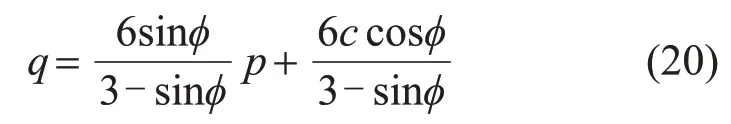
此时，M-C准则切线斜率可表示为

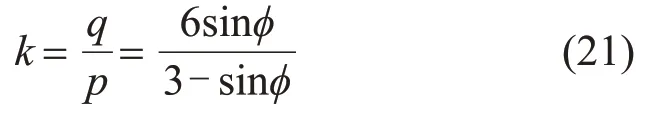
对式(21)进行变换，可得内摩擦角φ的计算式为

由于q*与p*存在一一对应关系，因此，对式(13)求导可得任意位置下幂函数的切线斜率为

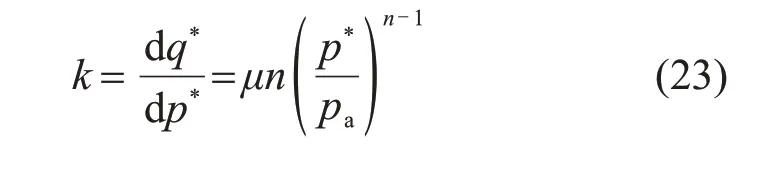
将式(23)代入式(22)，可得基于试验结果的内摩擦角φ计算式：

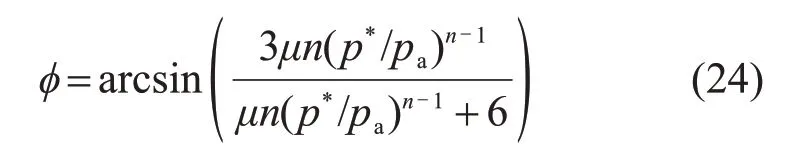
由式(24)可知：随着静水应力p*增大，内摩擦角φ逐渐减小；当p*达到一定值时，φ近似为0，材料强度达到“平台期”[22]。计算出φ后，将式(13)与式(24)代入式(20)，可得黏结力计算式：

依据岩土材料性质，黏结力取值区间为c≥0，再根据式(25)进行分析可知强度参数n的取值范围为n∈(0,1]。在计算过程中，当n=1 时，黏结力c=0，材料无黏结特性；当n∈(0,1)时，随着静水应力p*增大，黏结力c逐渐增大；当出现n＞1的情况时，依据式(25)及黏结力取值区间，需取n=1，即进行线性拟合求解。由式(24)与式(25)知，修正后的c和φ计算式为静水应力p*的函数。

4 修正强度准则的真三轴试验验证

下面利用第2 节中的试验结果、修正前后MC 准则于π 平面进行对比分析。在试验验证过程中，rc由式(6)计算，且不考虑c和φ的变化；拉压比K由式(18)计算，强度参数由式(13)计算，计算步骤见2.3.2节。

4.1 原状黄土

原状黄土K计算所需强度参数见表4，不同I1下的rc与K见表5。黄土类土的抗拉强度一般假定为0[23]，因此，β=0 kPa。原状黄土与M-C 准则修正前后的对比见图11。由图11可知：修正后M-C准则极限迹线的变化规律与原状黄土试验点变化规律相符；整体预测上，当I1=1 200 kPa 时，修正后M-C 准则预测值略偏大；当I1为600 kPa 和1 800 kPa时略微偏小。

表4 原状黄土K计算所需的强度参数Table4 Strength parameters required for undisturbed loessKcalculation

表5 原状黄土的rc与KTable5 rcandKfor undisturbed loess

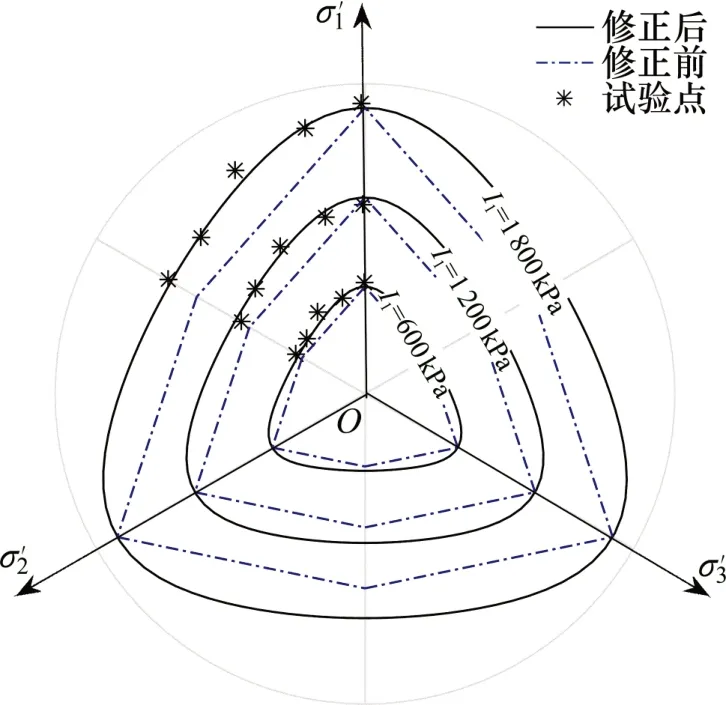
图11 修正后准则对原状黄土强度的预测Fig.11 Strength prediction of undisturbed loess by modified criteria

4.2 花岗岩

表6所示为花岗岩K计算所需强度参数，在计算过程中，β=10 MPa (根据文献[20]中方法计算，其余材料相同)，p*=p+β。不同I1条件下的rc与K见表7。M-C准则修正前后与试验点于π平面的对比如图12所示。由图12可知：花岗岩试验点的强度变化规律与修正后M-C 准则的相符；当I1为227.80 MPa 和485.04 MPa 时，花岗岩试验点基本落在修正后M-C 准则极限迹线上，准则对试验点的预测结果非常好；当I1为303.73 MPa 和393.61 MPa 时，修正后M-C 准则对试验点的预测结果整体上略偏小。

表6 花岗岩K计算所需的强度参数Table6 Strength parameters required forKcalculation of granite

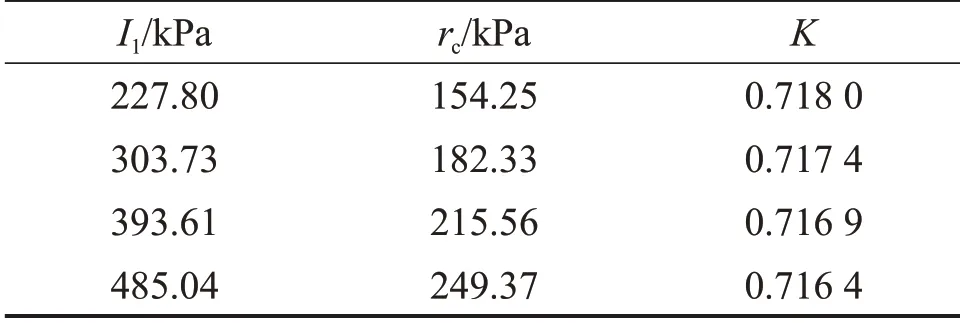
表7 花岗岩的rc与KTable7 rcandKfor granite

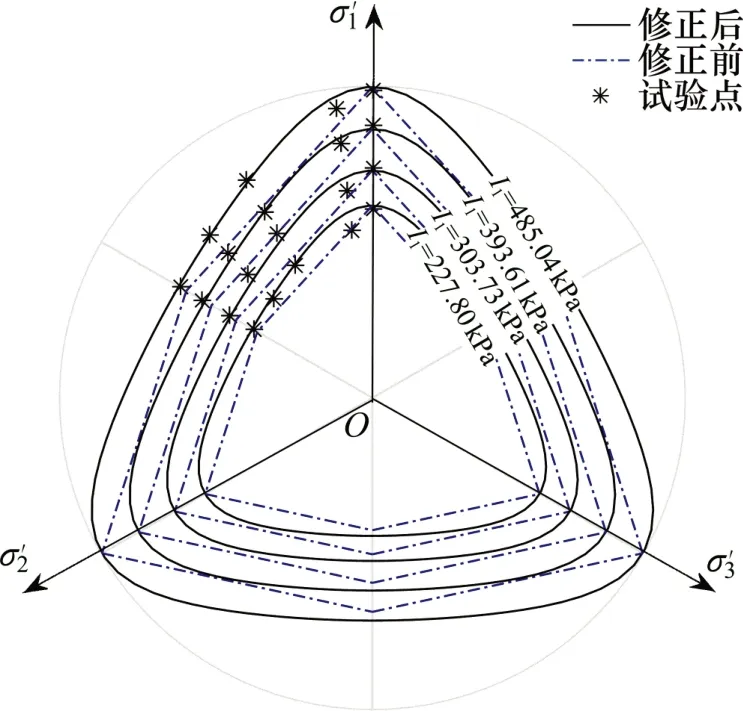
图12 修正后准则对花岗岩强度的预测Fig.12 Strength prediction of granite by modified criteria

4.3 胶结砂与未固结砂

胶结砂与未固结砂中K计算所需强度参数如表8所示。在计算过程中，未固结砂β=0 kPa，p*=q；胶结砂β=10 kPa，p*=p+β。未固结砂拟合强度时，出现n＞1，取n=1进行拟合，原因见式(25)；不同I1条件下的rc与K如表9所示。在不同I1条件下，M-C 准则修正前后与试验点于π 平面的对比结果见图13和图14。从图13可见：胶结砂试验点基本上落在修正后M-C准则极限迹线上，修正后M-C准则对胶结砂的适用性较好。由图14可知：修正后M-C 准则较修正前对未固结砂试验点的预测有了明显提高，试验点基本落在准则极限迹线上或附近；但对三轴拉伸强度预测时，I1为828 kPa 时略微偏大，I1为414 kPa和621 kPa时略微偏小，预测结果基本准确。

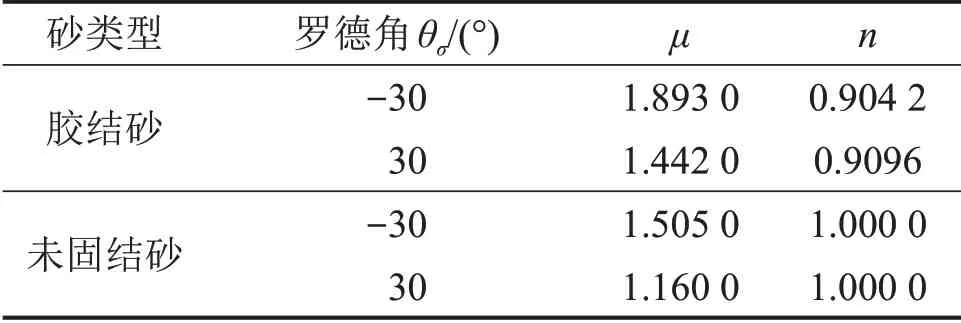
表8 胶结砂与未固结砂K计算所需的强度参数Table8 Strength parameters required for calculation of cemented and unconsolidated sand K

表9 胶结砂与未固结砂的rc与KTable9 rcandKfor cemented and uncemented sand

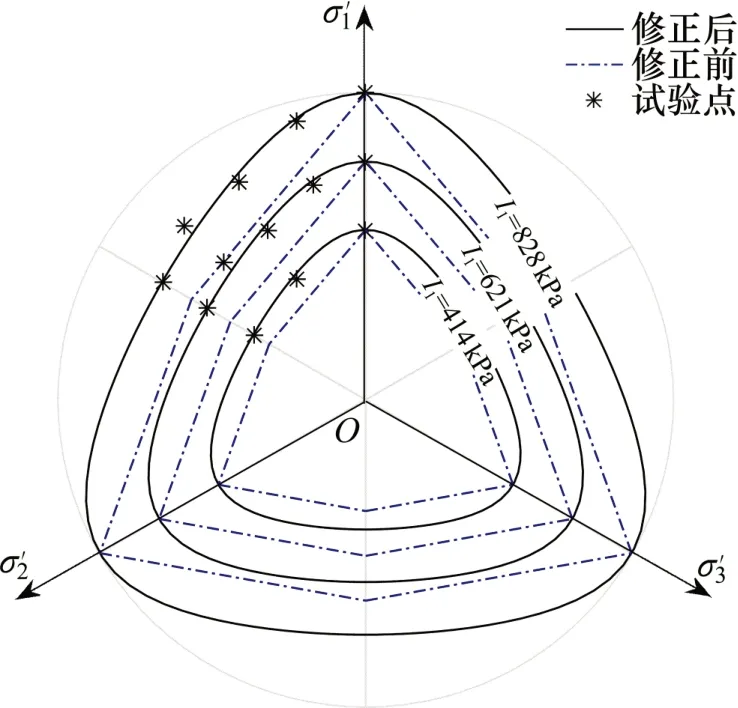
图13 修正后准则对胶结砂强度的预测Fig.13 Strength prediction of cemented sand by modified criteria

利用第2 节中真三轴试验数据与修正前M-C准则的对比分析结果，检验修正后M-C 准则的适用性，主要结论如下。

1)试验点基本落在修正后M-C 准则极限迹线上或附近，修正后M-C准则对材料的适用性较好。修正后M-C 准则与修正前相比，准则极限迹线随θσ的变化不再呈线性变化，与试验点变化规律相符，且能够较好地预测材料三轴拉伸强度。

2)未考虑c和φ随p(或p*)变化的修正后M-C准则，在三轴压缩强度的预测上依旧存在偏差，致使修正后M-C准则对试验点预测整体存在偏差，如对原状黄土与花岗岩的三轴压缩强度的预测值。

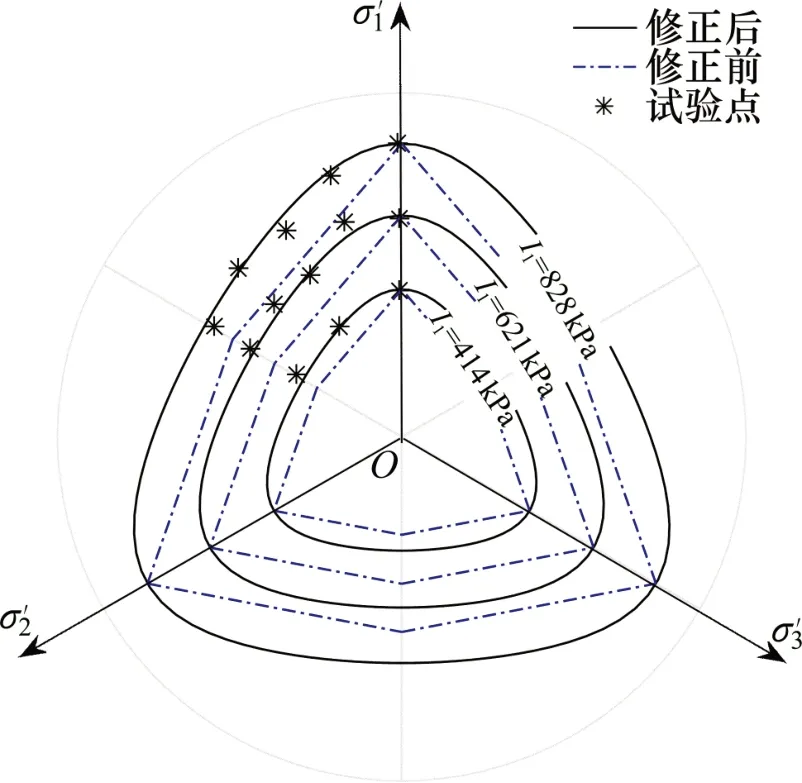
图14 修正后准则对未固结砂强度的预测Fig.14 Strength prediction of uncemented sand by modified criteria

3)在K计算过程中，非线性(n1，n2∈(0,1)时)拟合参数计算所得结果精度高于线性(n1=n2=1时)拟合计算结果精度，即非线性拟合优于线性拟合。

5 相关量计算可靠性验证

由前述分析可知，修正后M-C 准则比修正前适用性更好，但在三轴压缩强度的预测上与修正前的相同，致使修正后M-C 准则对试验点的预测依然存在偏差。下面利用式(24)与式(25)讨论c和φ的变化规律，并代入式(6)计算rc，讨论动态参数计算的适用性。随后，将式(18)计算的K′与修正的L-D准则、峰值比法及试验所得K进行对比分析，讨论式(18)对拉压比计算的适用性。下面以花岗岩为例来进行说明。

5.1 材料参数变化规律及本文计算方法的可靠性

在不同I1条件下，由式(24)与式(25)计算的c和φ见表10。由表10可知：随着I1增大，c逐渐增大，φ逐渐减小，均不为定值。将表10中c和φ代入式(6)计算rc，并与试验所得rc以及M-C准则中rc进行比较，结果表明：利用表10中c和φ计算的rc与试验rc基本一致，从而证实了动态参数计算的适用性。需注意的是，在rc计算过程中，新方法中I1需由I*1=I1+3β替换。考虑c和φ变化后，修正后MC 准则与花岗岩试验点于π 平面的对比结果见图15。由图15可知此时修正后M-C准则对试验点的预测结果很好，同时也说明rc随p(或p*)的变化呈非线性，在准则修正过程中需予以考虑。

表10 动态参数的计算及rc的预测Table10 Prediction of dynamic parameters and calculation ofrc

图15 考虑参数变化的修正后准则对花岗岩强度的预测Fig.15 Strength prediction of granite based on modified parameters after parameter variation

5.2 拉压强度比计算精度的比较

为验证本文拉压强度比计算方法的精确性，利用式(18)预测修正的L-D准则及峰值比法预测K与试验所得K进行对比分析。

5.2.1 修正的L-D准则（简称修L-D）

为提高L-D准则对材料的适用性，LADE[23]建议一种修正的L-D准则：

式中：m和η为材料参数；

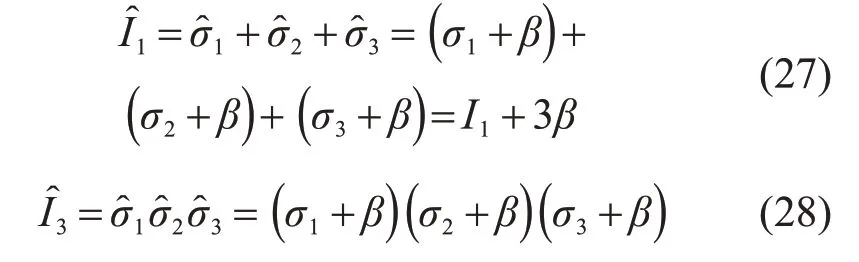
重新整理式(26)得

其中：

对式(26)两边同时取对数，得

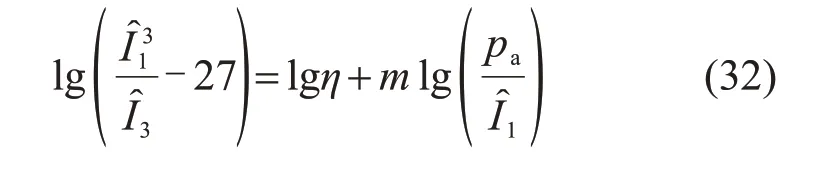
5.2.2 峰值比法

在对粉细砂的研究中，通过引入形状函数g(θσ)，得到一般应力下的M-C准则[24-25]为

式中：峰值应力比Mf=6 sinφ/(3-sinφ)；当应力条件以压为正时，g(θσ)取为

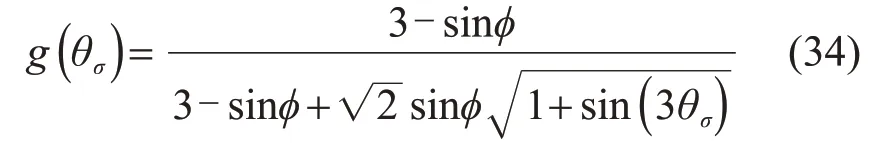
扈萍等[25]采用的办法为：考虑材料拉压强度的差异性，直接采用三轴拉伸与三轴压缩时的峰值应力比的比值定义拉压强度比K，计算式为

当θσ=-30°时，由式(34)有g(θσ)=1；代入式(33)可得

对比式(19)及考虑粉细砂黏结力为0 MPa，易知Mf为剪应力q与静水应力p线性拟合直线的斜率，峰值比法定义的K即为线性拟合三轴拉伸试验点与三轴压缩试验点所得直线斜率的比值。利用峰值比法，线性拟合花岗岩三轴拉伸试验点与三轴压缩试验点可得直线斜率分别为：k1=0.969 6，k2=1.359 0，K=k1/k2=0.713 5。

5.2.3 计算结果比较

为验证式(18)对拉压强度比预测的精确性，将修正的L-D准则与峰值比法预测K、式(18)预测与试验所得K进行对比分析，各计算方法所得结果如表11所示。由表11可知：由式(18)预测的K与试验所得K基本一致，且变化规律相符；峰值比法预测的K虽然与试验所得K偏差较小，但该值在任意I1下为定值，与试验值的变化规律不符；修正的LD准则预测的K明显低于试验所得K，且预测值的变化规律与试验值变化规律相反，对试验值的预测性较差。由上述分析可知，考虑材料拉压强度差异的非线性计算方法(式18)对试验所得K有较好的预测效果，计算结果更可靠。