单向循环荷载作用下饱和重塑红黏土的动力特性

罗文俊，王海洋，马斌，陈晓飞

(1.华东交通大学 土木建筑学院，南昌 330013；2.中铁二局集团有限公司，成都 610000)

红黏土是一种呈棕红、褐黄等色的特殊黏性土，在江西、湖南、广西等湿热多雨地区皆有广泛分布。随着铁路交通事业的飞速发展，很多地段都需要用红黏土作为路基填料，红黏土具有弱膨胀性、压缩性低、结构连接强度高的特点，用作铁路路基填料可以带来很高的经济效益[1]。近年来，铁路逐渐向高速、重载方向发展，在长期循环荷载作用下，红黏土路基产生变形和不均匀沉降，严重影响了列车运行的安全性和舒适性。因此，研究循环荷载作用下红黏土的动变形、动孔压特性具有重要意义。

通过动三轴试验研究土体动力特性是岩土领域普遍采用的方法[2-3]。多年来，学者对于红黏土动力特性的研究已经取得了一些进展。李志勇等[4]为了研究湘南地区红黏土的动态回弹性能，通过动三轴试验发现，动态回弹模量与围压、压实度呈正相关，与偏应力呈负相关，土体处于最优含水率时动态回弹模量值最大；穆坤等[5]对广西原状红黏土进行了循环加载动三轴试验，分析了红黏土的动应力-动应变关系及固结应力比、围压、含水率等对动弹性模量和阻尼比的影响；Fall等[6]通过循环加载三轴试验，研究了红黏土不排水条件下的动变形特性；昌思[7]对洞庭湖区饱和原状粉质黏土的动变形特性进行了试验研究，得出了动应力幅值、围压、固结比和加载频率对累积塑性应变的影响规律，并建立了累积塑性应变模型。然而，红黏土作为路基填料扰动性很大，且红黏土的动力特性受地域差异和应力历史的影响也很大，目前，对江西红黏土动力特性的研究相对缺乏，因此，对江西重塑红黏土做进一步试验研究显得尤为重要。

笔者针对江西饱和重塑红黏土进行了动三轴试验研究，分析了动应力比、初始孔隙率、固结围压、加载频率、排水条件对红黏土塑性累积应变和动孔压的影响规律。

1 饱和重塑红黏土的振动三轴试验

1.1 试验仪器

试验在高精度动三轴仪上进行，试验系统由驱动装置、压力室、围压/反压控制器和信息采集仪等部分组成，见图1。试验过程由电脑控制，通过内置的GDSLAB软件来设置试验参数并记录试验数据。该设备可提供最大轴向激振荷载4 kN；压力室承受的最大围压为2 MPa；应变测量精度为10-4；循环加载频率范围0～2 Hz，加载波形可以选择正弦波、方波、三角波和梯形波，也可以自定义加载波形，每个加载周期可以记录多达100个数据点；试验控制方式分为应力控制和应变控制。

图1 动三轴试验系统Fig.1 Dynamic triaxial test

1.2 土样的基本物理参数及试样制备

试验所用土样取自南昌市孔目湖边在建32号土建实验楼旁的残积红土层，为保证土样的均一性，采用重塑土制样。将土样风干后用木碾碾碎，过2 mm土工标准筛。试验测得红黏土的最大干密度为1.74 g/cm3，最优含水率为16%，击实曲线见图2。依据《公路土工试验规程》[8]对试验土样进行了一系列基础物理试验，红黏土的基本物理参数见表1。重塑土的制样方法有泥浆固结法和分层湿捣法，根据试验方案，采用后者较为便捷。用最优含水率拌和土样，在特制的击实器中分5层击实制样，制得的圆柱体试样尺寸为φ50 mm×100 mm。严格控制每层土的质量，为避免制得试样出现分层现象，在击实后层与层之间用切土刀刮毛。试样制备好后放入真空饱和缸中抽气饱和，抽气负压0.1 MPa，抽气时间2 h，饱和时间10 h以上，然后进行振动三轴试验。

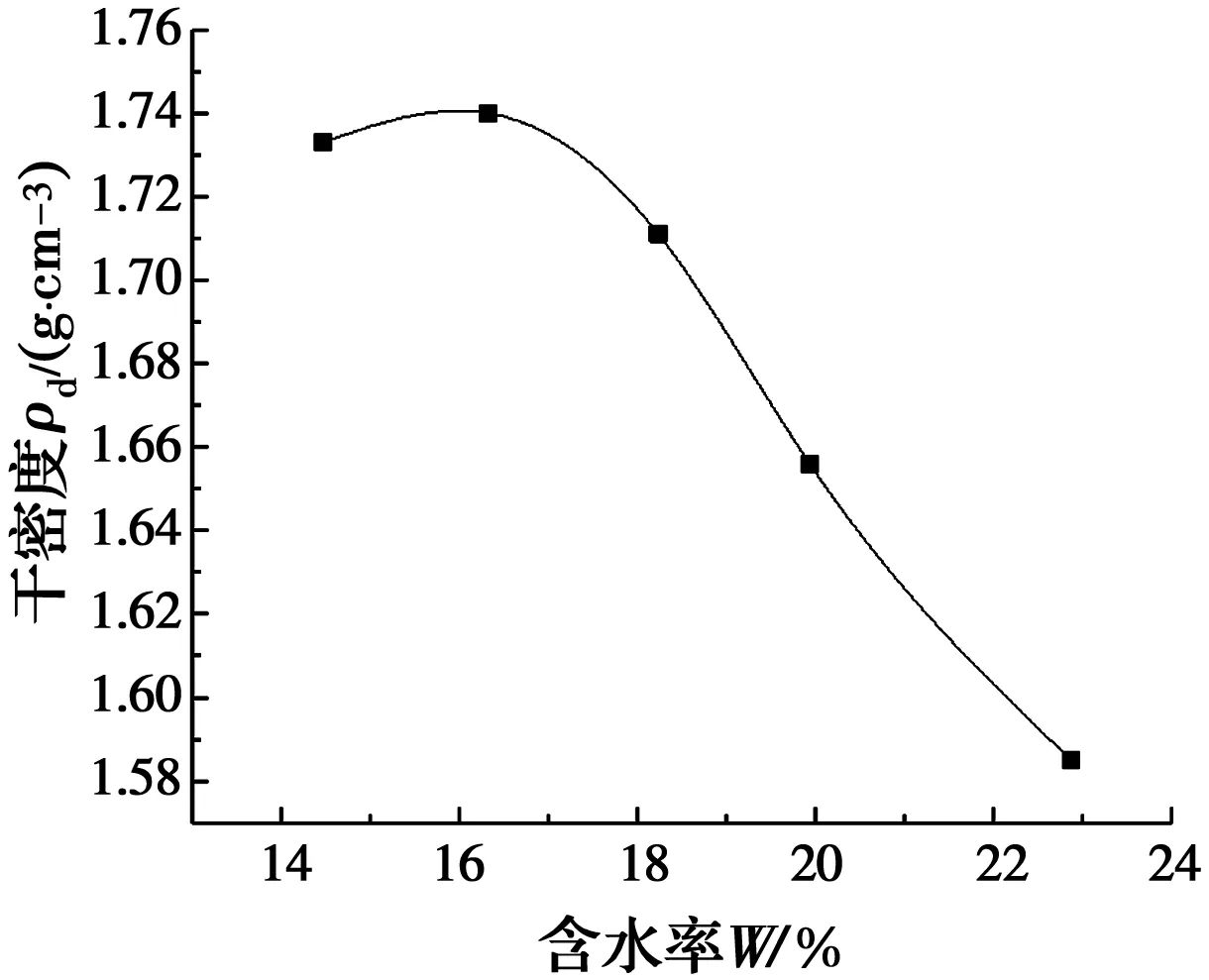
图2 ρd-w关系曲线Fig.2 ρd-w relation curve

表1 红黏土基本物理指标
Table 1 Basic physical indexes of red clay

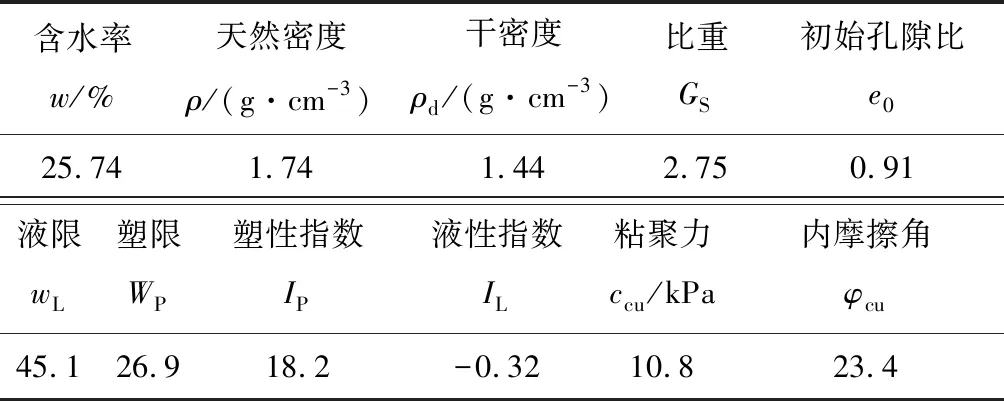
含水率w/%天然密度ρ/(g·cm-3)干密度ρd/(g·cm-3)比重GS初始孔隙比e025.741.741.442.750.91液限wL塑限WP塑性指数IP液性指数IL粘聚力ccu/kPa内摩擦角φcu45.126.918.2-0.3210.823.4

1.3 试验方案设计

列车荷载作用时间长，振动频率低，其引起的动应力是一种近似正弦曲线的单向脉冲模式，只对路基土体产生压缩[9-11]，故试验采用应力控制式单向加载方式，加载波形选用正弦波，每个循环周期采集20个数据点。试样在真空饱和缸中抽气饱和后，在动三轴仪上稍加反压即可达到规范要求的饱和度，经B检测得到试样的饱和度为97%。然后，在设定的围压下进行等向排水固结，试验前在试样周围贴6～8条滤纸条以加速排水固结[12]，待超孔隙水压力完全消散，等于所施加的反压值时，表明固结完成。固结完成后施加单向循环荷载(单向压缩)，进行动力试验。试验加载过程如图3所示。

图3 正弦单向应力控制加载过程Fig.3 Sinusoidal unidirectional stress control loading process

共进行了15组饱和重塑红黏土动三轴试验。试验过程充分考虑了试样初始孔隙率、固结围压、动应力比、加载频率和排水条件等综合因素对土体应变及孔压的影响，共制得3种不同初始孔隙率的试样，分别为0.65、0.7、0.75；固结围压采用50、100、200、400 kPa；定义动应力比R=σd/2σ3(σd为作用在试样上的动偏应力，σ3为固结围压)，分别取0.2、0.25、0.3、0.4；根据已有监测结果显示，列车运行时引起的垂向路基土体响应频率的区间范围在0.4～2.6 Hz之间[13]，试验采用的加载频率为0.5、1.0、2.0 Hz，荷载循环次数为5 000次。不排水试验的孔隙水压力从试样底部测得。详细试验方案见表2。

表2 动三轴试验方案Table 2 Dynamic triaxial test scheme

2 试验结果分析

试验采集的数据点众多，为便于处理和分析，只选取循环振次N=1、5、10、20、40、60、80、100、150、200、300、400、600、1 000、1 500、2 000、3 000、4 000、5 000所对应的数据进行整理和分析，得出不同影响因素下试样塑性累积应变和动孔压比随循环振次的变化规律。

2.1 循环荷载作用下塑性累积应变的影响因素分析

2.1.1 动应力比的影响 为了研究动应力比大小对试样塑性累积应变的影响规律，在400 kPa固结围压下对同一试样进行了4种动应力比的不排水试验，图4为此试验条件下试样的塑性累积应变εp与循环振次N的关系曲线图。

由图4可知，动应力比的大小对试样的塑性累积应变影响很大。从图中累积应变随荷载循环次数的发展形态来看，可以将其分为3种类型，即稳定型、临界型和破坏型。临界型曲线所对应的动应力比即为临界动应力比。当动应力比大于临界动应力比时，试样在很小的循环次数内即发生破坏，其塑性累积应变曲线发展迅猛(如图中动应力比为0.4的情形)；当动应力比小于临界动应力比时，累积应变在加载初期迅速增加，然后曲线出现拐点并衰减，最后逐渐趋于稳定，即试样产生塑性硬化。现实生活中，列车在高速运行时，传递给路基土体的动荷载作用时间长，循环次数多，动应力一般小于路基土体的临界动应力[14]。因此，笔者主要研究动应力比小于临界动应力比的情况。

图4 不同动应力比下累积应变随循环振次的变化曲线Fig.4 Curves of cumulative strain with cyclic vibration times under different dynamic stress ratios

2.1.2 初始孔隙率的影响 图5为3种不同初始孔隙率的试样在动应力比0.3和固结围压100 kPa下塑性累积应变随荷载循环次数的变化规律。可以看出，在试验加载初期，3种试样的累积应变均迅速增加，随着循环次数的不断增大，应变衰减并逐渐趋于平缓。在相同的循环振次下，初始孔隙率越大的试样产生的塑性累积应变越大，这是因为初始孔隙率大的试样密实度相对较小，抗剪强度低，在相同的动应力下就会产生较大的塑性变形。由图5还可以发现，初始孔隙率越大的试样，其累积应变曲线拐点出现越滞后。初始孔隙率0.65的试样累积应变曲线拐点出现在循环振次150次，初始孔隙率0.7的试样累积应变曲线拐点出现在循环振次300次，初始孔隙率0.75的试样累积应变曲线拐点出现在循环振次400次左右。

图5 不同初始孔隙率下累积应变随循环振次的变化曲线Fig.5 Curves of cumulative strain with cyclic vibration times under different initial

2.1.3 固结围压的影响 图6为初始孔隙率0.65的试样在相同动应力比不同固结围压下的塑性累积应变随荷载循环次数的发展曲线。由图6可以看出，3种围压下，试样的累积应变随着循环振次的增加均表现出起始快速增长，后增长率减小，并逐渐趋于平稳的特征，在相同的循环振次下，围压越大，试样产生的塑性累积应变越大，这可以通过动应力比的定义来解释，动应力比R=σd/2σ3，当动应力比一定时，围压越大，作用在试样上的动偏应力就越大，那么对于相同密实度的试样来讲，就会产生较大的塑性应变；同样可以发现，产生塑性应变越大的试样，其应变曲线拐点的出现越滞后。

图6 不同固结围压下累积应变随循环振次的变化曲线Fig.6 Curves of cumulative strain with cyclic vibration times under different consolidation confining

2.1.4 加载频率的影响 图7为固结围压为100 kPa，试样轴向作用动应力比为0.3时，在加载频率0.5、1.0、2.0 Hz作用下，试样的不排水塑性累积应变随荷载循环次数的变化曲线。由图7可以看出，在不同加载频率作用下，饱和重塑红黏土的塑性累积应变变化趋势是一致的，随着荷载循环次数的不断增大，塑性累积应变均表现为一开始快速增大，后趋于平稳；加载频率越小，试样达到稳定时的塑性累积应变越大，究其原因，在较小的振动频率下，饱和红黏土可吸收较大的能量，其动强度和阻尼比也较小[15]，此时试样抵抗振动变形的能力较差，因而会随着循环振次的增加产生相对较大的累积应变。

图7 不同加载频率下累积应变随循环振次的变化曲线Fig.7 Curves of cumulative strain with cyclic vibration times under different loading frequencies

2.1.5 排水条件的影响 图8为不同排水条件下饱和重塑红黏土塑性累积应变大小的对比图。显然，无论是否排水，循环荷载作用下轴向累积应变都随着循环振次的增加而增大，增大速率随着振次的增加有所衰减，最终趋于稳定。在其他条件相同的情况下，试样在不排水条件下产生的塑性累积应变大于排水条件下产生的塑性累积应变，随着动应力比的增大，试样的累积应变也越大，这种变形大小的差异也越大。造成这种差异的原因在于试样在不同排水条件下，轴向累积应变产生的机理不同。在不排水条件下，试样不产生体应变，其轴向累积应变的产生只是因竖向动偏应力而引起的，不同的是，在排水条件下，试样轴向累积应变的产生除了竖向动偏应力的作用外，还与孔压消散引起的体应变有关[16]。在较高的动应力比下，不排水时，试样在循环加载过程中会产生较大的超孔隙水压力，造成试样极度软化，从而产生很大的塑性变形甚至破坏；而此时排水情况下，伴随着试样中水分的缓慢排出，土体逐渐变得密实，强度有所提高。因此，排水条件下试样的累积形变量会小于不排水条件下试样的累积形变量。

图8 不同排水条件下累积应变随循环振次的变化曲线Fig.8 Curves of cumulative strain with cyclic vibration times under different drainage conditions

图9为排水条件下，不同动应力比对试样体应变的影响曲线。与动应力比对试样塑性累积应变的影响规律一致，在相同的动应力比下，试样的体应变随着循环振次的增加而不断增大；在相同的荷载循环作用次数下，动应力比越大，试样产生的体应变越大。

明确发展导向，扎实推进“六个高质量”。省委明确提出，把高质量发展作为江苏未来一个时期最鲜明的导向，力争在高质量发展上走在全国前列。在具体工作中，重点推进经济发展高质量、改革开放高质量、城乡建设高质量、文化建设高质量、生态环境高质量、人民生活高质量。召开全省科学技术奖励大会暨科技创新工作会议，大力推进创新驱动发展战略，深化科技体制机制改革，努力实现关键核心技术自主可控，为推动高质量发展走在前列注入磅礴的科技动力。把建设现代综合交通运输体系作为七项重点任务之一，有针对性地解决好各类交通最突出的问题，实现交通基础设施的互联互通、相互支撑。

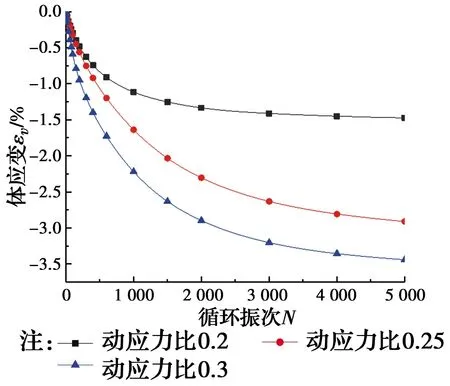
图9 体应变随循环振次的变化曲线Fig.9 Variation curve of body strain with cyclic vibration times

2.2 滞回曲线分析

滞回曲线可以很好地反映土体在循环加载过程中的应力-应变关系，通过对滞回曲线线形形态的分析，可以从侧面反映出土体强度的发展状况。依据试验结果，得出了试样在不同动应力比条件下的应力-应变滞回曲线，由于试验结果排水条件对滞回曲线的发展规律影响不大，只作出了试样在不排水条件下的应力-应变滞回曲线图，如图10(a)、图11(a)、图12(a)。为了更直观地分析不同循环振次下滞回曲线的形态变化，作出部分循环振次下的滞回曲线，并省略掉产生的累积应变，让不同循环振次下的滞回曲线都从原点出发，得到图10(b)、图11(b)、图12(b)。

图10 动应力比为0.2时不排水条件下偏应力-轴向应变 关系曲线Fig.10 Deflection stress-axial strain curve under undrained condition when dynamic stress ratio is

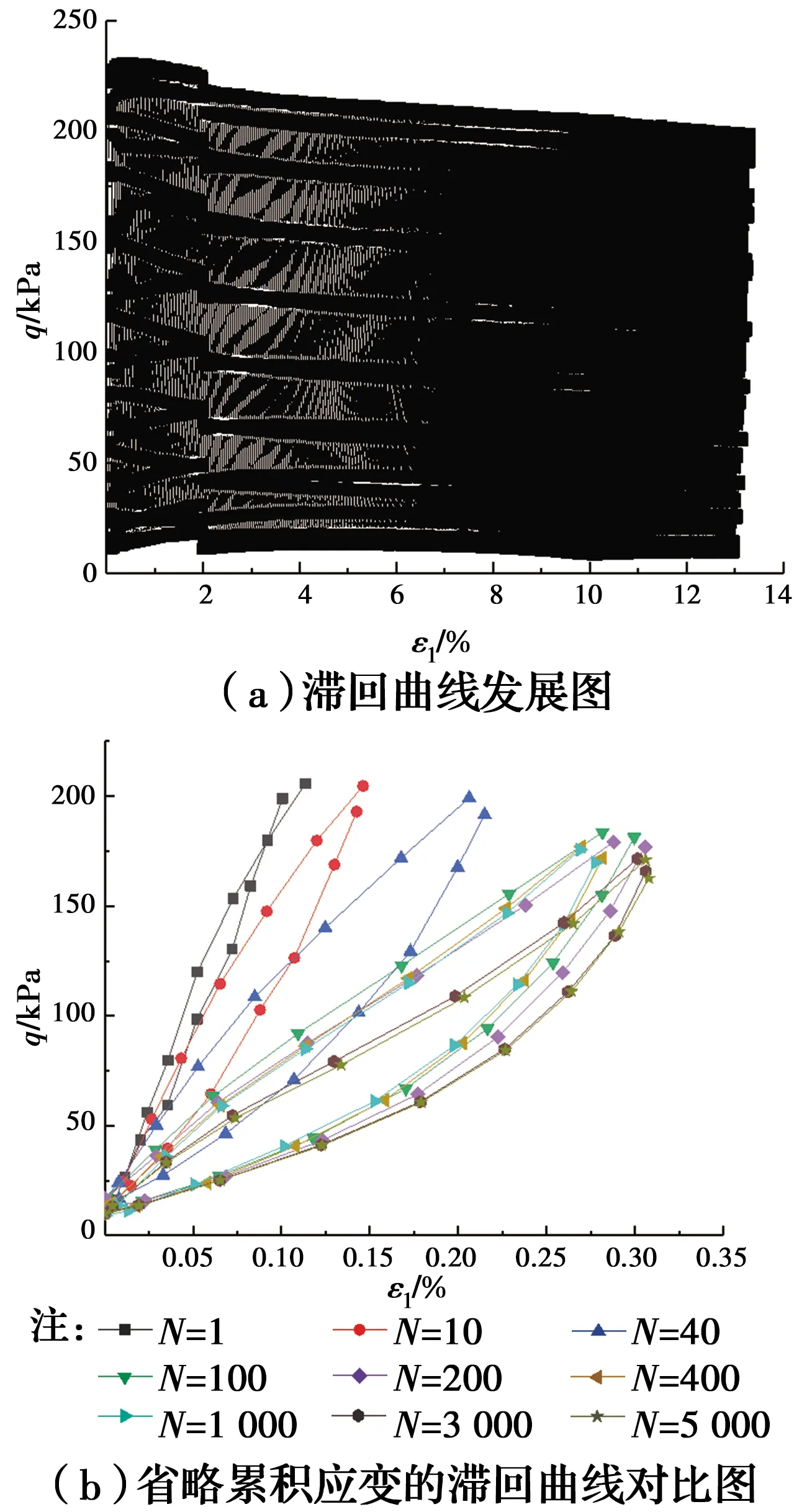
图11 动应力比为0.25时不排水条件下偏应力-轴向 应变关系曲线Fig.11 Deflection stress-axial strain curve under undrained condition when dynamic stress ratio is 0.25

图12 动应力比为0.3时不排水条件下偏应力-轴向应变 关系曲线Fig.12 Deflection stress-axial strain curve under undrained condition when dynamic stress ratio is

从图10(a)、图11(a)、图12(a)可以看出，偏应力-轴向应变关系曲线表现为一系列封闭的滞回圈。试验加载初期，滞回曲线分布较为稀疏，后期则较为密集，说明试验加载初期试样累积应变增加迅速，后期逐渐达到稳定。在动应力比为0.2时，随着应变的不断累积，滞回圈略有拉长并偏向轴向应变一侧倾斜，单个循环周期内滞回圈的面积也有所增大，随着动应力比的增大，试样轴向累积应变也不断增大，应力-应变滞回圈的这种变化也愈加明显，倾斜程度和面积都越来越大，说明较大的动应力比增大了土体的软化程度。但如图10(b)、图11(b)、图12(b)所示，3 000次与5 000次循环下的滞回曲线几乎重合，说明在较大的循环振次下，土体的应变软化程度减弱了。同时，在较大的动应力比下，由于超孔隙水压力的不断累积，使得红黏土的强度和刚度大大降低，并产生了较大的不可恢复的残余变形。因此，图11(a)、图12(a)没有像图10(a)那样表现为一系列近似平行的曲线。

2.3 红黏土残余孔压影响因素分析

不排水时，为了排除固结围压对试样超孔隙水压力的影响，对超孔隙水压进行归一化研究，定义动孔压比U*=U/Pc=U/((σ1+2σ3)/3)，(U为超孔隙水压力，σ1为轴向应力，σ3为径向应力)。

2.3.1 动应力比的影响 图13为不同动应力比下试样动孔压比随循环振次的变化曲线。由图13可知，不同动应力比下饱和红黏土的动孔压比都随着循环次数的增加而增大，在较大的循环次数后出现转折并逐渐趋向稳定。在相同的循环次数下，动应力比越大，动孔压比就越大。

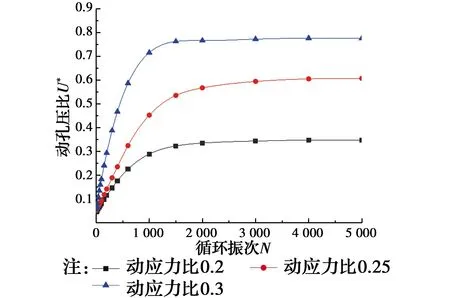
图13 动孔压比随循环振次的发展曲线(动应力比影响)Fig.13 Development curve of dynamic pore pressure ratio with cyclic vibration times (influence of dynamic stress ratio)

2.3.2 初始孔隙率的影响 图14为不同初始孔隙率试样的动孔压比随循环振次的发展曲线。不难发现，随着循环次数的增加，3组初始孔隙率试样的动孔压比差值逐渐增大；随着初始孔隙率的增大，动孔压比也逐渐增大，而且动孔压比达到稳定状态时所需要的循环次数逐渐增大。初始孔隙率为0.65的试样动孔压比达到稳定状态时所需要的循环次数为1 000次；初始孔隙率为0.7的试样动孔压比达到稳定状态时所需要的循环次数为2 000次；初始孔隙率为0.75的试样在循环次数为5 000次时动孔压比仍没有达到稳定状态。

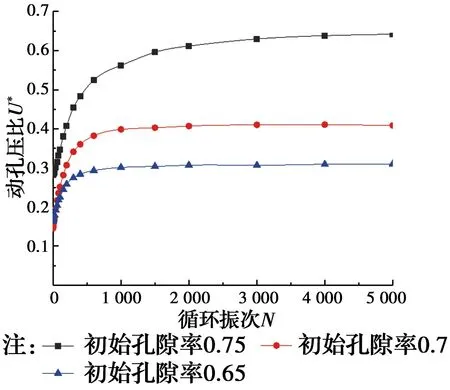
图14 动孔压比随循环振次的发展曲线(初始孔隙率影响)Fig.14 Development curve of dynamic pore pressure ratio with cyclic vibration times (influence of initial porosity)

2.3.3 固结围压的影响 图15为固结围压对试样动孔压比的影响曲线图。可以看出，随着循环次数的增加，不同固结围压下的试样动孔压比均表现为先急速增长后逐渐趋于平稳；在相同的循环次数下，固结围压越大，试样的动孔压比越大。

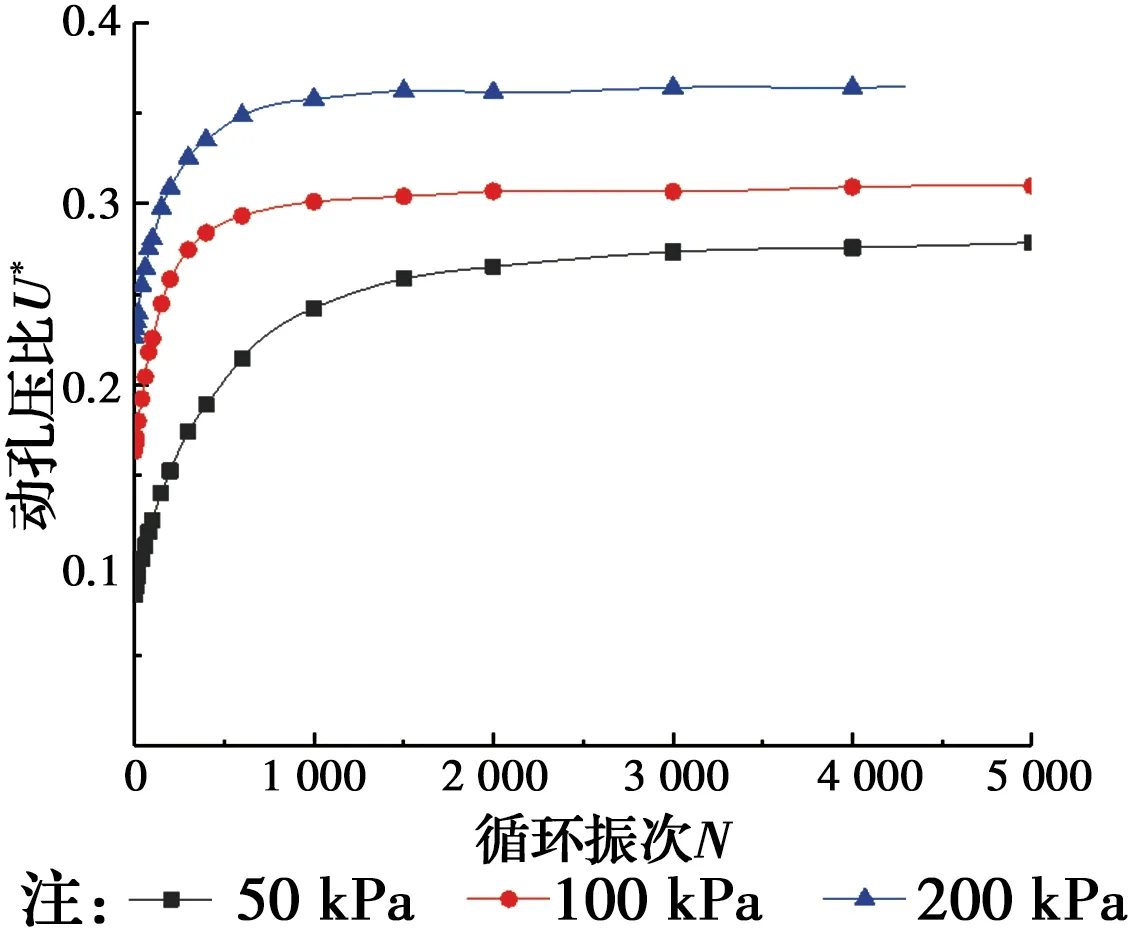
图15 动孔压比随循环振次的发展曲线(固结围压影响)Fig.15 Development curve of dynamic pore pressure ratio with cyclic vibration times (influence of consolidation confining pressure)

2.3.4 加载频率的影响 图16为加载频率对试样动孔压比的影响曲线图。从图16可以看出，加载频率对试样的残余孔压产生了很大的影响，随着循环次数的增加，不同加载频率下的孔压都是先快速增大，然后出现拐点，最终趋于稳定；加载频率越大，试样产生的残余孔压越小，孔压达到稳定时所需要的循环次数也越小。加载频率为0.5 Hz时，试样孔压达到稳定所需要的循环次数是2 000次，加载频率为1.0 Hz时，试样孔压达到稳定所需要的循环次数是1 500次，加载频率为2.0 Hz时，试样孔压达到稳定所需要的循环次数是1 000次。

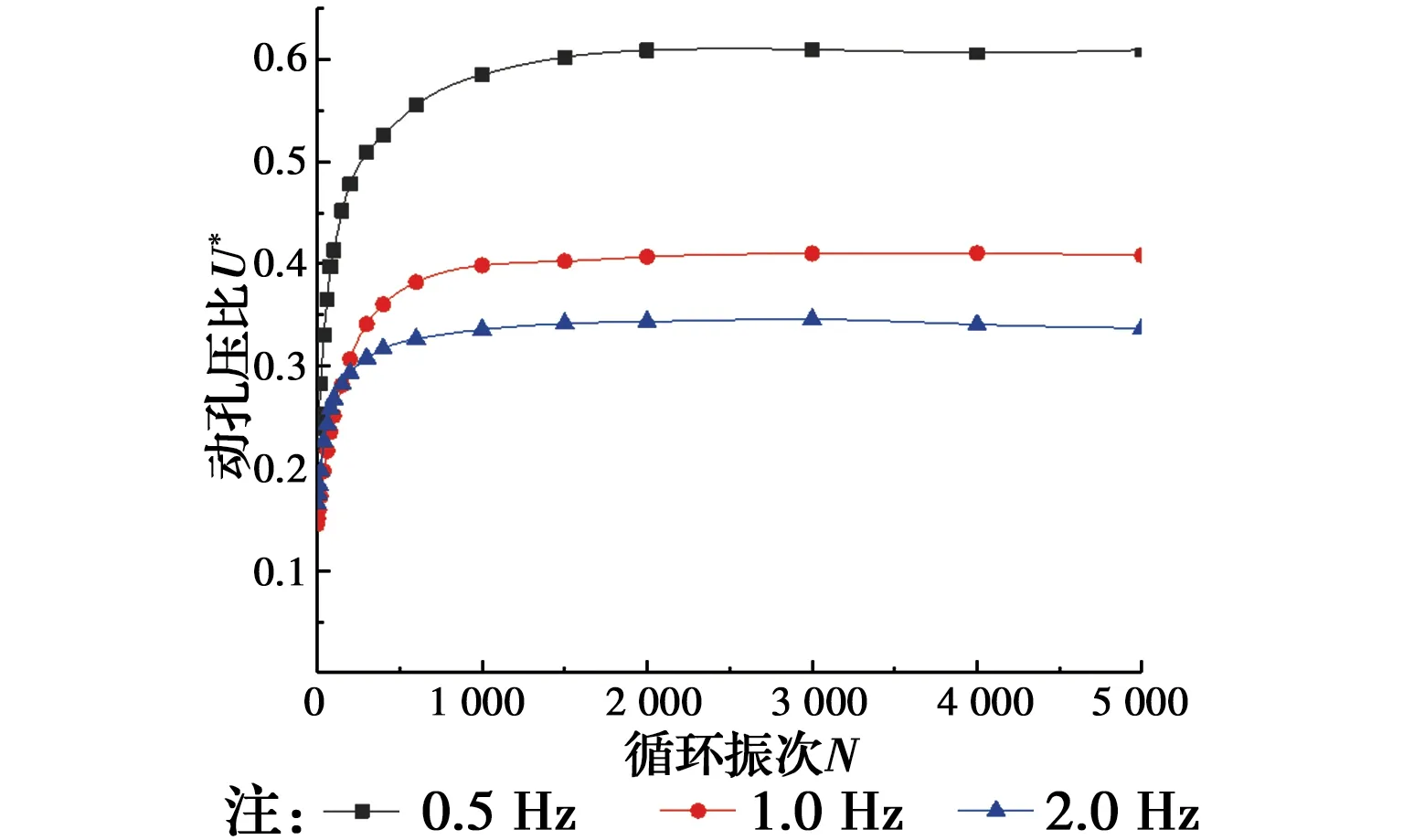
图16 动孔压比随循环振次的发展曲线(加载频率影响)Fig.16 Development curve of dynamic pore pressure ratio with cyclic vibration times (influence of loading frequency)

3 结论

通过对南昌地区饱和重塑红黏土的单向循环压缩动三轴试验研究，得出以下结论。

1)随着动应力比的增大，塑性累积应变也不断增大，试样由强化状态向破坏状态过渡；当动应力比小于临界动应力比时，塑性累积应变越大，应变发展曲线拐点的出现越滞后；在相同的动应力比下，试样初始孔隙率和固结围压越大，累积应变越大，加载频率越高，累积应变反而越小，同时，不排水条件下的累积应变要大于排水条件下的累积应变。

2)通过对土体应力-应变滞回曲线的分析，发现试验加载初期，滞回曲线分布较为稀疏，后期则较为密集；随着循环振次的增加，滞回圈略有拉长并偏向轴向应变一侧倾斜，单个循环周期内滞回圈的面积也有所增大，动应力比越大，这种变化越显著；随着动应力比的增大，土体的软化程度也越大，但在较高的循环振次下，软化程度减弱。

3)各影响因素下试样的动孔压随荷载循环次数的发展曲线的形态特征基本一样，均表现为起始快速增长，然后出现拐点，最终趋于稳定；试样的动孔压比随初始孔隙率、固结围压、动应力比的增大而增大，随加载频率的增大而减小；动孔压达到稳定时所需要的荷载循环次数，不同的影响因素下表现不一。

以上结论的得出是动应力比小于临界动应力比条件下的试验结果，对于动应力比大于或等于临界动应力比的情况，需另做研究。

依据试验结果建立不同影响因素下的红黏土塑性累积应变模型，由此可预估不同动荷载作用下红黏土路基的沉降量及达到稳定变形时所需要的年限，这是接下来要进行的研究工作。