高超声速滑翔飞行器倾侧角影响分析

孟繁卿，田康生

(1. 空军预警学院研究生大队， 武汉 430019； 2. 空军预警学院四系， 武汉 430019)

0 引 言

随着各国反导预警体系的构建与完善，传统弹道导弹的威胁有下降的趋势。临近空间高超声速飞行器的出现，使得针对弹道导弹构建的反导体系面临新的挑战[1]。临近空间高超声速飞行器，既具有弹道导弹高速、远距离打击的特点，又具有航空飞行器可灵活机动的特点。临近空间高超声速飞行器的独特优势使其逐渐成为各国研究的热点。

临近空间高超声速滑翔飞行器作为当前高超声速飞行器研究的重点，在飞行过程中依靠空气动力实现滑翔飞行，其飞行速度大于Ma5，飞行高度大于20 km。高超声速滑翔飞行器滑翔段的飞行控制参数主要是攻角和倾侧角[2]，所以飞行器滑翔段的弹道特性也主要受攻角和倾侧角影响。文献[3]在纵向平面内分析了平衡滑翔条件下，飞行器状态变量与状态变量、状态变量与过程变量之间的关系，分析了跳跃滑翔条件下，初始状态对弹道特性的影响。文献[4]利用平衡滑翔条件，构建了高超声速飞行器航程与飞行时间的解析式，定量分析了升阻比对滑翔射程的影响规律。文献[5]在最大升阻比平衡滑翔条件下，利用数值积分的方法求得了飞行速度、航程等状态变量的解析式，提出并证明了最大升阻比平衡滑翔是航程最优的弹道的观点。文献[6]从工程应用的角度分析了再入攻角优化问题的多种约束，得到了再入攻角的上下限及攻角设计空间，提出了再入攻角剖面的设计方案，所提方案在覆盖区优化问题上有较高的应用价值。文献[7]将热流密度、动压和过载等过程约束转化为攻角约束，将过程约束边界转化为攻角的上下限，减少了弹道规划中约束变量的个数，降低了弹道规划的复杂度和计算量。文献[8]针对高超声速飞行器受空气扰动后攻角易发生变化的问题，分析了攻角动态变化时对高超声速飞行器气动特性的影响，指出其性能参数的变化规律虽然没有显著改变，但存在迟滞现象。文献[9]对高超声速飞行器在大攻角情况下的气动特性进行了分析，指出大攻角时飞行器的气动参数呈现非线性的特点，飞行器的纵向静不稳定性随攻角增大而增大。文献[10]通过对高超声速飞行器的轨迹仿真得到了飞行器升阻比的变化规律，给出了升阻比的解析表达式，由升阻比解析式可知升阻比本质还是受飞行器攻角控制。

以上文献的研究成果丰富，为我们明晰高超声速飞行器的弹道特性、进行轨迹规划和优化提供了很好的借鉴。但不管是弹道特性分析还是弹道规划设计，多是集中在纵向平面，以攻角的设计、优化或攻角对飞行状态和过程约束的影响分析为主，而忽略了倾侧角对飞行器飞行速度、飞行高度和过程约束的影响[2]。为了将已有文献研究成果的适用范围进一步扩展，需要研究倾侧角对飞行器飞行速度、飞行高度和过程约束的影响。通过分析倾侧角对高超声速滑翔飞行器滑翔段飞行速度、飞行高度、过程约束的影响，可为弹道特性分析、弹道设计、弹道优化和轨迹预测等提供借鉴。

1 高超声速滑翔飞行器滑翔段运动方程

(1)

其中升力、阻力的计算可由式(2)求得。ρ是空气密度，S是飞行器的参考面积，CL是飞行器的升力系数，CD是飞行器的阻力系数[4,12]。

(2)

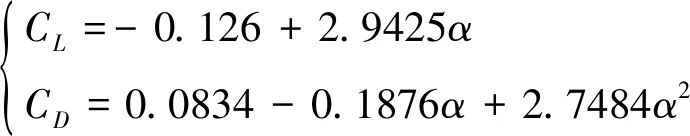
(3)

2 飞行弹道控制参数模型及飞行约束条件

2.1 飞行弹道及弹道控制参数模型

临近空间高超声速滑翔飞行器的典型弹道按照运动平面可分为：纵向平衡滑翔弹道、纵向跳跃滑翔弹道、横向无机动弹道、横向弱机动弹道、横向强机动弹道。

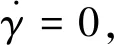
(4)

纵向跳跃滑翔弹道控制参数模型即攻角α的参数模型[13]，如式(5)所示。αmax为最大飞行攻角，α(L/D)max为最大升阻比攻角。V1和V2分别为攻角参数变化的两个临界速度。

α(V)=

(5)

临近空间高超声速滑翔飞行器横向机动的主要控制参数是倾侧角ε，如果横向无机动，则可令倾侧角为零，即ε=0°。

横向弱机动弹道轨迹平滑，倾侧角通常只翻转一次，飞行器横向只机动一次。横向弱机动弹道控制参数模型如式(6)所示。εd为初始倾侧角。A是飞行器飞行过程中在水平面上的投影点，O是飞行器初始位置在水平面上的投影点，F是目标点在水平面上的投影点，B是O和F连线上的一个参照点。

(6)

(7)

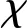
(8)

2.2 飞行约束条件

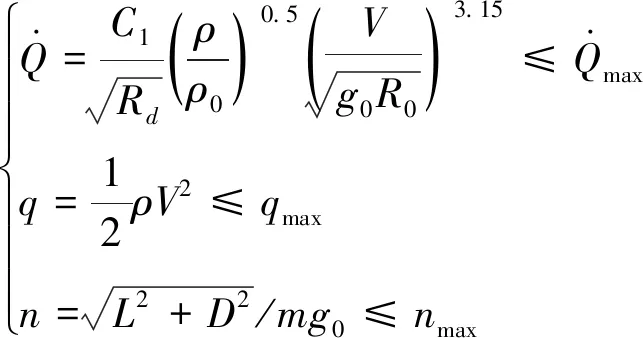
(9)

ρ(z)=ρ0ez/ξ

(10)

终端约束条件如式(11)所示，Ω是满足终端约束的空间位置集合，(xf,yf,zf)是滑翔段结束时刻飞行器的位置坐标，hf是终端高度约束，df是滑翔段结束时刻飞行器与目标点的距离约束。

Ω={(xf,yf,zf)||zf|≥hf,

((xf-xt)2+(yf-yt)2)1/2≤df}

(11)

3 平衡滑翔倾侧角影响分析

3.1 飞行速度和高度解析解

由平衡滑翔条件式(4)可得，

Lcosε=mg0cosγ

(12)

将式(2)代入式(12)可得，

(13)

所以可推导出飞行速度表达式为，

(14)

将式(10)代入式(14)可得，

(15)

将式(15)整理可得，

(16)

式(16)对z求微分可得，

(17)

将式(16)代入式(17)可得，

(18)

又因为，

(19)

将式(1)代入式(19)可得，

(20)

由式(18)和式(20)可得，

(21)

将式(2)、(13)代入式(21)可得，

(22)

由式(22)可得飞行速度-倾侧角解析式，

(23)

所以飞行速度是关于倾侧角ε的偶函数。为方便讨论，参考文献[15]中倾侧角的取值。

式(23)两边对倾侧角ε求微分可得，

(24)

文献[16]已经证明速度倾角为负的小量，所以在同一攻角、同一速度倾角条件下，倾侧角越大，所需飞行速度越大。

V(ε)为关于ε的单调递增函数，所以其反函数一定存在，且也为单调递增函数，如式(25)所示。参考文献[5]中的结论，以最大升阻比攻角平衡滑翔，参考文献[16]中最大升阻比的取值，CL/CD=2.98,Vmin为Ma5，所以γ∈[-1.4717°,0°)。

(25)

由式(14)和式(23)可得，

(26)

对式(26)进行整理可得，

(27)

由式(10)和式(27)可得，

(28)

对式(28)整理可得高度-倾侧角解析式，

(29)

式(29)两边对倾侧角ε求微分可得，

(30)

将式(29)代入式(30)可得，

(31)

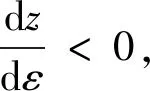
3.2 过程约束解析解

对式(9)中驻点热流密度计算公式整理可得：

(32)

将式(14)代入式(32)整理可得，

(33)

将式(27)代入式(33)可得热流密度-倾侧角解析式，

(34)

(35)

将式(34)代入式(35)可得，

(36)

对式(36)整理可得，

(37)

因为γ∈[-1.4717°,0°)，sinγ∈[-2.57×10-3,0)，所以将sin γ近似为零[16-17]，式(37)可化为，

(38)

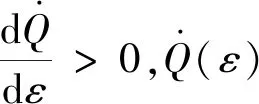
将式(2)、式(13)代入式(9)可得动压-倾侧角解析式，

(39)

式(39)两边对倾侧角ε求微分可得，

(40)

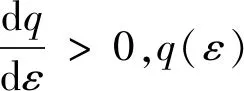
因为γ∈[-1.4717°,0°)，cosγ∈[0.9996,1)，所以cosγ≈1，式(39)可化为[16-17]，

(41)

将式(2)代入式(9)可得，

(42)

将式(13)代入式(42)整理可得过载-倾侧角关系式，

(43)

式(43)两边对倾侧角ε求微分可得，

(44)

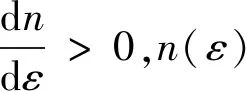
因为γ∈[-1.4717°,0°)，cosγ∈[0.9996,1)，所以cosγ≈1，式(43)可化为[16-17]，

(45)

所以由式(41)、式(45)可知，当倾侧角及攻角确定时，飞行器的动压和过载基本保持不变。

3.3 仿真校验

以洛克希德-马丁公司开发的高超声速通用气动飞行器CAV-H(Common Aero Vehicle)为例[18]。

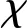
图1(a)为5个平衡滑翔弹道的三维弹道轨迹图，图1(b)为5个平衡滑翔弹道的横向平面弹道轨迹图。

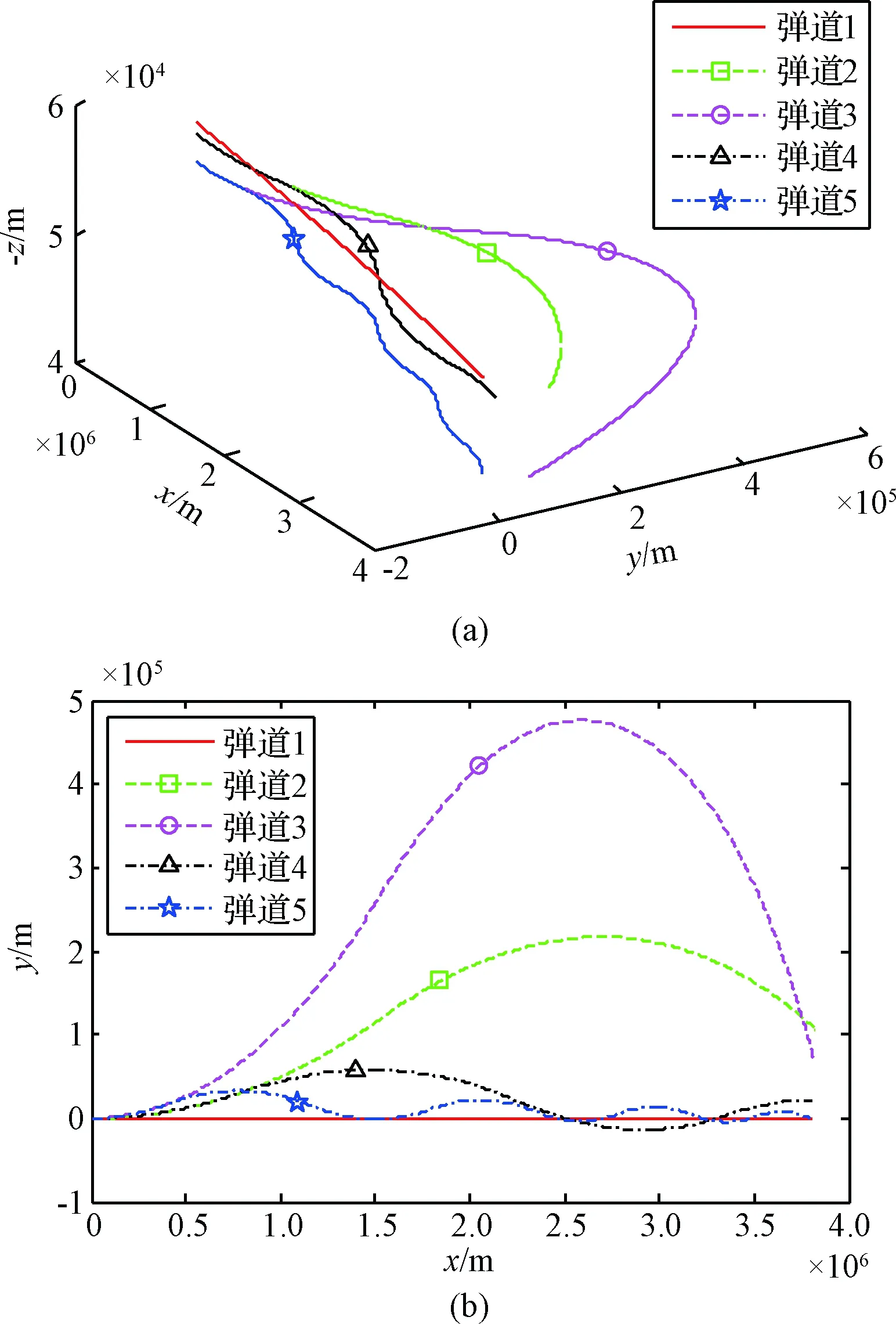
图1 平衡滑翔弹道轨迹仿真图Fig.1 Simulation diagram of equilibrium glide trajectory

3.3.1飞行速度和高度分析

表1是平衡滑翔各弹道速度解析解与数值解、高度解析解与数值解之间的最大绝对误差和最大相对误差表。从表1可以看出，5个弹道的速度解析解与数值解的最大绝对误差小于131 m/s、最大相对误差小于2%。5个弹道的高度解析解与数值解的最大绝对误差小于310 m、最大相对误差小于0.6%。由表1可知，平衡滑翔速度和高度的解析解具有较高的精度，能够作为飞行速度和高度的近似解。

图2是平衡滑翔各弹道的速度解析解与数值解、高度解析解与数值解的误差曲线图。从图2可以看出，随着飞行过程的进行，速度解析解与数值解的误差、高度解析解与数值解的误差都震荡收敛于0。飞行速度和高度的解析解作为一种近似解，围绕数值解上下波动，随着飞行过程的进行，解析解收敛于数值解。

表1 平衡滑翔速度和高度的解析解与数值解误差Table 1 The error between analytic solution and numerical solution of equilibrium glide speed and altitude

图3是平衡滑翔各弹道的速度和高度变化曲线图。对比弹道2和弹道3、弹道4和弹道5可知，在相同机动样式、不同倾侧角情况下，初始速度相同时，倾侧角越大，阻力越大，飞行速度下降越快，同一时刻相应弹道的飞行速度越小、高度越低。对比弹道2和弹道4、弹道3和弹道5可知，在相同倾侧角、不同机动样式情况下，初始速度相同时，飞行速度和高度的变化与机动样式无关。

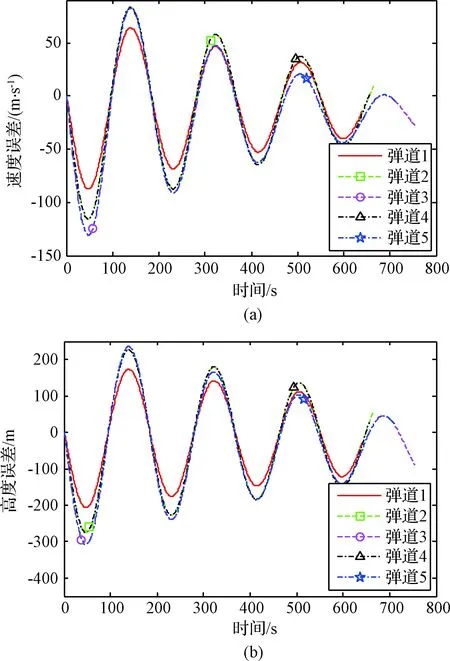
图2 平衡滑翔速度和高度误差曲线图Fig.2 Error curve of equilibrium glide speed and altitude

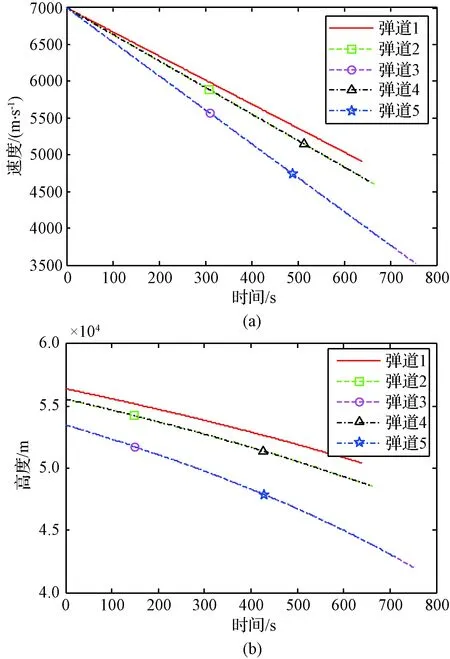
图3 平衡滑翔速度和高度变化曲线图Fig.3 Curve of speed and altitude of equilibrium glide

3.3.2过程约束分析

表2是平衡滑翔各弹道过程约束解析解与数值解之间的最大绝对误差和最大相对误差表。从表2可以看出，5个弹道的热流密度解析解与数值解的最大绝对误差小于40 kW/m2、最大相对误差小于5%。动压解析解与数值解的最大绝对误差小于280 Pa、最大相对误差小于0.6%。过载解析解与数值解的最大绝对误差小于8×10-3、最大相对误差小于0.6%。由表2可知，平衡滑翔弹道过程约束的解析解精度较高，能够用来估算飞行过程中过程约束的大小。

图4是平衡滑翔各弹道的过程约束解析解与数值解的误差曲线图。图4(a)是平衡滑翔各弹道的热流密度解析解与数值解的误差曲线图。从图4(a)可以看出，随着飞行过程的进行，热流密度解析解与数值解的误差震荡收敛于0，解析解作为一种近似解，围绕数值解上下波动，逐渐收敛于数值解。

图4(b)和图4(c)分别是平衡滑翔各弹道的动压解析解与数值解的误差曲线图、过载解析解与数值解的误差曲线图。从图4(b)和图4(c)可以看出，随着飞行过程的进行，动压解析解与数值解的误差、过载解析解与数值解的误差均呈现变大的趋势。因为动压和过载的解析解在计算过程中将cosγ近似为1，而实际飞行过程中速度倾角是缓慢变小的，所以动压和过载的解析解与数值解之间存在一定误差。但动压解析解与数值解的相对误差较小，小于0.6%；过载解析解与数值解的绝对误差较小，在10-3量级

表2 平衡滑翔过程约束的解析解与数值解误差Table 2 The error between analytic solution and numerical solution of equilibrium glide process constraints

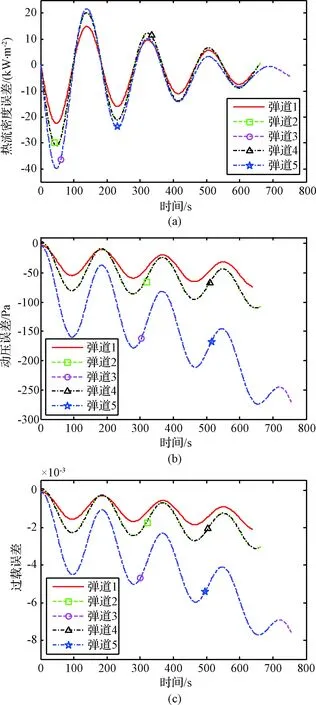
图4 平衡滑翔过程约束误差曲线图Fig.4 Error curve of equilibrium glide process constraints

。

图5是平衡滑翔各弹道的过程约束变化曲线图。图5(a)是热流密度变化曲线图，对比弹道2和弹道3、弹道4和弹道5可知，在相同机动样式、不同倾侧角情况下，初始速度相同时，倾侧角越大，阻力越大，飞行速度下降越快，相应弹道的热流密度下降越快。对比弹道2和弹道4、弹道3和弹道5可知，在相同倾侧角、不同机动样式情况下，热流密度的变化与机动样式无关。

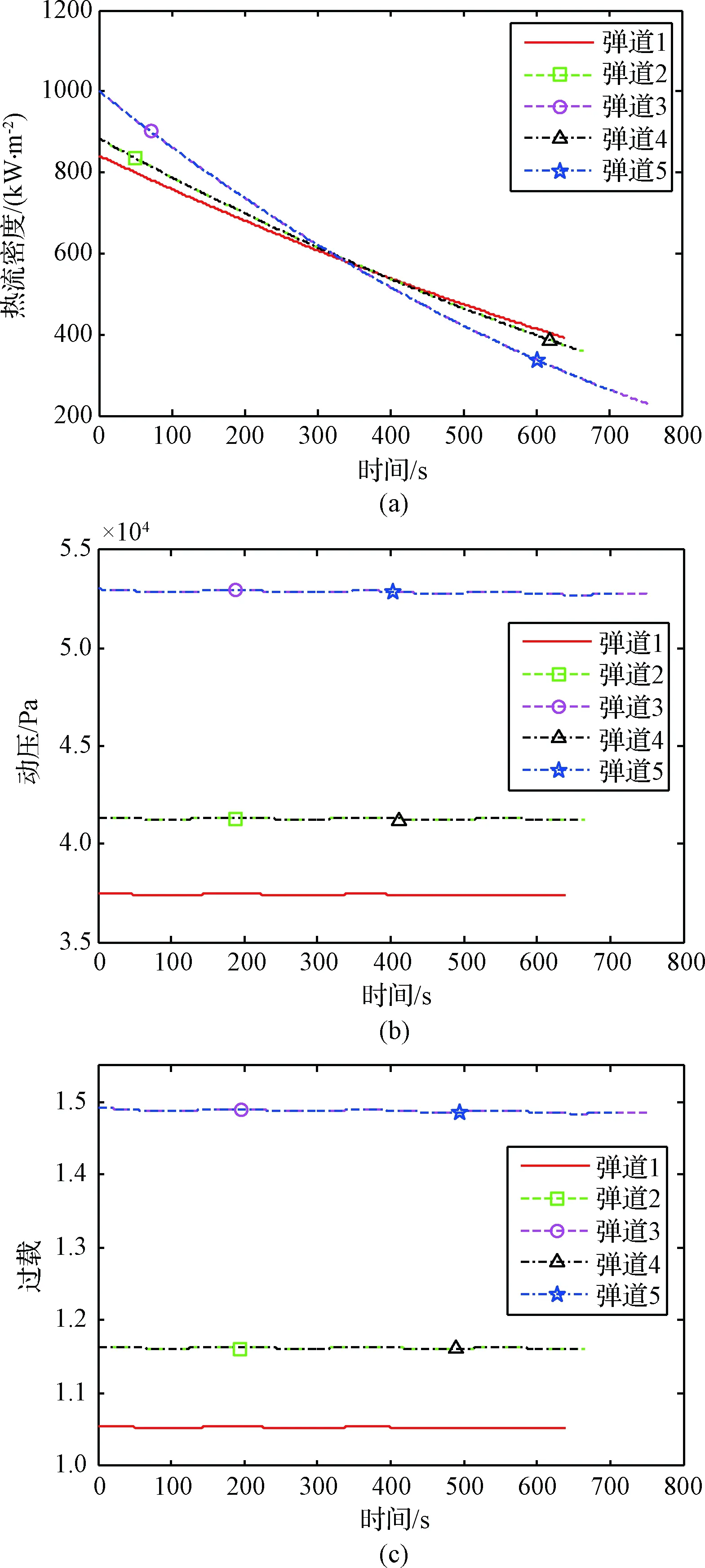
图5 平衡滑翔过程约束变化曲线图Fig.5 Curve of equilibrium glide process constraints

图5(b)和图5(c)是动压和过载变化曲线图。对比弹道2和弹道3、弹道4和弹道5可知，在相同机动样式、不同倾侧角情况下，初始速度相同时，倾侧角越大，为平衡重力，所需空气密度越大、飞行高度越低，相应弹道的动压、过载越大。对比弹道2和弹道4、弹道3和弹道5可知，在相同倾侧角、不同机动样式情况下，动压和过载的变化均与机动样式无关。

4 跳跃滑翔倾侧角影响分析

跳跃滑翔弹道不满足平衡滑翔条件，因此无法通过理论推导得出飞行速度、飞行高度、过程约束与倾侧角之间的解析式。以CAV-H为例，采用数值仿真的方法分析倾侧角对飞行速度、飞行高度、过程约束的影响。

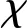
图6(a)为5个跳跃滑翔弹道的三维弹道轨迹图，图6(b)为5个跳跃滑翔弹道的横向平面弹道轨迹图。

图6 跳跃滑翔弹道轨迹仿真图Fig.6 Simulation diagram of skip glide trajectory

4.1 飞行速度和高度分析

跳跃滑翔弹道的飞行器速度、高度变化曲线如图7所示。由图7可知，弹道7和弹道9、弹道8和弹道10的速度、高度变化曲线基本重合，说明飞行速度、高度变化均与机动样式无关。对比弹道7和弹道8、弹道9和弹道10可知，在相同初始速度情况下，倾侧角越大，阻力越大，飞行速度下降越快，飞行高度波动变化幅度越小，同一时刻相应弹道的飞行速度越小、飞行高度越低。

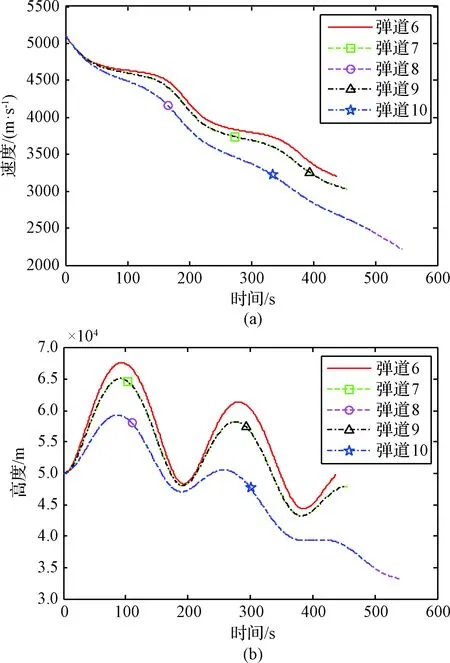
图7 跳跃滑翔速度和高度变化曲线图Fig.7 Curve of skip glide speed and altitude

4.2 过程约束分析

跳跃滑翔弹道过程约束变化曲线如图8所示。由图8可知，弹道7和弹道9、弹道8和弹道10的热流密度、动压、过载变化曲线基本重合，说明热流密度、动压和过载等过程约束的变化与机动样式无关。对比弹道7和弹道8、弹道9和弹道10的过程约束的变化曲线可知，在相同初始速度情况下，倾侧角越大，阻力越大，飞行高度波动变化幅度越小，飞行高度对应的空气密度波动变化幅度越小，相应弹道过程约束的波动变化幅度越小。

图8 跳跃滑翔过程约束变化曲线图Fig.8 Curve of skip glide process constraints

5 结 论

通过理论推导和数值仿真的方法分别对平衡滑翔和跳跃滑翔两种情况下，倾侧角对飞行速度、飞行高度、过程约束的影响进行了分析。

采用平衡滑翔弹道滑翔时，通过理论推导得出了飞行速度、飞行高度、过程约束与倾侧角之间的解析式。数值仿真结果表明,理论推导得出的解析解具有较高的精度，可用于数值解的近似计算。解析解作为一种近似解，可用来分析飞行速度、飞行高度和过程约束的变化规律。在平衡滑翔条件下，飞行速度、飞行高度和过程约束的变化均与机动样式无关。在相同初始速度情况下，倾侧角越大，相应弹道飞行速度、飞行高度、热流密度下降越快，动压和过载越大。

采用跳跃滑翔弹道滑翔时，飞行速度、飞行高度和过程约束的变化均与机动样式无关。在相同初始速度情况下，倾侧角越大，飞行速度下降越快，同一时刻相应弹道的飞行速度越小、飞行高度越低，飞行高度和过程约束的波动变化幅度越小。

不管是平衡滑翔还是跳跃滑翔，飞行速度、飞行高度和过程约束都与机动样式无关，而与倾侧角有关。机动样式主要对横向机动距离和弹道变轨有影响，而倾侧角对横向机动距离和弹道变轨影响如何则有待于进一步研究。