双层环形桁架可展天线机构运动特性与动力学分析
2020-05-20韩博许允斗姚建涛郑东李永杰赵永生
韩博, 许允斗,2, 姚建涛,2, 郑东, 李永杰, 赵永生,2
(1.燕山大学 河北省并联机器人与机电系统实验室, 河北 秦皇岛 066004;2.燕山大学 先进锻压成形技术与科学教育部重点实验室, 河北 秦皇岛 066004)
0 引言
随着空间通讯、军事侦察以及对地观测等各类航天任务的不断发展,宇航空间机构的尺寸越来越大[1]。由于运载火箭有效载荷舱空间有限,空间可展机构这类可以在发射和运载时收拢、入轨到位后展开的机构在卫星平台、空间站以及航天飞行器上得到了广泛应用,并逐渐成为航空航天领域的研究热点之一[2-5]。
空间可展机构在航空航天领域的一个重要应用是作为星载天线的展开与支撑机构[6]。网状反射面可展天线是星载天线中重要的一类,主要由可展开支撑机构和索网结构张拉形成的反射面构成,具有口径大、收拢率高以及质量轻的特点,在星载大口径天线领域得到广泛应用[7]。目前研制成功的大口径星载空间可展天线类型主要有构架式可展天线、环形桁架式可展天线、伸展肋式可展天线以及环柱形可展天线等[8-10]。
环形桁架式可展天线具有收拢率较高以及桁架质量较小的特点,相较于其他类型,随着天线口径的增大其质量并不呈比例增加,是空间大口径和超大口径天线较为理想的结构形式[11]。美国NGST公司在2000年研发的AstroMesh天线是环形桁架可展开天线在轨应用的成功范例,该天线从最初的2.5 m到现在运用较多的12.5 m口径,经历了7代产品升级,并先后在Inmarsat-4系列、Thuraya系列和MBSAT系列卫星上成功应用[12];由于单层环形桁架机构在口径较大时整体刚度较低,Escrig[13]最早于1985年提出了Pactruss双层环形桁架可展机构;You等[14]基于剪叉机构采用绳驱动研制了环形桁架机构样机;Datashvili等[15]研制成功了口径为6 m的双层环形可展开桁架机构。国内学者研制了单、双层环形桁架可展开天线与四面体构架式可展开天线的原理样机[16-18];也有学者分别构造了大型可展机构[19-20];史创等[21]提出了曲柄滑块式平面可展机构单元,并在此基础上设计了单、双层环形桁架可展机构并制作了原理样机。综上所述,相关科研人员在大口径星载环形桁架式可展天线领域做了较多研究,但是总体而言,目前在轨运行的环形桁架可展天线机构类型仍然较少。
在空间机构的运动特性与动力学分析方面,杨毅等[22]分析了一类多面体伸展臂机构;Chen等[23]、Shang等[24]和Chen等[25]研究了Bricard和Bennett连杆机构在构造空间可展机构时的运动特性;Zhao等[26]和李端玲等[27]利用螺旋理论,分别分析了平面型和球面型剪叉机构的运动特性;Wei等[28]基于螺旋理论和图论分析了魔术花球机构的自由度问题;Sun等[29-30]基于螺旋理论分别分析了剪叉机构组合单元的自由度、运动学以及动力学等问题;曲梦可等[31]研究了一种轮腿混合机器人的机械腿动力学建模问题。具体到空间可展开天线机构方面,许允斗等[32]基于螺旋理论,针对四面体构架式可展天线提出了一种拆杆等效的自由度分析方法;齐朝晖等[33]研究了周边桁架式可展开天线展开运动学与控制问题;Patel等[34]针对一种环状可展天线机构,建立了整体机构的运动学和动力学模型,并研究了摩擦对其展开运动的影响;刘瑞伟等[35]分析了一种大口径索肋张拉式折展天线的动力学特性问题;李团结等[36]研究了周边桁架可展天线的展开过程动力学问题;彭云等[37]研究了重力对大型环形可展天线展开动力学的影响。以上文献针对不同类型的空间机构及可展开天线机构进行了研究,但由于双层环形桁架可展天线机构属于复杂的空间多环耦合机构,杆件与运动副数量较多,自由度及运动学与动力学分析较为困难,目前多采用软件仿真模拟,难度较大且普适性较低。整体而言,从理论上针对此类机构进行相关分析的研究较少。
本文提出一种双层环形桁架可展天线机构,分析了双层环形桁架机构的构型机理并进行机构分解;基于螺旋理论分析了机构的自由度,并分析了整体机构中各个构件的速度和加速度;基于牛顿- 欧拉方程和虚功原理,建立了整体双层环形桁架可展机构的动力学方程,最后进行了数值仿真验证。本文研究旨在丰富大口径环形桁架可展天线机构的构型,并为此类可展机构的运动特性和动力学分析提供参考。
1 双层环形桁架可展天线机构
双层环形桁架可展天线机构如图1所示,其整体为由连杆铰接而成的中心对称桁架机构,主要包括内层环形桁架、外层环形桁架和多个内外层桁架连接单元,其内层环形桁架和外层环形桁架均呈环状,且各有上下两个环状桁架机构,内外层桁架连接单元为剪叉机构单元,整体机构通过位于节点处的花盘连接件连接。
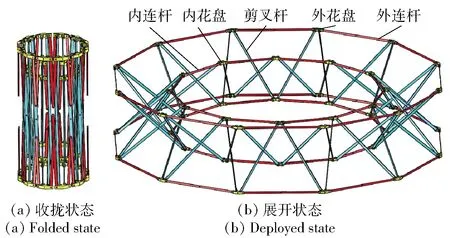
图1 双层环形桁架可展天线机构Fig.1 Double-ring truss deployable mechanism
图1(a)和图1(b)分别为双层环形桁架可展天线机构的完全收拢状态和完全展开状态,是其收藏运输和在轨工作时的位形状态。在整个机构的展开或收拢运动过程中其将处于半展开状态(见图2(a)),也是它的一般位形状态。半展开的内层环形桁架机构和外层环形桁架机构的结构相同,均由平面3R机构(R代表转动副)通过花盘连接件连接组成,内外层环形桁架通过中间的剪叉机构单元连接,整体机构中所含运动副均为转动副。对双层环形桁架可展机构进行结构分解,可以将其分解为一个闭环可展机构单元、多个非闭环可展机构单元以及两个平面3R机构,如图2(b)所示。

图2 双层环形桁架可展机构半展开状态及其结构分解Fig.2 Semi-deployed state of double-ring truss mechanism and its structural decomposition
2 双层环形桁架可展机构自由度分析
2.1 闭环可展机构单元自由度分析
针对闭环可展机构单元建立空间笛卡尔坐标系,如图3所示,坐标系原点O位于底部花盘连接件中心位置处,X轴由底部原点处的花盘连接件指向另一个花盘连接件,Z轴竖直向上,Y轴由右手定则确定。图3中:大写字母A~F表示各花盘连接件编号,l为剪叉杆上与内层花盘连接件相连的一段长度,L为与外层花盘连接件相连的一段长度,q为外层花盘连接件之间连接的两个连杆长度q;α为剪叉杆在OXY平面上的投影与Y轴的夹角,θ为相连两个剪叉杆之间的夹角,β为外层花盘之间连接的连杆与X轴的夹角。

图3 闭环可展机构单元及坐标系Fig.3 Closed loop deployable mechanism unit and coordinate system
设定内层花盘连接件上各转动副轴线与中心的距离为m,外层花盘连接件上各转动副轴线与中心的距离为n,在图3中各参数之间关系为
(1)
图3中,杆件编号用两两连接的花盘连接件编号表示,如花盘A和花盘E之间的剪叉杆编号为AE,花盘C和花盘D之间连接的两个连杆编号分别为CD1和CD2, 其他构件命名规则相同。基于图论和螺旋理论,用圆圈表示构件,用线条表示运动副,用带数字的运动旋量表示不同关节处的运动,如用$2表示连接杆件AE和DF转动副的运动,可以得到闭环可展开机构单元的旋量约束拓扑图,如图4所示。
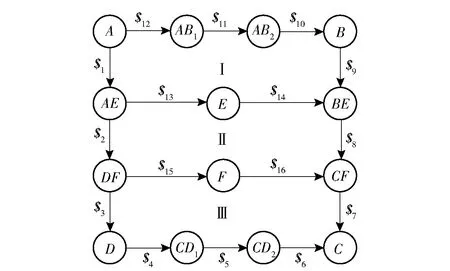
图4 闭环可展开机构单元旋量约束拓扑图Fig.4 Screw constraint topology of closed loop deployable mechanism unit
由连接杆件AB1和杆件AB2的转动副11空间位置坐标,可得
(2)
式中:r11表示转动副11的空间位置;n为花盘尺寸。
转动副11的转轴所在轴线方向矢量为
(3)
根据螺旋理论,可以得到转动副11的运动螺旋,其单位螺旋表达式为
(4)
同理可以得到图4中所示其他运动螺旋的表达式。用ω表示相应转动副的角速度,针对图4中的Ⅰ~Ⅲ 3个闭环,建立相应的旋量约束方程,可得闭环可展机构单元对应的旋量约束方程组为
(5)
式中:ωi为机构单元中转动副i的角速度量;0是六维零向量。
将(5)式写成矩阵的形式:
MN=0,
(6)
式中:
(7)
(8)
(9)
旋量约束矩阵M是一个18×16维矩阵,闭环可展开机构单元的自由度数对应于旋量约束矩阵的零空间维数,通过数值计算软件MATLAB计算,可得
rank(M)=15.
(10)
旋量约束矩阵M的列数为16,其零空间的维数为列数减去秩,因此可以得到闭环可展开机构单元的自由度数为1.
2.2 单元组合机构及双层环形桁架机构自由度分析
双层环形桁架可展机构可以分解为一个闭环可展机构单元、多个非闭环可展机构单元以及两个平面3R机构。由图2可以看出,非闭环可展机构单元包含构型相同的两种类型,区别仅为构件尺寸不同,由于构件尺寸不影响机构自由度,故在分析整体自由度时,可以对非闭环可展机构单元做统一处理。在图3所示的闭环可展机构单元基础上进行机构组合,组合一个非闭环可展机构单元,如图5所示。
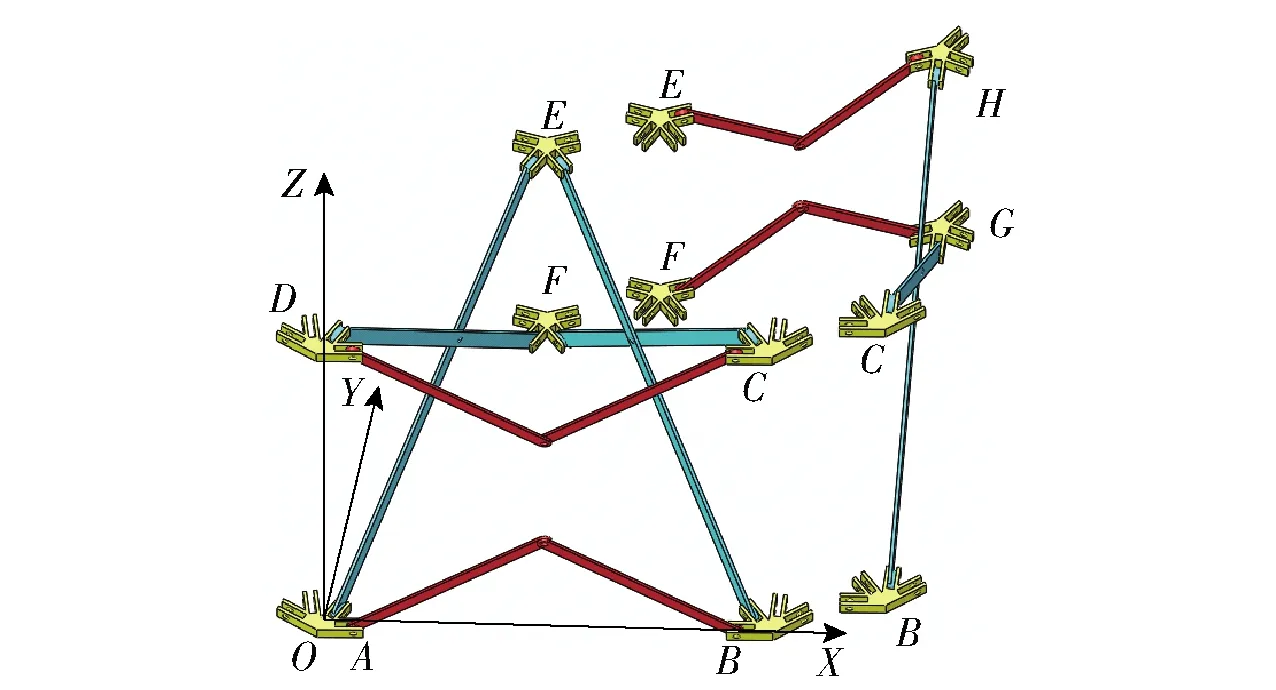
图5 单元组合机构及坐标系Fig.5 Unit combination mechanism and coordinate system
图5中,左侧的闭环可展机构单元与坐标系即为图3中的机构单元及坐标系,同样用大写字母对右侧机构单元的花盘连接件进行编号,杆件及运动副的编号规则同2.1节,可以得到图5中非闭环可展机构单元的旋量约束拓扑图,如图6所示。

图6 非闭环可展机构单元旋量约束拓扑图Fig.6 Screw constraint topology of non-closed loop deployable mechanism unit
针对图6中的ⅰ~ⅲ 3个闭环,建立相应的旋量约束方程,可得旋量约束方程组为
(11)
联立(5)式和(11)式,可得单元组合机构的旋量约束方程组为
(12)
(12)式写成矩阵的形式:
PQ=0,
(13)
式中:
(14)
系数矩阵P可以容易地通过(12)式得到。
图5中,花盘连接件B、C、E、F所连接的剪叉机构及其上所连接的5个转动副为两个机构单元所共用,联立(5)式和(11)式时,重复计算了两个机构单元共用的剪叉机构及转动副,因此在计算单元组合机构的自由度时,应除去重复计算的运动螺旋,即将$7、$8、$9、$14和$16分别去掉一个,只计算一次。这里将非闭环可展机构单元中重复计算的运动螺旋去掉,即图6中的红色虚线部分,因此(13)式中的系数矩阵P可以写为
(15)
式中:
(16)
(17)
由(15)式可得
rank(P)=rank(M)+rank(M′),
(18)
代入机构参数,可得

(19)
则单元组合机构的自由度为
d=u-rank(P)=27-26=1,
(20)
式中:d为自由度数;u为矩阵的列数。
由于矩阵M′为列满秩矩阵,(20)式也可以写为
d=uM+uM′-rank(M)-rank(M′)= [uM-rank(M)]+[uM′-rank(M′)]=uM-rank(M),
(21)
式中:uM为矩阵M的列数;uM′为矩阵M′的列数。
由(21)式可以看出,单元组合机构的自由度数仍然取决于矩阵M,单元组合机构的自由度数与单个闭环可展机构单元的自由度数相同。
由以上分析可知,当在单元组合机构的基础上继续添加非闭环可展机构单元时,整体机构的自由度仍然与单个闭环可展机构单元相同。同理可以分析得到,当在单个闭环可展机构单元上添加多个非闭环可展机构单元以及两个平面3R机构形成双层环形桁架可展机构时,其整体自由度仍然与单个闭环可展机构单元相同,双层环形桁架可展机构整体只具有一个自由度。由于机构中运动构件的运动自由度数小于或等于整体机构的自由度数[38],双层环形桁架可展机构中的各个运动构件也只有一个运动自由度。
3 双层环形桁架机构速度分析
在进行速度分析时,以图5所示的单元组合机构为基础,对双层环形桁架可展机构进行单元划分,将双层环形桁架可展机构划分为多个相同的单元组合机构,相邻单元组合机构之间共用4个花盘连接件以及一个剪叉机构,如图7所示。

图7 多个单元组合机构Fig.7 Multi-unit combination mechanism
3.1 单元组合机构速度分析
由2.2节分析可知,单元组合机构为单自由度机构,因此,若给定其中的一个输入,如ω1,通过(12)式中的旋量约束方程组可以解得各个角速度未知量,进而基于单元组合机构的构型关系以及图4和图6所示的旋量约束拓扑图,通过旋量运算便可以得到各个构件的旋量速度。
在图4所示的旋量约束拓扑图中,闭环Ⅰ中各个构件的旋量速度为
(22)
式中:VA、VAE、VAB1、VE、VAB2、VB、VBE分别为构件A、AE、AB1、E、AB2、B、BE的旋量速度。
在图4所示的旋量约束拓扑图的闭环Ⅱ中,构件AE、E和BE的旋量速度可以通过(22)式求出,闭环Ⅱ中其他构件的旋量速度可以由已经求得的构件旋量速度计算得到,以构件AE的旋量速度为基础,闭环Ⅱ中其他构件的旋量速度为
(23)
式中:VDF、VF、VCF分别为构件DF、F、CF的旋量速度。
同理,图4中的闭环Ⅲ以及图6中的闭环ⅰ~ⅲ中各个构件的旋量速度也可以依次求解出。
根据速度旋量的物理意义,各个构件i的角速度坐标量可以表示为
ωi=ω(Vi),
(24)
式中:ω(·)为取速度旋量的原部,即前3项。
速度旋量中包括构件的角速度和线速度,其原部为构件的角速度,对偶部为构件上原点重合点的线速度,因此构件的质心线速度可以表示为
vi=ν(Vi)+ω(Vi)×ri,
(25)
式中:ν(·)表示取速度旋量的对偶部,即后3项;ri表示坐标原点到构件质心位置的矢量。
通过以上分析计算,就可以完成整个单元组合机构的角速度和质心处线速度的求解。
3.2 其他单元组合机构速度分析
由于双层环形桁架可展机构为完全中心对称机构,各个单元组合机构尺寸完全相同,且关于环形桁架中心对称,若在各个单元组合机构处建立自身坐标系,则各个单元组合机构中位置相同的构件在自身坐标系下速度相同。
如图8所示,3.1节中单元组合机构中各个构件的速度是在图8中左侧所示的坐标系OXYZ中求得的。在与其相邻连接的右侧单元组合机构处建立坐标系O1X1Y1Z1,以花盘连接件B和K为例,花盘连接件B在坐标系OXYZ中的速度与花盘连接件K在坐标系O1X1Y1Z1中的速度相同,即
(26)
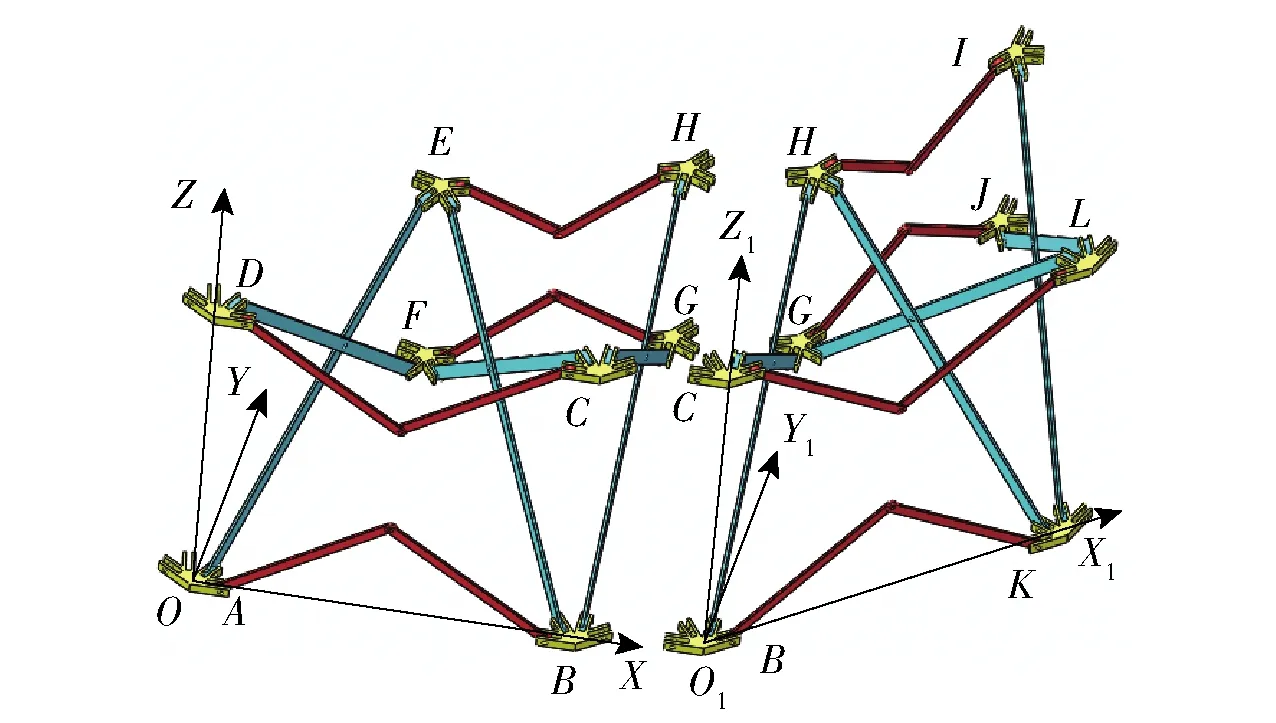
图8 两个单元组合机构及其坐标系Fig.8 Two-unit combination mechanisms and coordinate systems
图8中右侧的单元组合机构中其他构件也有类似关系,同理可以推广到整个双层环形桁架中其他单元和机构中。若整个双层环形桁架可以分为N个单元组合机构,则可建立OXYZ~ON-1XN-1YN-1ZN-1共N个坐标系,选定坐标系OXYZ为全局坐标系,相邻单元中所建坐标系X轴间夹角为δ=360/N,如图9所示。
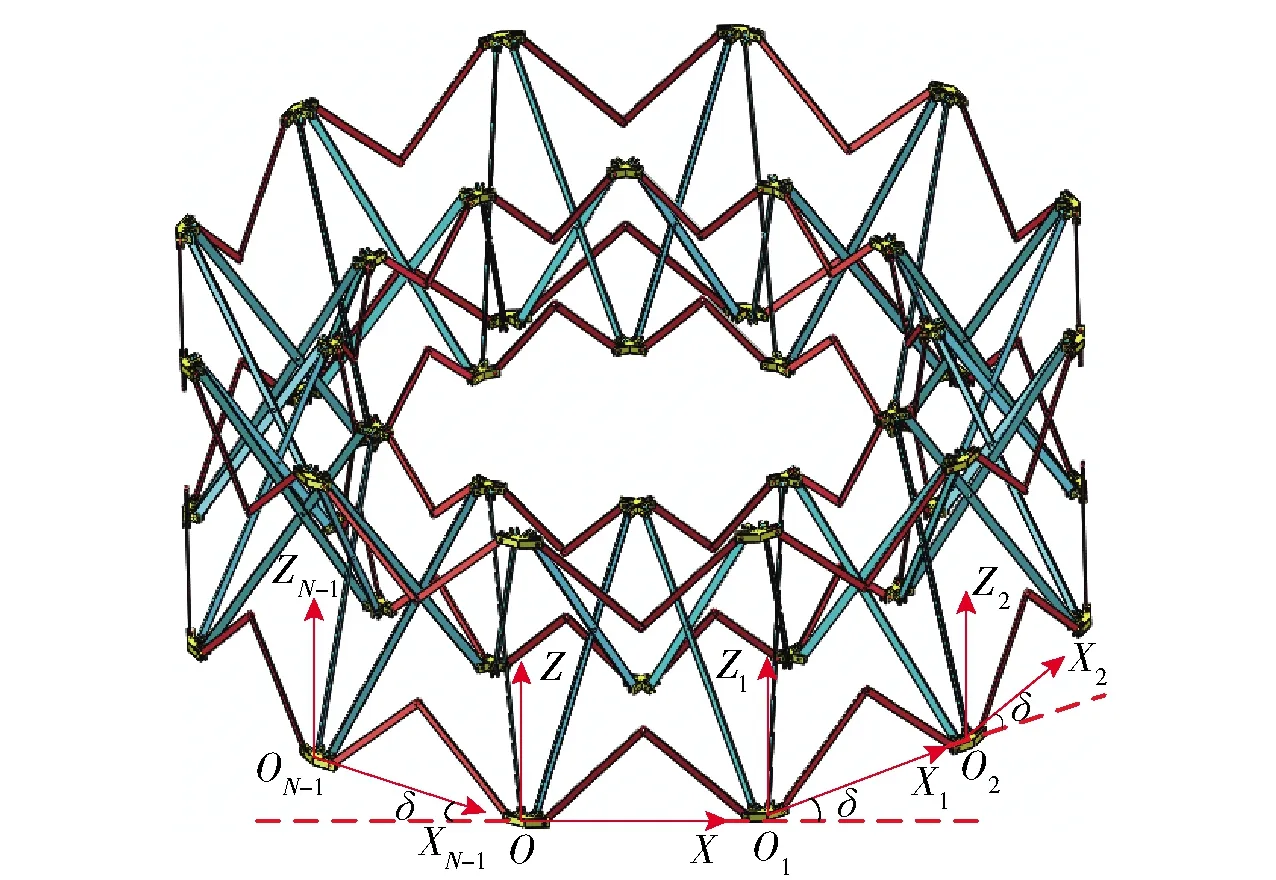
图9 双层环形桁架可展机构及坐标系Fig.9 Double-ring truss deployable mechanism and coordinate systems
选定坐标系OXYZ为全局坐标系,将各个构件速度表示在全局坐标系中,则有
(27)
式中:j为坐标系编号;
(28)
通过以上分析计算,就可以完成整个双层环形桁架可展机构中各个构件角速度和质心处线速度的求解,并将其表示在全局坐标系下。
3.3 雅可比矩阵
在求出各个构件的角速度和质心线速度之后,将其组合便可以得到构件的六维速度矢量,由于该机构为单自由度机构,只需要一个驱动,在各个构件六维速度矢量中通过符号运算提取出输入角速度,便可以得到该构件的雅可比矩阵:
(29)
式中:V′i为构件i的六维速度矢量;Ji(γ)为第i个构件的速度雅克比矩阵;γ为整体机构的驱动输入,即驱动角函数。
4 双层环形桁架机构加速度分析
旋量加速度公式[39]为
(30)
式中:Ai为机构中构件i的旋量加速度,表示构件上参考坐标系原点重合点的六维加速度量;εi为构件上参考坐标系原点重合点的角加速度量;a为构件质心处的线加速度;ω为构件的角速度;v为构件的质心线速度。由(30)式可以看出,六维旋量加速度中,前3项为构件的角速度,后3项为构件的线加速度减去其向心加速度量。
多刚体系统旋量加速度合成法则为
(31)
式中:Lie[]为李括号运算,结果为一个六维矢量。
若有两个旋量:
(32)
则两个旋量的李括号运算法则为
(33)
结合图4以及(31)式,可以得到各个闭环的旋量加速度方程,如由图4中的闭环Ⅰ可得
(34)
式中:AεBE表示构件BE相对于构件A的角加速度;εi为构件上参考坐标系原点重合点的角加速度;
(35)
因此有
(36)
同理在图4中的闭环Ⅱ、Ⅲ以及图6中的闭环ⅰ~ⅲ中也可得到相应的旋量加速度方程,在已知输入的角加速度(如ε1)情况下,通过求解(36)式及其他旋量加速度方程,便可以求解出单元组合机构中各个构件的旋量加速度。
在求出各个构件的旋量加速度后,提取其原部,可以得到各个构件的角加速度:
εi=ε(εi$i),
(37)
式中:ε(·)表示提取旋量加速度的原部,即前3项。
求解出各个构件的角加速度之后,即可对构件质心处的线加速度求解,各构件线加速度为
ai=[a(εi$i)+ωi×vi]+[ε(εi$i)×ri]+ [ωi×(ωi×ri)],
(38)
式中:a(·)表示提取旋量加速度的对偶部,即后3项。
同第3节中的速度分析,各个单元组合机构中位置相同的构件在自身坐标系下加速度相同,将各个单元组合机构中构件的加速度表示在全局坐标系中:
(39)
式中:Ok-1εOk为坐标系OkXkYkZk相对于坐标系Ok-1Xk-1Yk-1Zk-1的角加速度;Ok-1aOk为坐标系OkXkYkZk相对于坐标系Ok-1Xk-1Vk-1Zk-1的原点线加速度。
通过以上分析计算,就可以完成整个双层环形桁架可展机构中各个构件角加速度和质心线速度的求解,并将其表示在全局坐标系下。
5 动力学分析与验证
5.1 动力学建模
根据牛顿- 欧拉公式,构件所受的外力和力矩与其加速度和角加速度的关系为
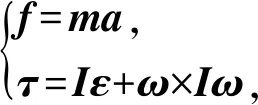
(40)
式中:f为构件所受外力;τ为构件所受力矩;I为构件的惯性张量。
在双层环形桁架可展机构中,各个构件的惯性力为
fi=-miai.
(41)
各个构件的惯性力矩为
(42)
对于自身坐标系与全局坐标系重合的单元组合机构中的各个构件,其惯性力和惯性力矩可以用(41)式和(42)式中的公式来计算。对于其他机构单元中的构件,其惯性力可以用(41)式来计算,但是其惯性力矩计算时需要增加一个旋转变换矩阵:
(43)
由于可展开天线服役环境为在轨空间环境,不用考虑重力的影响,将各个构件的惯性力和惯性力矩写成六维力矢量的形式:
(44)
由虚功原理,可得双层环形桁架可展开天线机构整体动力学方程为
(45)
式中:T为输入转矩;Ji为构件的雅可比矩阵。
5.2 机构可展性与动力学数值仿真验证
为验证前述理论分析的正确性,加工制作缩比模型样机,用于验证整体机构的可展性,模型样机展开过程如图10所示。

图10 样机展开过程Fig.10 Deployment process of prototype
建立双层环形桁架可展开天线机构的仿真模型,采用动力学仿真软件Adams和MATLAB软件进行数值计算与仿真模拟验证,仿真模型及参数如图11和表1所示。
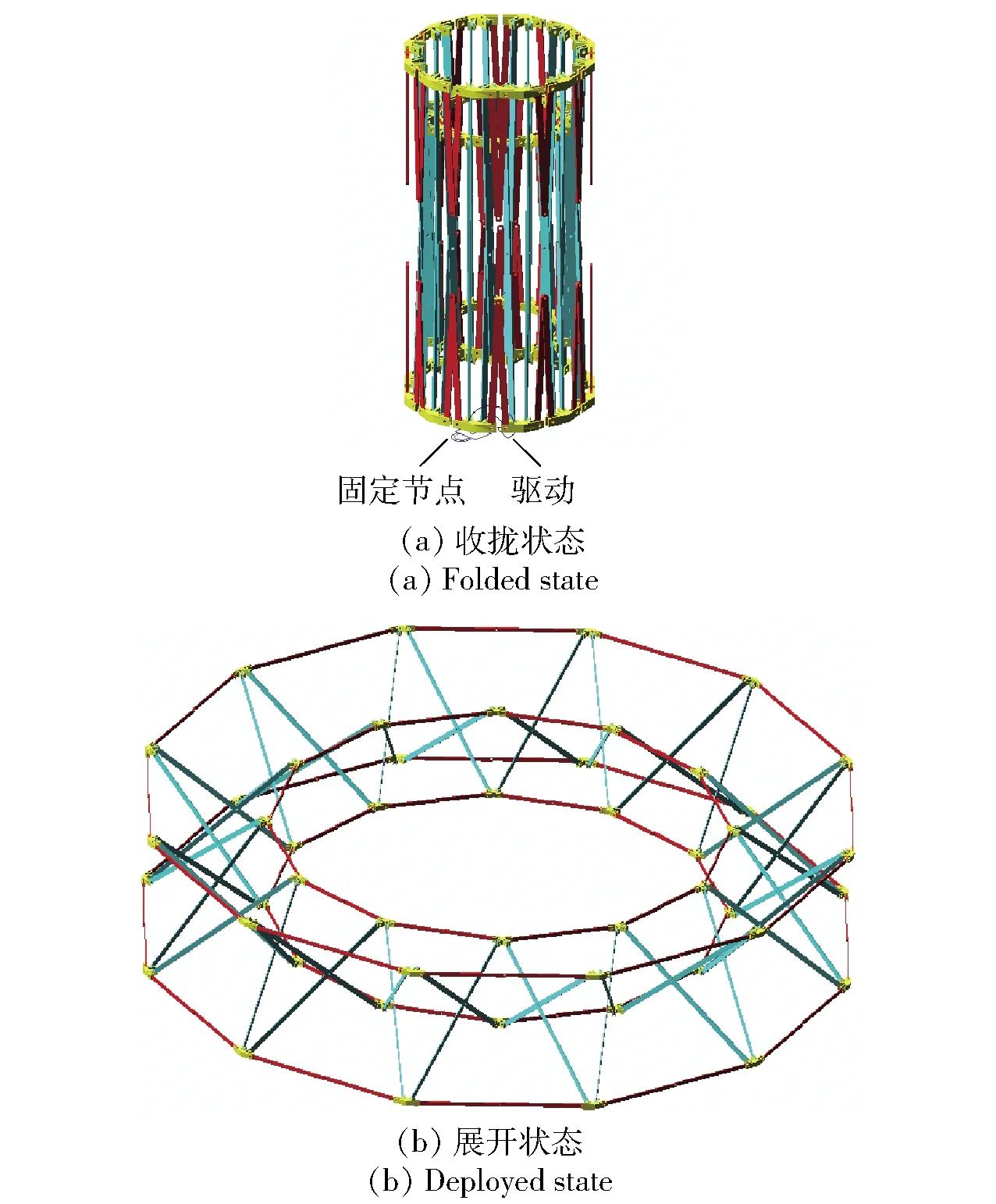
图11 仿真模型Fig.11 Simulation model
选取自身坐标系与全局坐标系重合的单元组合机构中的外层花盘连接件、外层环状连杆、剪叉杆、内层花盘连接件以及内层环状连杆为目标构件,理论计算结果和仿真结果如图12~图16所示。
通过图12~图16中的各个曲线,可以得出前面理论分析推导的正确性。从图12和图14中可以看出,在整个双层环形桁架可展机构的运动过程中,内层和外层花盘连接件的角速度和角加速度均为0,各个花盘连接件只有移动运动并无转动运动,即各个花盘连接件只有一个移动自由度,无转动自由度,这也跟前面分析得到的机构中各个运动构件只有一个自由度相对应。
6 结论
本文提出了一种双层环形桁架式可展天线机构,对其进行了结构分解和自由度分析。得出以下主要结论:

表1 结构及物理参数表Tab.1 Structural and physical parameters
注:t为仿真时间。
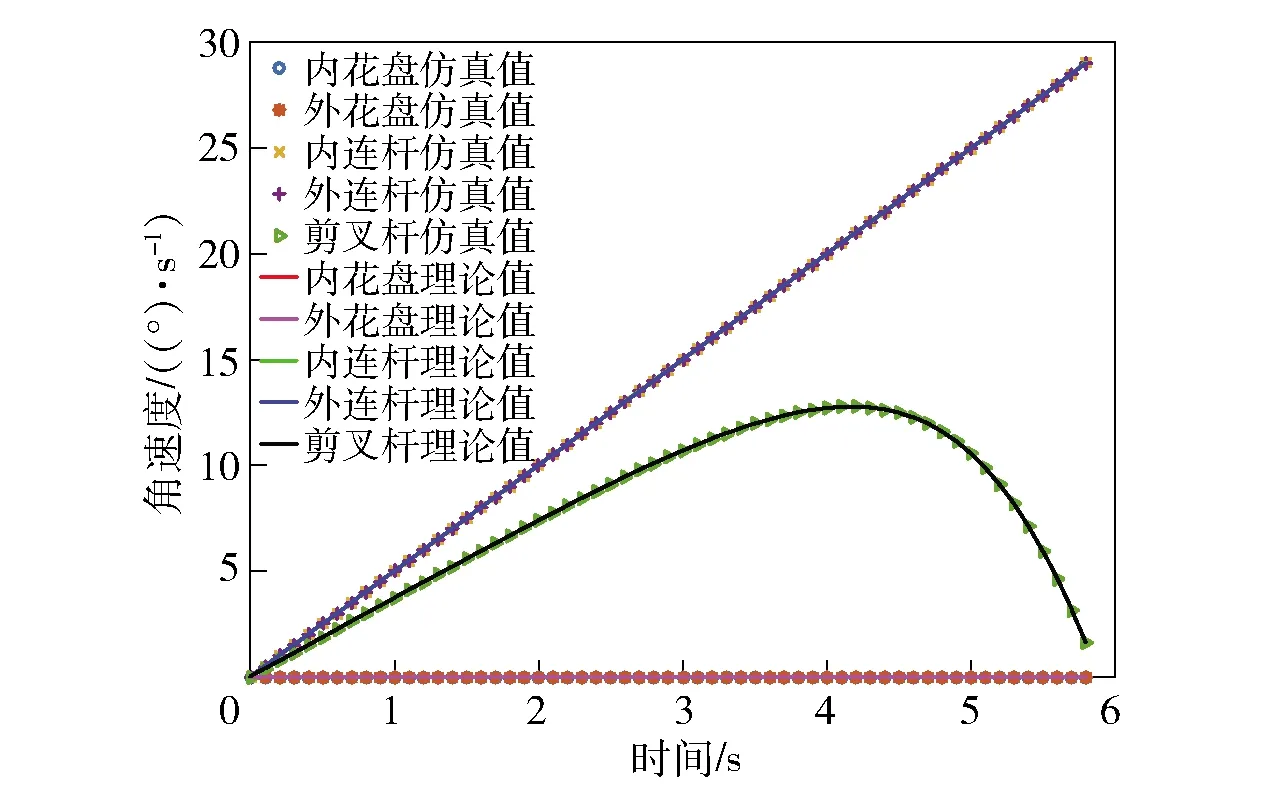
图12 各构件的角速度Fig.12 Angular velocities of components
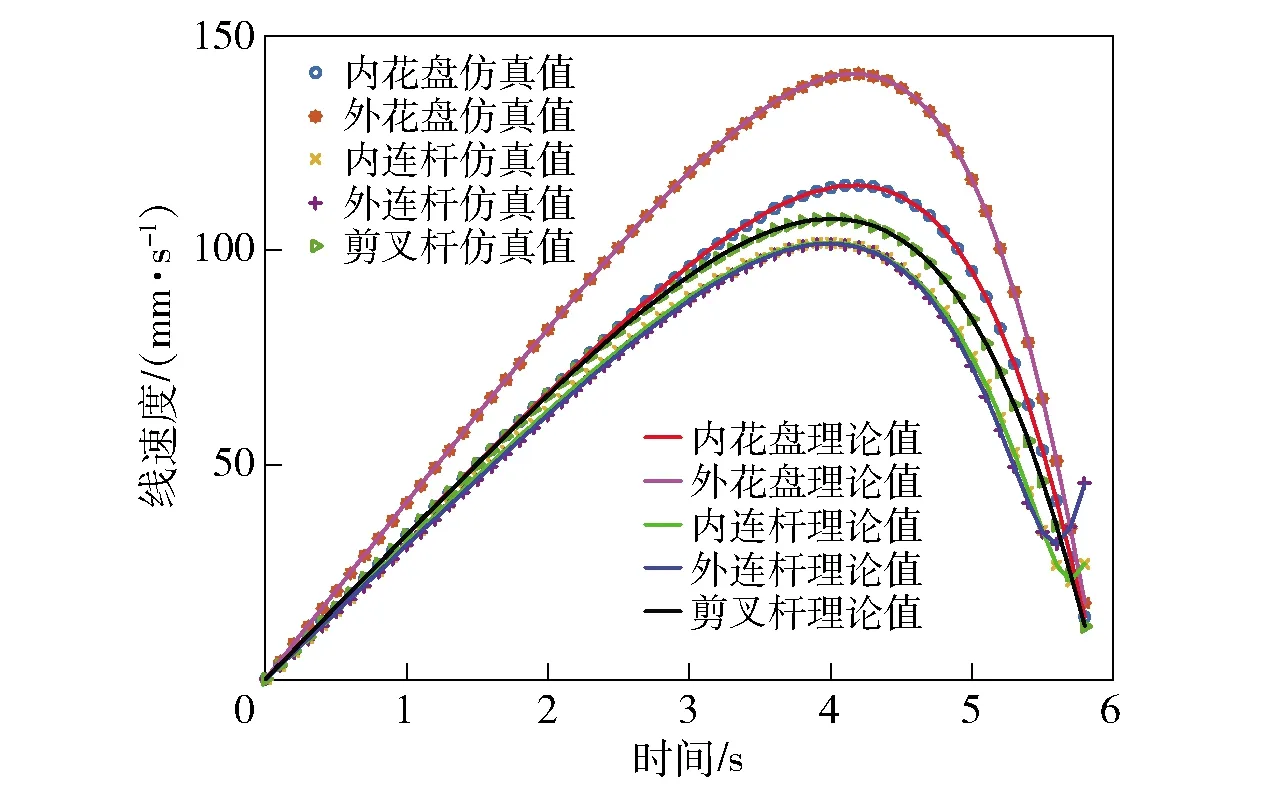
图13 各构件的质心线速度Fig.13 Centroid linear velocities of components

图14 各构件的角加速度Fig.14 Angular accelerations of components
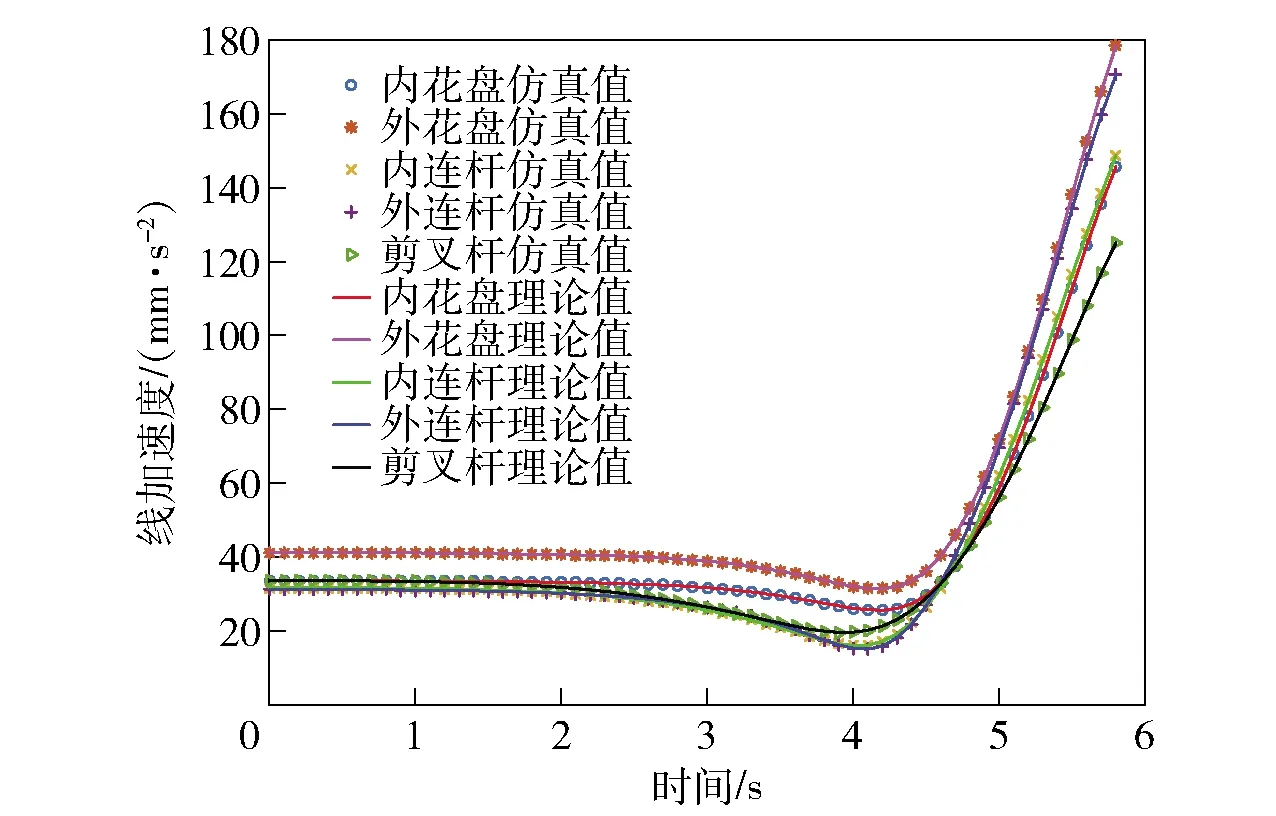
图15 各构件的质心线加速度Fig.15 Centroid linear accelerations of components
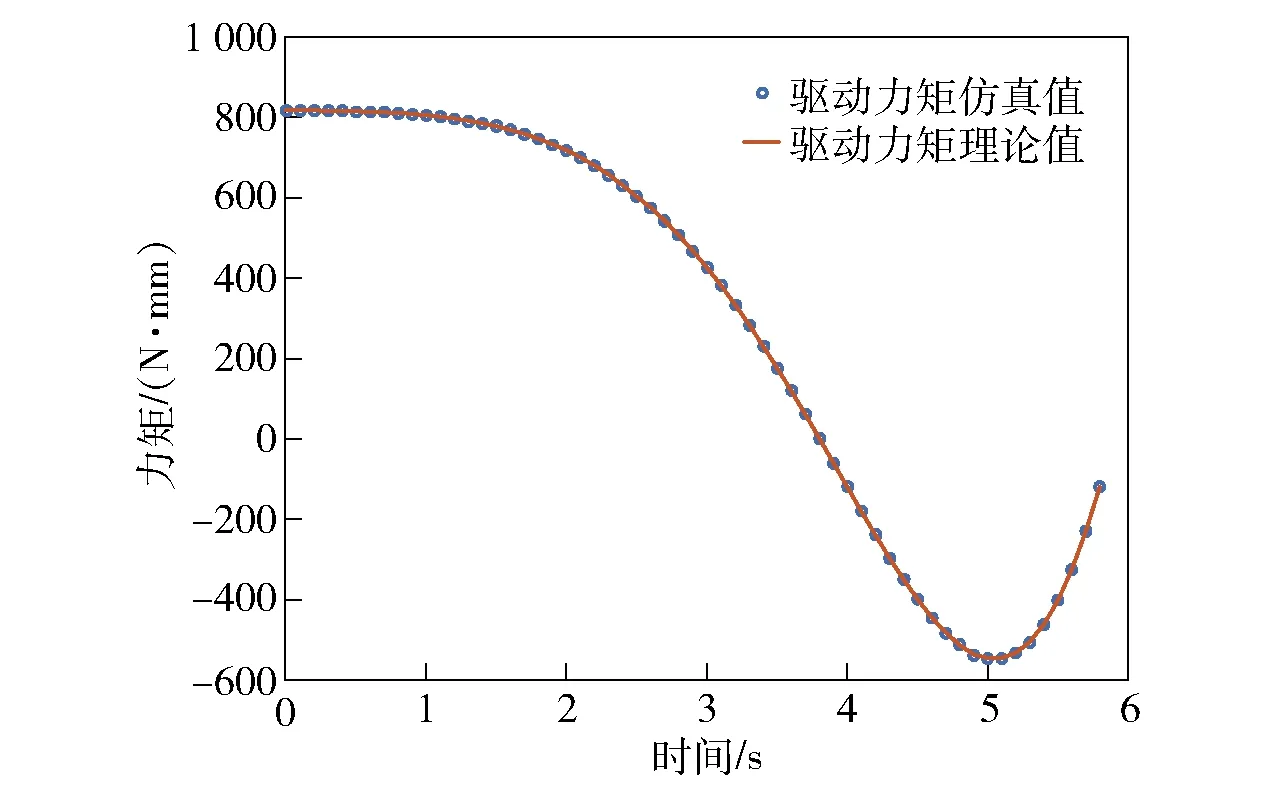
图16 驱动力矩Fig.16 Input driving torque
1) 双层环形桁架式可展天线机构只有一个运动自由度,结构简单,仅需一个驱动便可顺利展开,可较好地用作大型空间天线的支撑和展开机构。
2)基于螺旋理论,分析了双层环形桁架可展天线机构的运动特性,并结合牛顿- 欧拉方程和虚功原理建立了整体动力学模型。这种分析方法物理意义明确,过程较为程式化,易于编程,适用于大型复杂机构的计算与分析。
3) 建立了整体双层环形桁架可展机构的仿真模型,并进行了数值计算与仿真验证,计算和仿真结果验证了本文理论分析的正确性。本文的研究内容可为此类大型复杂空间可展机构的研发设计提供参考。
