基于Winkler基体的滚柱丝杠降维接触模型研究
2020-05-19刘佳彭航罗英张毅雄朱紫豪颜达鹏
刘佳 彭航 罗英 张毅雄 朱紫豪 颜达鹏


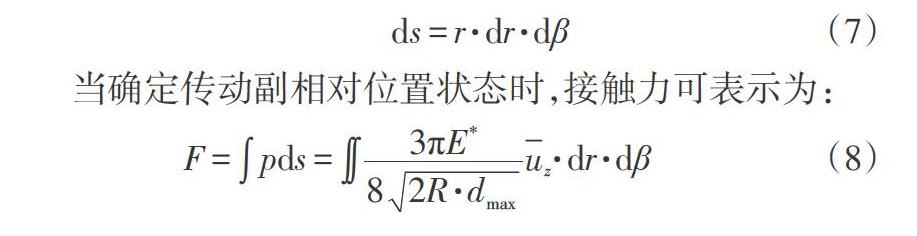
摘 要:本文结合滚柱丝杠传动副结构特点和赫兹接触理论,采用降维法快速求解,基于Winkler基体研究了滚柱丝杠传动副接触模型;通过自编译程序分析了一型滚柱丝杠传动副接触作用力,进行了有限元分析验证。结果表明,该方法可用于滚柱丝杠传动副接触分析,可与赫兹接触方法相结合,为进一步研究滚柱丝杠传动副传动特性奠定基础。
关键词:滚柱丝杠传动副;Winkler基体;接触
中图分类号:TH21 文献标识码:A 文章编号:1003-5168(2020)08-0011-03
Research on Dimension Reduction Contact Model of Planetary Roller Screw Based on Winkler Foundation
LIU Jia PENG Hang LUO Ying ZHANG Yixiong ZHU Zihao YAN Dapeng
(Science and Technology on Reactor System Design Technology Laboratory in Nuclear Power Institute of China,
Chengdu Sichuan 610041)
Abstract: In this paper, combined with the structural characteristics of the planetary roller screw and Hertz contact theory, the dimension reduction method was adopted to solve the problem quickly, and based on Winkler Foundation, the contact model of the planetary roller screw was studied; the contact force of the planetary roller screw was analyzed by self compiled program, and the finite element analysis was carried out to verify the model. The results show that this method can be used for contact analysis of the planetary roller screw, and it can be combined with Hertz contact method to lay a foundation for further study of transmission characteristics of the planetary roller screw.
Keywords: planetary roller screw;Winkler foundation;contact
滚柱丝杠传动副是一种能将旋转运动与旋转运动相互转换的传动机构[1],常见形式如图1所示。由于应用场景不一,该种传动机构的具体结构形式多样,主要结构特点包括轴向中心的丝杠(具备螺纹升角,直径一般比滚柱大)以及周向均布的多个滚柱(具备或不具备螺纹升角,直径一般比丝杠小,轴向长度较丝杠小)。该种传动机构由瑞典科学家Carl Bruno Strandgren于20世纪40年代发明,已发展成为一种广泛应用的优秀传动装置。其核心传动部件为滚柱丝杠,每个滚柱的多个面与丝杠表面接触,接触形式为线接触。该种接触形式与大量广泛应用的滚珠丝杠传动副相比,由点接触变为线接触,传动性能更为优异。
滚柱丝杠传动副的接触问题一直是人们关注的重点和研究的难点,一般常见的分析方法为有限元分析或基于赫兹接触理论开展分析。赫兹接触理论及接触数值解法对滚柱丝杠传动副中的线接触可得到有效解[2],但一般分析复杂。根据弹性力学基本原理,接触表面上一法向作用力会影响该法向力作用点附近区域。当传动副接触表面作用力为分布力时,滚柱丝杠传动副接触表面上接触区域内任一点的位移不仅仅由作用于该点的法向力大小决定,即接触表面任一点的位移取决于接触表面压力分布。因此,如果仅由滚柱表面与丝杠表面的干涉值求解分析干涉位置的法向接触力,困難较大。
针对上述困难,可以采用降维法快速求解[3],基于Winkler基体将三维接触映射到一维接触。Winkler弹性基础或“垫子”的核心思想是接触区域内任一点的位移仅由作用于该点的法向力大小决定,即接触表面任一点的位移取决于接触表面该点处的压力分布情况。本文将采用基于Winkler基体的降维接触模型研究滚柱丝杠接触问题。
1 滚柱丝杠传动副Winkler应力模型
传动副接触时,每一个滚柱丝杠接触面上,滚柱表面轴向方向的接触长度远远大于垂直该方向的接触长度,因此截取垂直于滚柱轴向的接触面为分析曲面,如图2所示。
图2 接触分析截面
在分析视图内,传动副可互相表示为弹性“垫子”,弹性“垫子”设置大量无相互作用垂直于接触表面的弹簧,即忽略传动副内各相邻单元之间的剪切力。模型示意图所图3所示。
可建立接触模型中的传动副接触法向方向的干涉值与弹性位移的关系:
[uz=dmax-x22R] (1)
式中,[uz]为接触区域的弹性位移,mm;[dmax]为丝杠与滚柱接触面中的最大干涉值,也为接触面对称轴处的最大干涉值,mm;x为接触面与接触对称轴的距离,mm;R为接触综合曲率半径,mm。
其中,接触区域边缘有弹性位移[uz],大小为0,由此可知:
[b=2R·dmax12] (2)
式中,[b]为半接触宽度,mm。
根据弹性力学基本原理可得,接触范围内任一点的接触压力(接触应力)为:
[px=K·uzh] (3)
式中,[K]为基础弹性模量或弹簧刚度;[h]为基础深度。
对式(3)在接触范围内进行积分,可得接触轴向方向上单位长度的线接触力,即
[P=-bbpxdx=Kh-bbdmax-x22Rdx=2Kb33hR] (4)
本模型中的单位长度线接触力要与基于赫兹理论的分析结果保持一致,由此可得:
[Kh=3πE*8b] (5)
因此,传动副接触范围内任一点接触应力可表示为:
[p=3πE*82R·dmaxuz] (6)
当传动副相对位置固定时,式(6)中[dmax]为已知量,并结合数值求解方式可得任一点的接触深度[uz],即可分析得到任一点的接触应力。
2 滚柱丝杠传动副Winkler接触力模型
基于接触点接触深度与接触应力的关系,为进一步分析滚柱丝杠传动副接触状态(或干涉深度)与接触力之间的关系,考虑在滚柱各齿上齿面选取足够多具有合适相对位置的点,并结合式(1)分析传动副接触区域接触深度,结合式(6)分析各接触点接触应力,最后考虑各接触点所代表的接触微元区域面积,求出微元接触力,再求出当前传动副状态下的接触力。
考虑到滚柱为旋转体,以滚柱轴线中心面所在柱坐标进行分析,选取滚柱接触面上任一点[Ar,β,z],且相邻两点之间半径、角度差值为定值[dr、dβ],因此任一[A]点所表示的面积可表示为:
[ds=r·dr·dβ] (7)
当确定传动副相对位置状态时,接触力可表示为:
[F=pds=3πE*82R·dmaxuz·dr·dβ] (8)
3 滚柱丝杠传动副接触力分析
針对单一接触面承载约55 N的滚柱丝杠传动副,采用Winkler接触力模型,通过Matlab编译程序进行传动副接触力分析。分析得出,最大接触深度为0.000 12 mm,最大接触半宽度为0.06 mm,最大接触应力约为270 MPa。与ANSYS软件接触静力学有限元分析结果236 MPa对比分析,误差为14.4%。
4 结论
本文采用基于Winkler基体的降维接触模型及分析方法,研究了滚柱丝杠接触问题,分析结果经过了有限元分析方法验证。结果表明,该方法可用于处理滚柱丝杠传动副接触问题,可与赫兹接触方法相结合,为进一步研究滚柱丝杠传动副传动特性奠定基础。
参考文献:
[1]刘更,马尚君,佟瑞庭,等.行星滚柱丝杠副的新发展及关键技术[J].机械传动,2012(5):107-112.
[2]姚琴,吴立言,刘更,等.行星滚柱丝杠副弹塑性接触分析[J].机械传动,2016(11):106-110.
[3]Popov V L,Hess M.Method of Dimensionality Reduction in Contact Mechanics and Friction[M].Beijing:Tsinghua University Press,2015.
