某单箱双室道岔连续梁偏载效应研究
2020-05-19陈留剑李运生张彦玲
陈留剑, 李运生, 张彦玲
(石家庄铁道大学土木工程学院,河北 石家庄 050043)
薄壁箱型截面因为整体性好、刚度大、节省材料且有较大的抗扭刚度等这些优点而被广泛用于桥梁设计中,但是箱梁桥在偏心荷载下的偏载效应[1]在设计中是不容忽略的。平面设计时,利用偏载系数考虑箱梁在偏心荷载作用下的空间效应,计算偏载系数的方法有经验系数法、偏心压力法和修正的偏心压力法等[1-3]。关于箱梁偏载效应的研究有很多:郭忆、叶见曙等[2]认为箱梁偏载系数简化计算采用修正偏心压力法比较符合实际情况。王勇[3]提出了基于梁肋实际横向分配系数的修正偏心压力法。程翔云[4]提出了两个虚拟弹簧支撑的内力增大系数计算模型。陈爱萍[5]和薛兴伟[6]认为应该建立全桥的三维实体单元模型来计算偏载系数。张德兵[7]认为文献[4]所提出计算模型中两个弹簧刚度可以通过三维梁单元模型直接求出,然后再按文献[4]的方法计算任意一跨的偏载系数。徐敏[8]对偏心压力法、修正后的偏心压力法两种方法和文献[3]提出的计算方法折中考虑提出了一种计算偏载系数的方法。
上述偏载系数的简化计算方法可以应用在箱梁桥的初步设计中。由于铁路道岔连续梁结构形式复杂,为了获取准确的偏载系数,本文利用有限元方法对7×32 m双线变三线单箱双室道岔连续梁的正应力偏载系数、挠度偏载系数和支反力偏载系数的分布规律作了全面的研究。
1 偏载系数的定义
1.1 正应力偏载系数
箱形梁桥在承受偏心荷载作用下,将产生纵向弯曲、扭转、畸变及横向挠曲四种变形[9]。对于桥梁纵向正应力包含三项:纵向弯曲正应力σm、约束扭转翘曲正应力σω和畸变翘曲正应力σdω。现定义正应力偏载系数为
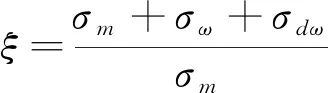
(1)
1.2 挠度偏载系数
箱形梁桥在承受偏心荷载作用下,定义挠度偏载系数为
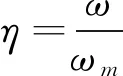
(2)
式中:η为挠度偏载系数;ω为偏心荷载作用下截面任一点处的挠度;ωm为对称荷载作用下截面对应位置处的挠度。
1.3 支反力偏载系数
在实际设计中,每个墩顶设置3个支座,近似认为3个支座的反力相等,所以支反力的偏载系数按式(3)计算。
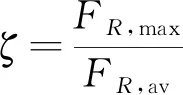
(3)
式中:ζ为支反力偏载系数;FR,max为3个支座反力的最大值;FR,av为3个支座反力的平均值。
2 工程实例分析
2.1 工程概况
某桥为双线变三线道岔连续梁,主梁梁体采用C50混凝土。线路布置如图1所示。

图1 线路布置图(单位:cm)
主梁计算跨度为(31.85+5×32.70+31.85) m。支座中心线至梁端0.75 m,梁全长228.7 m。截面中心处梁高为3.035 m。
主梁截面采用单箱双室、等高度、变截面的斜腹板形式。箱梁顶宽12.60 ~16.10 m,底宽5.5 ~8.8 m。顶板厚度除梁端处及支点处外均为0.40 m;腹板厚0.5 ~0.8 ~1.4 m,按折线变化;底板厚由跨中的0.3 m按折线变化至支座处的0.9 m。全联在梁端支点和跨中支点处共设置8个横隔板。梁端支点处横隔板厚度为1.5 m,跨中支点处横隔板厚度2 m。箱梁两侧腹板与顶板相交处外侧均采用圆弧倒角过渡,倒角半径0.75 m。箱梁底板和腹板相交处外侧采用圆弧倒角过渡,在支点附近倒角半径为0.1 m,其余部位倒角半径为0.3 m。横隔板均设有过人孔,供检查人员通过[10]。
2.2 建立有限元模型
利用Midas FEA建立全桥有限元模型,采用实体单元模拟。本桥利用Midas FEA直接建立网格的方法建立映射网格,保证了网格的质量,全桥一共476 448个实体单元。连续梁边界条件按在实际支座布置位置处建立节点约束(分别按固定支座、横向支座、纵向支座和多向支座约束相应方向的平动自由度)的方法来处理。模型坐标系,坐标原点位于窄端顶板中心,x轴沿桥梁纵轴线,y轴沿横桥向,z轴沿竖向。为了得到箱梁梁单元模型下的正应力和挠度,利用Midas Civil建立了梁单元模拟的全桥有限元模型,边界条件按单支座来处理,材料与实体单元模型一致,全桥共121个梁单元。
2.3 荷载工况
桥梁为7跨,第6跨和第7跨的桥面宽度较大,在左线和右线同时加载的工况下,第6跨和第7跨偏载效应最为显著,并且应力对设计起控制性作用。按左线和右线双线加载取,以第6跨和第7跨为研究对象,分别研究40#墩和41#墩墩顶箱梁顶板正应力偏载效应,纵向加载图式分别如图2(a)、图2(b)所示;第6跨和第7跨跨中截面顶板和底板正应力偏载效应,纵向加载图式分别如图2(c)、图2(d)所示。横向加载图式如图3(a)所示。

图2 纵向加载图式

图3 横向加载图式
为了满足列车安全平衡运行的要求,《铁路桥涵设计规范》(TB10002-2017)规定:高速铁路在列车竖向静活载作用下梁体引起的轨面不平顺值,在3 m长的线路范围一线两根钢轨的竖向相对变形限值为1.5 mm。由于单线偏载时,轨面不平顺值可能比双线更大,因此对于挠度偏载效应,研究工况按左线和右线双线加载、岔线单线加载两类取,下面对第6跨和第7跨跨中截面的挠度偏载系数进行研究,纵向加载图式分别如图2(c)、图2(d)所示,横向加载图式如图3所示。
桥梁支座布置和选型时,一方面要保证支座的支反力不超过其竖向承载力,另一方面不出现支座脱空现象。由于单线偏载时,支反力可能会出现负值,因此对于支反力偏载效应,研究工况按左线和右线双线加载、岔线单线加载两类取。道岔梁支反力最不利组合为主力+附加力,主力中的恒载主要包括自重、二期恒载和支座沉降,附加力为非线性温度梯度。纵向加载图式分别如图2(e)~图2(g)所示,横向加载图式如图3所示。荷载工况如表1所示。

表1 荷载工况
3 分析结果
3.1 ZK活载作用下的正应力偏载系数
表2中的偏载系数按式(1)确定。由表2可知,双线偏心加载下,箱梁偏载效应显著,墩顶截面比跨中截面严重;梁单元模型的正应力偏载系数取1.2比较合适。

表2 双线加载正应力偏载系数
3.2 ZK活载作用下的挠度偏载系数
在ZK静活载作用下,图4和图5分别为第6跨和第7跨跨中截面挠度。从图4和图5中可以看到,在偏心荷载作用下,箱梁产生了明显的扭转变形。
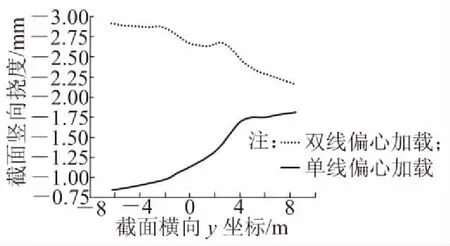
图4 偏心荷载作用下第6跨跨中截面挠度

图5 偏心荷载作用下第7跨跨中截面挠度
由图4和图5可知,在偏心荷载作用下,箱梁两侧翼缘的挠度最大差值为1.08 mm。截面两侧翼缘的挠度偏载系数按式(2)确定,计算结果如表3所示,单线偏载效应比双线显著。一线两根钢轨的竖向相对变形如表4所示,双线偏心加载下,岔线两根钢轨的竖向相对变形较大;单线偏心加载下,左线两根钢轨的竖向相对变形较大。由表4可知,在ZK静活载偏心作用下,一线两根钢轨的竖向相对变形满足规范要求。

表3 挠度偏载系数
表4 一线两根钢轨的竖向相对变形mm

工况右线左线岔线工况右线左线岔线70.110.140.3280.100.160.2790.140.440.19100.120.420.20
3.3 ZK活载作用下的支反力偏载系数
3.3.1 双线(两条正线)偏心加载
按照工况11~工况13分别研究40#、41#和42#墩支反力的偏载情况,偏载系数按式(3)确定。工况11~工况13下的支反力和偏载系数如表5所示,工况11~工况13分别与恒载和非线性温度梯度叠加后的支反力如表6所示。
由表5可以看到,双线偏心加载下,支座的偏载效应不容忽视。42#墩支座的偏载系数最大,达到1.69。
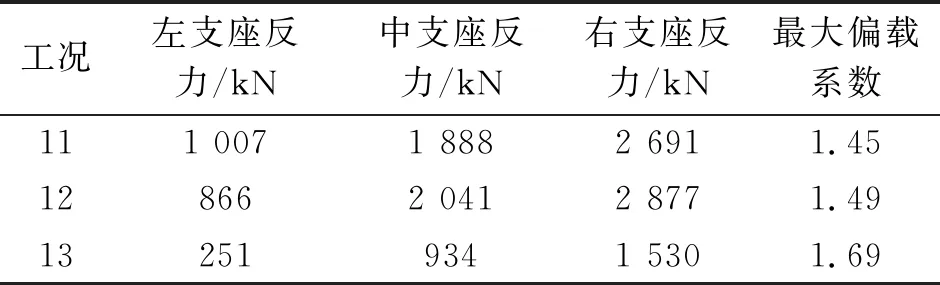
表5 双线偏心加载下的支反力和偏载系数

表6 恒载+非线性温度梯度+双线偏心加载下的支反力 kN
3.3.2 单线(岔线)偏心加载
按照工况14~工况16分别研究40#、41#和42#墩支反力的偏载情况。偏载系数按式(3)确定。工况14~工况16下的支反力和偏载系数如表7所示,工况14~工况16分别与恒载和非线性温度梯度叠加后的支反力如表8所示。

表7 单线偏心加载下的支反力和偏载系数

表8 恒载+非线性温度梯度+单线偏心加载下的支反力 kN
在单线(岔线)偏载加载时,在3种工况下,每个桥墩的右支座均出现了负支反力,42#墩的左支座偏载系数为最大,达到了3.10,显然单线偏心加载比双线偏心加载偏载效应严重。
由表8可以看到,40#墩、41#墩、42#墩的支座均没有出现脱空。
4 结论
工程实例中,在双线偏心荷载作用下,最大的正应力偏载系数为1.206,可见传统的正应力经验偏载系数1.15已经不能适用该工程实例的情况。
在双线偏心荷载作用下,挠度偏载系数为1.120,支反力偏载系数为1.69;在单线偏心荷载作用下,挠度偏载系数为1.388,支反力偏载系数为3.1。因此在挠度验算和支座吨位选取时,需要考虑活载的偏载效应。
在实际设计中,如果之前没有可以借鉴的类似桥梁设计例子,建议采用板壳或实体单元模型获取准确的偏载系数。
