基于三角模糊云贝叶斯网络的盾构下穿段施工风险评估

陈洪波， 王 宁， 王建西

(1.中铁投资集团有限公司，北京 100160；2.石家庄铁道大学道路与铁道工程安全保障教育部重点实验室，河北 石家庄 050043)

近年来，地铁施工引起的既有老旧建筑沉降、开裂、倾斜等破坏对城市公共安全构成极大威胁。前人采用传统方法针对不同情况下地铁邻近建筑物的施工安全问题开展了大量研究。然而，地铁施工风险因素往往表现出显著的不确定性和动态性特征。贝叶斯网络在描述事件不确定性、知识表达和动态推理方面具有显著优势。相关研究虽然取得了一定成果，但施工中大量风险因素往往难以监测，获取的风险数据包含较大模糊不确定性。三角模糊数和云模型是合理考虑评估数据的模糊性与不确定性的有效方法。

本文首先将三角模糊数与云理论相结合，研究定性评判向定量概率分布转化的方法。然后，基于层次分析法、状态影响因子和云模型得到贝叶斯网络条件概率。最后，构建施工风险评价贝叶斯网络模型，为盾构下穿施工安全风险预控提供理论依据。

1 三角模糊云模型与贝叶斯网络

1.1 基于三角模糊数的云模型建立

1.1.1 云模型相关概念

云模型是大数据和人工智能领域中进行不确定性分析的强有力工具，可实现定性与定量的相互转换。

定义1[1]：设对象X的定性论域为C，Z是论域上的一个定性概念集合，若对于C上的一次随机定量实现x，有μ(x)∈[0,1]，则x在C上的分布称为云，μ(x)被称为确定度，x表示该云的一个云滴。

期望Ex、熵En和超熵He是云的3个数字特征。若x为正态云的云滴，则x～N(Ex,En′2)，其中En′～N(En,He2)，x对Z的确定度满足：

(1)

期望Ex表示云滴分布的中心点，反映了对定性概念认知的统一性和稳定性。熵En是定性概念随机不确定性的度量，反映云滴分布具有模糊特征。超熵He的直观反映是云滴厚度，其值越大则云层越厚，它由熵的随机性和模糊性共同决定。

利用正态云发生器式(1)，可将定性概念转换为定量的随机数据，即产生一定数量的云滴。相反，逆向云发生器可以统计得到云的数字特征，从而进行定性评价，如式(2)所示：

(2)

1.1.2 风险评价的三角模糊数表示

实践中，模糊随机事件很难用确定的数值量化，为此引入三角模糊数描述事件风险概率等级。

定义2：设论域C上的模糊集为Z，若μZ(x)∈[0,1]是x在Z上的映射函数，表示为上限u、下限l和模态值m的线性函数，称为三角模糊隶属函数。

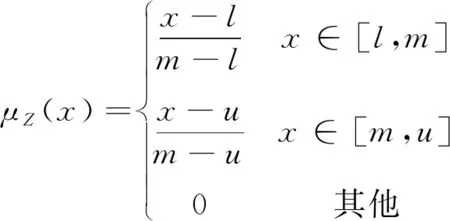
(3)

本文依据《城市轨道交通地下工程建设风险管理规范》定义的风险发生概率P特征集将风险事件概率等级分为5级， 表1给出了各标准等级的分值区间[Cmin,Cmax]及三角模糊数。

表1 风险指标标准等级划分与三角模糊数

1.1.3 三角模糊数的云模型转化

利用三角模糊数能够方便地实现被评价对象的度量，使定性语言值转化为具体的数量，然而，模糊运算规则处理评价数据时容易导致信息损失。云模型通过对生成的大量云滴进行统计分析，具备强大的模糊不确定性数据推理能力。为此，将三角模糊数转化为云模型，实现风险事件不确定性数据运算。

①生成数据样本。利用公式(3)在区间[l,u]内随机抽样，产生包含三角模糊数所表达的不确定和模糊信息的n个样本点(xi,μZ(xi))。②计算云数字特征，利用公式(1)得到均值Ex、熵En和超熵He。③利用正态云发生器生成云。

1.1.4 概率分布的计算

在云模型中，云滴构成的云团对论域中每个定性概念的贡献是不同的，云团越密集则对该概念的支持也越大。设一维论域C的任一小区间上的云团为△x，它对概念Z的贡献为：

(4)

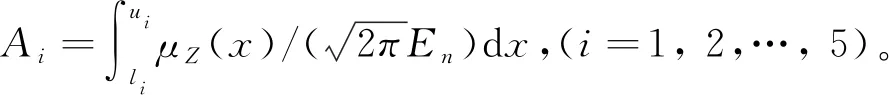
1.2 贝叶斯网络模型

1.2.1 条件概率表建立

贝叶斯网络可记为有向非循环图BN=(G,P)，节点表示事件，构成网络图模型G，条件概率表CPT记为P，用于量化事件间的相互作用。通常，在无法获取风险指标大量数据时需借助专家经验建模。为确保合理性，本文利用层次分析法和状态影响因子评判风险指标的相互影响，再利用云模型生成条件概率表CPT。

考虑到风险指标(父节点)的不同等级状态对下一层指标(子节点)的影响程度不同，通过专家评判法分别确定每个父节点不同状态对子节点的影响值Sij∈ [0, 10]，得到状态影响因子矩阵S=(Sij)n×5。将n个父节点的各个状态进行遍历，依据节点权重和状态影响因子得到云模型的数字特征，计算公式为：

(5)

式中：j为节点的状态循环变量，j=(1, 2,…, 5)；l为父节点的状态组合个数；k反映了专家评估随机性，结合实际情况选取k=0.2。根据均值Ex、熵En和超熵He，利用云发生器和概率分布计算方法即可确定节点的条件概率表。

1.2.2 网络推理与敏感性分析

贝叶斯网络可在风险分析的任意阶段，进行预测推理和诊断，如式(6)、式(7)所示。

P(B=b)=∑P(B=b|X1,X2,

…,Xn)P(X1,X2,…,Xn)

(6)

P(Xi=xi|B=b)=

(7)

敏感性分析用于确定风险防控的关键因素集合。假设目标节点变量为Q，证据节点变量为E，利用信息熵计算出节点变量之间关联的互信息(MI: Mutual Info)，如式(8)，其值越大则对相关因素越敏感。

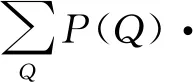
(8)

2 地铁下穿建筑群风险评估模型

2.1 建立风险评价指标集

根据专家咨询并参考文献[2]，识别盾构下穿建筑群的主要风险因素，按照影响关系建立4层评价指标体系，如图1所示。

图1 盾构下穿密集老旧建筑风险评估指标

评估模型中，每个指标因素即为一个风险事件，可参考《地铁工程施工安全评价标准》(GB 50715 - 2011)，按照所提出的三角模糊云模型方法进行定量评价。

2.2 网络模型结构与CPT确定

将风险评价指标集X1～X15的15个因素作为节点，建立网络模型。根据表2所示的指标权重和状态影响因子评价值，利用式(5)计算云数字特征。其中，指标权重采用AHP法，状态影响因子评价由专家评判，以0～10给出不同状态下父节点对子节点的影响评分。

以节点RT为例，将3个父节点M1、M2和M3的重要性进行两两比较，分析得到权重W=[0.549 9,0.240 2,0.209 8]。

将RT父节点各状态进行遍历，依据节点权重和状态影响因子计算云期望EX=[EX1,EX2,…,EX5]，从而得到云数字特征。例如，EX1=0.549 9×2+0.240 2×1+0.209 8×1=1.549。利用云发生器生成1 000个云滴，经过统计分布计算条件概率表。由于RT有3个父节点，每个节点有5个状态，因此，节点CPT共包含125行 54个元素，表3仅给出前10行分布计算结果。按以上方法计算所有节点的条件概率表。模型建立后，即可进行各评价指标实时更新和风险预测，为下穿施工安全提供决策信息。

3 案例研究

3.1 工程背景

表2 风险因素权重及状态影响因子评价表

石家庄地铁2号线东三教站～东岗头站区间设计为盾构法，K28 + 413.349～658.416段下穿平安小区，隧道顶距建筑物基础15.5～16.5 m。该段地层为粉细砂、粉质黏土，砂层中密～密实，稍湿，中～低压缩性。地下水类型为潜水，埋深约38 m，位于隧道底板以下。

施工区周边分布多个建筑群。其中，平安小区有8栋老旧建筑物，经鉴定房屋均为Du级(危险级)。其中1#、2#、9#楼(均为3层房屋，共131户)建于20世纪五六十年代，条形石砌基础，无圈梁、结构柱等抗变形结构，保证下穿施工安全是风险管控的难点。为此，选取平安小区2#楼作为分析对象进行动态风险评估。

3.2 证据数据收集与处理

编制施工风险指标评分表，邀请业内专家逐项评价。通过勘察、施工和监测资料，由专家给出三角模糊评价值，如表4所示。采用1.1.3节的方法将其转化为云模型，计算数字特征和各风险因素的概率分布结果。

表3 基于状态影响分析结果和云模型生成节点RT的CPT

表4 风险因素专家评分结果

图2给出了风险指标X1的三角模糊云及综合云。根据综合云统计云团对风险概率等级的贡献度，得到X1的概率分布计算结果为p=[0.217 1,0.469 0,0.237 0,0.077 0,0]。按照相同的方法计算其余因素的概率分布，将上述节点概率数据输入贝叶斯网络进行推理。

图2 风险因素X1专家评判三角模糊云和综合云

3.3 结果分析

3.3.1 风险发生概率分析

图3为不可观测风险因素节点各状态等级的分布概率堆叠柱状图。为便于比较，将节点状态概率pstate(i)与状态等级Ii加权求和，计算综合风险概率等级Iave，绘于图3中。

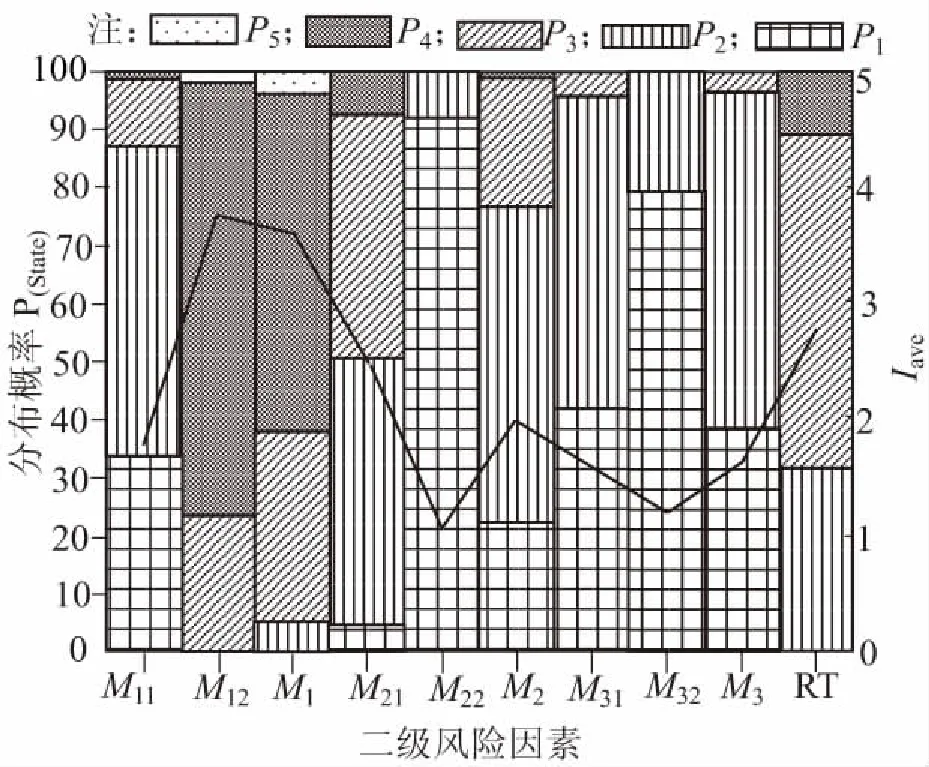
图3 不可观测节点各状态等级分布概率堆叠柱状图

通过Iave值比较发现，在二级风险因素M1、M2和M3中，M1发生概率最高。观察曲线和柱状图可知，潜在风险隐患主要来源于M12周边建筑环境。该下穿施工区域内建筑结构整体性较弱、建筑密集且年代久远，近距离施工增加了事故的可能性。

由于注浆量控制X6和土仓压力参数不合理X8的影响，M21的风险发生概率大于M22，导致M2盾构施工参数风险概率增加。M3施工组织管理与应急状况的风险概率处于较低水平，“不可能”和“罕见”的分布概率之和超过了“96.09%”，综合风险概率等级为1.653 9。M31施工管理综合风险概率等级为1.624，高于M32监控与应急。

3.3.2 盾构下穿施工风险评价

依据《规范》定义风险损失C特征集ΩC=[可忽略，需考虑，严重，非常严重，灾难性]，分别以Cl(l=1～5)表示。利用风险矩阵得到5级风险分级标准，如表5。为了便于施工风险决策，结合工程风险管控实际，参考文献[3]，建立表6所示的风险可接受准则。

表5 风险矩阵及分级

表6 风险接受准则

针对基本风险因素和施工总体风险进行风险损失专家评估，结果见表7。利用表5，将各因素风险损失对应列的概率分布与风险等级相乘后求和即可得到风险等级大小，如图4所示。

表7 风险损失等级专家评价

图4 基本风险因素风险等级评估结果

由图5可见，风险等级超过Ⅲ级的因素为X4和X12，占总数13.3%。分析可知，由于施工区域地表住宅建于上世纪中期，为使用超过60 a的老旧建筑，X4建筑使用年限的风险等级接近Ⅳ级，需采取技术措施将其施工风险转移并控制在可接受范围。施工安全事故常与作业中的不当操作、技术措施不合理等人为因素相关，X12班组安全培训和考核的风险评估结果略超过Ⅲ级——“可接受”水平，施工中应强化作业班组安全培训，降低人为操作失误风险。

风险等级接近Ⅲ级的因素共8个，约占53.3%。按风险大小依次为X6、X5、X9、X8、X3、X14、X15和X7。X5近接施工距离和X3基础埋深与结构类型由客观设计因素决定，其风险处于可接受范围。在技术方面，X6注浆量控制是减少地层损失和预防沉降的关键，需要采取有效措施降低风险。分析结果揭示，出现X9刀盘和刀具磨损可能性也较大，这与砂卵石类地层长距离掘进易发生刀具磨损的工程经验相一致。X8为土仓压力参数设置，由于地表建筑附加荷载作用，下穿时应做好优化调整，保证合适的土压力。此外，还应对X14危险源监控、X15应急处置与风险控制、X7推进速度不合理因素做好控制防范。

盾构下穿风险节点RT的风险概率等级后验分布p= [1.242%,30.345%,57.133%,11.253%,0.027%]。由于潜在风险损失等级为C4(非常严重)，取表5第2列计算综合风险水平R= (0.012 4×2+0.303 4×3+0.571 3×3+0.112 5×4+0.000 27×4)=3.100 4，略超Ⅲ级。根据风险可接受准则，盾构下穿建筑群段施工风险总体可接受，但需引起重视并做好防范措施。

3.3.3 敏感性分析

通过Netica软件计算盾构下穿建筑群风险节点RT与所有父节点的互信息，其值越大则对RT影响越敏感，见表8。按照因素敏感性由高到低、风险等级由大到小的顺序排列，得到图5所示的分布图。显然，越靠近左下角则该风险因素越重要，除X4、X5、X1和X3无法规避外均为可控风险因素，施工时应优先采取针对性的处置措施。

图5 敏感性与风险排序分布图

4 结论

(1)将三角模糊数和云理论相结合，提出了定性评判转化为定量概率分布的方法。该方法充分利用了二者在模糊定性表达与定量转化方面的优势，为风险不确定性数据处理提供了有利工具。

表8 盾构下穿诱发事故风险敏感因素分析

(2)引入层次分析与状态影响因子成功考虑了父节点权重和不同状态对子节点的影响，并通过生成随机风险云和统计分析方法建立条件概率表。

(3)构建了盾构下穿施工风险评价指标体系和三角模糊云贝叶斯网络模型。应用表明，该模型的风险推理结果与实际吻合，为现场提供了科学准确的决策信息。