基于Adaboost集成模型的城市短期供水量预测方法
2020-05-19高赫余吴潇勇
高赫余,王 圣,吴潇勇
(上海城投水务<集团>有限公司供水分公司,上海 200444)
供水量预测分为长期预测和短期预测,长期预测是指对未来一周、一个月乃至一年的预测,而短期预测可以细化到未来1 h、1 d的预测[1]。本文主要研究的是短期预测,即日供水量预测和时供水量预测。在管网中水压和供水量能满足用户的前提下,根据模型所预测的日与时供水量优化供水模式,使水管网在能耗最小、漏损最小的情况下,保证给水质量,同时,能够达到优化调度的目的[2]。
由于我国需水量数据可靠性低,且时间系列较短,用传统的预测方法如灰色预测、时间序列[3]、回归分析以及定额法等不仅工作量大,精度也很难保证[4]。随着现在计算机硬件及软件的发展,机器学习和深度学习模型已经广泛地应用在工业界中。如王盼等[5]采用随机森林算法构建需水预测模型;BAI等[6]采用多尺度相关向量回归方法构建城市日供水量需求预测模型;郭冠呈等[7]采用双向长短时神经网络构建了短期供水量预测;SHABANI等[8]通过对混沌时间序列进行相空间重构,并结合支持向量机模型构建城市水量需求预测模型。这些回归模型能高精度的拟合非线性函数,从而能在训练样本上得到预测结果,但是,易引发过拟合,泛化性能较差,在测试样本上往往不理想,无法在实际中得到较好的推广应用。
目前,集成学习在工业界和学术界受到越来越多的关注,所谓集成学习即训练多个弱回归模型,对最终的结果进行联合决策[5]。目前,集成模型主要有Bagging策略、随机森林模型、Adaboost等策略。其中,随机森林中,各个决策树相互独立,每个决策树在样本堆里随机选一批样本,随机选一批特征进行独立训练,各个决策树之间无联系;Bagging是在决策树的基础上并行生成一系列决策树,相比于随机森林,Bagging是选取全部特征属性进行训练;相比于以上两种流行的集成模型,Adaboost模型建立的多个弱学器之间均相互联系,使得最终的预测值尽量接近真实值,且有很强的泛化能力[9]。本文首次采用Adaboost集成模型构建水量预测模型,通过对供水量原始数据的预处理,并引入天气、日期、空气质量以及人为构造的属性等信息[10],使模型具有更好的泛化能力。与传统的研究方法如BP神经网络模型[11-14]、决策树模型、随机森林模型、支持向量机模型[8]相比,Adaboost模型的精度和效率更高。
1 回归建模
1.1 Adaboost模型
Adaboost 算法是机器学习中一种重要的特征分类算法,主要解决分类问题和回归问题。目前,该算法已经运用到电力系统负荷预测、交通量预测,得到了不错的预测效果。
Adaboost 算法通过对同一个训练集训练不同的弱学习器,然后将这些弱学习器组合形成强学习器,通过组合使弱学习器互补,从而使组合后的强学习器有较强的泛化能力。其核心思想是重视预测误差大的样本和性能好的弱学习器,即提高训练集中训练效果差的样本权值和学习能力强的弱学习器权值,降低训练效果好的样本权值和学习能力弱的弱学习器权值[15]。
正是由于Adaboost 算法核心思想的特性:重视预测误差大的样本和性能好的弱学习器,对于基础数据不够完善、不够准确、不够丰富的数据集有很好的适用性,能够在水务行业短期供售水量的预测中取得较好的应用效果。
1.2 评价标准
对于水量预测,本文研究更加关注预测的结果和真实的供水量之间的误差大小,因此,采用平均绝对值误差(mean absolute error)作为评价指标,数学定义如式(1)。
(1)
其中:nsamples——样本数量;
yi——真实值;

另外一种可作为参考的指标为平均相对误差(mean relative error),数学定义如式(2)。
(2)
2 日水量预测模型
2.1 数据描述
本节水量数据来源于上海市城投水务(集团)有限公司供水分公司,自2015年11月3日—2019年11月30日共1 489条日供水数据。
上海市城投水务(集团)有限公司供水分公司包括黄浦区、徐汇区、长宁区、闵行区、杨浦区、虹口区、闸北区、普陀区、宝山区、松江区、青浦区11个行政区的全部或部分地域,下设11个供水管理所、36个供水管理站,供水面积高达1 034 km2,在装表数450余万只,供水管网总长16 205 m。
考虑到原始数据所包含的特征只有供水日期,单一的特征会造成较差的拟合结果。因此,本文进一步考察并挖掘影响供水量的多方面因子,同时,将日期信息进一步细化,对特征进行组合扩展,衍生出一系列影响供水量的特征,结合这些特征因子和实际供水量训练Adaboost模型。
图1为该市实际供水量的变化情况。由图1可知,该市供水量为300万~500万t,且不具有周期性,局部波动较大,与日期之间无明显的线性关系,因此,需挖掘其他影响因子。

图1 供水量趋势Fig.1 Trend of Water Supply Demand
2.2 供水因子的选取与解释
2.2.1 异常数据处理
2015年11月3日—2016年3月1日的数据,由于上海市几十年一遇寒潮的影响,波动非常剧烈,不具备普遍规律予以删除。对于缺失的数据,采用以下补全方法:
(a) 对于某一天数据的缺失,以这一天前后两天的平均值代替;
(b) 对于某两天水量差距巨大的数据,这两天的数据以这两天数据的平均值代替。
2.2.2 特征选取
本节研究的重点是日供水量预测,根据预测结果调整每天的供水调度,所以,需要挖掘对供水量有影响的因子。结合以上考虑,本文考察了星期、月、日、四季、日最高温度、日最低温度、日平均温度、天气、转天气、风向、风力、空气质量指数、空气污染程度、节假日情况这14个影响因子,同时,根据人为构造,对数据进行深度挖掘,定义了温度等级、温差、取对数、开根号、求E、多项式运算6个影响因子,且将日期信息深度挖掘,可从日期中抽取该日期属于一周内的第几天、一个月内的第几天、一年内的第几天3个影响因子。通过特征扩展,将原本单一的特征构造为22特征,即星期、月、日、四季、日最高气温、日最低气温、日平均气温、天气、转天气、风向、风力、节假日、空气质量指数、空气污染程度、温度等级、取对数、开根号、多项式、Day_of_week、Day_of_month、Day_of_year、温差等。
考虑到特征的相关性,通过Pearson相关系数法计算得到各特征与水量之间的相关性,并通过相关较高的数值型变量进一步挖掘得到取对数、开根号、求E及多项式4维特征值,由于现有特征维度未必能够充分地描述目标变量,通过现有数据构造新特征。此方法叫做特征构建,用于扩大特征维度,从而尽可能的提高预测精度。
2.2.3 Pearson相关系数
Pearson能帮助理解特征和响应变量之间关系的方法,该方法衡量的是变量之间的线性相关性,结果的取值为[-1,1], -1表示完全的负相关,+1表示完全的正相关,0表示没有线性相关。本文采用Pearson相关系数检验各个特征与观测值之间是否存在线性关系。一是Pearson速度快,易于计算;二是通过Pearson相关系数筛选特征可以降低特征维度,在实际应用中便于使用[16]。
2.3 试验及结果分析
2.3.1 特征确定
通过Pearson相关系数计算特征相关性,并对其中高度相关的特征数据进行深度挖掘。图2为不同特征与供水量之间的相关性指数(对于负相关的特征取其绝对值)。
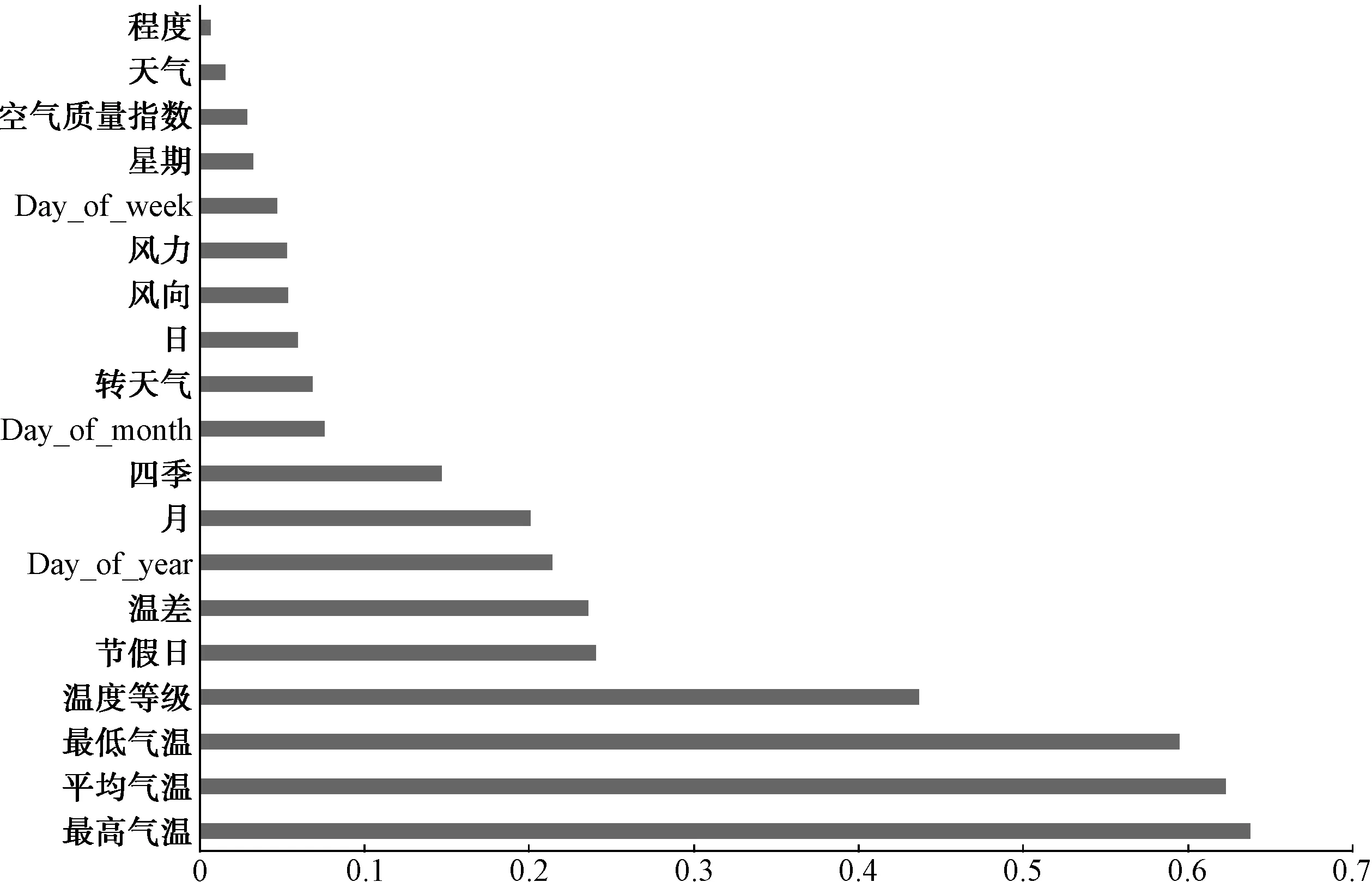
图2 Pearson相关系数Fig.2 Pearson Correlation Coefficient
表1为不同的相关系数对应的相关性。

表1 相关性Tab.1 Correlation

通过深度挖掘构造的4维特征通过Pearson相关系数法计算后得到较好的相关性(图3),可以最终使用。
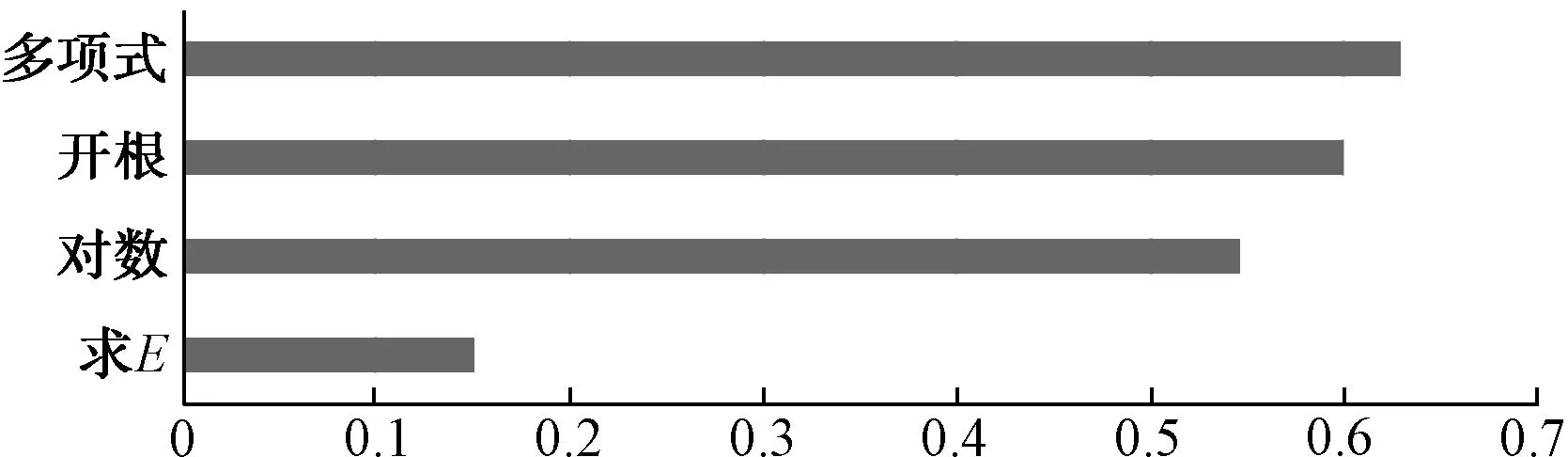
图3 Pearson相关系数Fig.3 Pearson Correlation Coefficient
通过图2及图3相关性计算结果,选取相关系数大于等于0.15的特征,最终得到13维特征:最高气温、平均气温、最低气温、温度等级、节假日、温差、月、四季、开根号、取对数、求E、多项式、Day_of_year。
2.3.2 结果比较
将整体数据划分为测试集和训练集。分别使用决策树[17]、BP神经网络、支持向量机、随机森林,以及Adaboost建立水量预测模型。对于相同的测试集,不同的模型有不同的拟合曲线,分别计算以上5种模型的相关统计量。表2为各种模型在测试集上的平均相对误差和平均绝对误差。

表2 结果比较Tab.2 Comparison of Results
由表2可知,在相同的测试集上,Adaboost表现结果最佳,平均绝对误差为65 817 t,平均相对误差为0.015,与其他4种传统模型相比有较大的提升。
验证的结果表明,Adaboost平均预测误差为65 817 t/d,平均相对偏差为1.5%。与现在流行的BP神经网络和随机森林预测模型相比有显著的提升,平均绝对误差分别降低44 602 t和8 952 t,平均相对误差分别降低1.0%和0.3%。
3 时水量预测模型
3.1 数据描述
本节水量数据均来源于上海市城投水务(集团)有限公司供水分公司,自2017年01月01日—2019年6月30日共21 864条时供水数据,每天从1时—24时共24条数据。
原始数据所包含的特征只有供水日期,单一的特征会造成较差的拟合结果。因此,本文进一步考察并挖掘影响供水量的多方面因子,同时,将日期信息进一步细化,对特征进行组合扩展,衍生出一系列影响供水量的特征,结合这些特征因子和实际供水量训练Adaboost模型。
3.2 供水因子的选取与解释
本节研究的重点是时供水量预测,根据预测结果调整1 d之内每小时的供水调度,所以需要挖掘对供水量有影响的因子。结合以上考虑,本文考察了四季、星期、月、日、时间、小时气温、最高气温、最低气温、平均气温、天气、转天气、风向、风力、空气质量指数、空气污染程度、节假日情况16个影响因子,同时,根据人为构造,对数据进行深度挖掘,定义了气温等级、时温度等级、取对数、开根号、求E、多项式运算6个影响因子,并将日期信息深度挖掘,可以从日期中抽取该日期属于一周内的第几天、一个月内的第几天、一年内的第几天3个影响因子。通过特征扩展,将原本单一的特征构造为25维的特征,即:星期、月、日、四季、最高气温、最低气温、平均气温、天气、转天气、风向、风力、节假日、空气质量指数、空气污染程度、温度等级、取对数、开根号、多项式、Day_of_week、Day_of_month、Day_of_year、小时气温、求E、时间。
考虑到特征的相关性,通过Pearson相关系数法计算得到各特征与水量之间的相关性,并对小时气温特征进一步挖掘得到取对数、开根号和求E这3个特征值,对相关性较高的数值型变量进行多项式计算,得到1个特征值。
通过Pearson相关系数计算特征相关性,并对其中高度相关的特征数据进行深度挖掘,图4为不同特征与供水量之间的相关性指数(对于负相关的特征取其绝对值)。
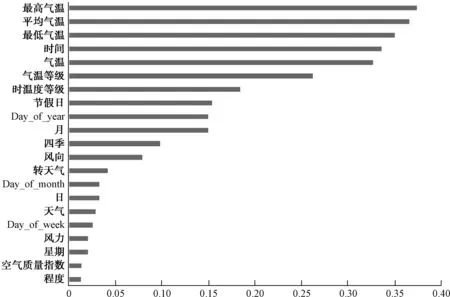
图4 Pearson相关系数Fig.4 Pearson Correlation Coefficient

选取相关性最强的前3个特征,进行多项式运算得到:多项式=3×最高气温+2×平均气温+最低气温。
通过Pearson相关系数法计算得到开根号、取对数、求E和多项式运算4维特征有较好相关性,可以最终使用。通过图4及新构造特征相关性计算结果,选取相关系数大于等于0.15的特征,最终得到的13维特征:最高气温、平均气温、最低气温、温度等级、节假日、气温等级、气温、时间、开根号、取对数、求E、多项式、Day_of_year。
3.3 结果比较
将整体数据划分为测试集和训练集。分别使用决策树[17],线性回归,支持向量机,随机森林,以及AdaBoost建立水量预测模型。对于相同的测试集,不同的模型有不同的拟合曲线,分别计算以上5种模型的相关统计量。表3为各种模型在测试集上的平均相对误差和平均绝对误差。
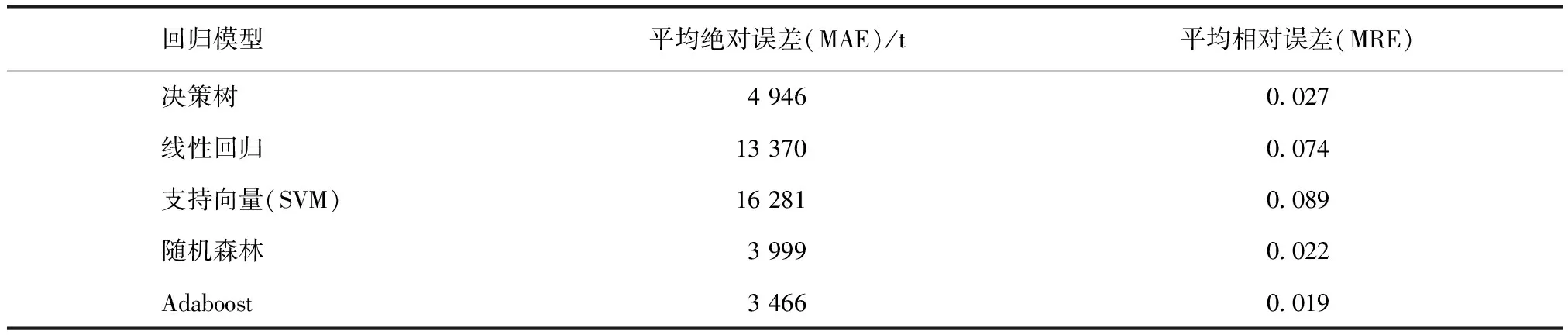
表3 结果比较Tab.3 Comparison of Results
验证的结果表明,Adaboost平均预测误差为3 466 t/h,平均相对偏差为1.9%。与现在流行的决策树和随机森林预测模型相比有显著的提升,平均绝对误差分别降低1 480 t和533 t,平均相对误差分别降低0.8%和0.3%。
4 结语
上述日水量模型和时水量模型的建模通过特征选取、相关性分析和数据建模3个核心步骤,得到较高精度的模型。其中,特征选取所确定的特征因子均为天气、温度和日期等与供水量息息相关的公司外部数据,相对于以往通过历史水量数据增长率简单的预测未来水量和通过员工经验进行供水调度的方式,此模型具有客观、动态、准确、方便和快速的特征,最后数据建模通过横向对比突出了Adaboost 算法在短时供水量预测中的优越性。
通过此模型进行短期的供水量预测,可以根据天气、气温和日期等影响用户用水习惯的因素准确快速计算得到未来1 h和1 d的供水量,依据模型数据,配合老员工的经验合理供给区域内水量及水量调度,可以减少水量损失,提高经济效益。
