Hom-δ-李三系的若干性质

陈 明，易 阳，唐玉玲，陈良云

(东北师范大学 数学与统计学院，长春130024)

0 引言

李三系最早出现在Cartan对黎曼几何的研究中.在[1]中，Jacobson首先介绍并利用了李三系的概念来研究在三元交换子[[u；v];w]下封闭的结合代数的子空间.Lister在[2]中证明了特征为0的李三系的结构理论.至于Hom-型代数的一 些结果也已由文献[3-6]给出在[7]中，Yan介绍了Hom-李三系的概念.Hom-李三系是李三系的推广，它经典的三元Jacobi恒等式由两个线性映射扭曲生成.李三系是Hom-李三系的特殊情形其中两个扭曲映射都取成恒等映射.

在[8]中Leger和Luks研究了李代数的广义导子代数，得到了广义导子代数和它们的子代数的一些重要性质.特别地，他们研究了广义导子代数的结构并且描述了李代数满足的特殊条件.同时他们还指出了李代数的拟导子和上同调之间存在的某种联系.对于更一般的非结合代数的广义导子代数，请读者参考[9-20].

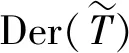
1 预备知识

定义1.1[7]Hom-李三系(T，[.，.，.]，α=(α1，α2))是由域F上的向量空间T，三线性映射[.，.，.]：T×T×T→T和两个线性映射αi：T→T对于i= 1，2 (被称为扭曲映射)组成，使得对于任意x，y，z，u，v∈T，满足

(1)[x，x，z]=0，

(2)[x，y，z]+[y，z，x]+[z，x，y]=0，

(3)[α1(x)，α2(y),[z，u，v]]=[[x，y，z]，α1(u) ，α2(v)]+[α1(z)，[x，y，u]，α2(v)]+

δ[α1(z)，α2(u)，[x，y，z]].

特别地，若α=α1=α2保持括积(i.e.a[x，y，z]=[α(x)，α(y)，α(z)]，∀x，y，z∈T)，则称(T，[.,.,.]，α)为保积Hom-δ-李三系.

定义1.2Hom-δ- 李三系(T，[.,.,.]，α=(α1,α2)，δ)是由域F上的向量空间T.三线性映射[.,.,.]：T×T×T→T和两个线性映射αi∶T→T对于i=1，2(被称为扭曲映射)组成，使得对于任意的x，y，z，u，u∈T，有

(1) [x，y，z]=-δ[y，x，z]，δ=±1，

(2) [x，y，z]+[y，z，x]+[z，x，y]=0，

(3) [a1(x) ，a2(y),[z，u，v]]=[[x，y，z]，α1(u)，α2(v)]+[α1(z)，[x，y，u]，α2(v)]+

δ[α1(z)，α2(u)，[z，x，y]]=0.

定义1.3令(T，[.，.，.]，α，δ)是保积的Hom-δ李三系且定义由T上的线性映射D构成的End(T)的如下子空间U，

U={D∈End (T)|Dα=αD}，

和

[D1，D2]=D1D2-D2D1，

对任意的D1，D2∈U.

定义1.4令(T，[.，.，.]，α，δ)是保积的Hom-δ李三系.线性映射D∶T→T被称为T的ak-m-导子(这里k∈N，k≥0)，使得任意的x，y，z∈T满足：

Dα=αD，

δm[D(x)，αk(y)，αk(z)]+δm[αk(x)，D(y)，αk(z)]+δm[αk(x)，αk(y)，D(z)]=D([x，y，z|)，(1-1)

δ=±1.

记Derαk，m(T)为所有αk-m-导子所构成的集合，则Der(T)=⊕k≥0Derαk，m(T)提供换位子和下述映射：

Der(T)是U的Hom-δ-子代数且被称为T的导子代数.

定义1.5自同态D∈End(T)被称为T的αk-m-广义导子，若存在三个自同态D′，D″，D‴∈End(T)使得对于任意的x，y，z∈T满足：

Dα=αD，D′α=αD′，D″α=αD″，D‴α=αD‴，

δm[D(x)，αk(y),αk(z)]+δm[αk(x),D′(y)，αk(z)]+δm[αk(x),αk(y)，D″(z)]=D‴([x，y，z])，∀x，y，z∈T，δ=±1.

定义1.6自同态D∈End(T)被称为αk-m-拟导子，若存在自同态D′∈End(T)使得对于任意的x，y，z∈T满足：

Dα=αD，D′α=αD′，

δm[D(x)，αk(y)，αk(z)]+δm[αk(x)，D(y)，αk(z)]+δm[αk(x)，αk(y)，D(z)]=D′([x，y，z]) .

令GDerαk,m(T)和QDerαk,m(T)分别是αk-m-广义导子和αk-m-拟导子的集合.那么

GDer(T)=⊕k≥0,m≥0GDerαk,m(T)，

QDer(T)=⊕k≫0,m≥0QDerαk,m(T).

验证GDer(T)，QDer(T)都是U的Hom-δ-子代数是容易的.

定义1.7若C(T)=⊕k≥0,m≥0Cαk,m(T)，Cαk,m(T)由D∈End(T)组成，其中D∈End(T)且对任意的x，y，z∈T，δ=±1满足：

Dα=αD，

δm[D(x)，αk(y)，αk(z)]=δm[αk(x)，D(y)，αk(z)]=δm[αk(x)，αk(y)，D(z)]=D([x，y，z])，

则C(T)被称为T的αk-m-型心.

定义1.8若QC(T)=⊕k≥0QCαk(T)，其中QCαk(T)∈End(T)组成，且对任意的x，y，z∈T满足：

Dα=αD，

[D(x)，αk(y)，αk(z)]=[αk(x)，D(y)，αk(z)]=[αk(x)，αk(y)，D(z)]，则QC(T)被称为T的αk-拟型心.

定义ZDer(T) ：=⊕k≥0,m≥0ZDerαk,m(T),这里ZDerαk,m(T)由D∈End(T)组成，且对任意的x，y，z∈T满足：

Dα=αD，

[D(x)，αk(y)，αk(z)]=D([x，y，z])=0，

则ZDer(T)被称为T的αk-m-中心导子.

容易验证：

ZDer(T)⊆Der(T)⊆QDer(T)⊆GDer(T)⊆End(T).

2 广义导子代数和Hom-δ-子代数

性质2.1令(T，[.,.,.]，α，δ)是保积Hom-δ-李三系则下面结论成立：

(1)GDer(T)，QDer(T)和C(T)都是U的Hom-δ-子代数；

(2)ZDer(T)是Der(T)的Hom-δ-理想.

证(1)假设D1∈GDerαk,m(T),D2∈GDerαs,n(T)，对任意的x，y，z∈T，有

=[(D1α)(x)，αk+1(y)，αk+1(z)]

=α[D1(x)，αk(y)，αk(z)]

[D1D2(x)，αk+s(y)，αk+s(z)]

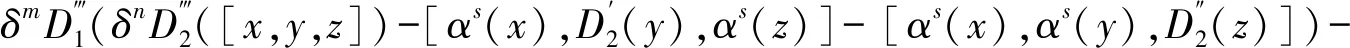
且

[D2D1(x),αk+s(y),αk+s(z)]

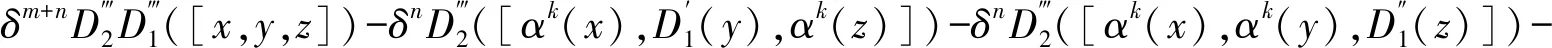
于是对任意的x,y,z∈L,有

[[D1，D2](x)，αk+s(y)，αk+s(z)]

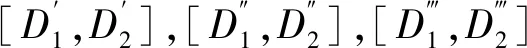
类似地，QDer(T)是U的Hom-δ-子代数.

则[D1,D2]∈Cαk+s,m+n(T)，于是C(T)是U的Hom-δ-子代数.

(2)假设D1∈ZDerαk(T),D2∈Derαs,n(T),对任意的x,y,z∈T,有

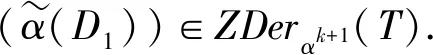
[D1，D2]([x，y,z])=D1D2([x，y,z])-D2D1([x，y,z])

=δnD1([D2(x)],αs(y),αs(z)])+δnD1([αs(x),D2(y),αs(z)])+

δnD1([αs(x),αs(y),D2(z)])-D2([D1(x),αk(y),αk(z)])=0,

且

[[D1，D2](x),αk+s(y),αk+s(z)])

=[D1D2(x),αk+s(y),αk+s(z)])-[D2D1(x),αk+s(y),αk+s(z)]

=D1([D2(x),αs(y)，αs(z)])-δnD2[D1(x),αk(y)，αk(z)])+

[αsD1(x),D2(αk(y))，αk+s(z))]+[αsD1(x),αk+s(y),D2(αk(z))]=0.

则[D1,D2]∈ZDerαk+s,m+n(T)，于是ZDer(T)是Der(T)的Hom-δ-理想.

引理2.2令(T，[.，.，.]，α，δ)是乘法的Hom-δ李三系，则

(1)[Der(T),C(T)]⊆C(T).

(2)[QDer(T),QC(T)]⊆QC(T).

(3)[QC(T),QC(T)]⊆QDer(T).

(4)C(T)⊆QDer(T).

(5)D(Der(T))⊆Der(T),对任意的D∈C(T).

证(1)假设D1∈Derαk，m(T),D2∈Cαs,n(T),对任意的x,y,z∈T,有

[D1，D2]([x，y,z])

=D1D2([x，y,z])-D2D1([x，y,z])

=δnD1([D2(x),αs(y)，αs(z)])-δmD2([D1(x),αk(y)，αk(z)])-

δmD2([αk(y)，D1(y),αk(z)])-δmD2([αk(x)，αk(y)],D1(z)])

=δm+n[D1D2(x)，αk+s(y)，αk+s(z)]+δm+n[αk(D2(x))，αs(D1(y))，αk+s(z)]+

δm+n[αk(D2(x))，αk+s(y),D1(αs(z))]-δm+n[D2D1(x)，αk+s(y),αk+s(z)]-

δm+n[D2(αk(x)),αs(D1(y))，αk+s(z)]-δm+n[D2(αk(x)),αk+s(y),αs(D1(z))]

=δm+n[[D1,D2](x),αk+s(y),αk+s(z)].

类似地，

[D1，D2]([x，y,z])=δm+n[αk+s(x),[D1,D2](y),αk+s(z)]

且

[D1，D2]([x，y,z])=δm+n[αk+s(x),αk+s(y)，[D1,D2](z)].

则[D1,D2]∈Cαk+s,m+n(T)，因此[Der(T),C(T)]⊆C(T).

(2)假设D1∈QDerαk,m(T)，D2∈QCαs(T)，

[D1D2(x)，αk+s(y),αk+s(z)]-[D2D1(x)，αk+s(y),αk+s(z)]

[αk(D2(x)),αk+s(y),αs(D1(z))]-[αs(D1(x)),D2(αk(y)),αk+s(z)]

[αk+s(D2(x)),D2(αk(y),αs(D1(z))]-[αs(D1(x)),D2(αk(y)),αk+s(z)],

[αk+s(x),D1D2(y),αk+s(z)]-[αk+s(x),D2D1(y),αk+s(z)]

[αk+s(x),αk(D2(y)),D1(αs(z))]-[D2(αk(x)),αs(D1(y)),αk+s(z)].

因此

[[D1,D2](x),αk+s(y),αk+s(z)]=[αk+s(x),[D1,D2](y),αk+s(z)].

类似地，

[[D1,D2](x),αk+s(y),αk+s(z)]=[αk+s(x),αk+s(y),[D1,D2](z)].

所以[D1,D2]∈QC(T)，[QDer(T)，QCr(T)]∈QC(T).

(3)假设D1∈QCαk(T)，D2∈QCαs(T)，对任意的x,y,z∈T,有

[[D1,D2](x),αk+s(y),αk+s(z)]+[αk+s(x)，[D1,D2](y),αk+s(z)]+

[αk+s(x)αk+s(y),[D1,D2](z)]

=[D1D2(x),αk+s(y),αk+s(z)]-[D2D1(x),αk+s(y),αk+s(z)]+

[αk+s(x),D1D2(y),αk+s(z)]-[αk+s(x),D2D1(y),αk+s(z)]+

[αk+s(x),αk+s(y),D1D2](z)]-[αk+s(x),αk+s(y),D2D1](z)].

很容易得到

[D1D2(x)，αk+s(y),αk+s(z)]=[αk(D2(x))，D1αs(y)),αk+s(z)]=[αk+s(x),D2D1(y)，αk+s(z)].

[αk+s(x),αk+s(y),D1D2](z)]=[αs(D1(x))，αk+s(y),D2(αk(z))]=[D2D1(x),αk+s(y),αk+s(z)].

[αk+s(x),D1D2(y),αk+s(z)]=[αk+s(x),αk(D2(y))，D1(αs(z))]=[αk+s(x),αk+s(y),D2D1(z)].

(4)假设D∈Cαk,m(T)，则对任意的x,y,z∈T,有

δmD([x,y,z]=[D(x),αk(y),αk(z)]=[αk(x),D(y),αk(z)]=[αk(x),αk(y),D(z)],

因此

δm3D([x,y,z]=[D(x),αk(y),αk(z)]+[αk(x),D(y),αk(z)]+[αk(x),αk(y),D(z)],

且D′=3δmD∈End(T).所以这意味着D∈QDerαk,m(T).

(5)假设D1∈Cαk,m(T),D2∈Derαs,n(T)，对任意的x，y，z∈T，有

D1D2([x，y,z])

=δnD1([D2(x),αs(y)，αs(z)]+[αs(x)，D2(y),αs(z)]+[αs(x)，αs(y),D2(z)]

=δm+n[D1D2(x),αk+s(y),αk+s(z)]+δm+n[αk+s(x),D1D2(y),αk+s(z)]+

δm+n[αk+s(x),αk+s(y),D1D2(z)].

因此D1D2∈Derαk+s,m+n(T).

定理2.3令(T，[.，.，.]，α，δ)是保积Hom-δ李三系，α是满射且Z(T)是T的中心.则[C(T),QC(T)]⊆End(T,Z(T)).并且,若Z(T)={0},则[C(T),QC(T)]={0}.

证假设D1∈Cαk,m(T),D2∈QCαs(T)，对任意的x∈T，α是满射.对任意的y，z∈T，∃y′,z′∈T使得y=αk+s(y′),z=αk+s(z′),则

[[D1，D2](x)，y,z]

=[[D1，D2](x),αk+s(y′)，αk+s(z′)]

=[D1D2(x),αk+s(y′)，αk+s(z′)]-[D1D2(x),αk+s(y′)，αk+s(z′)]

=δmD1([D2(x),αs(y′)，αs(z′)])+[αs(D1(x)),D2(αk(y′))，αk+s(z′)]

=δmD1([D2(x),αs(y′)，αs(z′)])-δmD1([αs(x),D2(y′)，αs(z′)]

=δm(D1([D2(x),αs(y′)，αs(z′)])-[αs(x)，D2(y′)，αs(z′)])

=0.

因此[D1，D2](x)∈Z(T)和[D1，D2]∈End(T,Z(T)).并且,若Z(T)={0},则[C(T),QC(T)]={0}.

定义2.4令(T，[.，.，.]，α，δ)是char(F)≠2的域F土的保积Hom-δ李三系.则ZDer(T)=C(T)∩Der(T).

证假设D∈Cαk,m(T)∩Derαk,m(T).对任意的x,y,z∈T，有D([x,y,z])=δm[D(x),αk(y)，αk(z)]+δm[αk(x)，D(y),αk(z)]+δm[αk(x)，αk(y),D(z)].且

D([x,y,z])=δm[D(x),αk(y)，αk(z)]

=δm[αk(x)，D(y),αk(z)]

=δm[αk(x)，αk(y),D(z)].

则2D([x,y,z])=0，因为char(F)≠2，因此D([x,y,z])=0.

所以D∈ZDerαk(T)且C(T)∩Der(T)⊆ZDer(T).另一方面，假设D∈ZDerαk(T)，对任意的x,y,z∈T，有

D([x,y,z])=[D(x),αk(y)，αk(z)]=0.

容易验证D∈Cαk,m(T)∩Derαk,m(T)和ZDer(T)⊆C(T)∩Der(T).

定义2.5令(L，μ，α，δ)是Hom-δ-代数.L的Hom-δ-结合子是三线性映射asα:L×L×L→L定义如下asα=μ(μ⊗α-α⊗μ).

若作用在元素上，则映射asα的作用为

asα(x,y,z)=μ(μ(x,y),α(z))-μ(α(x),μ(y,z)),∀x,y,z∈L

令T是char(K)≠2的域K上的Hom-δ-代数带有双线性乘法ο.α：L→L是线性映射，则(L，ο，α,δ)是Hom-δ-代数.若下述恒等式成立：

xοy=yοx,

asα(xοy,α(z),α(ω))+asα(yοω,α(z),α(x))+asα(ωοx,α(z),α(y))=0,

对任意的x,y,z∈L.

性质2.6令(T，[.，.，.]，α，δ)是保积Hom-δ-李三系.带有运算D1·D2=D1D2+D2D1.则四元组(U，·，α,δ)是Hom-δ-代数.

推论2.7令(T，[.，.，.]，α，δ)是保积Hom-δ-李三系.带有运算D1·D2=D1D2+D2D1.则三元组(QC(T),·，α)是Hom-δ-代数.

证只需证明D1·D2∈QC(T)，对任意的D1∈QCαk(T)，D2∈QCαs(T)和x,y,z∈T，有

[D1·D2(x),αk+s(y)，αk+s(z)]

=[D1D2(x),αk+s(y)，αk+s(z)]+[D2D1(x),αk+s(y)，αk+s(z)]

=[D2(αk(x))，αs(D1(y))+αk+s(z)]+[D1(αs(x))，αk(D2(y))+αk+s(z)]

=[αk+s(x),D2D1(y),αk+s(z)]+[αk+s(x),D1D2(y),αk+s(z)]

=[αk+s(x),D1·D2(y),αk+s(z)].

类似地，

[D1·D2(x),αk+s(y)，αk+s(z)]=[αk+s(x)，αk+s(y),D1·D2(z)].

则D1·D2∈QCαk+s(T)和QC(T)是Hom-δ-代数.

定理2.8若(T，[.，.，.]，α，δ)是域(F)上保积Hom-李三系.

(1)若char(F)≠2，则QC(T)是Hom-δ李代数伴有运算[D1，D2]=D1D2-D2D1当且仅当QC(T)在这种运算下是Hom-结合代数.

(2)若char(F)≠3，α是满射且Z(T)={0}，则QC(T)是Hom-李代数当且仅当[QC(T)，QC(T)]=0.

证(1)(⟸)对任意的D1，D2∈QC(T),有D1D2∈QC(T)和D2D1∈QC(T)，因此[D1,D2]=D1D2-D2D1∈QC(T).所以，QC(T)是Hom-李代数.

(2)(⟸)明显.

(⟸)假设D1∈QCαk(T),D2∈QCαs(T),对任意的x,y,z∈T，存在y′,z′∈T,使得y=αk+s(y′),z=

αk+s(z′) .因为α是满射,QC(T)是Hom-李代数，因此[D1，D2]∈QCαk+s(T),则

[[D1，D2](x)，y,z]

=[[D1，D2](x),αk+s(y′)，αk+s(z′)]

=[αk+s(x)，[D1，D2](y′)，αk+s(z′)]

=[αk+s(x)，αk+s(y′),[D1，D2](z′)].

从引理2.2(3)的证明，有

[[D1，D2](x)，y,z]

=[[D1，D2](x),αk+s(y′)，αk+s(z′)]

=-[αk+s(x)，[D1，D2](y′)，αk+s(z′)]

=-[αk+s(x)，αk+s(y′),[D1，D2](z′)].

因此3[[D1，D2](x)，y,z]=0.由char(F)≠3，知[[D1，D2](x)，y,z]=0，即[D1，D2]=0.

3Hom-δ-李三系的拟导子

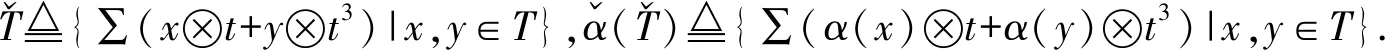
证对任意的x,y,z,u,v∈T和i,j，k,m,n∈{1,3},有

[x⊗ti,y⊗ti,z⊗tk]=[x,y,z]⊗ti+j+k

=-δ[y,x,z]⊗ti+j+k

=-δ[y⊗ti,x⊗ti,z⊗tk],

[x⊗ti,y⊗ti,z⊗tk]+[y⊗ti+z⊗tk,x⊗ti]+[z⊗tk+x⊗ti,y⊗tj]

=[x,y,z]⊗ti+j+k+[y,z,x]⊗ti+j+k+[z,x,y]⊗ti+j+k

=([x,y,z]+[y,z,x]+[z,x,y])⊗ti+j+k=0,

且

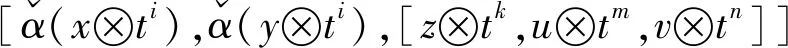
=[α(x⊗ti,α(y)⊗ti,[z⊗tk,u⊗tm,v⊗tn]]

=[α(x),α(y),[z,u,v]]⊗ti+j+k+m+n

=([[x,y,z],α(u),α(v)]+[α(z),[x,y,u],α(v)]+δ[α(z),α(u),[x,y,v]])⊗ti+j+k+m+n

为了方便，用xt(xt3)代替x⊗t(x⊗t3).

若U是T的子空间使得T=U⊕[T,T,T],则

φ(D)(at+ut3+bt3)=D(a)t+D′(b)t3,

这里D∈QDerak+s(T),D′在等式(1.2)中.a∈T,u∈U,b∈[T,T,T].

(1)φ是单射且φ(D)不依赖于D′的选取.

证(1)若φ(D1)=φ(D2)，则对任意的a∈T,b∈[T,T,T]和u∈U,有

φ(D1)(at+ut3+bt3)=φ(D2)(at+ut3+bt3)

即

因此D1(a)=D2(a).因此D1=D2和φ是单射.

对D∈QDerαk,m(T),假设存在D″使得

φ(D)(at+ut3+bt3)=D(a)t+D″(b)t3

和

[D(x),αk(y),αk(z)]+[αk(x),D(y),αk(z)]+[αk(x),αk(y),D(z)]=δmD″([x,y,z]).

则

D′([x,y,z])=D″([x,y,z]).

于是D′(b)=D″(b).因此

φ(D)((at+ut3+bt3)=D(a)t+D′(b)t3=D(a)t+D″(b)t3,

这意味着φ(D)由D决定.

对任意的x,y,z∈T，有

φ(D)([xt,yt,zt])=φ(D)([x,y,z])t3=D′([x,y,z])t3

=δm[D(x),αk(y),αk(z)]+[αk(x),D(y),αk(z)]+[αk(x),αk(y),D(z)])t3

=δm[D(x)t,αk(y)t,αk(z)t]+δm[αk(x)t,D(y)t,αk(z)t]+

δm[αk(x)t,αk(y)t,D(z)t]

现在定义映射f:Tt+Ut3+[T,T,T]t3→Tt3,

易知f是线性的.注意到

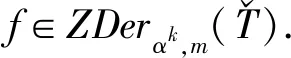
(g-f)(Tt)=g(Tt)-g(Tt)∩Tt3=g(Tt)-Tt3⊆Tt,(g-f)(Ut3)=0，

且

故存在D,D′在等式(1-1)中，使得对任意的a∈T,b∈[T,T,T],

(g-f)(at)=D(a)t,(g-t)(bt3)=D′(b)t3.

因此

δm[D(a1),αk(a2)t,αk(a3)t]+δm[αk(a1)t,D(a2),αk(a3)t]+

δm[αk(a1)t,αk(a2)t,D(a3)]=D′([a1,a2,a3])t3,

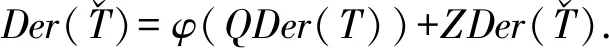
f(at+ut3+bt3)=φ(D)(at+ut3+bt3)=D(a)t+D′(b)t3.