风电场集中接入对集电线电流保护的影响研究

张军六， 张兴忠

（1.国网山西省电力公司 电力科学研究院， 山西 太原 030001； 2.太原理工大学， 山西 太原 030024）

0 引言

风电场集中接入电网后， 由于其复杂的短路电流特性和剧烈变化的运行方式， 会影响传统电流的保护性能。发生故障时，风机提供的短路电流包含特殊的暂态分量和序分量； 双馈型风机（Double Feed Induction Generator，DFIG） 的撬棒保护动作时， 风场内部的运行方式和短路电流分布会产生较大的变化。针对这些问题，传统的电流保护整定需要做出相应的改进， 从而满足应用要求[1]。 文献[2]分析了集电线路在接入接地变压器前后的零序电流变化及故障特征， 同时研究了零序电流保护在风电系统集电线路的应用。 文献[3]分析了直驱风机的短路电流特性和对选相元件的影响。 文献[4]提出了一种基于双曲正切函数动作特性的风电场集电线路反时限保护方法， 实现了风机箱变熔断器与集电线路保护之间的反时限动作特性配合。

风电机组由于区别于传统发电机， 故障时馈出的短路电流会对风场内部的集电线的正确动作造成影响。此外，DFIG 的撬棒保护动作情况，以及风场内部复杂多变的运行方式， 也给风电场集电线电流保护的整定带来了新的挑战。对此，本文以典型风电场为例，建立了DFIG 的短路计算模型，分析了传统电流保护整定计算模式在风电场集中接入时存在的问题， 并给出了相应的整定调整策略。 结合仿真，验证了这些调整策略的正确性。

1 DFIG短路电流特性

撬棒保护是DFIG 提高低电压穿越能力的主要措施， 撬棒保护的动作行为直接影响DFIG 的短路电流特性。 因此，DFIG 的故障特性研究应分别从考虑撬棒保护动作和计及励磁调节特性影响两个方面进行。

1.1 考虑撬棒电路动作的DFIG短路计算模型

在发生近区严重故障时， 撬棒保护动作，DFIG 定子电流中除含有稳态基频分量和衰减直流分量外， 还有角频率为ωr的转速频率电流分量。 在实际短路计算中，主要关心的则是基频分量[5]。 当发生故障时，文献[6]推导出了撬棒保护动作后DFIG 故障相电流正、 负序分量等效计算模型，等效电路如图1 所示。

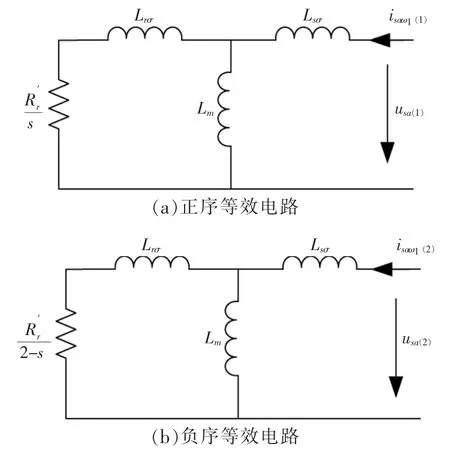
图1 撬棒保护动作后DFIG 故障相正负序等效电路Fig.1 Equivalent positive and negative sequence circuit of DFIG when its crowbar protections act

图中：s 为转差率；Lsσ为定子漏抗；Lrσ为转子漏抗；Lm为定转子互感；为转子绕组等效电阻。

从图1 可以看出，DFIG 稳态基频分量的等效计算模型实际上为异步电动机的等效模型。 撬棒保护动作瞬间，DFIG 对于电网而言由发电机变为电动机， 即由故障前的产生电流成为故障后的吸收电流。 对电流保护而言，它改变了电流流向，有可能会引起电流保护的工作异常。

1.2 计及励磁调节特性的DFIG短路计算模型

远区非严重故障情况下，DFIG 的转子绕组仍由变频器进行励磁。 此时，DFIG 定子绕组故障电流特性与传统同步发电机的故障电流特性相比存在较大的区别。 文献[7]通过研究DFIG 定子电力的故障特性， 指出定子绕组故障电流中只有衰减直流分量和强制基频分量， 而不含衰减的基频分量。 强制基频分量的大小则由电网电压跌落深度和低电压穿越运行期间所采用的控制策略共同决定。

目前，DFIG 在电网故障条件下的低电压穿越策略包括多种， 主要有平衡DFIG 总输出电流的控制策略[7]～[10]、恒定的DFIG 电磁转矩的控制策略[11]、恒定的DFIG 系统输出有功功率的控制策略[12]，[13]、恒定的 DFIG 发电系统无功功率的控制策略[14]，[15]。 本文将采用平衡的 DFIG 总输出电流控制策略[8]～[10]，[16]建立其短路计算模型。当 DFIG 的撬棒保护没有动作时， 在控制策略下，DFIG 等效为受控电流源模型， 仅向外部提供正序电流。DFIG 的正序等效电路如图2 所示。

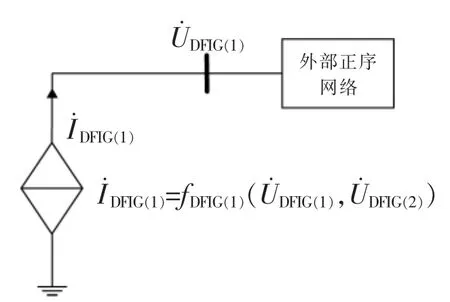
图2 DFIG 正序等效电路Fig.2 Equivalent positive sequence circuit of DFIG

2 传统集电线电流保护的整定方法

典型的双馈型风厂如图3 所示，单台DFIG的容量为1.5 MW， 风机通过箱式变压器升压至35 kV，再通过主变升压至110 kV，与外部电网相连。 风电场集电线电压等级为35 kV，线路不长，在电网侧配置有两段式电流保护（图中M 点）。

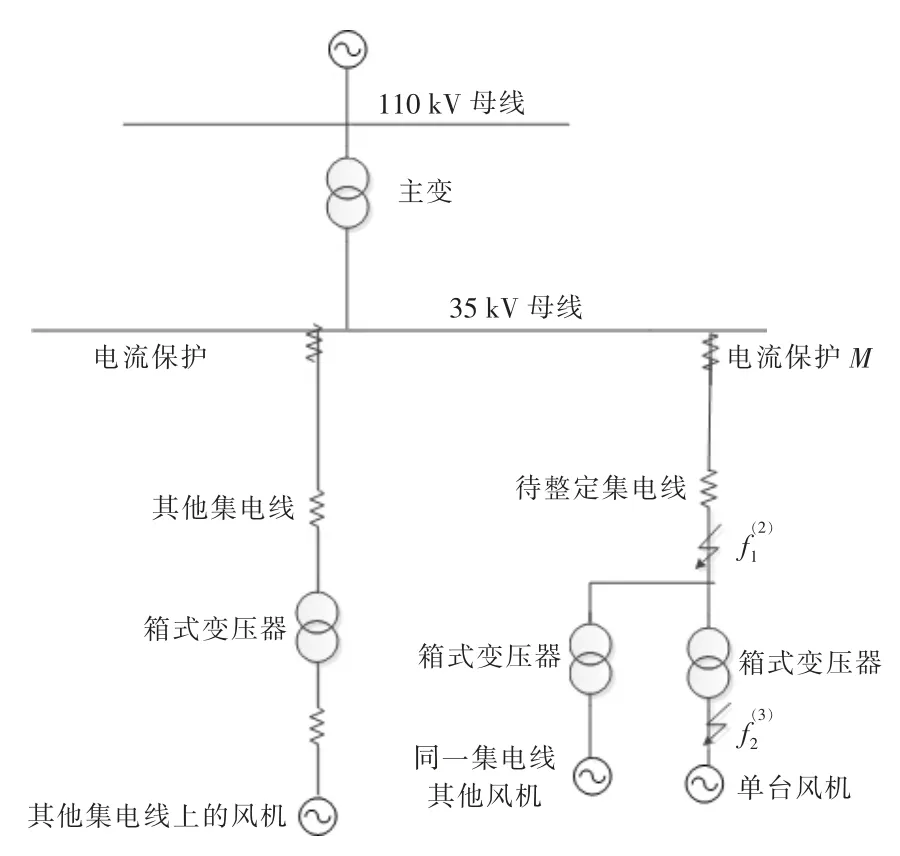
图3 典型的双馈型风厂示意图Fig.3 Diagram of typical wind farms

2.1 传统集电线电流保护Ⅰ段整定方法

在图3 中，当待整定集电线末端f1处发生故障时， 根据传统电流保护整定原则，M 点的电流保护Ⅰ段定值按保本线故障具有足够灵敏度整定。

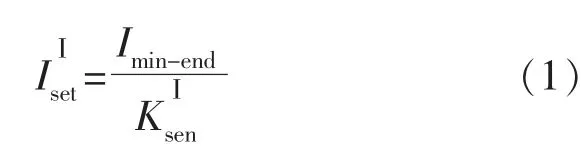
在计算Imin-end时， 传统整定方法采用的计算条件如下：图3 中f1处发生两相短路；系统采取最小运行方式；所有风电机组退出运行。

2.2 传统集电线电流保护Ⅱ段整定方法

在图3 中， 当待整定集电线的箱式变压器低压侧f2处发生故障时，根据传统电流保护整定原则，M 点的电流保护Ⅱ段定值按躲过集电线最近处箱式变压器低压侧最大短路电流整定。

在计算Imax时， 传统的整定方法采用的计算条件如下：图3 中f2处发生三相短路；系统采用最大运行方式；所有风电机组投入运行。

3 传统集电线电流保护整定方法存在的主要问题和调整策略

3.1 传统电流保护Ⅰ段整定方法存在的主要问题和调整策略

（1）电流保护Ⅰ段整定计算存在的主要问题

由式（1）可知，在电流保护Ⅰ段整定中，关键在于正确计算集电线末端最小短路电流Imin-end。传统的整定方法中，所有风机将退出运行，只考虑系统提供的短路电流。 这一整定方法的最大问题是没有考虑DFIG 的撬棒保护动作所导致的分流作用。因此，在计算待整定集电线上的最小短路电流时，应考虑其他集电线上风机的撬棒动作情况。

（2）电流保护Ⅰ段整定方法的调整策略

在DFIG 的撬棒保护不动作时， 风机为有源支路，故可采用传统整定方法计算Imin-end。 但当发生近区短路故障时， 可能导致风电机组撬棒保护动作，此时DFIG 励磁回路经撬棒电阻短接，失去励磁，其等值电路类似为异步电动机，会对系统的短路电流有分流作用， 导致流过待整定集电线上的短路电流减小，如图4 所示。

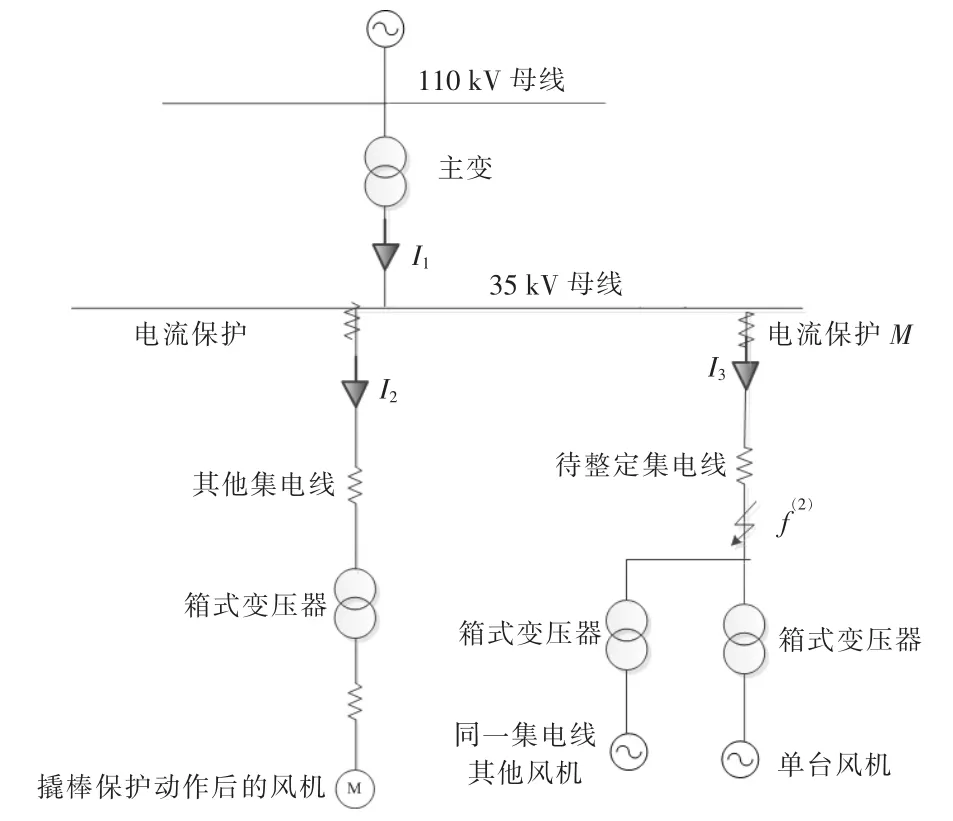
图4 电流保护Ⅰ段整定等效示意图Fig.4 Equivalent diagram of current protection I

在图4 中： 待整定集电线末端f 点发生两相短路；I1为系统侧向风场提供的短路电流；I2为DFIG 的撬棒保护动作导致的分流作用；I3为故障集电线上的短路电流。

根据以上分析，为了正确计算Imin-end，调整后的计算条件如下：集电线末端f 点发生两相短路；系统最小运行方式； 其他集电线上的DFIG 全部投入运行，并且撬棒保护动作。

3.2 传统电流保护Ⅱ段整定方法存在的主要问题和调整策略

（1）电流保护II 段整定计算存在的主要问题

由式（2）可知，在电流保护Ⅱ段整定中，关键在于正确计算流过待整定集电线的最大短路电流Imax。传统的整定计算方法在计算Imax时，将风机看作传统发电机的电压源串接内阻抗的等效电源，故计算条件为所有风机全部投入运行。 根据前述分析， 故障发生时，DFIG 的短路计算模型与传统发电机的等效模型有很大的不同： 若DFIG 的撬棒保护动作， 则DFIG 等效为异步电动机；若DFIG 的撬棒保护没有动作，则DFIG 等效为受控电流源模型，向外提供短路电流。 此时，其他集电线上的风机会向待整定集电线上输出短路电流。故传统的整定方法的计算条件不一定适用于风电场集中时集电线电流保护Ⅱ段的整定。

（2）电流保护Ⅱ段整定方法的调整策略

由式（2）可以看出，箱式变低压侧的最大短路电流与电网的运行方式、 其他集电线的风机运行方式和本集电线上其他风机的运行方式有关。 每一个条件的变动， 均会影响待整定集电线的最大短路电流。 下面以图5 所示的电流保护Ⅱ段整定等效示意图为例，详细分析电网不同计算条件对短路电流Imax的影响。

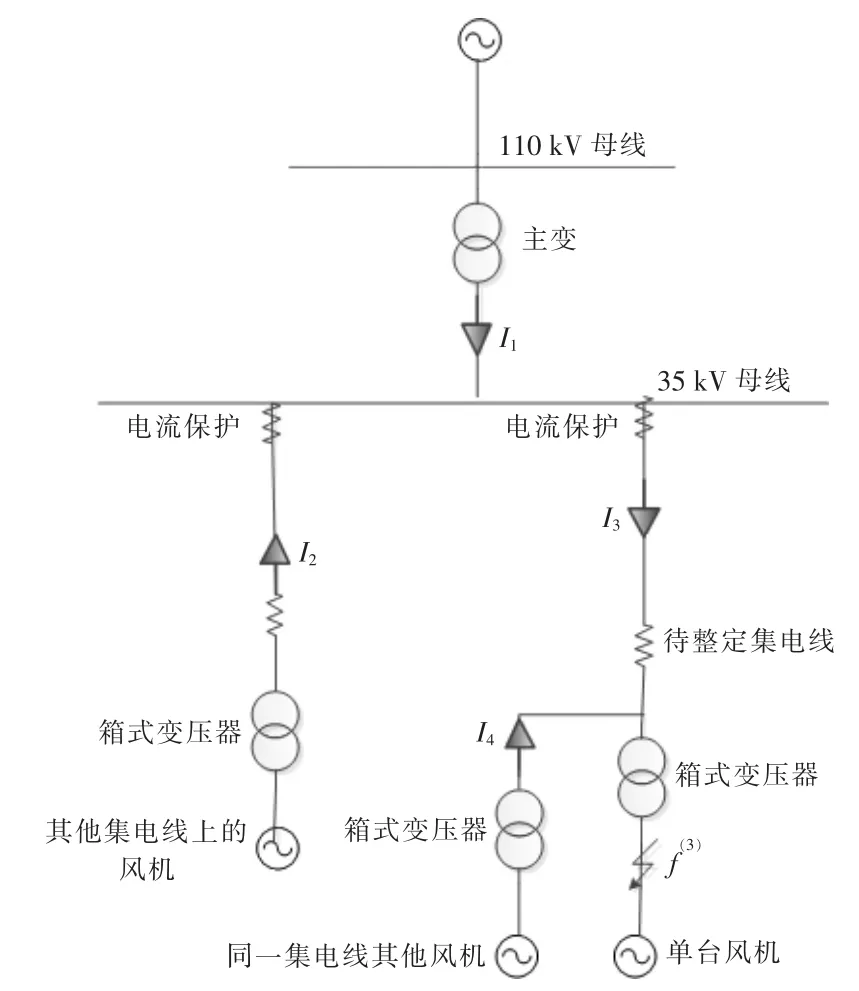
图5 电流保护Ⅱ段整定等效示意图Fig.5 Equivalent diagram of current protection II

在图5 中， 待整定集电线箱变低压侧f 点发生三相短路故障，I1为系统侧向风场提供的短路电流，I2为其他集电线风电机组提供的短路电流，I3为故障集电线上的短路电流，I4为待整定集电线上其他DFIG 提供的短路电流。

计算Imax也即计算I3的最大值。 由图5 可知，I3主要受 I4，I2和 I1影响。其中：I4由待整定集电线其他并联风电机组的运行方式决定；I2由其他集电线风电机组的运行方式决定；I1由外部系统的运行方式决定。下面分别对这三个方面进行分析。

①待整定集电线其他并联风电机组的运行方式

在传统的整定方法中，待整定集电线上并联的其他风电机组的运行方式为全部投入运行。 考虑到DFIG 的撬棒保护动作情况后，这些DFIG 可以等效为异步电动机， 此时DFIG 由提供短路电流转变为吸收短路电流， 从而减小短路阻抗并增大I3。 故传统整定方法中待整定集电线上其他并联风电机组的运行方式应将DFIG 的撬棒保护设置为动作动态。

②其他集电线风电机组的运行方式

在传统的整定方法中， 其他集电线上的风电机组的运行方式为全部投入运行， 此时其他集电线上的风机提供的短路电流I2最大，同时也增大了I3。 故传统整定方法中其他集电线风电机组的运行方式不需要作调整。

③外部系统运行方式

对图5 使用叠加定理，得到图6。

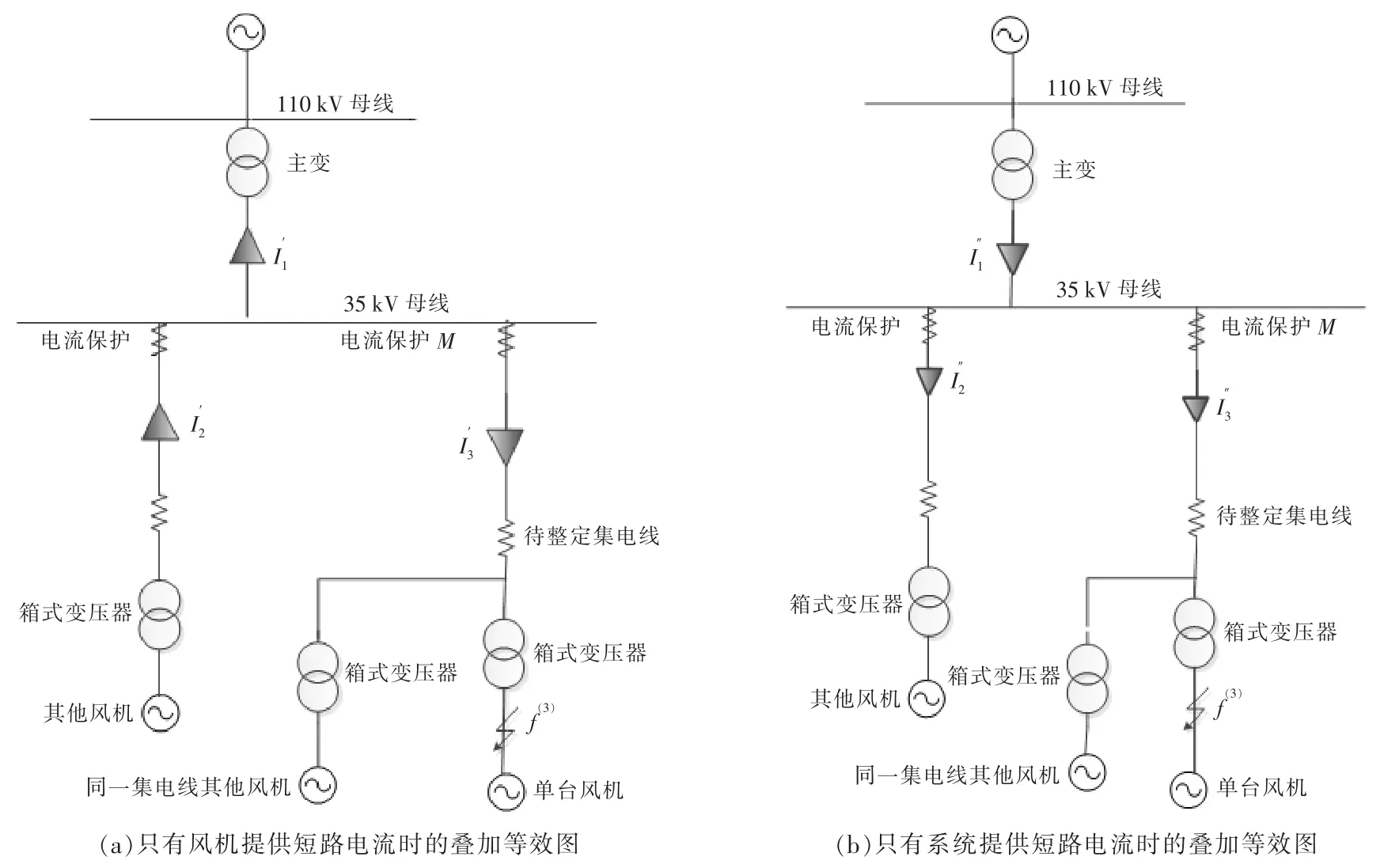
图6 考虑系统运行方式时的叠加等效图Fig.6 Equivalent diagram when considering the operation mode of power system

在图6 中，根据叠加定理有：

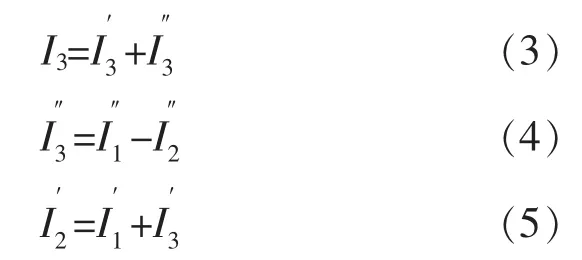
由式（3）可以看出，I3由两部分组成，当同时最大时，I3最大。

根据以上对三个影响因素的分析， 集电线电流保护Ⅱ段整定方法如下： 集电线箱变低压侧发生三相短路； 待整定集电线上其他并联的DFIG的撬棒保护动作； 其他集电线上的风电机组全部投入运行； 系统运行方式的选取须考虑系统强弱和风电场容量两个方面。

4 仿真分析

为了验证对集电线传统电流保护的分析和调整策略的正确性，以PSCAD/EMTDC 为仿真平台，构建如图3 所示的典型风电场的仿真模型。 系统参数设置： 基准电压为110 kV， 基准容量为100 MV·A；最大运行方式下，正序阻抗为0.169 3 p.u.，零序阻抗为0.328 6 p.u.；最小运行方式下，正序阻抗为 0.175 p.u.，零序阻抗为 0.355 p.u.。 风电场参数设置：单台风机额定容量为1.5 MW，单台箱式变压器的额定容量为1 600 kV·A， 变比为0.69/36.75 kV，联结组别为Yd，漏电抗为6.44%；主变额定容量为100 000 kV·A，变比为36.75/115 kV，联结组别为YY，漏电抗为10.6%；待整定集电线阻抗为0.243 p.u.。

4.1 集电线电流保护Ⅰ段仿真验证

在构建的仿真模型中， 在待整定集电线末端f 点发生AB 两相短路时，分别对以下两种整定方法进行仿真分析，Imin-end仿真结果如表1 所示。 表中△为按照调整后的整定方法得到的Imin-end相比于传统整定方法的Imin-end的变化率。

①传统整定方法：系统最小运行方式，所有风机退出运行。

②调整后的整定方法： 系统最小运行方式，DFIG 投入运行且撬棒保护动作。

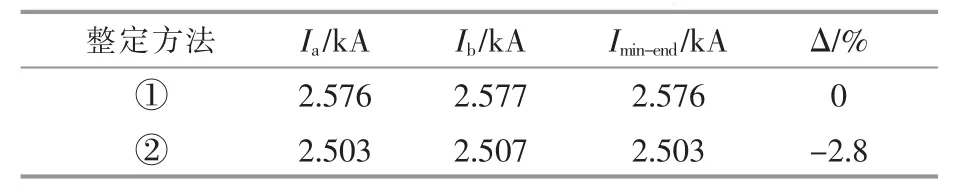
表1 电流保护I 段仿真结果Table 1 Simulation results of current protection I

表1 的仿真结果表明， 通过调整后的整定方法得到的Imin-end相比于传统方法得到的Imin-end减小了2.8%，减小的幅度不大。 故集电线电流保护Ⅰ段整定可以忽略风电机组的影响， 按传统整定方法计算。

4.2 集电线电流保护II段仿真验证

在构建的仿真模型中， 当待整定集电线箱式变压器低压侧f 点发生三相短路时， 分别对以下5 种整定方法进行仿真，Imax仿真结果如表2 所示。 表中△为按照调整后的方法得到的Imax相比于传统整定方法的Imax的变化率。

①传统整定方法：系统最大运行方式，所有风机投入运行。

②调整后的整定方法1：系统最大运行方式，待整定集电线上其他并联的DFIG 的撬棒保护动作，其他集电线上的风机全部退出运行。

③调整后的整定方法2：系统最小运行方式，待整定集电线上其他并联的DFIG 的撬棒保护动作，其他集电线上的风机全部退出运行。

④调整后的整定方法3：系统最大运行方式，待整定集电线上其他并联的DFIG 的撬棒保护动作，其他集电线上的风机全部投入运行。

⑤调整后的整定方法4：系统最小运行方式，待整定集电线上其他并联的DFIG 的撬棒保护动作，其他集电线上的风机全部投入运行。

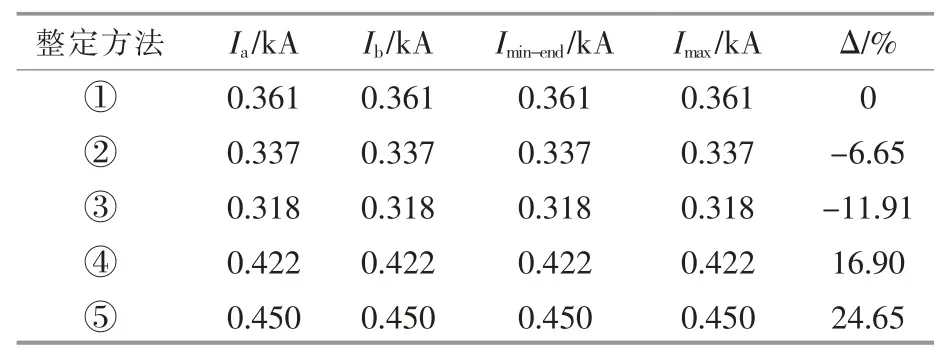
表2 电流保护II 段仿真结果Table 2 Simulation results of current protection II

表2 的仿真结果表明： 调整后的整定方法②和③相比于①，Imax减小了。 这两种整定方法中将其他集电线上的风机退出了运行， 这也证明了为了得到更大的Imax，需要将其他集电线上的风机全部投入运行； 整定方法④相比于①，Imax增大了16.9%，说明待整定集电线上的DFIG 的撬棒动作对减小短路阻抗的作用十分明显， 证明了前述理论分析的正确性； 整定方法⑤相比于①，Imax增大了24.65%，与方法④相比，增幅更大。说明在其他条件相同的情况下， 系统选择最小运行方式时的Imax要大于系统选择最大运行方式时的Imax， 而且系统运行方式的选择应综合考虑系统强弱和风电场容量两个因素的影响。 在对集电线电流保护Ⅱ段进行整定时，对于弱系统、大容量风场的电网结构，系统运行方式应选择最小运行方式；对于强系统、小容量风场的电网结构，系统运行方式应选择最大运行方式。

5 结论

双馈风电机组复杂的故障电流特性对风电场集电线电流保护有重要影响， 将严重影响风电场和电网的安全稳定运行。 基于此， 本文分析了DFIG 的故障电流特性， 建立了相应的计算模型。分析了风电场集电线传统电流保护存在的缺陷，提出了适用于DFIG 集电线的电流保护整定新方案。 得出以下结论。

①撬棒保护对DFIG 故障电流有重要影响，传统同步发电机的次暂态电势串接次暂态阻抗模型已不适用，需要建立考虑撬棒保护动作的DFIG模型和计及励磁调节特性影响的DFIG 模型。

②适用DFIG 集电线电流保护与传统电流保护整定原则有较大区别， 与系统的运行方式和风场内部的运行方式等因素有关。 在电流保护I 段进行整定计算时， 需要将DFIG 的撬棒保护设为动作状态。 而在电流保护II 段整定计算时，系统运行方式的选择要考虑系统强弱和风场容量等因素的影响， 待整定集电线上其他并联的DFIG 的撬棒保护应设定为动作状态， 其他集电线上的风机应全部投入运行。

③仿真结果证明了调整后的集电线电流保护整定方法的正确性。 调整后的整定方法提高了风电场继电保护性能， 对电网和风电场的安全稳定运行有重大帮助。