关于排污水管的优化设计模型
2020-05-18马君儿李东明
马君儿 李东明


【摘要】为了响应“五水共治”决策,多地都在重新铺设排污水管道,以达到排污整治的效果。本文前两个小题是一个非线性规划(NLP)的优化模型,通过寻找线路(折线段形式)的最优转折点位置,借助微积分、几何学知识,及Matlab软件的调用,得到污水管的最优布置方案和造价总费用的最小值。并且利用求多元函数的极值方法,得到污水处理池造价最低时的设计尺寸与污水池造价的最小值。
【关键词】管线布置 造价 最优 距离
一、问题的提出
青山绿水就是金山银山。水是生命之源,水与浙江有着渊源:由于浙江省内分布着钱塘江、瓯江、苕溪、甬江、灵江、飞云江、鳌江等七大河流,因此水也是浙江之源。浙江作为沿海发达地区,随着经济的迅猛发展,水环境正在承受着越来越大的压力。为了保护生态环境,防止河流被工业污水、生活污水等污染,浙江省委十三届四次全会,提出了“治污水、防洪水、排涝水、保供水、抓节水”的“五水共治”决策。其目的要求,是要以“五水共治”为契机,让水与人更好地和谐相处。“治污水”作为“五水共治”的首要任务,主要是通过污水处理, 整治垃圾河、黑河、臭河里的水,让其水质基本达到无毒无害、不黑不臭,让水可用于农田灌溉,让人可在河中游泳。
具体问题如下
(1)假设浙江省某城镇有甲(位于点A)、乙(位于点B)两工厂,都处于线段CD同侧,A离线段CD的距离为a,垂足为C,B离线段CD的距离为b,垂足为D,CD的间距离为,现准备在线段CD上取点E,造一个容积为K的无盖长方体的污水处理池。假设:从甲、乙两厂至点E间铺设的污水管单位造价(万元/千米)一致,问:E点选在何处,使得铺设排污水管的总造价最低?
(2)假设甲、乙两厂的具体位置由图1所示,其中B位于城区(图中的II区域),A位于郊区(图中的I区域),城区与郊区两个区域的分界线用图中的虚线表示。图中各字母表示的距离(单位:千米)分别为a=5,b=8,c=15,l=20。若所有管线的铺设费用均为每千米0.72万元。但铺设在城区的管线还需增加附属物的拆迁补偿等附加费用,设附加费用为0.2(万元/千米),请给出排污管线的布置方案及相应的费用?
(3)对于问题一与问题二中,如果还准备在点E处造一个容积为V的无盖长方体的污水处理池,假设池底与四个侧面的单位造价(万元/平方米)相同,问:应如何选择污水处理池的尺寸,方可使污水处理池的总造价最低?
二、模型的假设
①两个工厂及所有排污管线均在线段的同一侧。②忽略地域、地貌等对污水管铺设上的影响,非共用管线与共用管线均以直线段铺设。③当城区考虑附加费用时,假设污水处理池选址在郊区。④假设污水处理池选址位于甲、乙两厂所铺设的管线的交点M在CD线段上的投影点。⑤假设每支段上的管线单位造价(万元/千米)相同。⑥假设污水处理池是容积为V无盖的长方体,且池底与四个侧面的单位造价(万元/平方米)相同。
三、符号的说明
α: a:甲厂到CD的垂直距离;b:乙厂到CD的垂直距离;1:CD间的直线段长度;M:甲厂、乙厂污水管线的交点;E: 污水处理池的选址;k:附加费用(万元/千米);F: 乙厂的污水管线同郊区和城区的分界线的交点;q1:铺设甲厂污水的管线单位造价(万元/千米);
q2铺设乙厂污水的管线单位造价(万元/千米)(不考虑附加费用);q3铺设两厂共用管线的单位造价(万元/千米);Q:污水管线铺设的总费用;q:污水处理池侧面与池底的造价(万元/平方米);Z: 污水处理池的总造价。
四、模型的建立与求解
问题一:模型的建立与求解
建立以C为原点,CD所在的直线为x轴,CA所在的直线为 y轴的直角坐标系,则各点坐标为A(0,α),B(l,b),C(0,0),D(l,0),设M为(x,y),则建污水处理池处点E为(x,0)。
问题二:模型的建立与求解
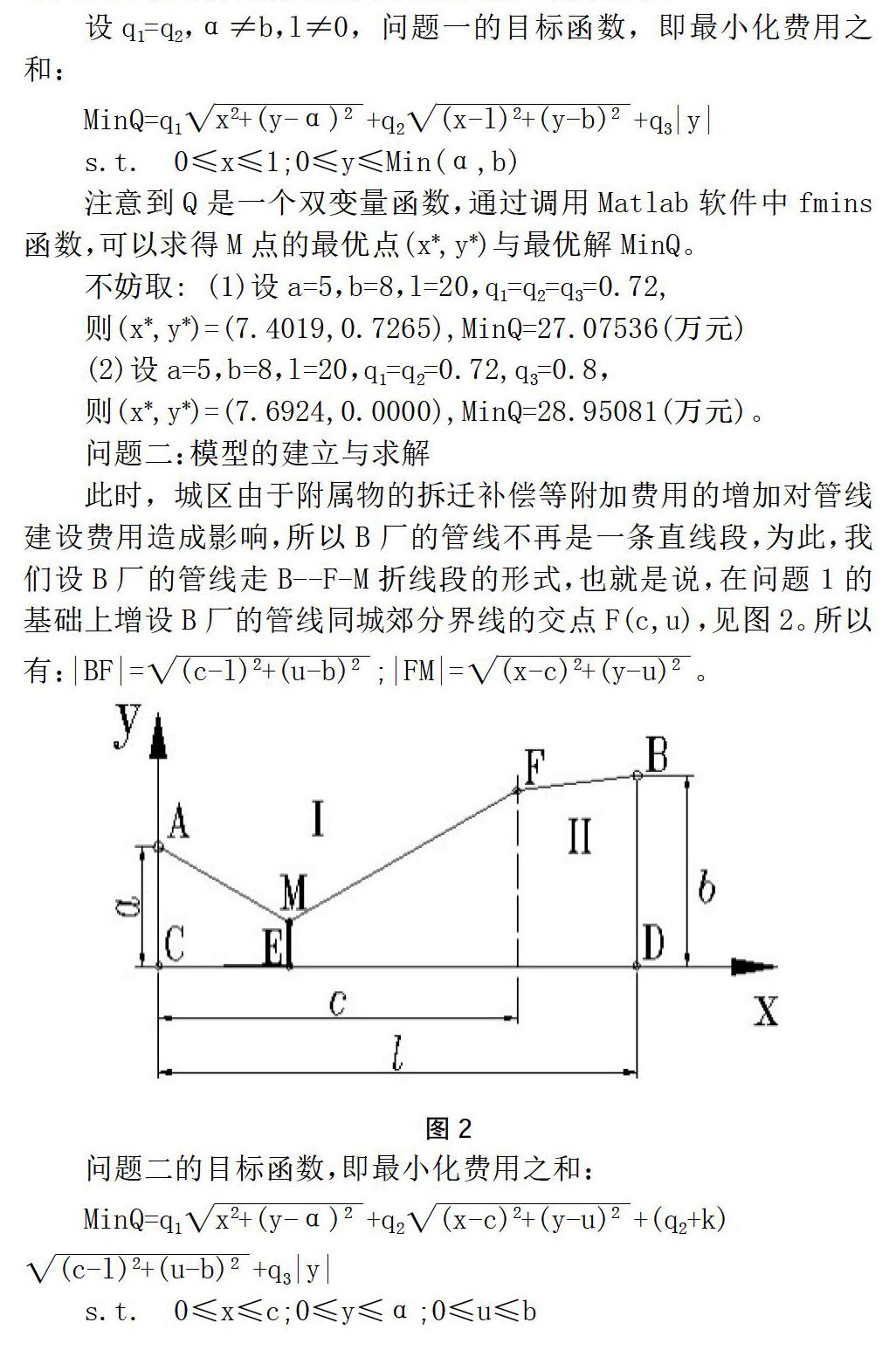
此时,城区由于附属物的拆迁补偿等附加费用的增加对管线建设费用造成影响,所以B厂的管线不再是一条直线段,为此,我们设B厂的管线走B--F-M折线段的形式,也就是说,在问题1的基础上增设B厂的管线同城郊分界线的交点F(c,u),见图2。所以有:|BF|=;|FM|=。
问题三:模型的建立与求解
设污水处理池是无盖的长方体,且池底与四个侧面的单位造价相同:为q(万元/平方米)。设污水处理池池底的长为x,宽为y,则由长方体的体积公式,可求得:高为V/(xy),记:对应的表面积为S,总造价为Z。根据假设,则Z=q*S。其中:单位造价q(万元/平方米)为定值,因此,只要求出表面积S的最小值就行。
事实上,表面积:s=x·y+2v(+)(x>0,y>0),则偏导数=y-,=y-。令=0且=0,得驻点(底面边长):x0=y0=,这时高h0=。因为表面积S的最小值必定存在,且开区域内驻点唯一,所以,总造价的最小值就在该驻点处取得,即当污水处理池的池底长与宽都为,高为时,总造价达到最小值:Z0=3q。
五、模型的评价
(1)问题一与问题二中,都假设:甲、乙两厂的生产规模基本相同。因此支流上的排污水管单位造价(万元/千米)不妨假设相等。如果甲、乙两厂的生产规模相差较大,意味着:支流的污水管应有粗细,即:支流上的排污水管单位造价(万元/千米)q1与q2应假设为:不相等。
(2)问题二中,關于“铺设在城区的管线还需增加附属物的拆迁补偿等附加费用”,应根据不同城市、不同区域来综合评估得到相应的附加费用。
(3)问题三中,假设污水处理池是容积为V无盖的长方体,且侧面与池底的单位造价(万元/平方米)相同。可以推广为:池底的单位造价/侧面的单位造价为p(p>1)。再利用多元函数的极值计算,推导出对应的最优设计尺寸及最低总造价。
(4)如果是整治农村某个自然村人们的生活污水,则应根据住房分布情况(如果整村分布范围较广,呈若干个片区相对集中分布),则应“分片分组布置污水管线,多建几个小污水处理池”。这样设计,总造价相对而言会比“集中造一个大污水处理池”要经济实用。
六、模型的应用
现状分析:随着政府在城市建设中人力与物力的不断投入,中国城市的污水处理率已提前完成给定的目标,相对而言,县城和建制镇的污水处理率依然不理想。特别是农村,一些小型企业私自排放工业污水,或不规范办理养猪场,乱排污秽物,导致地下水、流域支流、河网的水质持续恶化,河中的鱼越来越少,甚至有些河段水体发黑发臭,直接影响人们的生活质量与生活环境。如果不及时采取有效措施,污染将持续扩大。准对现状,从上至下,各级部门应统一思想,创造条件,投入资金,重点在小城镇和规模较大的村庄,铺设排污水管道、建设污水处理设施,进行污水处理,从而改善河道水质。相信通过政府、企事业、个人,大家的齐心协力,真正搞好“五水共治” 这项惠民工程,那么,蓝天白云下,鱼儿在清彻见底的溪涧畅游,一幅幅美景将随处可见。
参考文献:
[1]王家文,曹宇.MATLAB 6.5图形图像处理[M].北京:国防工业出版社,2004.
[2]姜启源.数学建模[M].北京:高等教育出版社,1993.
[3]同济大学数学系编.高等数学(上、下册)(第七版)[M].北京:高等教育出版社,2014.
[4]同济大学数学系编.高等数学习题全解指南(上、下册)(第六版)[M].北京:高等教育出版社,2010.
作者简介:马君儿(1965-),女,职称:副教授,主要从事高等数学教学;李东明(1963-),男,职称:中学高级,主要从事中学数学教学。
