基于SEM赋权与灰色关联理论的深基坑支护方案优选①

洪文霞， 李蓓蓓， 张利源, 鹿 乘

(青岛理工大学管理工程学院，山东 青岛 266520)

0 引 言

随着社会发展及城市化进程加快，高层建筑崛地而起，隧道、地铁等地下工程的不断开发，对深基坑支护方案的选择变得尤为重要，它关系到整个工程的成败。影响深基坑支护方案优选的因素繁多，且因素间关联关系复杂，带有不确定风险性及灰色关联性。研究者曾对基坑支护方案安全性进行评价[1],一些学者运用灰色Euclid理论[2]、集对分析法[3]、网络分析法[4]、德尔菲和优序图法[5]对方案进行优选，这些方法带有各自局限性，如集对分析方法忽略了优选指标的权重的科学确定，且诸多方法中鲜有验证基坑方案优选指标体系结构效度，因此，有必要对方案优选指标体系合理性进行验证。基于此，本文首先运用结构方程模型验证优选指标体系的合理有效性并定量确定指标权重，再运用灰色关联理论进行方案优选，以提高方案优选的合理性，使方案决策结果更具有说服力。

1 深基坑支护方案优选评价指标体系

科学、全面、合理的方案优选评价指标体系的构建是准确决策方案的基础。深基坑支护方案的影响因素众多，本文在相关文献[6-8]研究的基础上，结合本基坑工程的实际特点、工程地质、水文地质等自然条件，遵循全面客观性、科学可行性原则，从技术可行性、经济型、施工可操控性、环境影响四方面构建方案优选指标体系，如下图1所示。再运用结构方程模型定量验证该指标体系的结构效度并定量确定指标权重。

2 基于SEM与灰色关联理论优选模型的构建

2.1 基于SEM的方案优选评价指标赋权

结构方程模型(SEM)是一种强大的多元统计方法，此法分析的基础是变量协方差矩阵。SEM包括测量模型和结构模型两部分，既能对路径分析，也能对因子分析[9]。且结构方程模型是一种验证性方法，通过实际收集的问卷数据来验证假设模型。

2.1.1 问卷设计与数据收集

基于上述构建的优选评价指标体系，对指标影响方案选择的重要性水平进行问卷调查。根据指标重要程度差异，采用李克特七级量表编制，问卷第一部分是被测者的基础信息，第二部分是14个方案评价优选指标的题项和回答。向基坑工程相关领域专家、学者和项目有工作经验人员发放问卷，回收问卷后对实际样本数据进行处理。

2.1.2 结构方程模型建立与拟合

SEM中因子路径荷载代表的是因子间关系密切程度。因子荷载越大，表明该变量的影响地位高，影响力大。基于方案优选评价指标体系作出如下假设，并在AMOS 23.0软件中建立假设模型：

H1:环境影响因素对方案优选有显著正向作用；

H2:总造价因素对方案优选有显著正向作用；

H3:施工可操作性对方案优选有显著正向作用；

H4:方案技术可行性对方案优选有显著正向作用；

图1 深基坑支护方案优选评价指标体系

2.1.3 模型拟合

初始模型拟合程度的检验在AMOS 23.0软件中完成，本文采用的拟合指标有χ2/df,RMSEA,GFI,AGFI,NFI,CFI[8]等，拟合指标能直接反映模型拟合程度。

2.1.4 确定权重

通过上一小节得到的各因子的标准化因子负荷量确定各级指标权重。公式(1)如下:

(1)

其中βi表示各级指标权重，Li表示SEM中各级因子负荷量，即路径系数。

2.2 基于灰色关联理论方案优选模型构建

通过客观曲线形状的相似性对序列间关联程度作出判断是灰色关联理论的核心思想。图形间越相似，灰色关联度越大；反之，则关联度越小。

2.2.1 原始数据变换

为了解决不同数据间衡量单位差异的问题，需要对原始数据进行无量化处理，达到统一量纲的目的。对数据统一量纲的两种主要方式有：

初值化变化：

(2)

均值化变换：

(3)

2.2.2 计算关联系数

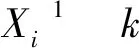
(4)

找出|Δij(k)|的最小值Δmin和最大值Δmax。关联系数ξij(k)：

(5)

其中η∈[0,1],通常取0.5。

2.2.3 计算各序列Xj的综合关联度γi

(6)

根据综合关联度排序，关联度值最大的为优选方案。

3 应用实例

以青岛地铁1号线某在建站深基坑为例，该地区地形平坦，因靠近海域，基坑水位较高，土质较粘稠。在考虑基坑特征、地质条件、经济性等问题，并结合专家讨论意见，提出三种备选初步支护方案：方案1：地下连续墙+内支撑支护；方案2：旋喷桩+钻孔灌注桩+锚杆支护；方案3：旋喷桩+钢管桩灌浆。

3.1 确定优选评价指标权重

3.1.1 数据收集与检验

问卷设计采用李克特7级量表法，1-7分别表示重要程度从低到高。问卷调查对象为深基坑专业相关人员。问卷调研周期为2019年10月-12月，最初收回问卷共230份，其中有效问卷204份。利用SPSS 25.0软件分析数据，得出Cronbach’s Alpha结果为0.89，表明问卷整体数据有较高可信度，继续下一步研究。再对数据进行KMO( Kaiser- Meyer- Olkin)检验，如下表1。检验结果显示KMO=0.882，球体检验的P=0显著，说明问卷结构效度良好，可继续进行因子分析。

表1 KMO与巴特利特检验

3.1.2 模型建立与拟合

数据通过克隆巴赫和KMO检验后，即可导入AMOS 23.0软件模型中进行拟合，运算结果，如图2所示。拟合指数，如表2所示。由表2可知，各拟合指标均符合标准要求；由图2知，各级因子载荷均大于0.6，影响程度较大，模型拟合度较好。说明2.1.2中假设成立，且验证了方案优选指标体系的建立恰当合理。

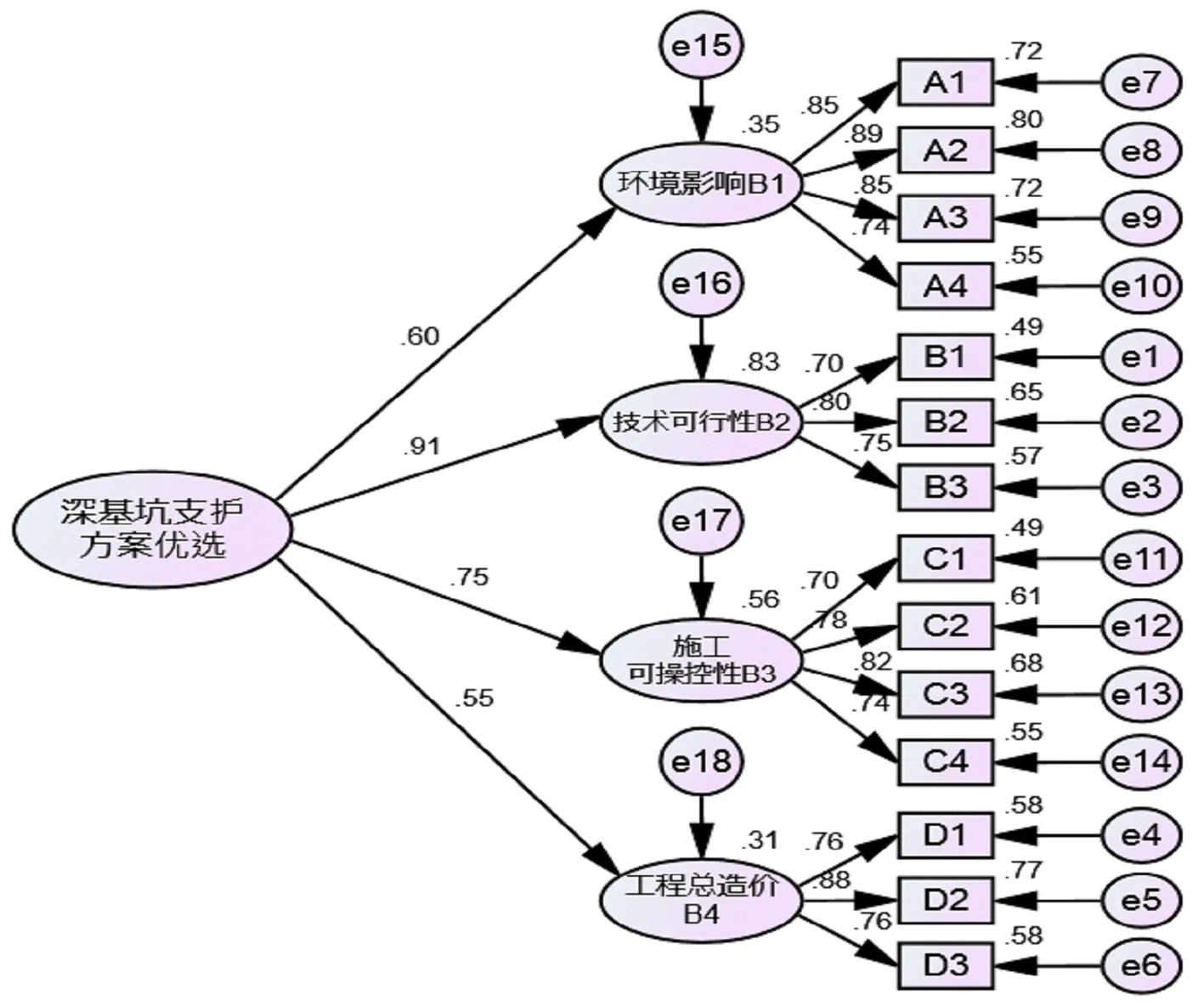
图2 深基坑支护方案优选评价体系验证模型

表2 SEM模型整体适配度指标检验

拟合指数χ2/dfRMSEASRMRGFIAGFINFICFI标准临界值<3<0.1<0.08>0.9>0.8>0.9>0.9检验结果1.6550.0570.060.9260.8930.9240.968

3.1.3 权重确定

根据图2中，对于4个潜变量的一级指标，分别计算各自路径系数Li占4个潜变量路径系数总和的比重，即为权重。同样方式，可以计算14个观测变量二级指标权重，即利用公式(1)计算各个变量指标权重，如下表3所示。

表3 方案优选指标权重

3.2 基于灰色关联理论最优方案选择

首先，走访调研了8名相关领域专家，根据各自工程经验，以第一章构建的方案优选指标为标准，对待选方案与理想方案A0的各指标作出评语评价，进而确定各个方案的期望值。然后，通过计算分析各方案综合关联度的大小，选择最优方案。其中，B2,B3,C5,C6,C7,C9属效益型指标，越大越好；B1,B4,C1,C2,C3,C4,C8,C10,C11,C12,C13,C14属成本型指标，越低越优。专家评语平均原始数据，如表4所示。

表4 专家对备选方案和理想方案各指标评价(一、二级指标)

3.2.1 依据一级指标确定方案

以一级指标为计算参照，对B1-B4原始数据按公式(3)进行均值变换，如表5所示。按照式(4)、式(5)、式(6)计算综合关联度系数矩阵、整体综合关联度，由于篇幅原因，得最终方案综合关联度分别为γ1=0.57，γ2=0.782，γ3=0.566。

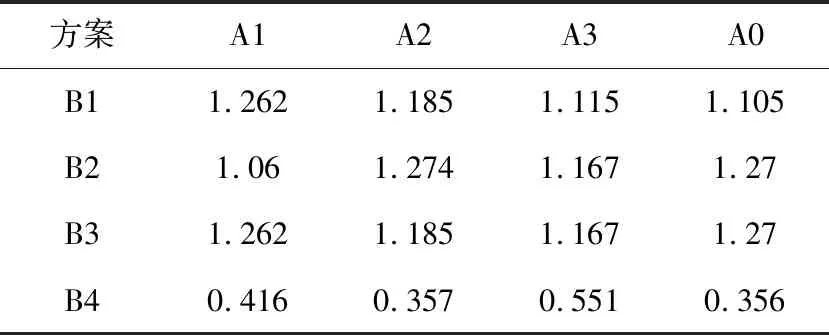
表5 一级指标均值化变换矩阵

将一级指标综合关联度排序可知γ2>γ1>γ3，根据最大最优原则，可确定A2为最优支护方案。

3.2.2 依据二级指标确定方案

以二级指标为参数，对C1-C14原始数据按公式(3)进行均值变换，如表6所示。按照式(4)、式(5)、式(6)计算综合关联度系数矩阵、整体综合关联度，同样可得最终方案综合关联度分别为γ1=2.945，γ2=3.11，γ3=3.029。

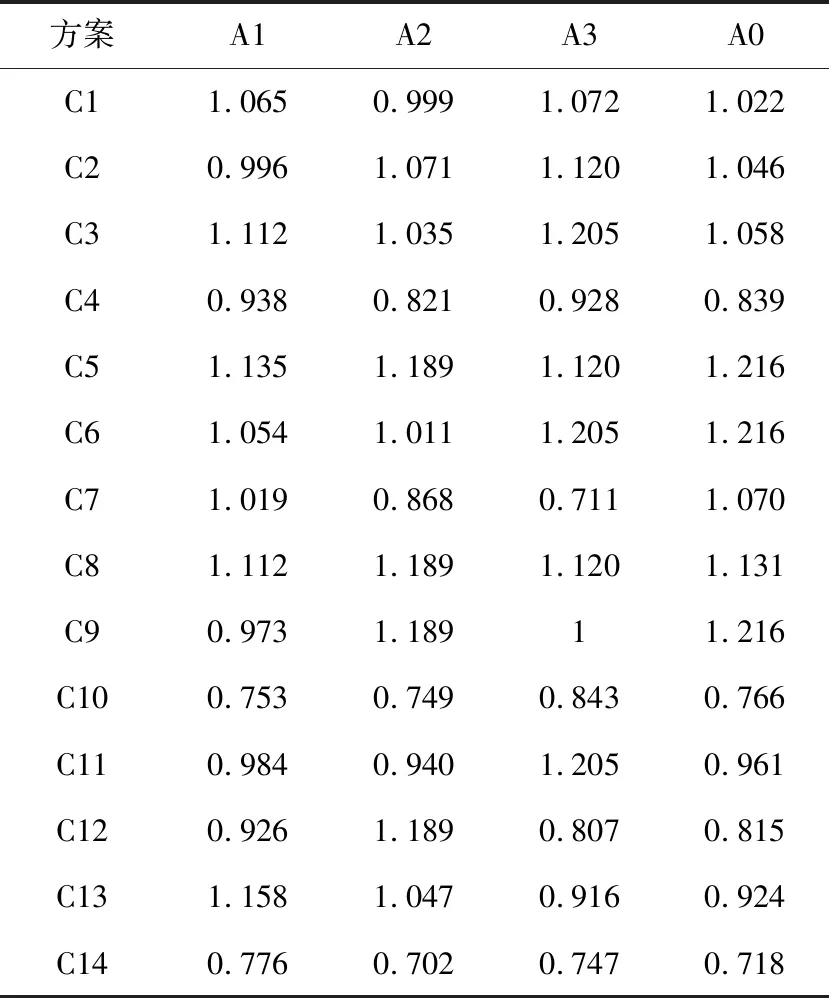
表6 二级指标均值化变换矩阵

同理，将二级指标综合关联度排序可知γ2>γ3>γ1，选择综合关联度最大的A2为最优支护方案。

综上两种方式优选方案的结果均为A2方案最优，因此，方案2：旋喷桩+钻孔灌注桩+锚杆支护将作为该地铁站基坑支护优先选择方案。该选择与实际工程的选择不谋而合，且方案实施效果较佳，展现了该方案优选模型的显著效果，验证了其切实可行性。

4 结 论

深基坑支护方案优选是基坑工程重要的基础工作。

1)传统深基坑优选方案模型在指标权重确定方面主观性较强，本文利用结构方程模型对方案优选的调查问卷数据进行分析，在检验深基坑支护方案优选指标体系结构效度的同时，定量确定了指标权重，权重确定更科学。

2)以青岛市1号线某站点工程为依托，结合工程实际情况，较为全面地构建了深基坑支护方案优选评价指标体系，包括4个一级指标，11个二级指标。

3)基于SEM赋权与灰色关联理论模型，分别以一级、二级指标为计算依据，两种计算方式相互证明，且计算结果与实际工程一致，表明该方法的科学合理性，为深基坑支护方案优选提供新的选择。