基于灰色关联和PSO–SVM的葡萄霜霉病的短期预测

吴宁，陈天恩，姜舒文，张驰，鲁梦瑶，张玮

(1.上海海洋大学信息学院，上海 201306；2.国家农业信息化工程技术研究中心，北京 100097；3.北京市农林科学院植物保护环境保护研究所，北京 100097)

葡萄霜霉病极易导致果穗无法正常生长，引发减产，造成严重的经济损失[1]。快速、准确地作出预测预报是有效防治和控制葡萄霜霉病发生、发展的重要手段，对保证葡萄高产、安全和优质生产具有重要意义。

预测葡萄霜霉病的常规方法主要有经验模型、系统模拟法、回归统计法等[2–3]。MENESATTI等[4]研究了一个基于偏最小二乘判别分析(PLSDA)的多元统计模型，在现场测试阶段对葡萄霜霉病的预测正确率约为81%。传统的预测方法对葡萄霜霉病的预测准确率较低且耗时较长。随着非线性预测理论的发展，有学者尝试用BP神经网络对葡萄霜霉病进行预测[5–6]。魏开来[7]通过温度、相对湿度等4个气象因子，构建了基于BP神经网络的葡萄霜霉病预测模型，实现了对霜霉病病情指数的预测，通过MAPE方法计算出的模型预测精度为72.98%。使用BP神经网络建立的病害预测模型需要大规模样本数据，而葡萄霜霉病预测是小样本预测问题，所以容易致使BP网络陷进局部最优。支持向量机(SVM)[8]具有泛化能力强、适合小样本学习等优点。宋旺[9]尝试利用SVM建立对葡萄霜霉病预测的模型，通过对比发现预测效果优于传统的多元线性回归模型，但是相关性仅为71.35%，且其关于葡萄霜霉病预测因子和SVM训练参数的选择没有进行进一步的探讨。

为了更好地实现对葡萄霜霉病发病程度的预测，笔者对2012年北京市房山区波龙堡酒庄的气象数据和霜霉病病害数据进行预处理，运用灰色关联分析法(GRA)筛选出与葡萄霜霉病发病等级关联度高的气象因子，作为SVM模型的输入特征向量，通过PSO算法优化SVM的参数，构建基于GRA–PSO–SVM的预测模型，实现对未来1 d的葡萄霜霉病发病等级的短期预测，并与改进网格搜索法优化的SVM、不同核函数的标准SVM、不同训练函数和粒子群算法优化的BP模型进行比较，以期建立预测能力更好的模型，更精确有效地预测葡萄霜霉病。

1 材料与方法

1.1 数据来源

选择 2012年北京市房山区波龙堡酒庄的‘霞多丽’葡萄品种作为研究对象。气象数据由附近自动气象站以1 h间隔测量并记录，包括温度、相对湿度、降水、风速、光照、水含量等。葡萄霜霉病发病率(逐日调查)和病情指数(每隔6 d调查1次)数据由北京市农林科学院植物保护环境保护研究所提供。

1.2 病害数据处理

将葡萄霜霉病病情指数和发病率随时间的变化绘制成流行曲线(图1)。2012年北京市房山区葡萄霜霉病的发病流行情况符合Logistic模型[10]，即在6月24日发现第1枚病叶开始，病情指数和发病率在始发期内缓慢增长；到达拐点后，病害进入盛发期，病情指数和发病率呈指数增长；从8月下旬开始，病害处于衰退期，霜霉病病情趋于稳定。

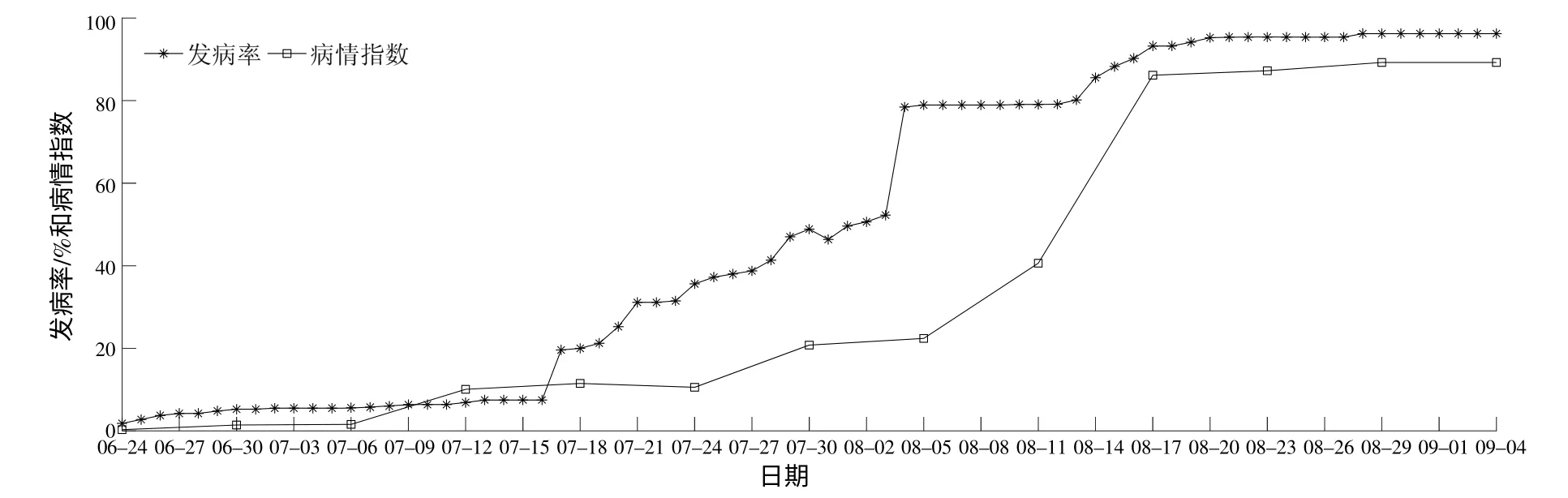
图1 2012年房山区葡萄霜霉病流行曲线Fig.1 Epidemic curve of the grape downy mildew in Fangshan district in 2012

依据文献[11]，将葡萄霜霉病的日发病程度轻重分成5级，1级，轻发生；5级，大发生。模型输出的葡萄霜霉病病害等级由轻至重用1、2、3、4、5进行标识。

1.3 基于灰色关联分析的气象数据预处理

鉴于葡萄霜霉病的发生、流行与温度、相对湿度和降水密切相关[3,12]，葡萄霜霉病单次侵染的时间一般为5 ~7 d[13]，因此，选择将病害调查日前7 d的温度和相对湿度进行整理，得到7 d 平均温度、7 d最高温度、7 d 最低温度、7 d 平均相对湿度、7 d最高相对湿度和7 d最低相对湿度。将自6月17日开始至病害调查日前1 d的降水量和降水天数进行累计，得到最终累计降水量和累计降水日，整理这8个因子，依次用X1、X2、…、X8表示。

把葡萄霜霉病发病等级作为参考序列y(k)，气象因子作为比较序列xi(k)，通过灰色关联分析法(GRA)[14]计算整理得到的8个气象因子和葡萄霜霉病发病等级之间的灰色关联系数和灰色关联度，对应计算公式如(1)、(2)[15]，对灰色关联度排序筛选出与葡萄霜霉病变化态势最相近的气象因子。

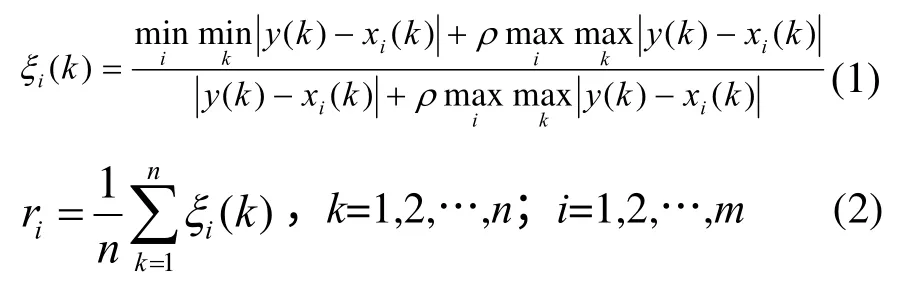
通过MATLAB编辑好的程序进行灰色关联度分析，最终气象因子与发病等级的关联度为r1=0.595 1；r2=0.593 8；r3=0.567 0；r4=0.620 4；r5=0.611 2；r6=0.646 9；r7=0.694 7；r8=0.875 7。

对关联度进行排序，选择关联度较大(ri>0.62)的4个因子作为葡萄霜霉病预测的气象因子，即平均相对湿度、最低相对湿度、累计降水量和累计降水天数。

2 灰色关联和PSO–SVM结合的葡萄霜霉病预测模型的建立

2.1 模型数据的归一化处理

模型的输入数据使用GRA确定的4个气象因子，输出数据是进行病害数据处理得到的未来 1 d的葡萄霜霉病病害等级。由于所采集数据的量纲不同，当使用PSO–SVM 模型预测葡萄霜霉病时，通过归一化公式[16]对已量化的样本数据进行标准化操作，使其转化为[0，1]之间的数，从而消除不同维度数据间的量纲差别。

2.2 葡萄霜霉病预测的多分类支持向量机构造

使用非线性SVM构建葡萄霜霉病预测模型。鉴于葡萄霜霉病预测属于多分类问题，还需对非线性SVM模型作进一步改进。葡萄霜霉病发病等级共 5个级别，通过“一对一”SVM 算法实现葡萄霜霉病预测的5分类问题，构建10个二分类器，对测试样本进行分类并通过投票的方法进行类别决策[17]。每个SVM二分类器分类时，把能区分样本并使正反例间隔最大的优化问题表示成:

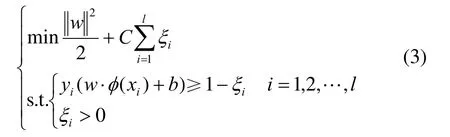
式中：w为权值向量；b为偏置项；C为惩罚因子；ξi表示松弛项；yi表示所属类别，取{–1，+1}；φ(x)是原数据x在高维特征空间的对应值。

通过二次规划方法求解，最终求解得到的最优分类函数。

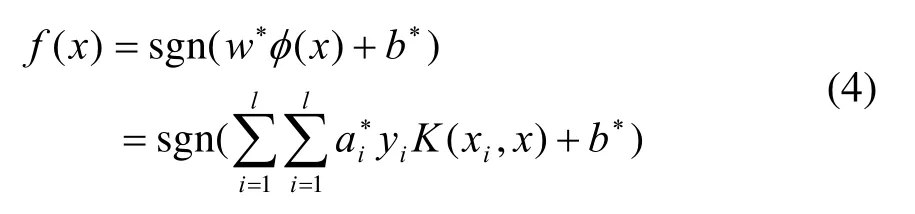
K(xi,x)即为在高维空间中代替点积运算的核函数。研究使用径向基核函数作为SVM模型的核函数，其表达式为

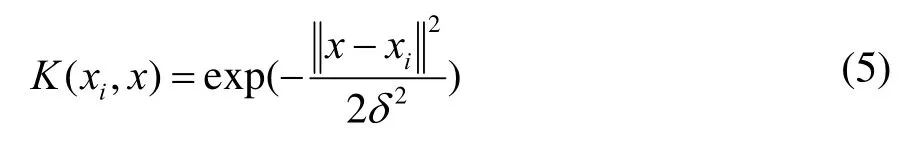
2.3 基于灰色关联和PSO–SVM的葡萄霜霉病预测模型

改进后的SVM模型可以用有限的训练测试样本得到尽可能小的误差，具备很强的泛化能力。为了提高模型泛化能力所选择的径向基核函数，其惩罚因子C和核参数δ的选取对SVM模型的预测正确率影响颇大，以往根据经验选择具有一定的盲目性。因此结合粒子群算法(PSO)[18]的全局寻优能力对参数C和δ进行优化，直至得到最优解，构建葡萄霜霉病预测的GRA–PSO–SVM模型(图2)。首先通过灰色关联分析，归一化等预处理得到葡萄霜霉病短期预测的训练测试样本集。

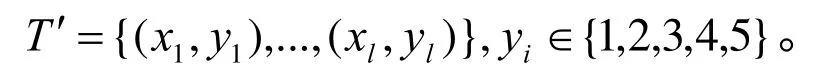
上式中yi对应模型输出数据，也就是葡萄霜霉病病害等级，其值分别代表葡萄霜霉病5种发病级别。参照文献[19]，初始化PSO–SVM模型的基本参数，选取SVM 模型的预测正确率作为适应度函数，计算比较每个粒子的当前适应度值，更新个体极值Pi和全局极值Pg；然后根据公式(6)、(7)调整当前粒子的速度和位置，并判断粒子群的全局极值是否满足要求或者是否到达寻优次数的阈值，迭代寻找全局最优位置对应的最优C和δ；最后将最优参数C和δ放进模型训练，得到全局最优GRA–PSO–SVM的预测模型，开展葡萄霜霉病病害等级预测。

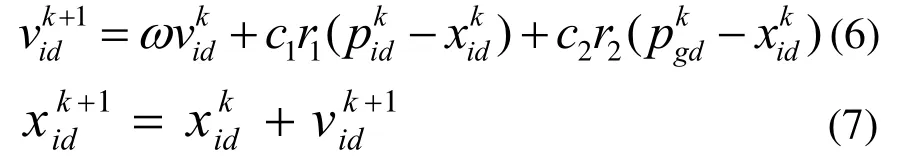
图2 基于GRA–PSO–SVM模型的葡萄霜霉病预测流程Fig.2 Forecasting process of the grape downy mildew based on GRA-PSO-SVM model

3 结果与分析

3.1 模型预测结果

选取 70个具有代表性的样本数据，以灰色关联分析确定的平均相对湿度、最低相对湿度、累计降水量和累计降水天数作为预测因子，建立基于灰色关联和PSO–SVM的葡萄霜霉病短期预测模型，预测未来1 d的葡萄霜霉病病害等级，其中49个作为训练样本集，21个作为测试样本集用于测试检验。借助 Matlab软件和 Libsvm工具箱编写GRA–PSO–SVM预测模型的算法程序，模型的初始参数作如下处理：粒子群规模为20，迭代次数k为200，学习因子c1=1.5，c2=1.7，惯性权重ω=1，惩罚因子C在[0.1，100]取值，核函数参数δ的寻优范围[0.01，1 000]，以SVM模型的预测正确率作为粒子适应度评判依据。图3–左是粒子群的适应度曲线，可以发现随着种群的寻优次数逐渐增加，适应度也在逐渐提高，经过粒子群算法优化参数后的SVM预测模型具有较好的收敛效果，优化得到的较优参数组合为C=6.310，δ= 7.294。再将优化后的参数C和δ代入SVM重新训练模型，得到基于灰色关联和PSO–SVM的葡萄霜霉病预测模型，其对测试样本的预测结果如图3–右所示，模型的预测结果与葡萄霜霉病实际病害等级数据较为一致，预测正确率达95.24%。

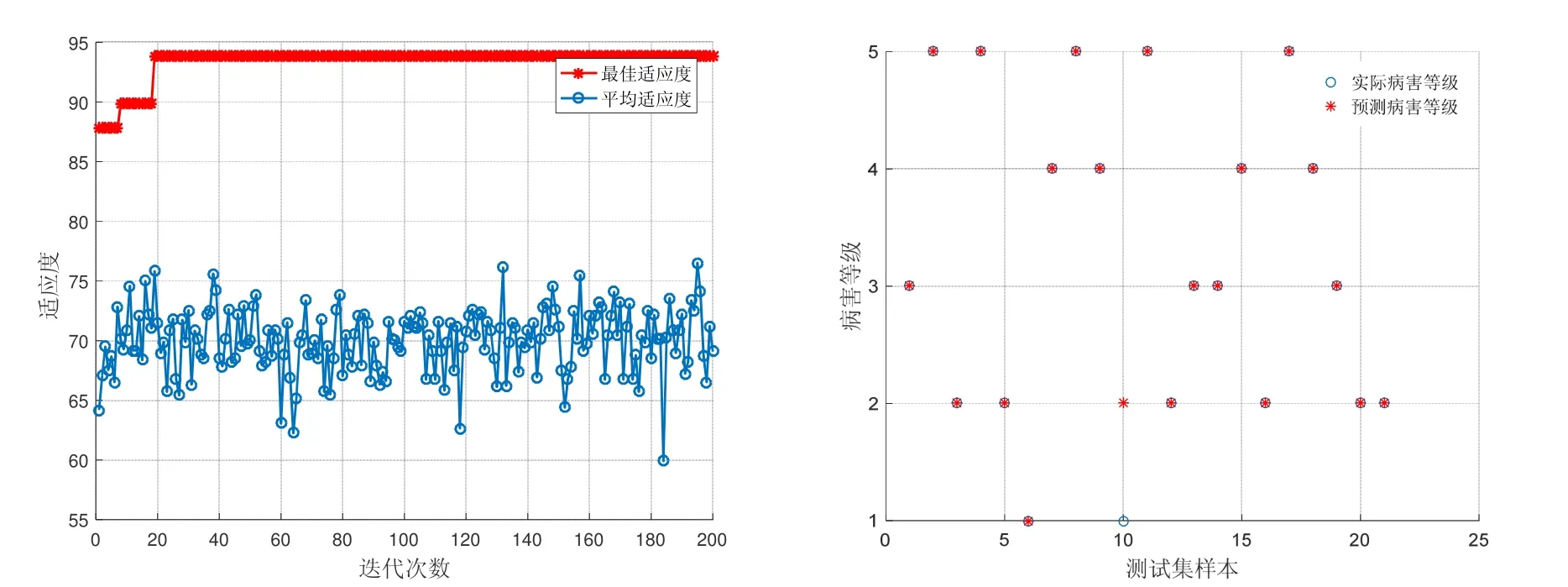
图3 基于GRA–PSO–SVM的葡萄霜霉病预测等级Fig.3 Prediction level of the grape downy mildew based on GRA-PSO-SVM

3.2 预测因子验证

比较分析原始气象因子和经过灰色关联分析处理后的气象因子，应用PSO–SVM模型对葡萄霜霉病病害等级进行预测，连续试验4次，预测结果列于表1。其中PSO–SVM模型使用的是原始气象因子，GRA–PSO–SVM模型使用的是经过GRA处理后的气象因子。结果GRA–PSO–SVM模型4次平均预测正确率达到95.24%，略高于基于原始气象因子的PSO–SVM模型的预测结果(94.05%)；基于灰色关联分析的PSO–SVM模型的平均运行时间为8.95 s，相比于使用原始气象因子，模型运行时间缩短了1.81 s。由此可见，灰色关联分析确定的预测因子确实是与葡萄霜霉病变化趋势具有较高的关联度，结合了 GRA的模型预测更准确，运行速度更快。

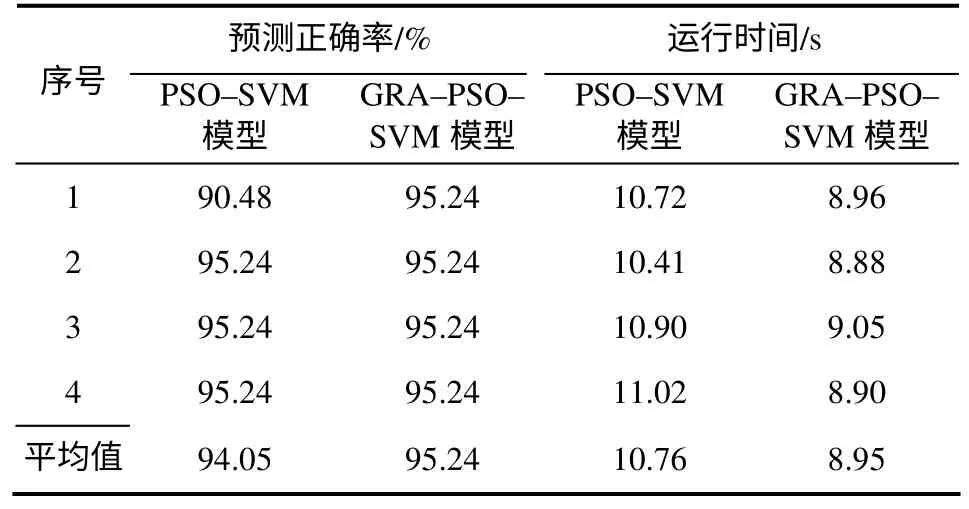
表1 基于不同气象因子的PSO–SVM模型的霜霉病预测的正确率及运行时间Table 1 Prediction results of the downy mildew based on PSO-SVM model with different meteorological factors

3.3 模型比较

3.3.1 改进网格搜索法优化对比

为了测试粒子群算法对SVM参数选择的有效性，同等条件下采用改进网格搜索法(GS)[20]优化参数C和δ，对比分析2种优化模型的预测效果。先后对SVM参数进行大步距的粗略搜索和小步距的精细搜索，粗略选择的参数C和δ的搜索范围为[2–10，210]，步距为1；精细选择的参数C和δ的搜索范围为[2–4，24]，步距为0.5。粗略选取SVM参数的过程见图4–左，2次搜寻得到的最优参数为C=11.314，δ=2.828。图4–右显示的是基于GRA和改进网格搜索法的SVM模型的预测结果，预测正确率达到 90.48%，略低于 PSO算法的预测结果(95.24%)，由此可见，PSO–SVM 模型相比于改进GS–SVM模型的预测效果更好。

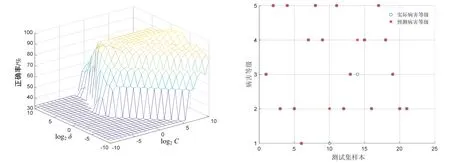
图4 基于GRA–GS–SVM的葡萄霜霉病预测等级Fig.4 Prediction level of the grape downy mildew based on GRA-GS-SVM

3.3.2 预测模型与其他机器学习模型比较

对 PSO–SVM 模型有效性和优越性的验证，在确保灰色关联分析得到的试验数据不变的前提下，分别采用经验选择参数的标准SVM、改进网格搜索法优化的SVM、不同训练函数和粒子群算法优化的BP网络进行葡萄霜霉病病害等级预测，并将其与PSO–SVM 模型进行比较，预测对比结果如表2所示。分别使用不同核函数的标准SVM进行预测，结果所用的径向基核函数具有较好的预测效果。同时使用径向基核函数时，C和δ的取值不同，模型的预测结果也不同。采取PSO方法和改进网格搜索法优化支持向量机减少了参数选取的随机性，模型预测正确率更高，其中粒子群算法的优化效果最好。

表2 基于不同机器学习模型的霜霉病预测的正确率Table 2 Prediction accuracy of the downy mildew based on different machine learning models

由表2可知，使用粒子群算法优化的BP模型的预测效果更好，预测正确率达到93.33%，但低于PSO–SVM模型的预测正确率95.24%。traingd函数的BP模型对葡萄霜霉病的预测正确率低于50%，可见对梯度下降的依赖极易导致BP网络陷进局部最小。虽然使用GRA+BP(训练函数a)模型和粒子群算法提高了BP模型的预测正确率，但BP网络结构的难以确定、收敛速度慢等缺点影响了模型的预测效果。

4 结论与讨论

设计的基于灰色关联和PSO–SVM的葡萄霜霉病预测模型，可实现对葡萄霜霉病发病严重程度的短期预测。引入灰色关联分析法，确定与葡萄霜霉病变化态势最相近的气象因子，相比于使用原始气象因子，有效提高了模型的预测速度和正确率；为了减小随机选择惩罚因子C和核函数参数δ的误差，采取PSO算法优化SVM模型参数，通过与改进网格搜索法优化的 SVM、经验选择参数的标准SVM、不同训练函数和粒子群算法优化的BP方法进行比较，得出基于 GRA–PSO–SVM 的模型预测效果更好。该模型还有一定的局限性，模型数据都是基于小样本系统。后续研究重点应是增加样本数据，并改进粒子群算法，以实现对不同年份、多个葡萄品种的霜霉病发病程度的有效预测。