航天器陨落落点计算偏差分析

淡 鹏，王 超，王 丹

(1.宇航动力学国家重点实验室，陕西 西安 710043；2.西安卫星测控中心，陕西 西安 710043)

0 引言

陨落落点计算是航天器发射过程、寿命末期离轨控制和空间物体异常再入等任务中经常需要计算的内容，准确预报陨落落点对于飞行弹道设计、飞行任务组织等都有着重要意义。因此，落点计算也得到了较多研究，文献[1-3]对落点计算方法进行了研究和阐述；文献[4-7]对落点统计或计算过程中的单个影响因素进行了分析。

由于受多种因素的制约，在落点计算中，预报的陨落落点往往与实测落点有一定差距，分析陨落落点偏差产生的原因以及常见因素导致的偏差量量级对于提高落点计算精度、预估落点误差范围等都有着重要意义。目前关于陨落落点的文献大多集中于计算方法、落点统计方法等方面，对精度的分析较少。本文在给出陨落落点计算方法的基础上，对各类摄动力的对比、大气阻力参数的影响、径切法方向加速度对比及初始位置速度误差影响等方面进行了分析。

1 陨落落点计算方法

由于航天器飞行过程中通常采用J2000惯性系或地心固连系(如WGS84坐标系)下的位置、速度来表示运动状态[8-9]，而这2种坐标系间可通过岁差、章动、自转及极移矩阵实现相互转换，本文以常用的J2000惯性系位置速度数据(分别记作r，v)作为初值进行陨落落点积分计算。

在航天器陨落过程中，主要受到地球引力、月球引力、太阳引力、太阳光压摄动、大气作用力及其他力(如潮汐力及其他经验力)的作用，设这些力产生的加速度依次为aearth，amoon，asun，alight，agas，aelse，则陨落过程位置速度外推模型为：

(1)

在某个时刻，由位置矢量r可计算出当前的经度、纬度和高度。

通过对式(1)进行积分运行并查看和判断每个时刻的高程值即可计算出陨落落点。

式(1)中，其他力的量级较小，此处暂不考虑。而大气阻力在地心固连系下加速度为：

(2)

式中，CD为阻力系数；ρ为航天器所在空间的大气密度；S/m为航天器面质比；v为航天器相对大气的速度(其大小为v)。

大气密度的数值通常采用经验大气模型来计算，本文采用NRLMSISE-00大气密度模型[10-11]，它是由美国海军研究实验室在MSISE-90模型基础上发展而来的一种大气密度模型，在航天器飞行任务中得到了较多应用。

2 计算及分析

为分析航天器陨落落点偏差及其影响因素，给定如下算例，并在此基础上进行分析。

算例(仿真数据)历元时间为2019-05-30 06:54:36.9，地心固连系位置矢量为[-1 854 368.8，4 719 592.2，3 961 405.2](单位：m)，速度矢量为[-441.06，2 071.71，-981.79](单位：m/s)，面质比取为0.005 876(单位：m2/kg)。采用NRLMSISE-00模型进行大气密度计算，给定KP值2.0，F107，F107A值均为70。

2.1 各类摄动力对比计算

截取飞行过程中65 km及10 km高度处的摄动力加速度(单位:m/s2)及大气密度(单位：kg/m3)，计算结果如表1所示。

表1 加速度及大气密度对比

Tab.1 Comparison between acceleration and atmospheric density

由表1可以看出，对于该算例，在陨落过程中，太阳引力、月球引力产生的加速度的量级为10-7，太阳光压加速度量级为10-8。因陨落过程一般时间较短(约几分钟到几十分钟，此时间内这几个小量加速度累积产生的位置偏差较小)，由一维状态下的匀加速位移公式s=v0t+a0t2/2(s，v0，a0，t分别为位移、初始速度、加速度及时间增量)可知，陨落过程中，太阳引力、月球引力及太阳光压对位置的影响很小，可忽略不计。地球引力(约9.8 m/s2)与大气阻力(加速度10-1～101量级)是陨落过程中的主要作用力，且不同高度处二者产生的加速度大小差异显著，甚至在本算例中出现了10 km处大气阻力加速度大小超过地球引力加速度的现象。

为分析该现象产生的原因，根据式(2)，在阻力系数和面质比一定情况下，加速度大小主要取决于大气密度[12]及飞行速度。

飞行过程随高度减小时计算的大气密度变化情况如图1所示。

图1 大气密度随高度变化曲线Fig.1 Variation curve of atmosphericdensity with altitude

由图1可以看出，靠近地面处，大气密度达到约1.2 kg/m3，远远大于85 km以上的量值。特别是在大气对流层(十余千米)以内，密度值较大，这与对流层大约集中了整个空气质量的将近3/4有关。

计算的飞行过程地球引力加速度、大气阻力加速度及总加速度大小对比如图2所示(相对时间为相对算例起始历元的秒数)。

图2 飞行过程加速度大小对比Fig.2 Comparison of accelerations during flight

由图2可以看出，开始一段时间，大气阻力加速度小于地球引力，总加速度与引力加速度接近；而后面部分时段，大气阻力加速度比地球引力加速度大，合成加速度接近大气阻力加速度，也就是说大气阻力将对飞行速度产生显著的“减速效果”。这是该算例飞行变化的重要特点。

2.2 大气阻力参数影响

根据分析，大气阻力对陨落过程影响显著，对式(2)中另外2个重要参数是阻力系数CD与面质比。

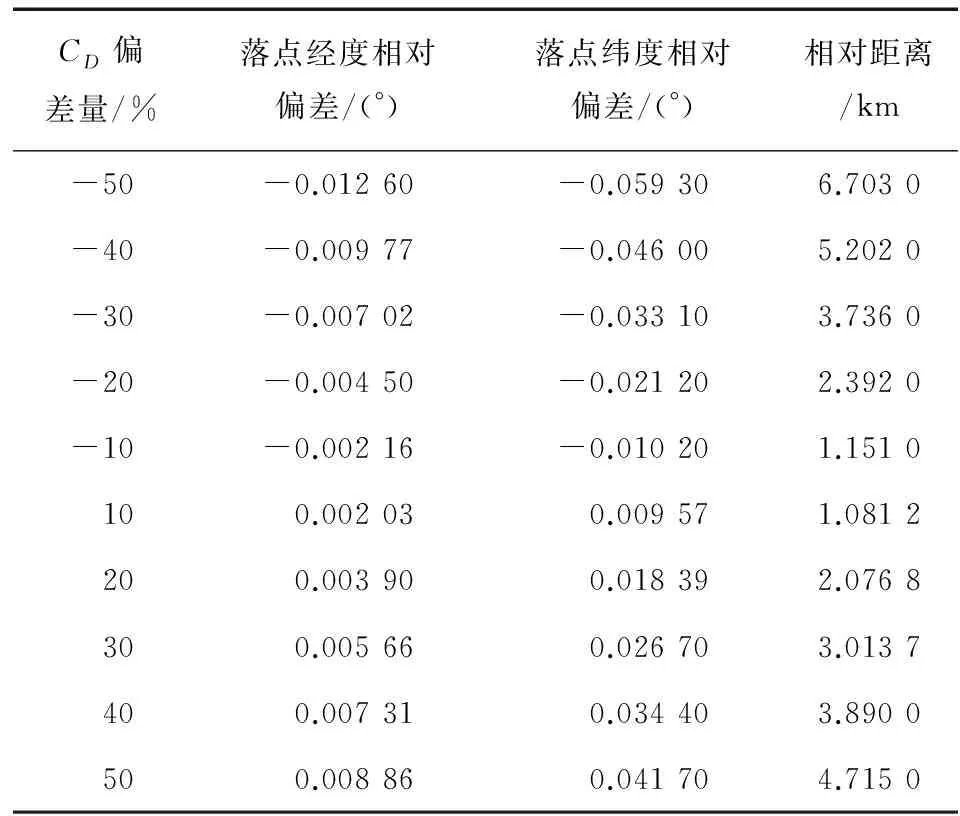
以CD取1.0时落点为基准，为CD值添加不同百分比的偏差增量，计算的落点偏差对比如表2所示。

表2 不同CD下落点偏差对比
Tab.2 Comparison of deviations with differentCDvalue

CD偏差量/%落点经度相对偏差/(°)落点纬度相对偏差/(°)相对距离/km-50-0.012 60-0.059 306.703 0-40-0.009 77-0.046 005.202 0-30-0.007 02-0.033 103.736 0-20-0.004 50-0.021 202.392 0-10-0.002 16-0.010 201.151 0100.002 030.009 571.081 2200.003 900.018 392.076 8300.005 660.026 703.013 7400.007 310.034 403.890 0500.008 860.041 704.715 0

由表2可以看出，不同的阻力系数误差量级对落点结果产生了较大影响，10%以上的阻力系数偏差导致的落点误差均在1 km以上，且变化较大。

实际飞行中阻力系数与马赫数、高度及烧蚀程度等因素均有关，是变化的量，若能得到更精细的阻力系数模型，对提高落点精度有一定帮助。

对式(2)，另一个固定系数为面质比，对其给定不同偏差，也将得到km量级的落点偏差。

2.3 RTN不同方向影响分析

除了距离偏差，落点的偏差还常常表现在弹道飞行方向垂线上的偏离量。

考虑陨落飞行过程最主要的2种力：地球引力和大气阻力。地球引力中最主要的J2项在地心矢径(径向)和地球自转轴矢量we方向上产生的加速度分量gr,gw为：

式中，J2=1.082 63×10-3为二阶带谐项系数；μ=3.986 005×1014m3/s2为地球引力常数；Re为地球赤道半径；r=[x,y,z]T，为地心惯性系下位置分量(矢量r的模记作r)。

考虑到飞行速度与自转轴的夹角，在切向与法向方向均产生分量，地球引力将对弹道径、切、法方向均产生加速度。

由式(2)可以看出，大气阻力加速度主要沿着速度反方向，故在径向、切向都存在分量。同时，考虑到大气随着地球自转，在法向上也将产生加速度。

为分析落点在弹道飞行方向垂线上的偏离量，考虑飞行过程径向R、切向T、法向N三个方向[13-14]上的加速度变化。RTN方向与速度方向示意如图3所示。

图3 RTN及飞行速度方向示意Fig.3 Schematic diagram of RTN and flight speed direction

以本节算例为例(其初始速度方向朝着南方)，计算地球引力、大气阻力在R，T，N方向加速度分量对比如图4所示。

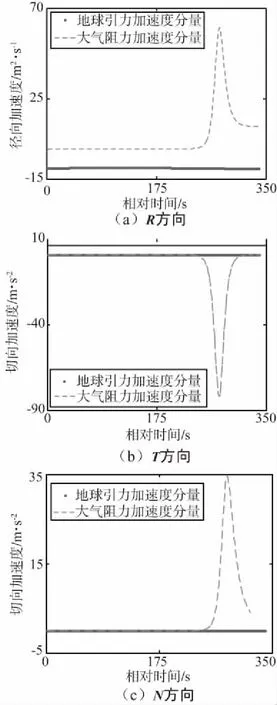
图4 RTN方向加速度对比Fig.4 Comparison of RTN direction accelerations

由图4可以看出，地球引力在RTN方向分量变化较小，但都不为0。大气阻力分量变化较大(这是由大气密度的显著增加造成的。地球引力与大气阻力在弹道垂线方向都有加速度分量)。

2.4 初始位置速度影响

由于航天器的跟踪测量数据(外测、GNSS等)不可避免地存在误差，导致初始位置速度值存在一定偏差[5,15-16]，从而对落点计算精度造成了一定影响。为探讨初始位置、速度偏差下的落点误差，将阻力系数固定为1.0，并固定初始位置，对初始速度分别在不同方向上增加1 m/s的增量；然后固定速度，给初始位置分别在不同方向上增加100 m的增量(定义增量矢量在TN平面投影与T方向夹角为α，增量矢量与TN平面夹角为β，给定不同的角度值，使得增量方向改变)。2种条件下计算的落点偏差(相对于未加位置、速度偏差时)曲线如图5所示(图中dis表示落点距离偏差)。

图5 添加不同偏差量后落点偏差Fig.5 Falling point deviation after adding different deviations

由图5可以看出，添加不同方向的位置(大小100 m)偏差后，导致落点产生了0～13 km的偏差；添加不同方向的速度(大小1 m/s)偏差后，导致落点产生了0～37 km的偏差。可见速度偏差对落点影响显著。

考虑到航天器飞行过程中一般速度项较难测定或获得精确值，且分离力等其他力更易对速度项造成影响，因而在计算中需要更注意速度项的误差影响。

3 结束语

本文对航天器陨落落点偏差的影响因素进行了探讨，分析了其产生的原因，通过算例分析给出了影响的量级。从计算结果可得出：① 陨落过程中，太阳引力、月球引力及光压摄动等作用力的量级小，故在飞行时间较短时可以不予考虑；② 大气参数对陨落落点位置偏差影响显著，大气作用下可对陨落过程起到显著的减速作用，在部分时段大气阻力加速度甚至超过了地球引力。在初值相同的情况下，给定不同的大气参数可能会导致千米量级的偏差；③ 初始速度的大小及方向偏差将对落点结果产生较大影响；④ 地球引力及大气阻力在飞行弹道的径向、切向及法向都存在分量，也就是说其将对落点经纬度等方向上的偏差均造成影响。而法向分量会使得落点偏离原弹道方向。

为提高陨落落点预报精度，首先应精确计算出初始的位置速度，其次要合理设定大气计算的相关参数。航天器陨落过程计算受很多复杂因素制约，要提高计算精度，需要在初值精度、大气参数及大气模型等多方面综合努力。下一步将重点在大气的精细化建模与初始位置速度的精确确定上进行研究。