无限长矩形波导中二能级原子的自发辐射
2020-05-17刘延李梦薇甄灵敏宋亚菊
刘延,李梦薇,甄灵敏,宋亚菊
(衡阳师范学院 物理与电子工程学院,湖南 衡阳 421002)
波导量子电动力学旨在研究受限于波导系统的电磁场和原子之间的相互作用,在分布式量子计算和量子网络等领域都具有重要的理论研究意义和广泛的应用价值。波导中原子自发辐射诱导的量子退相干是阻碍波导量子电动力学在各领域的应用和发展的主要因素。研究波导量子电动力学中光与物质的相互作用,特别是波导中原子的自发辐射,已成为一个亟待解决的热点问题。
近年来,波导量子电动力学引起了国内外理论和实验物理学者的广泛关注和深入研究。美国哈佛大学Lukin 研究组在2007 年基于波导系统提出了单光子晶体管方案[1]。随后, Kimble 等人在2008 年首次提出了分布式量子网络的概念[2]。斯坦福大学的Shanhui Fan 研究组利用广义Bethe-ansatz方法推导出波导系统中少光子的精确S 矩阵[3]。国内孙昌璞和周兰研究小组基于一维耦合腔波导[4-5],也相继提出了多种单光子量子相干器件的理论方案,并在弱耦合区域利用Weisskopf-Wigner 近似研究了矩形波导中二能级原子的自发辐射特性[6-11]。尽管波导量子电动力学的研究取得了一些显著的研究成果,但我们发现大多研究者基于具有线性色散关系的一维理想波导系统。而实际波导的非线性色散特性会诱导波导与原子耦合系统出现本征束缚态,会极大影响波导中原子的长时动力学行为[12-14],这在量子存储方面具有潜在的应用价值。因此,研究由波导系统非线性色散诱导的束缚态及其量子效应成为该领域另一个亟不可待的科学问题。
本文将以无限长矩形波导与二能级原子耦合系统为例,利用Lippmann-Schwinger 方程和不含时薛定谔方程分别推导出耦合系统的本征散射态和本征束缚态,进而求得耦合系统的时间演化算符,深入探究原子的自发辐射特性,揭示在二能级原子在矩形波导中的稳态相干囚禁现象及其物理机制。该研究不仅有助于人们深入认识微观世界中光与物质相互作用的物理规律[15],而且有望为基于波导量子电动力学系统的量子信息处理提供更优的量子调控方案,实质性地推动波导量子电动力学系统在量子计算、量子通信等领域的应用。
1 物理模型及其哈密顿量
如图1 所示,单个二能级原子处于横截面高为a、宽为b 的无限长矩形波导正中央。考虑二能级原子的电偶极矩方向沿z 轴。由于矩形波导的TE传播模式在z方向的分量Ez=0 ,在电偶极近似下,二能级原子只与矩形波导的TM 模式耦合。简单起见,本文仅讨论二能级原子与单个TM11模式耦合。此时,总系统的哈密顿量为


图1 二能级原子与无限长矩形波导耦合系统示意图
2 本征态求解
在旋转波近似下,耦合系统的总激发数守恒。在单激发子空间,总系统的本征散射态可表示为


由此可知,总系统的本征散射态由(5)式和(8)—(12)式共同决定。

3 二能级原子的自发辐射
根据二能级原子与矩形波导耦合系统的本征散射态和束缚态,总系统的时间演化算符可以表示为

从上式可以看,二能级原子激发态布居数的动力学由总系统本征散射态和本征束缚态两部分的共同调制,其中束缚态的出现导致二能级原子出现激发态布居数囚禁现象,而不同散射态之间的量子干涉和束缚态和散射态之间的量子干涉导致二能级原子激发态布居数的衰减。
接下来,我们将详细分析原子跃迁频率Ω 与矩形波导截止频率ωc的失谐,以及原子与矩形波导耦合强度g对原子激发态布局数动力学的影响。
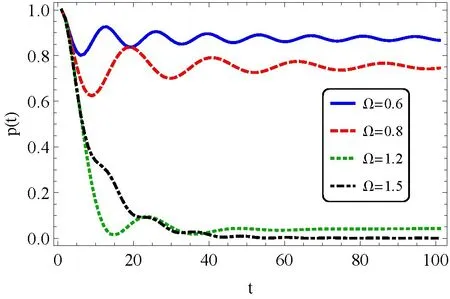
图2 二能级原子跃迁频率Ω取不同值时,原子激发态布居数p(t)的动力学演化,其中原子与波导的耦合强度g =0.1。
图2 给出了二能级原子激发态布居数的动力学演化p(t) 与原子跃迁频率Ω 的关系,其中矩形波导TM11模的截止频率ωc为单位频率,原子与矩形波导的耦合强度取为g=0.1。由图2 可知,原子的激发态布居数随时间震荡衰减,而且当时间趋于无穷大时,激发态布局数趋于恒定值。此外,对比图2 中的四条曲线,可知当原子的跃迁频率越低于矩形波导的截止频率时(Ω/ωc=0.6,0.8),原子激发态布居数的震荡越明显,而且激发态布居数在稳态下数值越大,出现可观的激发态布居数囚禁现象。相反,当原子的跃迁频率高于矩形波导的截止频率时(Ω/ωc=1.2,1.5),原子与矩形波导发生共振,自发辐射的衰减现象更明显,而且激发态布居数在稳态下的数值较小。
图3 和图4 反映了原子与矩形波导的耦合强度g对激发态布居数p(t)的影响,其中矩形波导TM11模的截止频率ωc为单位频率,原子跃迁频率分别取Ω =0.8 和Ω =1.5。可知随着耦合强度g的增强,原子激发态布居数的震荡和衰减都越明显。对比图3 和图4 中原子与矩形波导耦合强度取相同值的曲线,可知原子激发态布居数动力学演化的整体趋势主要受原子跃迁频率Ω 的影响。
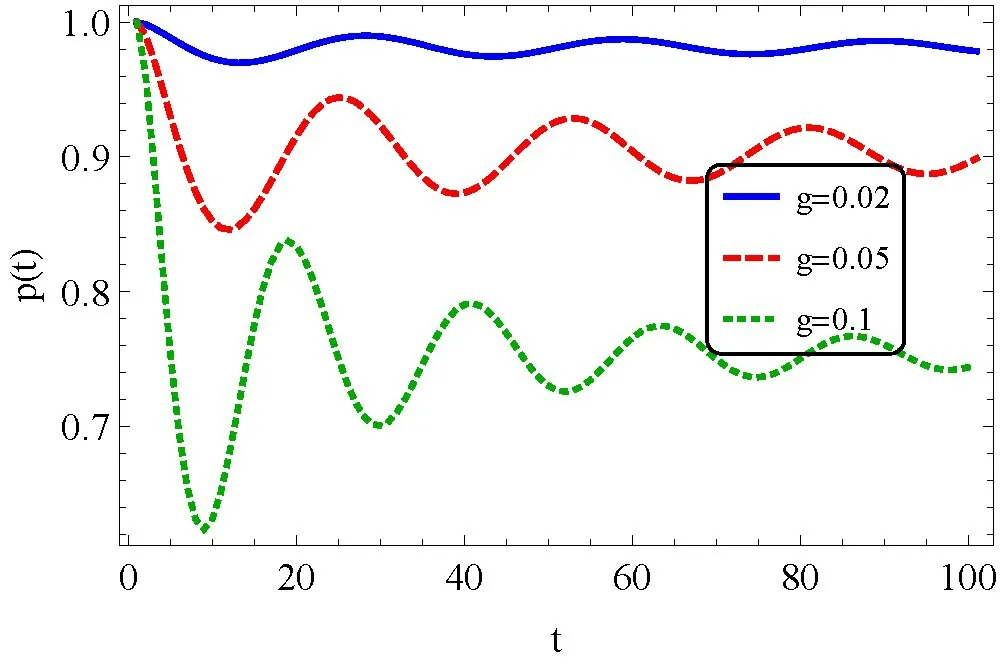
图3 二能级原子与波导的耦合强度g 取不同值时,原子激发态布居数p(t)的动力学演化,其中原子的跃迁频率Ω=0.8。

图4 二能级原子与波导的耦合强度g 取不同值时,原子激发态布居数p(t)的动力学演化,其中原子的跃迁频率Ω=1.5。
4 结束语
本文主要研究了二能级原子在无限长矩形波导中的自发辐射特性。我们在电偶极近似和旋转波近似下,利用Lippmann-Schwinger 方程和不含时薛定谔方程分别求出总系统的束缚态和散射态,进而推导出时间演化算符和原子激发态布居数的动力学演化。研究表明,二能级原子的激发态布局数随时间震荡衰减,而且由于束缚态的存在,当时间趋于无穷大时,激发态布居数趋于恒定值。我们还进一步分析了原子跃迁频率和原子与矩形波导之间耦合强度对二能级原子自发辐射的影响。原子的跃迁频率越远离矩形波导的截止频率,原子激发态布居数的震荡越明显,而且激发态布居数在稳态下数值越大,出现可观的激发态布居数囚禁现象;而随着耦合度的增强,原子激发态布居数的震荡和衰减都越明显,并且原子激发态布居数动力学演化的整体趋势主要受原子跃迁频率的影响。本文只考虑了二能级原子与矩形波导单个TM 模式耦合的情况,我们将在后续研究中继续讨论多能级单(多)原子与矩形波导多个传播模式耦合的情况。
