基于SQP算法的概率积分法参数反演

代 阳

(1.安徽理工大学 测绘学院，安徽 淮南 232001；2.矿山采动灾害空天地协同监测与预警安徽省教育厅重点实验室，安徽 淮南 232001)

煤炭在我国能源供给结构中占有主体地位。在地下开采时，矿区岩体受力平衡遭到破坏，引发上覆岩层移动变形，导致地表沉降移动。且随着开采范围的扩大，周边建筑与环境势必受到影响，严重时可能会引发建筑物塌陷、地下水资源被破坏、地表塌陷等地质灾害和次生灾害，严重影响人们的生活安全[1-2]。因此，研究矿区开采引发的地表移动变形规律，在灾害治理与防范中有着重要的意义。

概率积分法是预计矿区开采沉陷变化规律的积分模型，其模型的主要思想是基于LITWINISZYN提出的随机介质理论，利用采空区实测数据拟合得到的预计参数，预测矿区地表移动变化。构建概率积分法模型的关键，在于保证输入预计参数的准确性。由于该模型非线性程度高、参数之间相关性强、求解易受迭代初值影响，采用传统的求解参数方法往往会带来局部解甚至无解[3]。为解决上述问题，学者们引用了优化及智能优化算法反演模型参数。葛家新等以皖北矿区为例，采用模矢法进行反演参数，拟合预测的下沉效果较好，但易受到参数设计初值的影响[4]。查剑锋等采用遗传算法进行模型参数估计，并与最小二乘法和模矢法相比，证明遗传算法的准确性与稳定性更优[5]。苏军明等采用模拟退火的方法，在搜索最优参数的过程中加入随机因素，更好地得到全局最优解[6]。徐孟强等采用粒子群算法反演参数能够得到准确的预计参数，且在一定范围内受初值误差影响较小[7]。智能优化算法通过模仿自然现象及生物进化规律，迭代逐步逼近参数最优值，然而在搜索的过程中，容易早熟且每次反演得到的参数具有一定的随机性，为构建概率积分模型带来影响[8]。因此，有必要引入新的算法反演概率积分法中的参数。

概率积分法参数反演可以看作是一种非线性多参数求解最优值的过程，提出采用二次序列规划(Sequential Quadratic Programming，SQP)算法反演参数，以达到拟合参数精度最优的目的。SQP算法属于最优化算法，通过二次规划确定每次迭代的下降方向，并通过价值函数获取步长，多次迭代逼近最优值[9]。在处理非线性问题中，SQP算法不依赖于初值，并具有良好的收敛与自我校正能力，结果的稳定性与可靠性强。目前，该算法已经被成功运用于各种非线性最优化问题中，例如在飞机数字化装配[10]、阵列信号处理[11]、高密度电阻率等领域[12]。

根据概率积分模型构建目标函数，引用SQP算法进行参数反演，验证SQP算法运用在开采沉陷预测参数的可能性。通过模拟监测数据受到不同程度的误差及粗差的影响，进行大量仿真实验，将SQP算法是反演结果与常用的优化及智能优化算法作比较，验证SQP算法抗随机误差及粗差的性能。

1 概率积分法预计模型

概率积分法是一种预计由于矿区开采引起的地表沉陷与水平移动的模型[13](P116-120)。其中，预测地表任意点下沉值的函数模型为：

(1)

式中，(x,y)为地表任意点平面坐标；W(x,y)为对应坐标下的地表下沉值；W0(x)为倾向方向充分采动时，横坐标值为x时在走向面的下沉值；W0(y)为走向方向充分采动时，纵坐标为y时在倾向面的下沉值；W0为地表最大下沉值，限于篇幅，W0、W0计算公式见参考文献[13]，不再累述。

预测地表任意点的水平移动值的函数模型为：

(2)

式中，φ为由x轴正向逆时针旋转到指定方向的方位角；U(x,y,φ)为对应坐标下的地表水平移动值；U0(x)为走向主断面上的水平移动值；U0(y)为倾向主断面上的水平移动值。限于篇幅，U0详细计算见参考文献[13]。

概率积分法模型反演参数属于求解多参数最优化极值问题，目的是寻求一组变量，使预测的地表下沉值与水平移动值与实测数据的差值平方和最小。其目标函数的具体表现形式为：

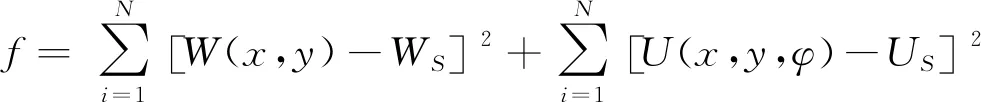
(3)

式中，i为测站数据编号；N为测站的总数目；WS为测站实测下沉观测值；US为测站实测水平移动值。

2 SQP算法的理论基础

SQP算法作为一种应用于非线性函数参数反演的最优化算法，应用于概率积分法反演求参具体表现形式为[14]：

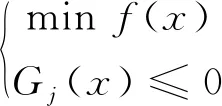
(4)

式中，x=[q,b,θ,tanβ,S1,S2,S3,S4]T为待求优化参数，其中q为下沉系数，b为水平移动系数，θ为开采影响传播角，tanβ为主要影响角正切，S1,S2,S3,S4为对应的下山方向、上山方向、左方向和右方向的拐点偏移距。f(x)对应上文的公式(3)，Gj(x)对应的限制条件，根据矿区情况和需求进行改变。该算法采用拉格朗日求极值法将参数反演转化为求解二次近似函数最优值的问题：

(5)

通过线性化转化后得到QP子问题，其目标函数变换为：

(6)

xk+1=xk+akdk

(7)

式(6)中，d为全变量搜索方向，为梯度，k为迭代次数，Bk为拉格朗日函数的海森矩阵，通过半正定牛顿近似法(Dense quasi-newton approximation，BFGS)进行计算得到[15]。式(7)中，ak为第k次迭代时的步长。

SQP算法反演概率积分模型预计参数的主要步骤为：

1)给定SQP算法反演参数x的初值、为算法反演提供初始解，同时令迭代次数k=0；

2)将反演参数值带入，计算目标函数f(x)及约束函数Gj(x)，差分计算梯度向量值，求解二次规划子问题，计算搜索方向dk；

3)如果dk=0或者xk已经符合精度检验要求，则迭代终止，得到的xk即为该非线性函数的最优解；否则，从点xk沿着dk方向搜索下一步迭代值，并确定步长ak，令xk+1=xk+akdk；

4)通过BFGS算法确定海森矩阵Bk，并转化为正定矩阵。令k=k+1，转至步骤(2)。

3 仿真实验与结果统计分析

3.1 设计工作面概况

依据工作面观测点的设计原则，参考于文献[8]中的工作面，制定模拟矿区的观测线。具体设计为，煤层开采厚度m为4 m、煤层倾角α为3°、工作面的走向长L和倾向长D分别为670 m和300 m、开采深度为260 m，管理顶板为全部垮落法进行管理[8]。概率积分参数的真值分别设计为：下沉系数q为0.64，水平移动系数b为0.3，开采影响角正切值tanβ为2.37，开采影响传播角θ为88.5°，上山方向、下山方向、左方向与右方向的拐点偏移距S1、S2、S3、S4分别设计为52 m。并在矿区上方沿着走向线布设25个监测点(S1～S25)，沿着倾向线布设44个监测点(E1～E44)，各个监测点设计的点位布设，如图1所示。

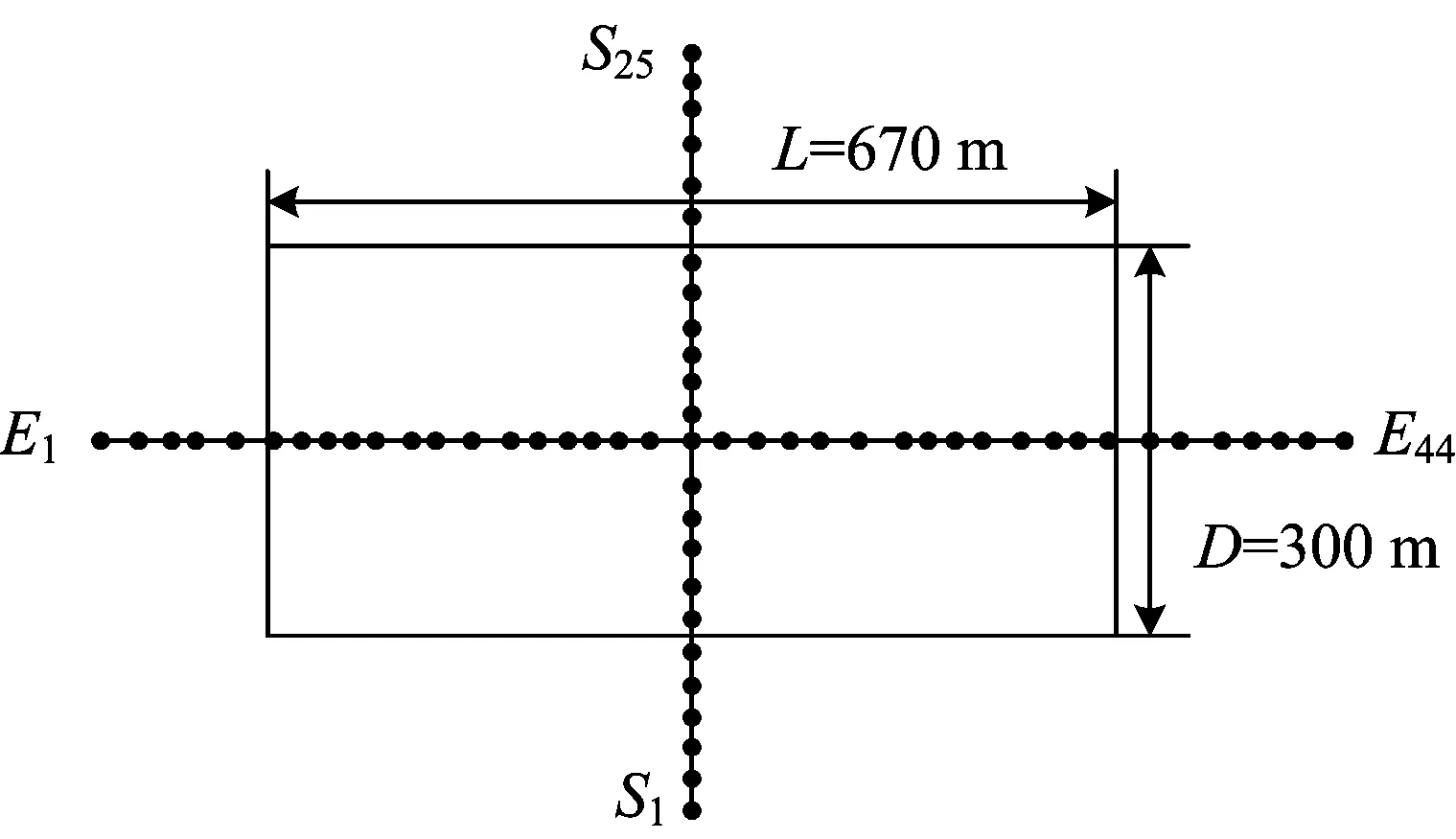
图1 工作面及对应点位模拟图

3.2 SQP算法参数反演准确性分析

以上述S1～S25、E1～E44共69个监测点的下沉与水平移动值作为反演数据的原始数据，结合矿区的基本信息，本文设计了五组不同的参数初始值，将反演结果与真值对比，对算法的稳定性进行评估。同时，通过比较不同初始参数设置下反演结果的差异，验证SQP算法预计参数的结果是否受到初始设计值的影响。

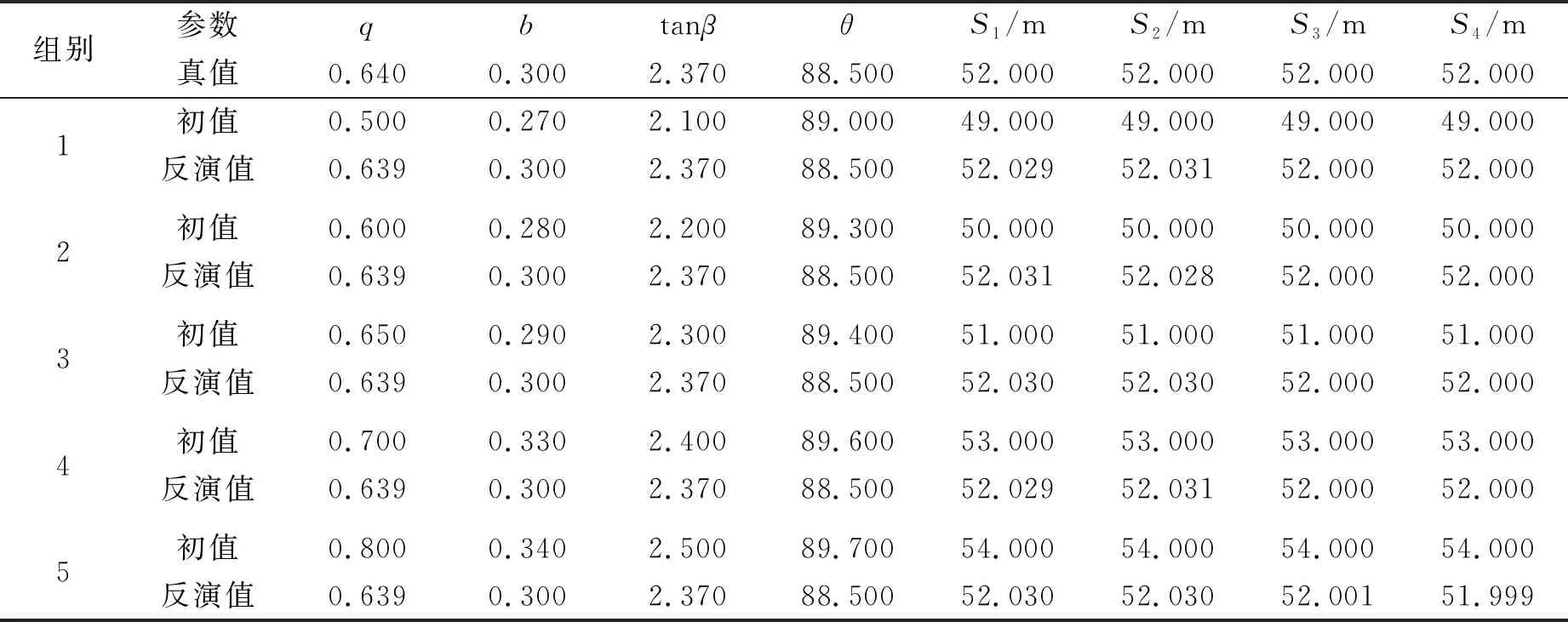
表1 SQP算法反演概率积分法准确性分析

通过分析表1中的反演结果可以得到：1)对比五组不同参数设置下的SQP算法反演结果，随着设置的初始值不断增大，q、b、tanβ、θ与四个方向的拐点偏移距的预计参数并没有发生明显的变化。2)将反演结果与真值对比，参数q、b、tanβ和θ与四个方向的拐点偏移距的预计结果均与真值基本保持一致，相对误差不到1%。根据上述实验结果，验证了SQP算法受到初始值设置的影响很小，且可靠性与稳定性高。

3.3 SQP算法对随机误差、粗差的抗干扰能力

在矿区观测中，观测数据必然会受到随机噪声和粗差的影响，因此测试算法抗随机误差与粗差的干扰能力，是评价算法性能的重要依据。本文模拟多组在不同程度的随机误差及粗差影响下的监测数据，将SQP算法、模矢法与遗传算法进行对比实验，具体步骤如下：

1)设计SQP算法、模矢法与遗传算法的实验参数。模矢法的参数设计为：参数终止步长为0.0001；遗传算法的参数设计为：种群个体数为100，遗传代数为200代，交叉概率为0.9，变异概率为0.001；SQP算法的参数设计为：最大迭代次数200，终止误差为0.0001。每个算法的初始参数的取值范围均为：q∈[0.61,0.67]；b∈[0.25,0.35]；tanβ∈[1.97,2.77]；θ∈[80°,90°]；S1、S2、S3、S4的取值范围均为S∈[32,72]。

2)将设计的采矿条件与沉陷预计参数真值带入概率积分模型中，得到设计工作面观测点的下沉与水平移动值的真值，在真值的基础上分别加入中误差为5 mm、10 mm与20 mm的随机误差，并在不同的随机误差情况下，各仿真20组实验数据，并统计由SQP算法、模矢法与遗传算法反演的各组参数的均值。

3)在实验步骤(1)中的误差为10 mm的仿真数据的基础上，随机选取0～5个观测站的下沉与水平观测值，在此基础上添加5σ-20σ的粗差，并统计由SQP算法、模矢法与遗传算法反演参数的均值。

SQP算法、模矢法与遗传算法反演的参数均值统计值结果，如表2所示。

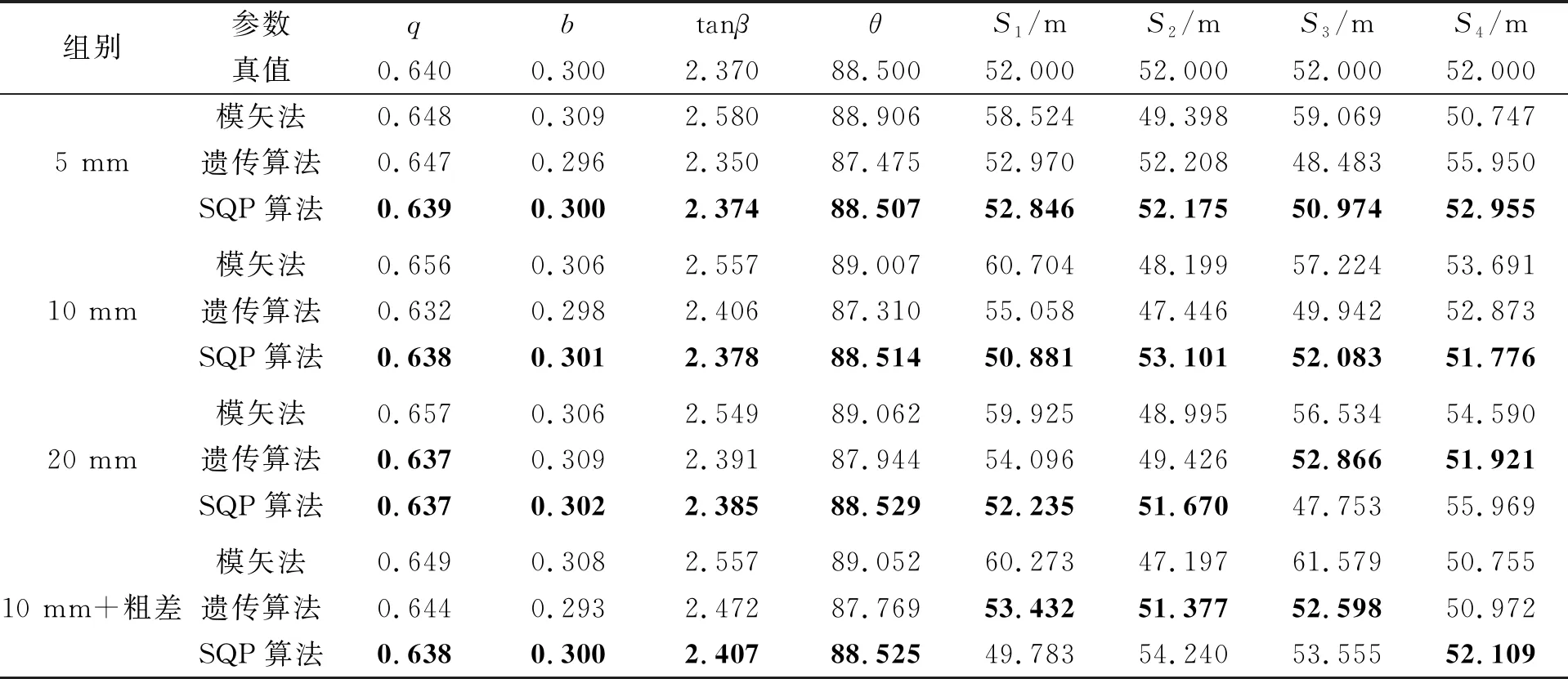
表2 SQP算法、模矢法与遗传算法反演参数计算结果

表2给出了不同组别的仿真实验，分析反演参数的结果可知：1)在不同误差情况下，SQP算法对于q、b、tanβ和θ的反演结果并未有明显变化，且与真值相比反演结果基本一致，最大误差不超过1.2%；而对于S1、S2、S3、S4反演结果具有一定的随机性，但与真值相比最大误差仍不超过8%，仍具有一定的可靠性。2)在随机误差10 mm的基础上加入了一定数目的粗差时，SQP算法反演结果并未发生改变，与之前相比变化不超过2.8%。3)随着误差的不断增大，SQP算法、遗传算法与模矢法反演参数的整体精度随着误差的增长有所降低，但结果与真值相差不大，仍具有一定的可靠性。4)对于q、b、tanβ和θ参数的反演结果，SQP算法受误差因素影响较小，结果与模矢法和遗传算法相比，均更加靠近真值。且在5 mm误差的情况下，SQP算法优势更加明显，反演结果几乎可以认为是真值。5)对于S1、S2、S3、S4参数的反演结果，SQP算法的精度随着误差的增大而有所降低。在5 mm与10 mm随机误差的影响下，SQP算法对于S1、S2、S3、S4的反演结果均优于遗传算法与模矢法；在20 mm随机误差的影响下，SQP算法对于S1、S2的反演结果均优于模矢法与遗传算法，但对于S3、S4反演的结果精度稍差于遗传算法与模矢法；在10 mm粗差的影响下，SQP算法对于S1、S2、S3、S4的反演结果均优于模矢法，但在S1、S2、S3方向上预计结果与遗传算法相比稍差，但考虑到算法的稳健性，其仍具有一定的可靠性。6)在监测数据受到不同程度的随机误差与粗差的影响下，SQP算法反演参数的整体精度最高，遗传算法次之，而模矢法较差。因此，表2证明了SQP算法对观测数据中含有随机误差和粗差具有良好的抗干扰能力。

4 结论

通过分析常用反演参数算法存在的缺陷，提出使用SQP算法反演概率积分法模型中的参数，进行大量的仿真实验，得到如下结论：

1)SQP算法不受初始值设置影响，且反演参数的结果与真值基本一致，准确度高。

2)SQP算法对随机误差和粗差具有一定的抗干扰能力，其反演参数结果在随机误差与粗差的影响下，并未产生明显的偏差，依然可靠。

3)在不同的误差环境的影响下，SQP算法反演参数的精度基本高于模矢法与遗传算法，但在少数情况下，个别方向上的拐点偏移距的预测精度可能稍低于遗传算法，考虑到SQP算法的稳健性，其结果依然可靠。

概率积分法预测结果受参数误差与模型误差影响，本文针对如何降低参数误差影响进行了改进。但在现实矿区中，实测的下沉值和水平移动值还会受到松散层厚度、断层等其他因素影响，从而影响到模型自身精度。如何精化概率积分法的数学模型，使得函数预计曲线更符合实际的下沉曲线和水平移动曲线，值得进一步研究和探索。