基于金属加工复杂零件的体积旋压成形工艺过程分析

王婷翌，吕博铭，李宣琛，王佳琪，林肖丽

(1.西北工业大学 玛丽女王工程学院，陕西 西安 710114；2.西北工业大学 材料学院，陕西 西安 710114；3.西安建筑科技大学 材料学院，陕西 西安 710114）

1 体积旋压工艺概述

体积旋压是一种低成本高效率的成形合金盘件的新工艺，金属零件的变形通过上模向下挤压而实现（如图1a所示）。其中上模在向下进给的过程中绕距中心线一定倾角的旋转轴进行自转，且同时绕中心线进行公转，如图1b所示。

目前体积旋压工艺主要应用于旋转对称的金属零件的生产，且对径厚比大的金属零件尤为适用，如薄圆盘和大法兰盘等等。

目前国内外许多学者对利用体积旋压工艺成形普通盘件、环件进行了研究，如Lin[1]、Sudipta Chand[2]等人，但对利用体积旋压工艺成形异形盘件却很少有相关报道。

目前对此类异形盘件的制造方法主要包括粉末冶金锻造、等温锻造、超塑性成形等等，但这些工艺不但耗时长、成本高，且成型外形局限性较大，因此寻找高效省时的新成形工艺有着重要的意义。

2 工艺过程研究

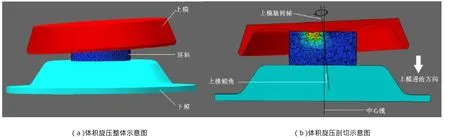
图1

本节将对同一工序中的等效塑性应变的变化行为进行分析研究，进而推进对体积旋压工艺的了解。在本次研究的工艺道次中，金属零件为一100＊200mm的GH4169圆柱型材（划分为4954个单元尺寸为15mm的四面体），上模倾角γ取值为3°，上模向下进给速度为5mm/s，上模旋转速度为180rad/min，坯料温度为1060℃。工序总用时21.6s，1s～19.45s为上模向下进给挤压阶段，19.45s～21.6s为无进给修饰阶段。

最终成型的异形盘件如图2所示：

图2 金属材料成型件示意图

图3为不同工况下零件的等效塑性应变分布云图，通过该图可以看出，等效塑性应变数值的大小的分布以及动态变化与上模的物理形态以及运动轨迹相吻合。且应变状态在零件中分布较均匀且变化较平滑，无明显应超力集中点和明显缺陷。

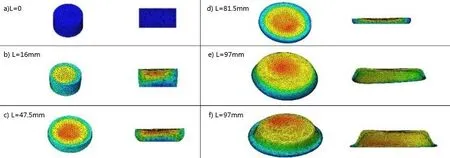
图3 不同工况下零件中等效塑性应变分布的彩色云图

图4 追踪点示意图

为方便研究，本工序插入了不同横向深度与纵向深度的九个追踪点，如图4所示。

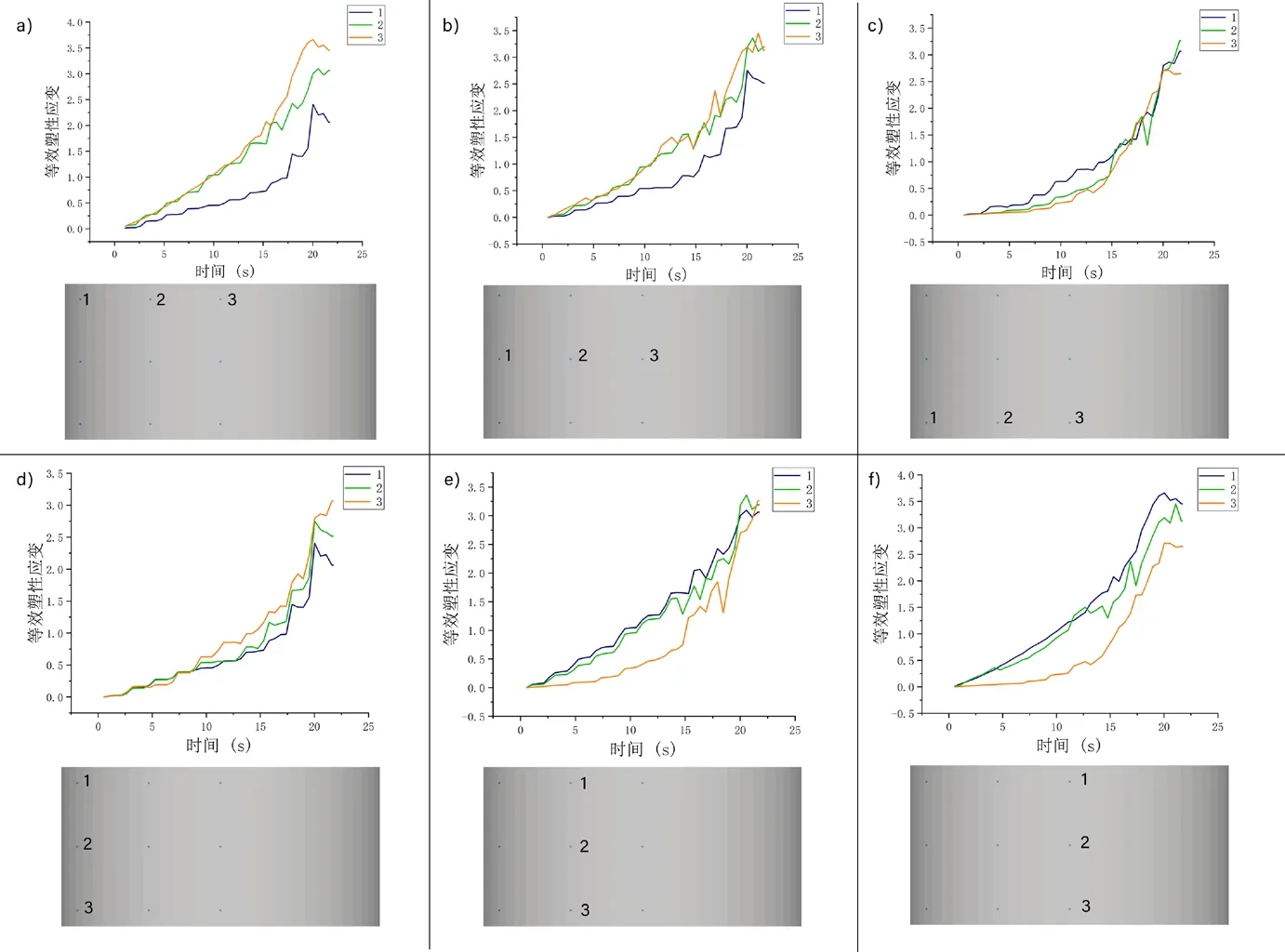
图5 体积旋压过程中各点等效塑性应变数值变化

从图5各图的总趋势可以看出，随着上模进给行程的增加，金属材料中各点的等效塑性应变都在不断地增大，且通过观察初期曲线的各峰值位置，可算出上模绕中心线公转一周的周期。图5a-c中各图的三点位于工件同一深度，通过图5a可以看出在体积旋压工艺过程中，金属材料近上表面部分同一深度各点的等效塑性应变数值从各面圆心向圆周递减；通过图5b可看出，金属材料近中部同一深度各点的等效塑性应变数值从各面圆心向圆周依旧递减，但两点之间的应变数值差较上表面部分有所减小；通过图5c可看出，材料近下表面部分同一深度各点的等效塑性应变数值从各面圆心向圆周递增。故可以推测，在体积旋压过程中，存在一深度x（x∈（50,90））使得：①在深度为0到x的各水平面上，等效塑性应变数值由圆心向圆周递减，且随着深度的增加，两点之间的数值差逐渐减小。②在深度为x的水平面上，各点的等效塑性应变数值近似相等。③在深度为x到100的各水平面上，等效塑性应变数值由圆心向圆周递增，且随着深度的增加，两点之间的数值差逐渐增大。且综合三张图可得出在体积旋压过程中，深度较小的各点的等效塑性应变数值大于深度较大各点的数值[3]。

图5d-f中各图的三点位于工件同一半径，通过图5d可以看出，金属材料中近外围各点的等效塑性应变数值随深度的增大而增大；通过图5e与f可以看出，金属材料中中等半径的各点与中心轴上的个、各点的等效塑性应变数值随深度的增大而减小。故可以推测，在体积旋压过程中，存在一半径y（y∈（45,90））使得：①在半径为0到y的各圆柱面上，各点的等效塑性应变数值随深度的增大而减小，且随着半径的增大，两点之间的数值差逐渐减小。②在半径为y的圆柱面上，各点的等效塑性应变数值近似相等。③在半径为y到100的各个圆柱面上，等效塑性应变数值随深度的增大而增大，且随着半径的增加，两点之间的数值差逐渐增大。且综合三张图可得出在体积旋压过程中，半径较小的各点的等效塑性应变数值大于深度较大各点的数值。

3 结语

体积旋压成型工艺是一个综合了多因素的复杂的成型过程，利用三维有限元模型可以对该工艺进行很好的模拟与研究。通过本次的模拟，揭示了复杂金属零件的体积旋压成型过程是一个数次小应变积累成最终应变的塑性成形工艺，应变云图中应变的分布表现出由上表面到下表面的传递特性，从而产生径向与轴向的变形不均匀而周向变形相对均匀。且总的来说近中心轴面的近上表面区域的等效塑性应变较大，而近外表面的近下表面区域应变量较小。

本文对体积旋压成型的规律进行的一定研究，可为进一步认识体积旋压工艺机理和探究最优工艺路径提供了有价值的经验。