钢-高强混凝土组合梁收缩的计算分析
2020-05-15章胜平1楚秀娟彭祖强马江鸿
章胜平1,陈 旭,楚秀娟 1,彭祖强,马江鸿
(1.昆明理工大学 建筑工程学院,云南 昆明 650504; 2.昆明学院 城乡建设与工程管理学院,云南 昆明 650214)
收缩是混凝土开裂主要诱因之一。作为永久作用,收缩在荷载的每一组合中都应当被考虑。素混凝土收缩受到时间、混凝土组成、环境湿度等的影响,结构中混凝土收缩还受到徐变、钢筋和超静定支座等约束的影响。这些因素多而复杂,使收缩效应计算具有复杂性。高强混凝土应用越来越多,强度提高的同时伴随了脆性更大、延性更差、更容易开裂等问题。高强和普通混凝土收缩徐变在本质上有较大的差别[1-3],欧洲FIB国际混凝土联合会所发布的混凝土模式规范(MC2010)[4]对此进行了重大修正,我国2018公路桥规[5]仍然基于MC1990模型[6],对高强混凝土收缩徐变给出了与混凝土强度标准值成反比关系的相同的折减系数。
组合梁翼板收缩将引起混凝土开裂、钢梁翼缘局部失稳、跨中下挠增加和超静定支座负弯矩增加等不利影响[7-8],这些是设计中必须考虑的[9]。采用高强混凝土,这些不利影响会有怎样的变化?采用MC2010和MC1990在结果上有怎样的不同?本文按照全截面法,基于有效模量比推演了组合梁收缩自应力、挠度和收缩次弯矩的计算公式,通过算例对各种收缩效应进行了参数分析。以期对我国规范的修编提供理论依据。
1 计算公式的推导
1.1 收缩自应力和挠度
从初凝开始,因水化反应和干燥,混凝土中的水分会不断地减少,使得混凝土的体积也在不断地减小,该变化为收缩。混凝土翼板收缩相当于发生在组合梁内部的强制变形,受到钢梁约束,在截面上产生随时间变化的收缩自应力,混凝土在自应力作用下又将产生弹性应变和徐变,则收缩必然耦合了徐变。在欧规4(桥梁)[10],采用有效模量比(nL)来考虑收缩自应力的徐变,将混凝土的面积(Ac)和惯性矩(Ic)换算为等效钢在龄期t的换算面积(Act)和惯性矩(Ict),计算式为:
(1)
式中:Es和Ec分别为钢和混凝土的弹性模量,ψL为徐变因子(收缩作用ψL=0.55),φ(t,t0)为徐变系数,t0为加载龄期。
对收缩自应力,普遍采用的是三阶段叠加法[11],即:a.假想翼板和钢梁之间没有联系,翼板自由收缩;b.虚拟收缩力将翼板拉回;c.翼板和钢梁结合,释放收缩力,组合截面承受回弹力。
本研究将补充另一种简单方法(结果相同),无需假想先分离后结合,以组合截面为研究对象,以部分截面(混凝土翼板和钢梁)的内力为未知量,按照平衡和变形协调方程,推演应力的计算式。
部分截面内力在各自重心轴产生轴向应变和曲率,如图1所示。其中选择混凝土翼板重心(C)作为任意参考轴(z),优点是无论混凝土的面积随时间怎样退化,重心位置不会改变,静距为零。

注:zt为组合截面重心(V)的坐标;ysc为部分截面重心之间的距离;yc为混凝土翼板的高度;ys1和ys2分别为钢梁重心(S)与其上、下边缘的距离;Mct和Nct为混凝土翼板在龄期t的弯矩和轴力;Mst和-Nct为钢梁在龄期t的弯矩和轴力;As和Is为钢梁的面积和惯性矩
图1 收缩引起的截面变形
Figure 1 Section deformation caused by shrinkage
按照收缩自应力的平衡条件,有:
Mst+Mct=rNct
(2)
按照应变和曲率的变形协调条件,有:
(3)
联立式(2)和式(3),解得:
(4)
式中:Nsh(=EsActεsh)为虚拟收缩力,It为组合截面在龄期t的等效钢的换算惯性矩,It和zt的计算式为:
(5)
混凝土翼板和钢梁在各自重心的应力分别为:
(6)
混凝土翼板上(下)边缘应力σc1t(σc2t)和钢梁上(下)边缘应力σs1t(σs2t)的计算式为:
(7)
钢梁的弯曲刚度不因时间改变,故用Mst计算组合梁的挠度。对简支组合梁,收缩所引起的Mst在长度方向为常量,假设跨度为l,则挠度为:
(8)
1.2 收缩次弯矩
连续梁在各跨徐变特性相同或者跨度相同时,持续荷载徐变产生的次弯矩为零[12],仅有收缩作用产生的次弯矩。以两等跨连续组合梁为研究对象不失一般性,按照中间支座的转角协调条件,建立收缩作用下次弯矩Msh的力法方程,有:
δ11,tMsh+Δsh=0
(9)
式中:δ11,t为基本体系在龄期t的柔度系数,Δsh为收缩作用下基本体系在次弯矩方向的相对转角,计算式分别为:
(10)
式中:I0为组合截面在初始龄期t0的等效钢的换算惯性矩。
将式(10)代入式(9)有:
(11)
由式(11)可知,等跨连续梁的次弯矩与跨度无关,只与截面参数有关。
2 收缩应变和徐变系数
从前面的分析可知,收缩引起的自应力随着时间进程还将引起混凝土的徐变,其计算关键是合理地选择收缩应变和徐变系数模型。新版MC2010模型相比之前MC1990的有重大变化,原因是MC1990模型不适用于高强混凝土。
2.1 收缩应变
MC1990模型表示为混凝土强度影响因子(εs)、环境相对湿度影响因子(βRH)和时间发展方程(βs,同时考虑有效厚度)的积形式。在干燥开始龄期ts后的龄期t,收缩量εsh(t,ts)为:
εsh(t,ts)=εs·βRH·βs
(12)
其中,混凝土强度fcm影响因子εs的计算式为:
εs=[160+10βsc(9-0.1fcm)]·10-6
(13)
实验结果表明,收缩可以分为自收缩和干燥收缩两个部分,MC1990将自收缩和干燥收缩表示为同一规律的单一模型。自收缩产生于混凝土的水化和硬化过程,与外界没有水分交换,大部分可在几个月内完成,主要取决于混凝土强度。干燥收缩产生于水分的迁移,与环境湿度、有效厚度和混凝土组成等有关,大部分要在几年内完成。普通混凝土的自收缩小(小于5%),可被忽略,因此尽管在形成MC1990模型时,已经认知了自收缩和干燥收缩本质上的区别,MC1990仍然采用了单一模型。
高强混凝土自收缩大,甚至可以超过干燥收缩,在计算中不能被忽略。鉴于高强混凝土应用越来越多,MC2010将收缩分解为自收缩(基本收缩)和干燥收缩两项之和,表示为:
(14)
式中:εa和εd分别为混凝土强度fcm对自收缩和干燥收缩的影响因子;βa(t)和βd(t-ts)分别为自收缩和干燥收缩的时间发展方程,后者同时考虑了有效厚度h的影响;环境湿度影响因子βRH也考虑了混凝土强度的影响。
骨料、水灰比和水泥浆等组成是收缩的直接影响因素,如大量粗骨料显著减小收缩。混凝土强度能综合反映这些组成的影响,它对自收缩和干燥收缩的影响规律不同,如自收缩与水灰比成反比,与水泥浆数量成正比,干燥收缩与水灰比和水泥浆数量成正比。高强混凝土水灰比小,活性掺和料和外加剂多而自收缩大,因此MC2010模型将混凝土强度因子计算式对自收缩和干燥收缩分开,调整为:
(15)
式中:下标“a”和“d”分别表示自收缩和干燥收缩,αa、αd1和αd2分别为水泥品种对自收缩和干燥收缩的影响系数。
比较高强和普通混凝土的收缩值,显著不同的是自收缩和干燥收缩之间的比例关系。如,当结构暴露于室外潮湿环境时(RH=80%),50 a后收缩总量几乎相同,约为0.35‰~0.4‰,对C20混凝土自收缩约为总量的7%,对C100显著地增大至约53%[1]。虽然自收缩均匀地发生在混凝土的内部,不会产生干燥收缩因不均匀分布所导致的自应力。但须注意的是,自收缩是混凝土由始至终发生的体积缩小,早龄期混凝土抗拉强度低,高强混凝土自收缩大意味着早期开裂风险大。
MC2010模型表示为自收缩和干燥收缩的和形式,对混凝土强度影响因子公式进行了大调整,修正了MC1990模型低估高强混凝土收缩的不足,提高了高强混凝土收缩的预测精度。
2.2 徐变系数模型
MC1990徐变系数模型为积形式,即:
φ(t,t0)=φRH·β(fcm)·β(t0)·βc(t-t0)
(16)

与收缩相似,MC1990模型在混凝土强度因子上的单一模型也不能合理反映普通和高强混凝土的变形特性,造成了对低强混凝土徐变的低估,对高强混凝土徐变的高估[13]。
MC2010模型按照基本徐变和干燥徐变,将徐变系数修正为和形式,即:
(17)
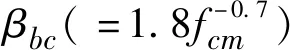
基于实验结果,MC2010模型在基本徐变的时间发展方程用对数函数,在干燥徐变用双曲幂函数,修正了MC1990的单一双曲幂函数的时间模型。
2.3 2018公路桥规的收缩徐变计算

3 组合梁收缩的计算分析
3.1 收缩应变和徐变系数
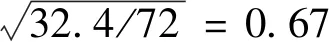

表1 收缩和徐变系数Table1 Shrinkageandcreepcoefficient普通混凝土fcm=30MPa高强混凝土fcm=80MPaMC2010-0.34‰-0.33‰收缩MC1990-0.29‰-0.13‰2018桥规-0.29‰-0.09‰MC20102.351.02徐变系数MC19902.221.362018桥规2.220.91 注:RH=80%;ts=3d;t0=3d;t=3a;αas=700;αds1=4;αds2=0.12;有效厚度h=11.5cm。
a.从表1 MC2010数据可见,在收缩和徐变上,高强和普通混凝土的时随规律表现完全不同。在收缩上,高强和普通混凝土数值几乎相同。而在徐变上,高强比普通混凝土小很多。所以我国2018公路桥规对高强混凝土收缩和徐变采用相同的折减系数,将造成收缩计算的很大偏差。
b.比较MC2010和MC1990,MC1990远远低估了高强混凝土的收缩,在徐变系数上高估了高强混凝土的徐变,低估了普通混凝土的徐变。我国2018公路桥规基于MC1990的折减系数法并不能体现MC2010模型的优点,反而更显著地低估了高强混凝土的收缩。若仍然基于MC1990模型,在高强混凝土收缩上应当要乘以一个较大的扩大系数,而不是折减系数,如本算例的扩大系数为2.54。
3.2 截面参数的时间变化
收缩使混凝土翼板轴向压应变增加,曲率增加,可等效为对弹性模量的退化,通常用假想的有效模量表示。对换算截面,这相当于改变了混凝土翼板的等效钢面积、惯性矩等截面参数。按照式(1),计算组合截面在收缩前和3 a后的截面参数见表2。

表2 截面参数Table2 Sectionparameters类别nsh收缩前收缩后普通混凝土MC2010MC1990高强混凝土MC2010MC1990716.0515.5410.9212.23Act/cm2Ict/cm4zt/cmIt/cm4750039100035.155.93×106467.412434457.734.68×106482.512513056.824.73×106686.773576946.815.28×106613.1431935505.1×106 注:Es=210GPa;ψL=0.55;Ec=30GPa;bc=300cm;yc=25cm;As=472.8cm2;Is=1.55×106cm4;ysc=114.8cm;ys1=102.3cm;ys2=47.7cm2。
由表2可见,收缩使混凝土翼板的面积和惯性矩减小,使组合截面的重心轴下移,削弱了组合截面的刚度,高强混凝土的减小程度要小于普通混凝土。换句话说,高强混凝土收缩对有效模量比的影响小于普通混凝土。但采用MC1990模型将高估高强混凝土对模量比的影响。
3.3 截面自应力的时间变化
在组合截面上,收缩所引起的自相平衡的特征应力,由于钢和混凝土在弹性模量上的不同,截面应力为如图2所示的不连续分布,其中收缩的计算时间是3 a。

图2 收缩自应力Figure 2 Eigen stress caused by shrinkage
如图2所示,混凝土翼板下部为受拉,将带来混凝土开裂的风险;由于组合截面显著不对称,型钢梁上下翼缘受到的影响显著不同,上翼缘靠近混凝土,起到了主要约束作用,压应力增加相当可观,可能导致受压失稳,而下翼缘远离混凝土,应力只有少量的增加。
从数值上看,高强与普通混凝土收缩自应力几乎相同。但采用MC1990模型显著低估了高强混凝土的收缩自应力,由此低估钢筋用量将可能导致混凝土开裂。
3.4 简支梁挠度的时间变化
即便没有横向荷载,单独的收缩可引起简支梁的显著下挠,因组合截面的显著不对称。假设简支组合梁跨度为30 m,按照式(8)计算收缩3 a后的挠度,见图3。

图3 简支梁的挠度Figure 3 Deflection of simply supported beam
如图3所示,高强与普通混凝土挠度几乎相同。但采用MC1990模型将显著低估了高强混凝土的挠度。
3.5 连续梁次弯矩的时间变化
收缩引起的次弯矩过大,是导致组合梁负弯矩区混凝土翼板开裂的主要原因之一。按照式(11),计算两等跨连续组合梁的中间支点次弯矩与时间的关系,见图4。

图4 次弯矩Figure 4 Secondary moment
如图4所示,无论是高强还是普通混凝土,收缩次弯矩在数值上都较大,不能被忽略,高强混凝土的略低于普通混凝土。但采用MC1990模型显著低估了高强混凝土的收缩次弯矩,由此低估钢筋用量将可能导致混凝土开裂。
4 结论
与普通混凝土相比,高强混凝土在水灰比、活性掺和料和外加剂等组成上显著不同,使它们在收缩徐变的时随规律上有本质的区别。针对高强混凝土应用越来越多,欧洲混凝土模式规范(MC2010)的收缩徐变模型进行了大修正。组合梁截面显著不对称,收缩作用产生的应力、挠度和次弯矩较大,当应力超过混凝土抗拉强度,混凝土就要开裂,引起工程结构的使用和安全问题。对高强和普通混凝土的收缩徐变模型进行比较,分析它们对组合梁收缩效应的影响,得出以下结论。
a.高强和普通混凝土在收缩值上差别不大,而MC1990模型低估了高强混凝土的收缩。高强混凝土的徐变系数显著低于普通混凝土,而MC1990模型高估了高强混凝土的徐变系数,低估了低强度混凝土的徐变系数。我国2018公路桥规采用的仍然是MC1990模型,对C50以上混凝土收缩徐变乘以了一个完全相同的折减系数,更加显著地低估了高强混凝土的收缩(对收缩应当乘以扩大系数),没有反映和体现MC2010模型的水平和优点。
b.对简支组合梁的收缩自应力和挠度,高强和普通混凝土在数值上差别不大。对连续组合梁的收缩次弯矩,采用高强混凝土的结果小于普通混凝土的。采用MC1990模型将显著低估了这些收缩效应,可能造成安全隐患。
