AK-MCS中初始设计样本数量对可靠度计算的影响分析
2020-05-14赵少飞胡欣宇邢明源
谢 娟,赵少飞,胡欣宇,邢明源
(华北科技学院 建筑工程学院, 北京 东燕郊 065201)
0 引言
近几年来,AK-MCS方法由于采用较少的样本数量能够高效地评估失效概率的优势,而在土木工程可靠度分析中越来越受到关注[1-5],但在以往的研究中,基于AK-MCS方法进行可靠度分析时,仅选取较少初始样本数量来计算对应的响应值,进而建立Kriging模型进行可靠度计算。研究初始样本数量的选取对可靠度计算精度的影响还没有文献报道。Jiang等[6]建议初始样本数量与随机变量个数的关系按照经验取值。谢延敏等[7]在其基于Kriging法计算可靠度分析中提到,Kriging预测值与函数精确值之间的误差,主要取决于初始样本实验设计(DOE),即初始样本数量及抽取方法,而与Kriging模型的函数类型关系不大。孙志礼等[8]在其可靠度分析研究中指出,初始样本在Kriging模型的预测过程中发挥着重要的作用,并对功能函数预测精度具有一定的影响。若初始样本数量较少会影响初始Kriging模型的预测精度,而数量较多又可能在主动学习时增加样本数量的调用次数。故研究选取适当的初始样本数量对AK-MCS方法评估失效概率精读具有重要的意义,在土木工程中,由于功能函数往往较为复杂,在进行可靠度分析时,计算本身需要相对大的工作量,如果找出初始样本数量对计算可靠度精读的影响规律,将能有效的提高计算效率,这对工程可靠度分析具有重要的意义。
在土木工程的可靠度分析中,研究的随机变量很多情况下为2个[3,9,10],本文围绕随机变量为2个时不同初始样数量对失效概率评估精度的影响,并进行对比分析与案例验算。
1 AK-MCS方法
AK-MCS方法是将Kriging与Monte Carlo结合的一种主动学习方法,该方法能够对接近极限状态的点进行评估,从而提高初始kriging模型的预测精度,最重要的是,它能够将注意力集中在概率密度足够高的点上,从而对失败概率产生显著影响。该方法同时给出了失效概率及其变异系数的Kriging估计,利用学习函数寻找下一个最佳样本点从而进行评估,而不需要对整个Monte Carlo总体进行繁琐的估计,这种学习方法进行的模型评估精度较高,而且大大降低了迭代次数。但这种方法研究可靠度时主动学习的效率取决于学习函数的选取,Echard等[4]在提出这种方法时表明U函数更适合作为AK-MCS方法的学习函数进行主动学习,故本文选用U函数作为主动学习函数进行研究,AK-MCS方法基本步骤如下[4]:
(1) 基于随机变量的分布生成NMC个随机样本,用SMC表示,称为候选样本点,候选样本只有在主动学习时才计算功能函数。
(2) 利用拉丁超立方法进行实验设计,生成初始的N1个样本点,分别选取随机变量的2倍、3倍、4倍、5倍数量的试验样本点进行研究。这些样本点用SDoE表示。
(3) 利用SDoE和实际功能函数计算响应值,用YDoE表示。基于SDoE和YDoE利用MATLAB软件的DACE工具箱建立Kriging预测模型,并利用工具箱中的预测函数估计候选样本总体SMC所有样本点的预测值和方差。最后利用公式(1)(2)分别计算其失效概率Pf和变异系数COV(Pf)。
(1)
(2)
(4) 根据公式(3)计算出总体SMC中所有样本点对应的学习函数值U(xi)值。
(3)
(5) 根据学习停止条件选择下一个最佳样本点,即U(xi)值最小值对应的样本点,这是因为U(xi)越小,就可能有两种情况出现,一种是在这一点上的预测方差较大,另一种是这一点的预测值很小,即这一点有极大的可能接近极限状态面,若将这一点加入样本,将会提高Kriging模型的预测精度,故将这一样本点定义为下一个最佳样本点,将最佳样本点加入初始样本点中,重复步骤(3)(4),直到Umin≥2停止学习。
(6) 根据式(1)和式(2),利用最终的Kriging预测模型计算失效概率Pf和变异系数COV(Pf)。如果变异系数COV(Pf)≤5%,主动学习停止,认为结果可以接受。如果不满足,则增加Monte Carlo候选样本的数量,转到步骤(3)计算,直到满足条件。流程图如图1所示。
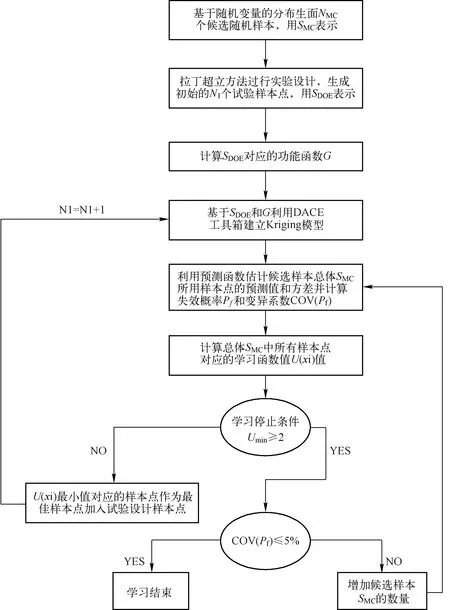
图1 AK-MCS法计算流程图
2 算例分析
为了分析AK-MCS方法中初始样本点数量变化计算结果的影响,通过一个岩土边坡算例[7]进行对比分析,并结合一个结构可靠度功能函数算例[1]进行了验证。
2.1 算例
选取文献[11]中一边坡示例,黏聚力c和摩擦角φ为随机变量,2个随机变量独立且服从正态分布。其他变量为确定性参数。功能函数化解结果如下式。随机变量分布如表1。

G(c,φ)=5c+tanφ-1 (4)
为了进行对比研究,利用Monte Carlo法,进行104次抽样计算其失效概率作为对比研究的基准。根据DACE算法[12]编制MATLAB程序,首先利用拉丁超立方法选择随机变量的2倍、3倍、4倍、5倍,即4、6、8、10个初始样本点,分别建立Kriging模型,进行主动学习,直到达到学习停止条件。为了更好的反应主动学习过程中,初始样本点和增加样本对计算结果的影响,分别建立4种条件下增加样本点数与Pf和学习函数最小值Umin的关系图,如图2所示。
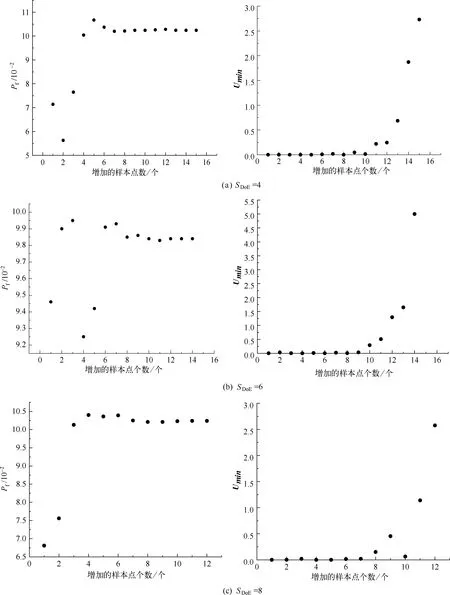
图2 Pf和Umin与增加样本点个数的关系
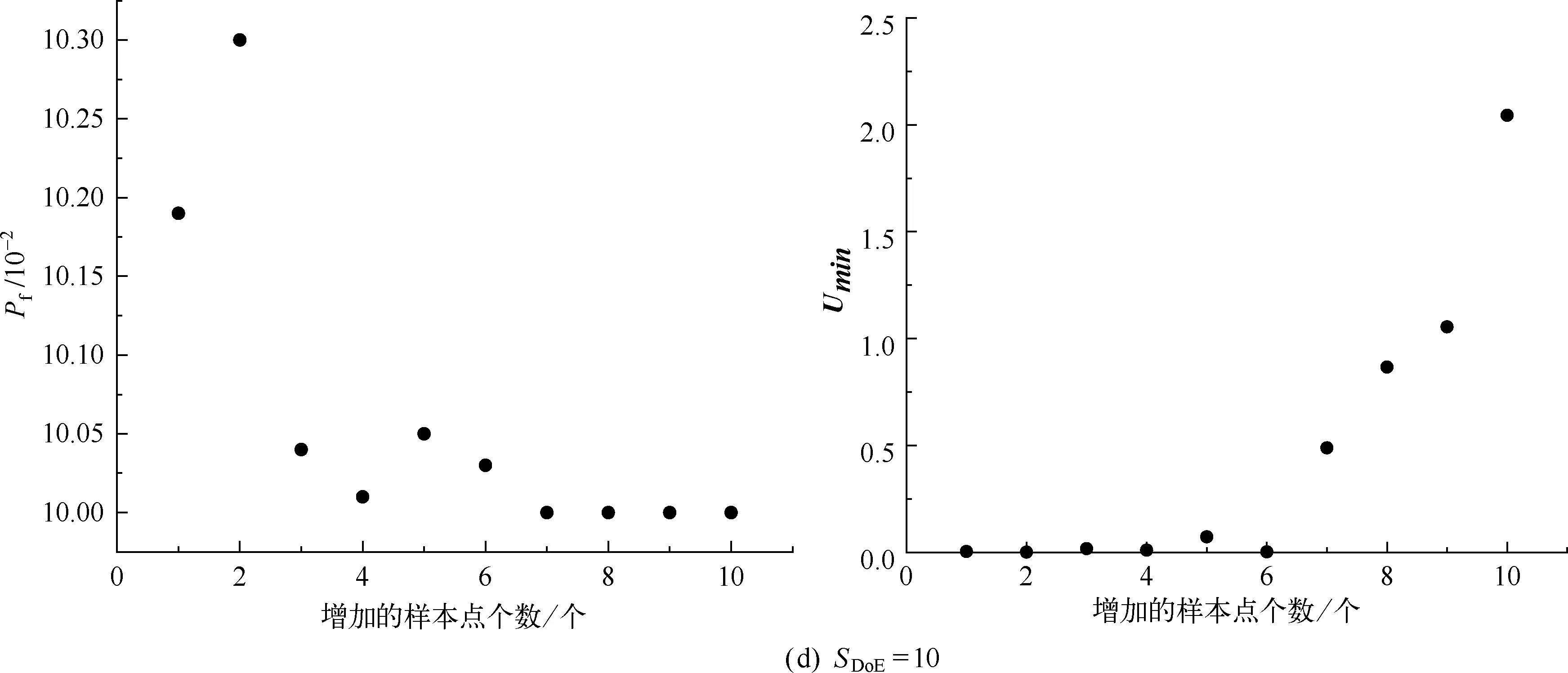
图2 Pf和Umin与增加样本点个数的关系(续)
由图2可以看出,样本点增加到一定个数时,失效概率的值趋于收敛,同时学习函数最小值趋于大于2,这就意味着预测结果趋于稳定,但是当初始样本点的数量为随机变量的2倍、3倍、4倍时,学习第一次的失效概率,这里定义为初始失效概率,与学习停止后的失效概率相差较大,也就是说初始样本点的数量选用这三种数量时,对初始的Kriging模型的预测精度相对不高,而初始样本点的数量为随机变量的5倍时,初始的失效概率与最终的失效概率相差较较小,具体的精度对比结果如表2所示。可以定量看出当初始样本点为随机变量的5倍时,初始的失效概率与最终的失效概率相对误差最小,这也说明这个条件下将对初始模型的拟合具有较好的精度。

表2 初始失效概率与最终失效概率的对比图
将4种状况下的失效概率与Monte Carlo模拟的结果进行对比,对比结果如表3所示。
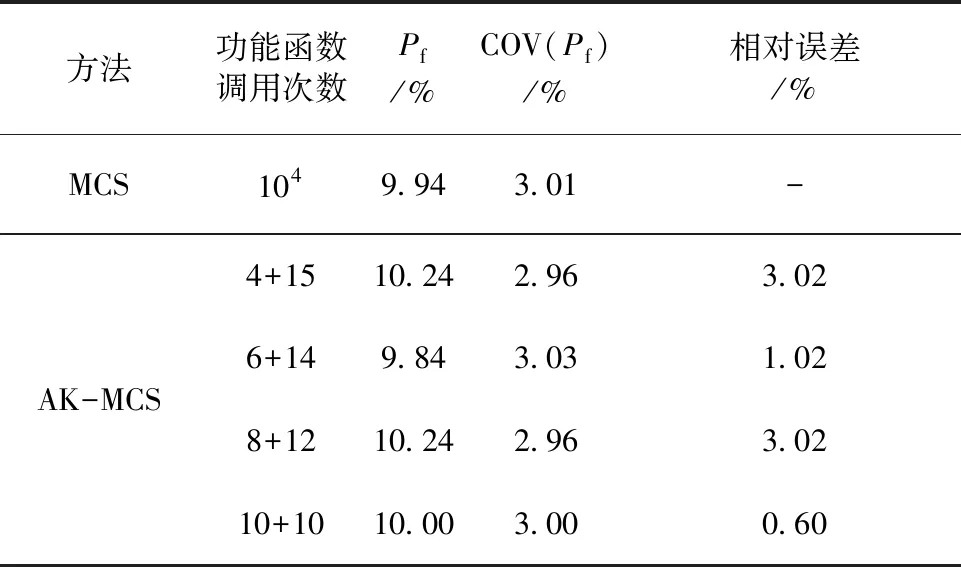
表3 算例计算结果
由对比数据可知,选取的初始样本点的多少对需要总样本点的数量影响不大,也就是对功能函数调用次数影响不大,基本相同,但不同的初始样本点计算失效概率需要增加的样本点个数不同,较小的初始样本点需要的增加的样本点相对较多,同时也对评估失效概率的精度具有一定的影响,当初始样本点取10个即随机变量的5倍的时候,失效概率的评估精度最高。针对以上研究结论,进行一下算例验证。
2.2 验算算例
该案例选自文献[1]中某结构功能函数,随机变量为2个,其表达式为:
G(x1,x2)=x1x2-1500
(5)
式中,随机变量x1、x2相互独立且均服从正态分布,随即变量取值如表4所示。

表4 验证算例中随机变量分布表
根据算例的计算步骤,验证算例4种情况下计算结果见表5。
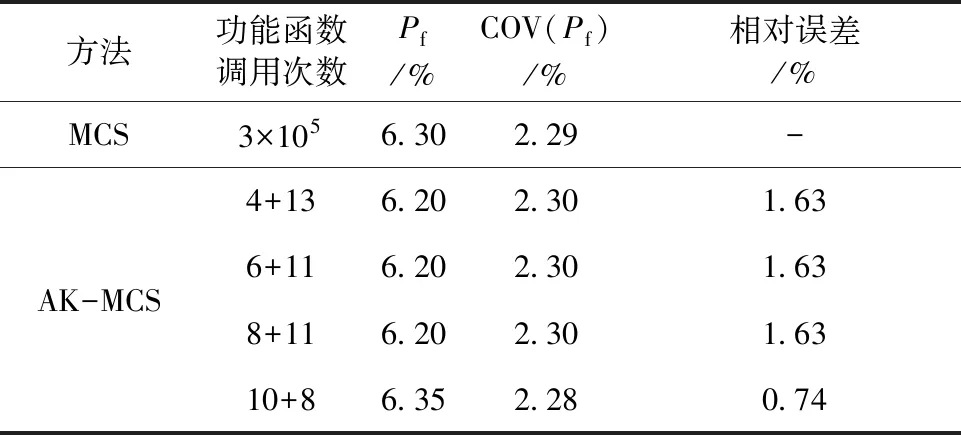
表5 验证算例计算结果
由对比可见,四种状况下功能函数调用次数相近,但失效概率的评估精度不相同,仍然是初始设计样本点个数为随机变量的5倍时,失效概率的评估精度最高。可见以上研究分析结果正确。
3 结论
针对2个随机变量的功能函数进行可靠度分析,计算其失效概率。利用MATLAB中DACE工具箱分别建立四种抽样数量情况下的Kriging模型,对比分析失效概率计算结果,得出以下结论:
(1) 初始样本数量对失效概率的评估精度有较大的影响,对于2个随机变量的功能函数,初始设计样本数量为随机变量的5倍时,AK-MCS法评估的失效概率几乎与Monte Carlo的失效概率相同,精度最高。
(2) 初始样本数目差异对主动学习需要增加的样本数目有一定影响,较少的设计点需要主动学习的次数较多,而对功能函数的调用次数改变不大。
