基于时间标签的公交运营时段划分方法
2020-05-14向一擘ZHANGJinXIANGYibo
张 瑾,向一擘 ZHANG Jin, XIANG Yibo
(昆明理工大学 交通工程学院,云南 昆明650000)
(School of Transportation and Engineering, Kunming University of Science and Technology, Kunming 650000, China)
0 引 言
随着城市机动化出行的发展,各大城市机动车保有量不断增多,同时人民日益强烈且多样化的出行需求也使得交通负荷越发加重,给城市交通带来日益严峻的考验。地面常规公交作为“高效率、低成本、大运能”城市公共交通的代表,是政府用于解决交通需求及交通拥堵问题的强力手段。随着轨道交通的兴起,目前认为地面常规公交的交通出行占比已被地铁和小轿车所瓜分,但国家统计局信息表明,地面常规公交仍是城市交通出行的主力,在公共交通占有较大比例(如表1 所示)。因此,对地面常规公交的研究仍是解决城市交通问题的可靠途经。

表1 各城市交通方式出行量占比表
为了改善地面常规公交服务水平,必须对公交运营情况进行全面了解。而公交线路在不同的运营时段,其运营时间和客流规律往往存在很大差异。所以必须将公交运营时段进行划分来掌握不同情况下的公交运营规律。针对这方面的研究,杨新苗[1]等依据利用有序样品聚类的费歇算法完成运营时段划分;沈吟东[2]等采用改进的K-means 聚类算法划分时段;尚春琳[3]等研究了基于公交优先的交叉口多时段划分方法;靳文舟[4]等提出基于最小化车队运营时段成本的划分方法;张雪妍[5]等采用Fisher 有序聚类算法完成了划分时段仿真。
在当前,公交企业主要仍是通过经验人工完成时段划分,而随着车内GPS 定位系统的普及,公交企业在获取大量数据储备的同时,如何利用这些大规模数据完成公交运营时段划分显得尤为重要。本文基于GPS 数据,参考K-means 算法具有解决大规模数据聚类的能力,设计相对应的算法以期自动化、高效率、高精确度的实现公交运营时段划分,为分时段公交运营研究打下基础。
1 公交运营时段划分方法
当前对公交时段划分主要以客流量作为依据,常用的通过乘客数量对公交调度划分忽略了外部客观环境对公交派车数量的限制,常有如下情况:线路乘客出行需求旺盛,但由于当前整个线路断面客流量较大,增添派车不能及时到达目标站点,造成串车等现象,既造成了运力浪费,也增加了交通负荷。也有学者使用线路单程时间作为划分依据,但由于每一个数据代表的时间段较长,不能反映实时的公交乘车需求。
本文使用公交于站间运行所花时间作为分类依据。可以认为该指标既反映了乘客出行需求,当公交站间运行时间短时,当前线路交通状况良好,也代表当前时段居民出行欲望不强,公交使用者数量也相应减少;而当公交站间运行时间较长时,则与前种情况相反,可以认为公交出行需求旺盛。
对于时间段的不同,公交所处道路交通状况也有所不同,进而导致运行时间产生较大差异。目前,公交运营企业对于车辆运行时刻表的编制往往不注重道路交通状况的变化,同时调度计划也不考虑各个站点的实时状况,往往采用“一刀切”的手法,也因此导致“串车、车辆同时滞站”等乱象发生。
考虑到本文以车辆于站点间运行的时间作为时间段划分依据,产生的数据量较多,因此拟采用定量的方法,以在地球科学、信息技术、交通运输等方面获得广泛应用的K-means 算法为基础设计算法。
1.1 运营时段划分方法
传统的K-means 算法的基本思路是:设有K个簇,依据选定的距离测度方法,将一系列单元逐个赋予或重新赋予最“接近”的簇,并反复迭代,直至满足预设的终止条件。
首先要求人为制定的簇的个数K,随机于元素集合P中选取K个基本元素作为簇的中心。然后遍历所有元素,计算元素与各个簇中心的距离,并将其划分至最近的簇中心。初次完成后,记录整个集合中各元素与簇中心的距离之和,并按照改进中心规则选取新的簇中心,之后重复上述过程,反复迭代至满足停止条件。
1.2 划分方法改进
使用经典K-means 算法虽然可以获得公交运行时段划分的结果,但针对公交运营特点可以对部分算法内容做出改进,以减少运算时间。
改进规则1:初始簇中心的选择。公交运营不同时段是具有明显的时间距离的,因此最终所获得的各个簇中心必定彼此有一定距离。而K-means 算法随机产生各个初始簇中心,该过程可能使多个簇中心点集中于一处,迭代过程会花费较多的时间来获得最优解。因此本文基于GPS 数据自带的时间标记为依据,提出改进的初始簇中心生成方法。公交GPS 数据示意如表2 所示:

表2 公交GPS 数据示意表
根据整体元素集时间范围[Ta,Tb],每个元素p均有其相应的时间标记Tp。首先根据目标簇数K,计算平均时间间隔t= Tb-Ta/K。随机生成1 号簇中心m1,对m1的时间标签Tm1向正、反方向检验,判断是否有下式成立:
正方向:Tm2=Tm1+t∈[Ta,Tb]
反方向:Tm3=Tm1-t∈[Ta,Tb]
若正方向的检验成立,则将TC2作为2 号簇中心的时间标签,否则中断该方向上判断;反方向的判断于此相同。反复迭代该过程直至完成K个初始簇中心时间标签的选取,再从拥有簇中心标签的元素中随机选择簇中心点。
改进规则2:不必要距离计算。在将元素划分进各个簇的过程中,需要计算元素与每个簇中心的距离并划分至最近的簇。而在本文研究问题中,每个公交时段均具有明显的时间范围,即具有较强的时间相关性。
为减少元素归类这一过程的计算量,本文将各个簇中心按其时间标签进行由小至大排序,依次计算元素时间标记Tp与各个簇中心时间标记Tm的距离,若出现Tp-Tmi>Tp-Tmj,K≥j>i≥1,则停止元素p的计算并将其划分至簇Ci。
改进规则3:边界元素的划分。各个簇的边界元素由于其处于两个公交运营时段的过渡位置,包含两个时间段的信息,若简单通过距离进行划分难以保证其科学合理性。本文引入决策变量ε,通过以下算法完成边界元素的划分。
对于边界元素p,判断其与最近两簇中心的距离,若则表明该元素与最近、次近簇中心的距离差别明显,可将其归类至最近的簇。若2p-mi-mj<ε,则将该元素归类至待定集合φ,并寻找与该元素最近的元素pc1。若pc1属于簇Ci且
基于上述改进,本文公交时段划分方法如下:假设一个已知的公交站间运营数据集合P,则其中每一个车辆站间运营时间归一化后的数据为基本单元p,p∈P。簇的个数K可以根据公交运营计划确定,其中每个簇为如“低峰—早高峰—平峰—晚高峰—低峰”的交通状况可以拟定K=5。簇中心mi迭代时通过簇内单元位置,即簇内所有车辆站间运营时间的平均来确定新的簇中心单元间距离的度量采用欧几里得距离进行度量。采用作为聚类效果的目标函数。
2 实例验证
以某日昆明市5 路公交车6:00~18:00 运行的GPS 数据为例进行说明,首先,由于车辆在不同的站点间需要的运行时间不同,将车辆运行时间数据同数据集中最大值相除,进行归一化处理。其次,以1 分钟作为时间基本间隔,确定各个数据的时间标签。取ε=2,N=7 得到示意图如图1 所示:

图1 目标簇N=7 时数据示意图
由图1 可以看出,所选案例在运行12 个小时中,呈现“低峰—平峰—高峰—平峰—低峰—次高峰—低峰”的分布,符合常见的公交运营分布规律。而该线路出现上述分布特征,是由于该线路主要服务对象为老年乘客,主要的出行活动为休闲、购物、接送孩子等,出行高峰较常见的通勤高峰有所延后,因此出行高峰出现的时间标签为[21 4,318 ],既9:30~11:20,也与现有的研究相符[6]。而在经过第一个早高峰后,乘客出行欲望消减,直至时间标签[52 2,622 ],即15:30~16:30 期间,外出的老年人需要回家,也带来本组案例公交的次高峰。
依据本文提出的方法成功将公交运营时段进行划分,这是因为在计算各个元素距离的过程中,将运行时间归一化既可以消除线路站点距离不同对结果的影响,使其统一为表现交通运行状态的指标,且其上下界为[0,1 ];同时基本单位为1min 的
时间标签的引入,有效地增加了时间在欧式距离计算结果中的占比,在各元素进行簇的归类过程中时间起到更大地影响作用。
2.1 划分特征
在公交运行中,常根据不同的指标将公交服务过程划分为“高峰、平峰、低峰”三类,为验证如何行之有效地完成公交运营时段内的划分,通过对不同目标簇数目的设置,得到表3 的结果。
首先,随着目标簇数目的增加,公交运行时刻将划分的更为细致,研究人员可以根据期望的划分结果对簇数目进行设置。其次,无论目标簇数目为多少,设P= Ta-Tb/2N,簇中心时间标签间隔均大致为[P,2P,…,2P,P],边界点时间标签间隔大致为呈现明显的规律性分布。这是因为各个元素在时间上分布较均匀所导致的。而若改变时间标签基本单元为Xmin,将对时间标签分布规律没有影响。这是由于若使用欧式距离与作为目标函数,虽然在计算过程中横坐标差值大小发生变化,但元素与各簇中心的相对距离仍然不变,元素划分至簇的结果不造成影响,只要保证数据分布形式不变将不会改变该时间标签分布规律。
2.2 计算复杂度
经典的K-means 算法中,若从大小为m的元素集合中选取K个簇中心,每个元素为n维,共迭代I次,则完成一次计算的时间复杂度为
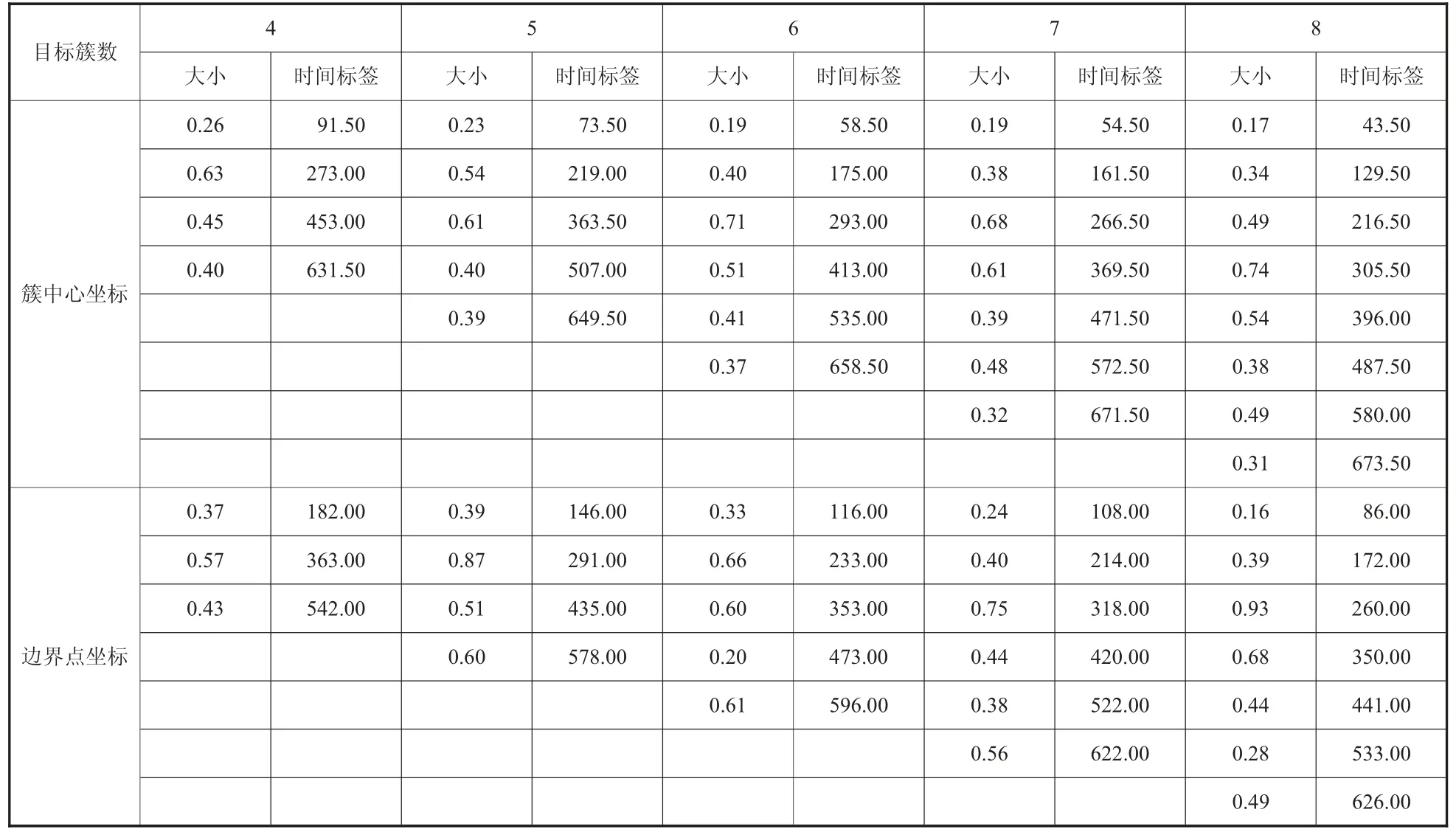
表3 不同簇数目划分结果表
在簇中心随机生成且目标簇数为K的条件下,多次进行计算时初始簇中心将出现K! 种分布情况。若簇中心集中多次出现,则簇中心迭代过程将需要额外进行多次计算复杂度为)的运算。在大规模样本数据下,若使用本文簇中心等间距平均生成的改进规则1,将节省上述的计算时间。
每次计算各元素与簇中心距离需要m·n·K次运算,根据本文基于时间标签的改进运算规则2,每个元素有1/K的概率位于与簇中心Ci最近,其中i的数学期望为K/2,则该运算过程数学期望为:
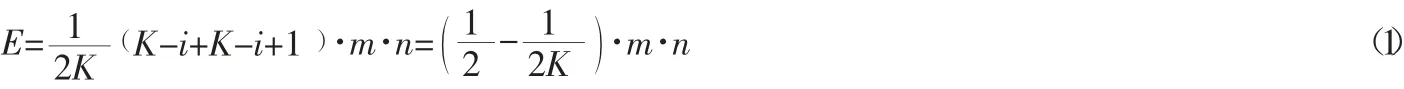
对于波动性较强的公交运行而言,难免会出现极端值的出现。不同于常规的剔除操作,改进运算规则3 虽然每个元素会带来O(m·n·)
n的运算复杂度,但仍在多项式时间内可完成计算。与此同时,通过隶属概率保留该类数据,结合对边界数据的处理将使时段划分结果更具有可靠性。
3 研究结论
本文针对公交时段划分问题,提出了基于K-means 聚类的划分方法。针对GPS 数据规模大,传统K-means 计算过程需较长时间的问题,从初始簇中心生成、元素归类计算及边界元素的归属上提出基于GPS 时间标签的运算优化规则。
以昆明市5 路公交车辆运行GPS 数据为例验证了方法的可行性,同时讨论了使用该方法进行公交运行时段划分时簇中心与边界元素时间标签的分布特征,并给出了算法上的解释。最后,讨论了提出改进规则前后在计算复杂度上的变化,为公交运营时段划分工作快速准确地完成提供了新的思路。
